Epilogue

드디어 대망의 마지막 장입니다. 이번 장에서는 지금까지 배웠던 기계학습을 정리하고 강의에서 다루지 못했던 기계학습에 대해 간략하게 설명하고 마무리합니다.

Outline

이번 장은 크게 4가지의 소주제로 이루어져 있습니다. 가장 먼저 지금까지 배운 기계학습을 간단하게 정리하고, 본 강의에서 다루지 못했던 기계학습 중 Baysian Learning과 Aggregation Methods를 간략하게 소개합니다. 마지막으로는 강의에 큰 도움을 줬던 분들에게 감사를 표한다고 합니다.

The Map of machine learning

기계학습을 다루는 책들은 굉장히 많은 내용을 소개하고 있습니다. 이것들 중 일부분을 나열하면 위와 같이 정신이 없을 정도로 많은 주제가 있음을 알 수 있습니다. 어떤 것들이 있는지 대충 보시면 지금까지 다루었던 것들도 있지만, 그렇지 않은 것들도 있다는 것을 아실 겁니다.

이렇게 보기 힘들게 주제들을 나열하면 머리만 아프고 이해도 힘드니, 강의에서는 좀 더 체계적인 방법으로 기계학습을 분류한 것을 보여줍니다.

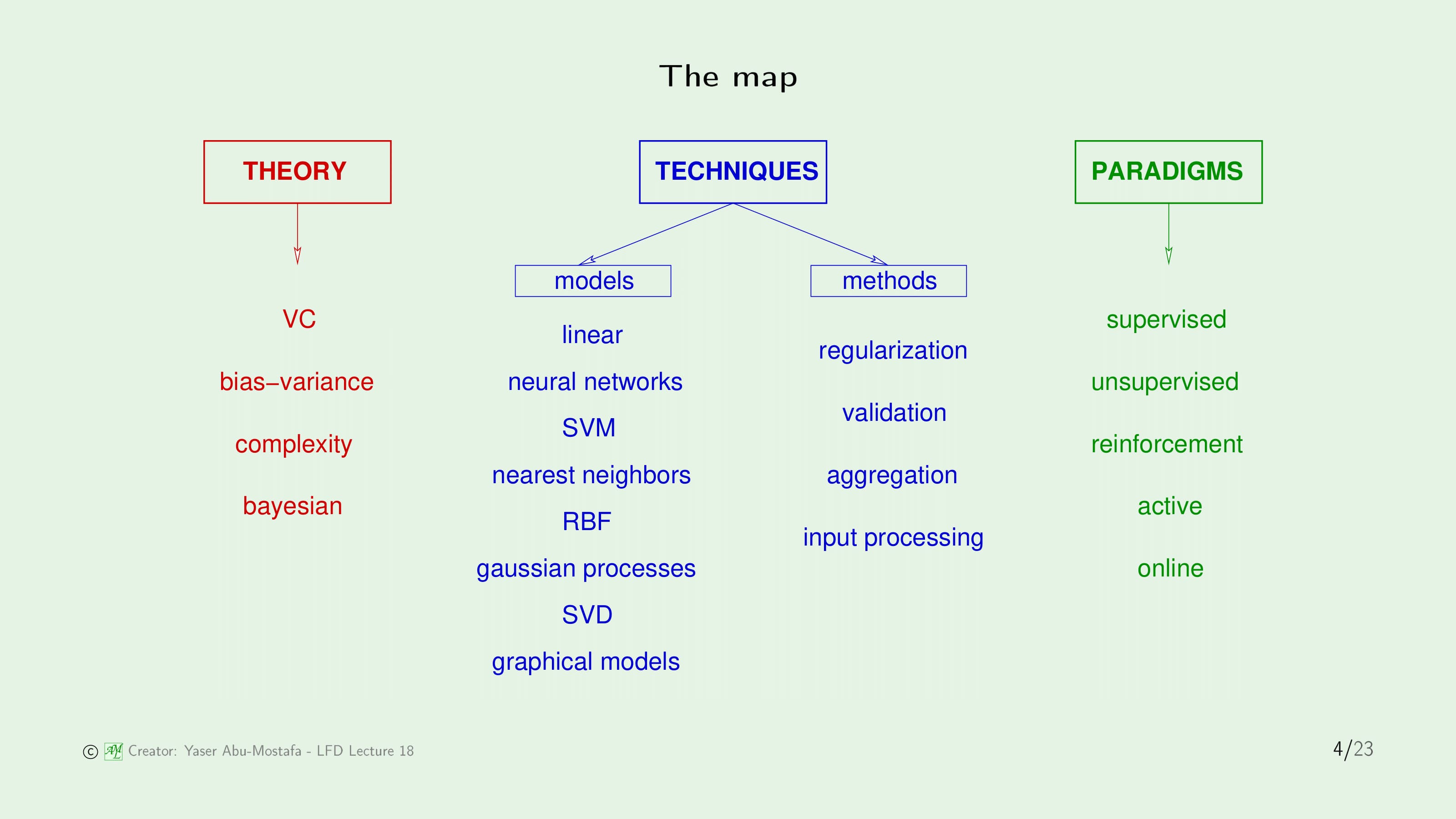
먼저 기계학습의 분야에는 크게 3가지 갈래가 있습니다. 첫째는 Theory (이론), 두 번째는 Technique (기술), 마지막으로 Paradigm (패러다임)이 있습니다. Paradigm은 학습 상황에 대한 다른 가정을 의미합니다. 수학적 가정이 아니라 Supervised Learning이나 Reinforcement Learning과 같은 다른 학습 상황을 다루는 가정이라는 뜻입니다. 이러한 가정을 할 때, 해결해야 할 문제는 기존의 기계학습의 문제와 다르기 때문에 공부해야 할 지식이 달라지게 됩니다. 그렇기에 이것을 Paradigm이라고 부릅니다.

가장 상위 개념인 Pradigm부터 이야기하면, Supervised Learning은 본 강의 대부분에서 다루는 주제였습니다. PLA부터 Support Vector Machine까지 대부분의 학습 알고리즘은 데이터에 Label이 있는 상황을 가정한 것이었기 때문입니다. 기계학습에서 가장 인기 있으면서도 유용한 주제입니다. Unsupervised Learning은 본 강의에서 많이 다루지는 않았지만, 최소한 Clustering이라는 핵심 아이디어를 배웠습니다. Reinforcement Learning은 첫 번째 강의에서만 잠깐 언급하였습니다. 좋은 행동을 하면 보상을 주고(강화하고) 나쁜 행동에 패널티를 부과하여 결국에는 좋은 해결책으로 수렴하게 만드는 방법입니다. 그 외에 Active Learning이나 Online Learning 등이 있지만 강의에서는 다루지 않았기에 생략하겠습니다.

다음으로 Theory 입니다. 기계학습에서 주요 이론은 Vapnic-Chervonenkis (VC) 이론입니다. 7장부터 시작하여 이후로도 지속적으로 기계학습의 일반화를 설명하기 위해 VC, 그리고 Bias-Variance 이론을 다루었습니다. Complextiy는 기계학습에서의 실용적인 부분입니다. 강의에서는 다루지 않았지만, 이것이 다항시간 내에 일어나는지, 혹은 그렇지 않은지를 통해 이론적인 알고리즘을 실질적으로 구현이 가능하지를 분석하는 이론입니다. 마지막으로 Bayesian은 기계학습을 확률의 한 갈래로 취급하는 이론입니다.

마지막으로 Technique은 Model과 Method 2가지로 분리됩니다. Model은 지금까지 대부분의 강의에서 다루었던 부분입니다. 기본적인 Linear Model부터 시작하여 선형 분리가 되지 않는 데이터 집합에서 어떻게 처리해야하는지 Transform과 Neural Network 등을 배워나갔습니다. 그 이후로도 SVM, RBF를 포함하여 많은 영역을 다루었습니다. 이 외에도 Gaussian Process, Singular Value Decomposition (SVD), Graphical Model 등이 있지만, 강의에서 이 모든 것을 다루지는 못했습니다.

Method는 Model에 관계없이 많은 영역을 다루기 때문에 매우 중요합니다. 강의에서는 Neural Network를 기점으로 발생할 수 있는 위험성인 Overfitting을 해결하기 위해 이 부분에 많은 시간을 투자하였습니다. Regularization과 Validation이 바로 대표적인 해결 방법이었습니다. Aggregation과 Input Processing은 강의에서 다루지 않은 요소입니다. 그중 Input Processing은 기계학습의 실무 과정에서 많이 다루는 실용적인 방법입니다.

이번 장의 나머지 부분은 지금까지 나열했던 것 중 Bayesian과 Aggregation에 대해 다룰 예정입니다.

Bayesian learning

먼저 Bayesian Learning으로 넘어갑니다. 깊이있게 이 내용을 다루기보단, Bayesian 접근법의 기초를 다룰 것이며 언제 사용할 수 있는지, 단점은 무엇인지 정도만 짚을 것입니다.

오랜만에 Learning Diagram을 살펴봅시다. 이 Diagram에서 확률적인 요소는 두 가지가 있었습니다. 하나는 Data가 알 수 없는 특정한 확률분포에 의해 생성된다는 것이었고, 다른 하나는 Input $\mathbf{x}$가 주어졌을 때 Output $y$가 나올 확률이었습니다. 이것은 Noise로 인해 더 이상 Target Function이 아니라 Target Distribution으로 불리게 되었기 때문이었습니다,

Bayesian 접근 방식은 이러한 확률적인 역할을 확장하는 개념입니다. 이전에 9장에서 Likelihood (가능도)를 잠시 떠올려보면, 가설 $h$와 Target Function $f$가 같다면 $\mathcal{D}$가 주어졌을 때 Output $y$를 얻을 확률을 의미하였습니다. 그래서 주어진 데이터를 제일 잘 표현할 수 있는 최대 확률을 계산하였습니다.

Bayesian 접근 방식은 이와 반대로 접근하고 있습니다. 데이터가 이미 발생하였기 때문에, 수 많은 가설 중 Target Function을 가장 잘 반영하는 가설이 무엇인지를 찾는 방법입니다.

Bayesian 접근 방식은 전공자들 사이에서도 의견이 분분합니다. 어떤 사람은 종교적인 수준으로 찬양을 하고, 어떤 사람은 완전히 쓰레기 같은 방법이라고 평가하기도 합니다. 강의에서도 이 점을 언급하며 Prior가 이러한 논쟁을 불러일으키는 주요 요소라고 합니다.

우리는 주어진 데이터 $\mathcal{D}$ 하에서 가설 $h$와 Target Function $f$가 일치하기를 바랍니다. 이것은 Bayes’ Theorem에 의해 가운데 식처럼 변형할 수 있습니다. 이 중 $P(\mathcal{D} \mid h=f)$는 로지스틱 회귀 등을 통해 구할 수 있습니다. 그리고 $P(h=f)$는 필요 없는 요소라고 하던데, 사실 제가 Bayesian을 잘 모르기 때문에 왜 그런지는 아직 모르겠습니다. 어쨌든 이 둘을 곱하면 Joint Probability Distribution을 얻을 수 있고, $P(h=f \mid \mathcal{D})$는 이것에 비례합니다.

Bayes’ Theorem에 나오는 항 중에 $P(h=f)$는 Prior라고 부르고 데이터를 얻기 전 가설 집합에 대한 믿음이라고 합니다. 이와 비슷하게 $P(h=f \mid \mathcal{D})$는 데이터를 얻은 후의 가설 집합에 대한 믿음이기 때문에 Posterior라고 합니다.

Bayes’ Theorem을 통해 만약에 Prior가 주어진다면, 전체 가설 집합에 대한 전체 확률 분포를 알 수 있습니다.

Prior의 예를 들어봅시다. 가설 $h$를 $d$차원 Perceptron 모델의 가중치 $\mathbf{w}$로 가정합니다.

가중치 $\mathbf{w}$의 Prior는 각각의 $w_i$가 독립적이고 $[-1, 1]$에서 균등하다고 정했다고 가정합니다. 이것은 모든 가중치에 대한 확률 분포를 얻을 수 있다면, 어떤 가중치가 특정 가설에 기여하는지 알 수 있음을 의미합니다.

하지만 Prior는 가정에 불과합니다. 아주 간단한 사례로 알 수 없는 숫자를 찾는 문제가 있다고 생각해봅시다. 내가 아는 정보는 그 숫자가 -1과 1 사이라는 것뿐입니다. 누군가가 이것을 -1과 1 사이의 Uniform Distribution으로 모델링하고 이것은 -1과 1 사이의 내가 모르는 숫자가 있다는 것과 동일하다라고 말한다면, 얼핏 듣기에는 그럴듯해 보이지만 그것은 틀린 사실입니다. 왜냐하면 Uniform Distribution에는 보이지 않는 많은 가정이 들어가 있기 때문입니다. 예를 들어 이 상황에서 많은 숫자를 뽑았을 때 Uniform Distribution의 평균은 0이지만, 원래 문제의 평균은 -1과 1 사이의 어떤 숫자이든 가능합니다. 실제로 이 문제와 동일한 것은 우리가 모르는 그 $x$가 $a$인 Delta Function으로 표현할 수 있습니다.

만약에 실제로 Prior를 알고 있다면, 모든 가설 $h$의 Posterior를 계산할 수 있기 때문에 완벽한 방법이 될 수 있습니다. 다시 말해, VC Analysis나 Regularization 같은 것도 필요 없이 가장 가능성 있는 가설을 선택할 수 있습니다. 심지어 모든 $\mathbf{x}$에 대해 가설의 평균 $\mathbb{E}(h(\mathbf{x}))$이나 Error Bar 또한 계산할 수 있습니다.

이 말은 예를 들어 주식 시장에서, 오늘의 주식 $\mathbf{x}$을 입력하면 가격 변동의 예상치나 그 예상치의 오차율까지도 계산이 가능하다는 말입니다. 상상할 수 있는 모든 것을 얻을 수 있다는 것입니다. 그렇기 때문에 정확한 Prior을 얻을 수 없다는 현실적인 문제로 인해, Bayesian 접근 방식을 선호하지 않는 과학자들도 있습니다. (사실 저도 이 방법은 좋아하지 않습니다)

Bayesian Learning이 올바르게 수행되기 위해선 둘 중 하나가 필요합니다. 첫째로, 유효한 Prior를 얻었을 경우에는 Bayesian Learning이 모든 다른 방법을 압도하는 해결방법이 됩니다.

둘째로, Prior가 무관하게 만드는 것입니다. Prior를 가정할 때 점점 더 많은 데이터를 얻고 Posterior를 보면, Posterior가 데이터 집합에 의해 크게 영향을 받고 Prior에 의해 점점 덜 영향을 받습니다. 그렇기 때문에 Prior가 중요하지 않은 데이터가 충분하다면, Prior를 개념적 요소가 아닌 것으로 생각할 수 있습니다. 이렇게 하면 유효한 Prior는 아니게 되지만, Prior를 가지고 데이터를 얻게 되면 Posterior 계산이 쉽습니다. 이것을 Conjugate Prior라고 하며, 전체 함수에 대해 Posterior를 다시 계산할 필요가 없습니다. 간단하게 말해, 계산 과정을 매개변수화하는 용도로만 Prior를 사용한다는 뜻입니다.

Aggregation methods

다음으로는 Aggregation Method입니다.

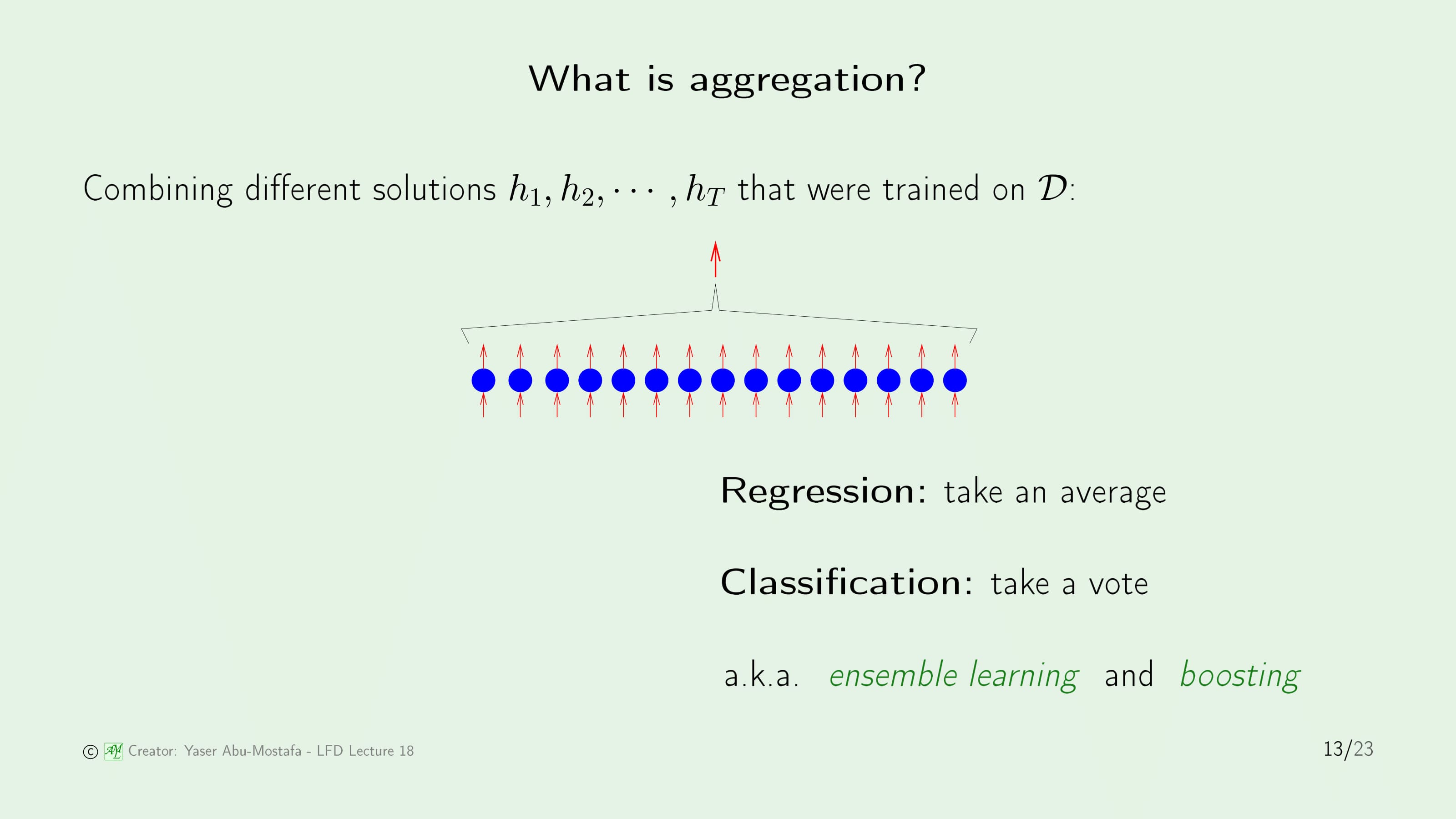
Aggregation은 모든 모델에 적용되는 방법입니다. 기본적인 아이디어는 다른 Solution을 결합한다는 것입니다. 예를 들어 컴퓨터 비전에서 사람의 얼굴을 구별하는 학습을 한다고 가정해봅시다. 여러 사용자에게 이 문제를 준다면 어떤 사람은 눈으로, 어떤 사람은 얼굴형으로, 어떤 사람은 이목구비의 위치로 사람을 구별할 것입니다. 총 관리자는 이들의 해결책을 결합해 최종적인 결과물을 만들 수 있을 것입니다.

그렇다면 결합하는 방법에 대해 이야기해봅시다. 의외로 방법은 간단합니다. 만약에 Regression 문제라면 그저 평균을 내면 되는 것이고, Classification 문제라면 더 많은 사람이 분류한 것으로 판단하면 됩니다.

아이디어만 보면 Aggregation과 2-Layer Learning이 비슷해 보입니다. 하지만 이 둘은 분명한 차이가 있습니다. 먼저 2-Layer Model은 모든 Unit이 동시에 참여합니다. 예를 들어 각 Unit에 Weight를 곱해서 더하는 방식으로 합치게 됩니다. 그에 반해 Aggregation은 각 Unit이 Training Data를 사용해 각자 학습하고, 각각의 Unit의 Output만을 사용해 최종 결과를 출력하는 방법입니다.

Aggregation에는 두 종류가 있습니다. 하나는 Aftter the fact 입니다. 이것은 이미 Solution이 있음을 의미합니다. 예를 들어 이전에 다루었던 Netflix 추천 문제는, 이미 기존의 여러 해결 방법이 존재했고 그것들을 합치는 것만을 고려하면 되었습니다.

다른 하나는 Before the fact 입니다. 이것은 결합하기 위한 Solution을 만드는 것입니다. 예를 들어, 주어진 데이터 집합 $\mathcal{D}$를 여러 번 독립적으로 Resampling (재생산)하여 모두에게 다른 Sample Data를 주는 것입니다. 그렇게 해서 각각의 Unit을 학습시키고 합치는 방법이 Before the fact가 됩니다.

Aggregation을 하기 위한 방법으로는 Boost Algorithm이 있습니다. 각각의 가설을 순차적으로 만드는 아이디어 입니다. 위 슬라이드에 나온 그림처럼 4번째 Unit을 만드는 상황에서, Training Data를 1~3번까지 만든 가설을 참고하는 것입니다. 이렇게 되면 각 Unit이 서로 관련이 생겨버리므로, 이를 독립시키는 과정이 필요합니다.

만약 몇 개의 Unit을 사용하여 Data를 60%는 올바르게, 40%는 틀리게 분류했다고 가정해봅시다. 그런데 다음 Unit에게 넘겨주는 데이터를 독립적으로 만들기 위해서 틀리게 분류한 데이터에 가중치를 부여합니다. 이 과정을 통해 올바른 결과와 틀린 분류를 50%/50% 비율로 맞춥니다. 이 방법을 사용한 가장 유명한 방법은 AdaBoost (Adaptive Boosting) 라고 합니다.

이번에는 이미 모든 Unit의 학습이 끝난 상태에서 결과를 합치는 Blending을 알아봅시다. Regression 문제에서 최종 가설 $g(\mathbf{x})$를 도출하기 위해서는 각각의 Unit들의 최종 가설인 $h_t(\mathbf{x})$에 가중치 $\alpha_t$를 곱한 다음 더해야 합니다.

가장 좋은 성능을 보이는 (=Error를 최소화하는) 결과를 내기 위해서는 적절한 $\alpha_t$를 정해야 합니다. Squared Error로 Measure한다고 가정한다면, Pseudo-Inverse를 통해 계산할 수 있습니다. 이 과정에서 특정 $\alpha_t$는 음수가 나올 수도 있습니다. 하지만 음수가 나왔다고 해당 가설이 Aggregation에서 쓸모가 없다는 뜻은 아닙니다. 가설이 Aggregation에서 쓸모가 있는지는 다른 방법을 통해 측정합니다.

어떤 가설 $h$가 Aggregation에서 얼마나 기여했는지 평가하는 방법은 그 가설 $h$를 포함했을 때의 결과와 포함하지 않았을 때의 결과를 비교하는 것입니다. 그 둘을 비교했을 때 Out of Sample Error의 차이가 크면 클수록 가설 $h$의 기여도가 높다고 판단할 수 있습니다.

Acknowledgements

이제 이론적인 내용은 모두 끝났고, 이 강의에 도움을 준 사람에게 감사를 표하는 시간입니다. (이 부분부터는 읽지 않으셔도 됩니다.)

가장 먼저 Malik Magdon-Ismail 교수님과 Hsuan-Tien Lin 교수님입니다. 이 두 교수님은 교재 작성에 큰 기여를 하셨고, 그 기여도로 인해 교재에도 공동 저자로 등록되어 있습니다.

다음으로 Carlos, Ron, Costis, 그리고 Doris는 강의 슬라이드 및 숙제 문제를 만드는데 큰 기여를 했다고 합니다. 특히 Carlos는 이 강의에서 Q & A 세션의 진행을 담당했고 마지막 온라인 강의에서 이 분의 얼굴을 볼 수 있습니다. Yaser 교수님이 이들이 받는 봉급보다 많은 일을 했다는 것으로 보아 이 4명은 대학원생인 것 같습니다.

Leslie와 Rich는 강의 중 슬라이드의 크기 등을 조절할 수 있게 도와주고, 강의를 촬영하여 온라인 강의를 제작할 수 있게 도움을 주었다고 합니다.

이 강의는 모든 사람에게 무료로 열려 있습니다. 하지만 그렇게 하기 위해 많은 돈이 필요했는데, 슬라이드에 나와있는 몇몇 Caltech의 직원들이 그 비용을 마련할 수 있도록 도와주었다고 합니다.

그 외에 언급하지 않은 모든 Caltech의 TA 및 스태프, 졸업생, 동문, 그리고 Yaser 교수님의 동료들로부터도 많은 도움을 받았다고 합니다.

마지막으로 가장 큰 가르침을 얻은 Faiza A. Ibrahim에게 감사를 표합니다. 가장 큰 글씨로 적었길래 누군가 하고 인터넷에 검색해보니 Yaser 교수님의 어머님이라고 나오네요.

이번 장에서는 각 슬라이드의 내용도 많고, 특히 제가 잘 모르는 분야에 대한 내용이 많아 정리하기 쉽지 않았습니다. 그렇기에 Yaser 교수님의 말씀을 최대한 오역하지 않도록 정리했는데, 나중에 다시 읽어보며 틀린 내용이나 어색한 표현을 찾아 고치겠습니다. 댓글로도 지적해주신다면 반영하도록 하겠습니다.

이로써 기계학습 관련 포스트는 여기까지입니다. 지금까지 읽어주셔서 감사합니다!