Neural Networks

10장은 인공신경망(Neural Network)에 대해 배우게 됩니다. 현재 인공신경망 모델은 기계학습의 대세가 되어 많은 관심을 받고 있습니다.

Outline

이번 장의 구성은 3개로 나뉘어 있습니다. 지난 장에서 배운 경사하강법(Gradient Descent)의 변형인 확률적 경사하강법(Stochastic Gradient Descent)를 배우고, 본격적인 인공신경망 모델에 대해서 배운 다음, 마지막으로 인공신경망 모델의 학습 알고리즘인 역전파(Backpropagation) 알고리즘을 배우게 됩니다.

Stochastic gradient descent

먼저 간단하게 지난 장에서 배운 경사하강법을 복습해보면, 처음에 무작위의 $w$를 정한 다음 기울기를 계산하여 어떤 방향으로 움직일 것인가를 정하여 $\mathbf{w}$를 단계적으로 값을 수정하여 In Sample Error가 최소가 되도록 만들어주는 방법이었습니다.

분명 경사하강법은 최적의 $\mathbf{w}$를 정하기 위한 좋은 방법이지만, 문제는 한 단계를 거칠 때마다 모든 데이터를 이용하여 방향을 결정해야 한다는 것입니다. 즉, 데이터의 개수가 $N$개라면, 매번 $N$개의 데이터의 $e(h(\mathbf{x}_n, y_n))$를 계산해야 한다는 것입니다. 데이터의 개수가 적다면 크게 문제 될 사항은 아니지만, 일반적으로 기계학습에서는 수많은 데이터를 보유하여 그것을 기반으로 문제를 해결하기 때문에, 계산량이 많다는 것은 결코 반가운 사항은 아닙니다.

이런 식으로 한번의 움직임을 위해 모든 데이터를 일괄적으로 처리하는 방식을 Batch 라고 합니다.

이 문제를 확률적으로 계산하기 위해 조금 다른 방법을 사용할 것입니다. 한 단계에서 오직 1개의 데이터 $(\mathbf{x}_{n}, y_{n})$ 만을 무작위로 추출하는 것입니다. 그리고 오직 그 1개의 데이터만을 사용해 경사하강법을 사용하는 것입니다.

언뜻 보면 전체의 데이터를 기준으로 방향을 정하던 때와 달리 한 개의 데이터만을 기준으로 방향을 정하기 때문에 원하는 결과가 나오지 않을 것이라고 생각이 들지만, 사실 이 방법은 이미 이전에 PLA에서도 사용한 방법입니다. 이런 방식으로 방향을 정하는 것이 일반적인 경사하강법과 같다는 것을 보이기 위해 “평균적인” 방향을 계산해보면, 경사하강법의 방향 계산 식과 동일하다는 것을 알 수 있습니다. 물론 하나하나의 단계에서는 경사하강법의 방향과 차이가 있을 수 있지만, 많은 횟수를 반복하게 되면 결과적으로는 원래의 경사하강법과 동일한 방향이 된다는 것입니다. 이 방법을 Stochastic Gradient Descent (확률적 경사하강법) 이라고 부릅니다.

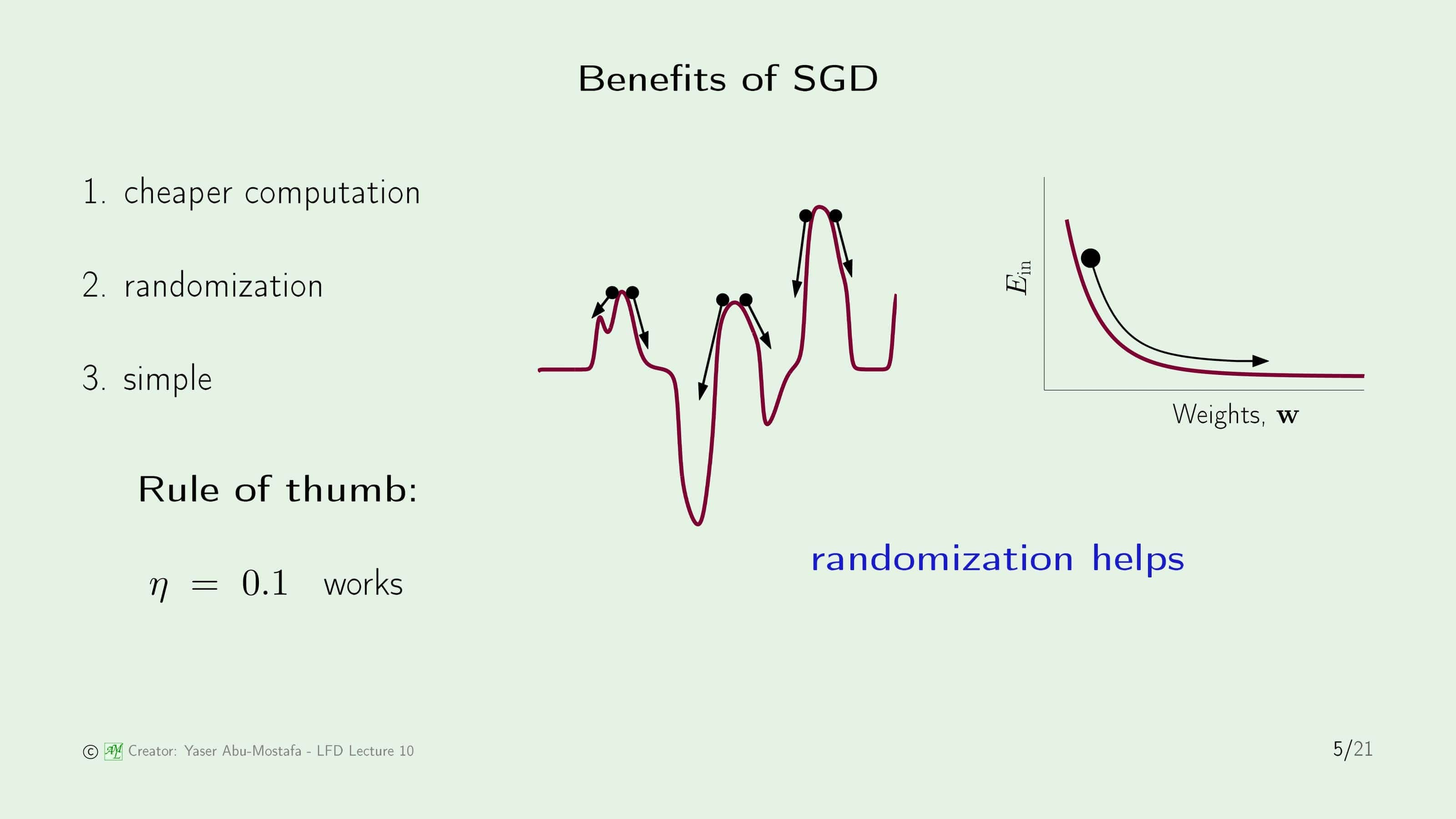
확률적 경사하강법의 장점으로는 먼저 경사하강법에 비해 계산이 빠르다는 것입니다. 두 번째 장점으로는 무작위성으로 인해 이득을 볼 수 있다는 것으로, 직관적으로 이해는 쉽지 않기 때문에 오른쪽 그림을 참고해봅시다. 지난 장에서 경사하강법을 설명했을 때 봤던 U자 모양의 그래프인 경우는 사실 일반적으로 잘 발생하지 않고, 보통은 중간의 그림처럼 울퉁불퉁한 모양의 그래프가 더 많이 발생합니다. 이런 울퉁불퉁한 모양의 그래프의 가장 큰 문제는, 전역 최솟값(Global Minimum)을 찾다가 지역 최솟값(Local Minimum)을 찾는 일이 발생한다는 것입니다. 그림상으로 봤을 때는 어느 부분이 지역 최솟값인지 쉽게 구분이 가능하지만, 실제 문제를 해결하는 과정에서는 그림이 아닌 수치로만 확인하기 때문에 지금 내가 찾은 답이 지역 최솟값인지, 전체 최솟값인지 구분이 되지 않는 문제가 있습니다. 만약에 방금처럼 무작위 하게 데이터를 선택하여 방향을 정한다면, (데이터가 고루 퍼져있다는 전제 하에) 지역 최솟값에 빠지더라도 그곳을 빠져나갈 수 있는 기회를 얻을 수 있습니다.

세 번째 장점으로는 간단하다는 것인데, 확률적 경사하강법의 경우 Learning Rate $\eta$를 보통 간단하게 0.1로 놓는다고 합니다.

1장에서 나왔던 영화 추천 문제를 다시 가져왔습니다. 유저의 영화 선호도는 코미디, 액션, 등장하는 배우 등으로 이루어진 벡터로 이루어져 있고, 영화 또한 영화의 장르, 등장하는 배우 등으로 이루어진 벡터가 있습니다. 이것을 이용하여 유저가 어떤 영화를 좋아할지 추천하는 시스템을 만들어야 하는데, 넷플릭스에서 기존의 방법보다 10% 향상시키는 방법에 대해 100만 달러의 상금을 걸었다고 언급했습니다. 이 예제가 왜 갑자기 이 곳에 다시 언급되었나 궁금했는데, 온라인 강의에서 확률적 경사하강법을 사용한 방법이 실제로 10%의 성능 향상을 이루어내 100만 달러의 상금을 탔다고 합니다.

100만 달러의 상금을 받은 방법을 간단하게 설명하자면, 유저와 영화의 각 요소를 곱한 값을 더해 영화에 매긴 평점과의 Squared Error를 계산한 것을 $\mathbf{e}_{ij}$로 놓고 확률적 경사하강법을 사용했다고 합니다. 방법 자체는 크게 어렵지 않아 보이지만, 마치 콜럼버스의 달걀처럼 보고 나면 쉬운데 막상 이걸 떠올리지는 쉽지 않았나 봅니다.

Neural network model

두 번째로 이번 장의 핵심인 인공신경망 모델에 대해 배워봅시다.

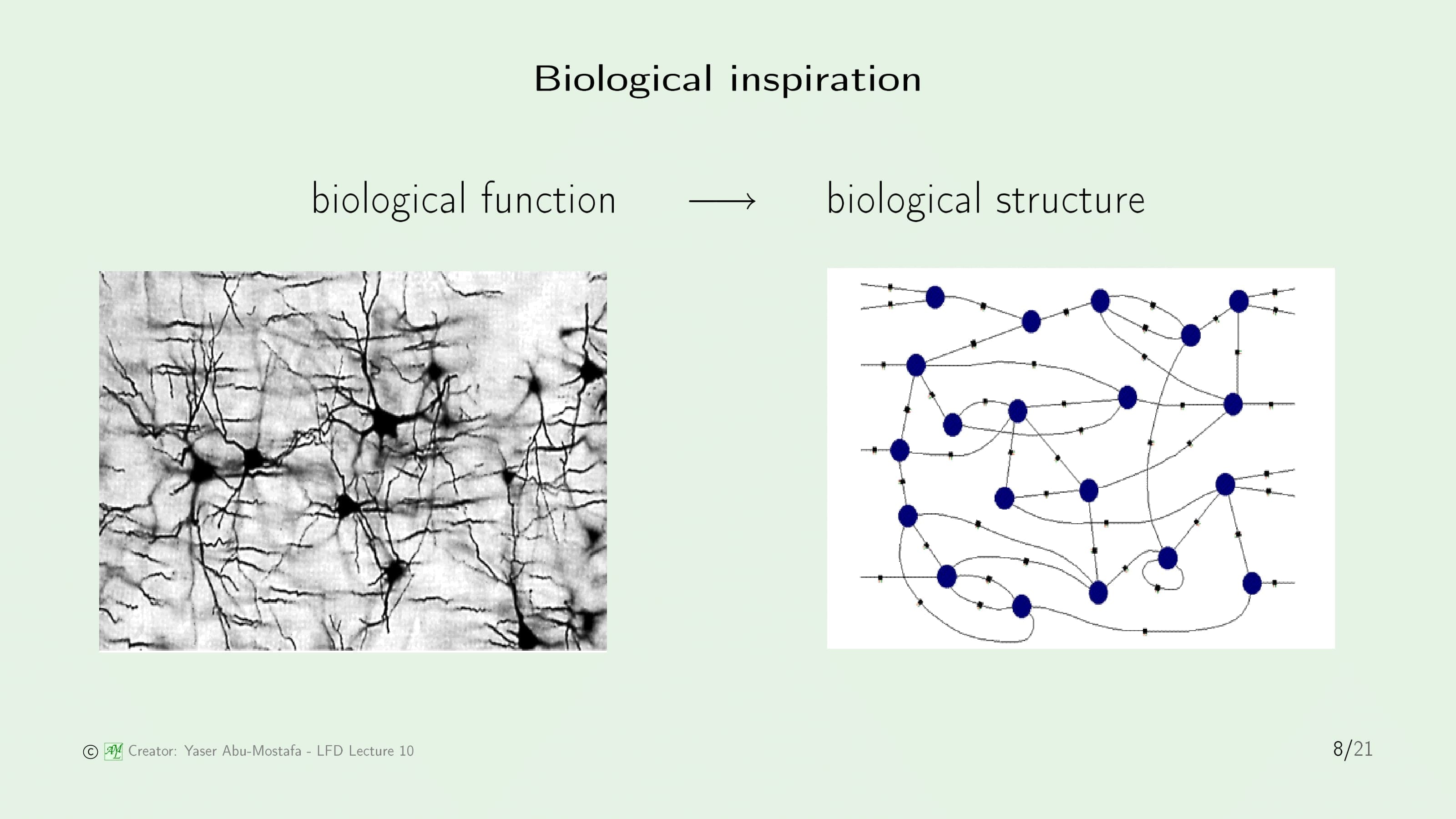
인공신경망은 이름에서 알 수 있듯이 신경망의 생물학적인 구조에서 영감을 얻어 만들어진 모델입니다. “배운다” 라는 생물학적인 기능을 구현하기 위해 생물학적인 구조를 모방한 것입니다. 물론 구조만 그렇게 만들고 끝나는 것이 아니라 생물학적으로 동작하게끔 유사한 시스템까지 구현해야 합니다.

신경망은 Synapse로 연결된 Neuron으로 구성되어 있습니다. 각 뉴런들은 입력을 받은 자극으로부터 간단한 연산을 한 후 그 결과를 내보냅니다. 마치, 퍼셉트론(Perceptron)과 유사하다고 생각하시면 됩니다. 인공신경망은 다수의 뉴런으로 구성되어 있는 신경망과 비슷하게 다수의 퍼셉트론으로 이루어져 있습니다.

1장에서 배운 퍼셉트론은 간단하고도 꽤 유용한 도구였지만, 지금까지 문제가 꾸준히 있었습니다. 특히 선형 분류가 되지 않은 문제를 해결하기 위해 여러 장에 걸쳐 꽤 많은 노력을 기울여왔습니다. 그러나 이런 노력에도 불구하고 퍼셉트론으로 아예 해결할 수 없는 문제도 있습니다. 위 슬라이드의 첫 번째 그림을 보면 +와 -가 서로 대각선 영역으로 나뉘어 있습니다. 이를 정확하게 나누기 위해서는 최소한 2개의 직선이 필요합니다. 그러나 퍼셉트론은 1개의 직선으로 이루어진 방법입니다. 따라서 기존의 퍼셉트론을 사용해서는 이 문제를 해결할 수 없는데, 만약에 이 문제를 두 번째와 세 번째 그림과 같이 $h_1, h_2$ 2개의 선으로 각각 나눈 다음 합칠 수는 없을까 라는 새로운 방법이 제시되었습니다.

두 개의 서로 다른 도구를 합치기 위한 방법은 기본적으로 OR 논리회로와 AND 논리회로인데, 슬라이드 아래의 그림은 이것을 퍼셉트론으로 구현한 것입니다. OR은 2개의 Input 모두 -1일 경우에만 Output이 -1이 나오고 그 외에는 모두 +1이 나오는 논리회로이고, AND는 2개의 Input 모두 1일 경우에만 Output이 1이 나오고 그 외에는 모두 -1이 나오는 논리회로입니다. 왼쪽 그림을 보시면 기본적으로 1.5의 값이 들어오기 때문에 $x_1, x_2$ 모두 -1이 들어와야만 -1이 나오고, 오른쪽 그림에서는 기본적으로 -1.5의 값이 들어오기 때문에 $x_1, x_2$ 모두 1이 들어와야만 1이 나오는 구조가 됩니다.

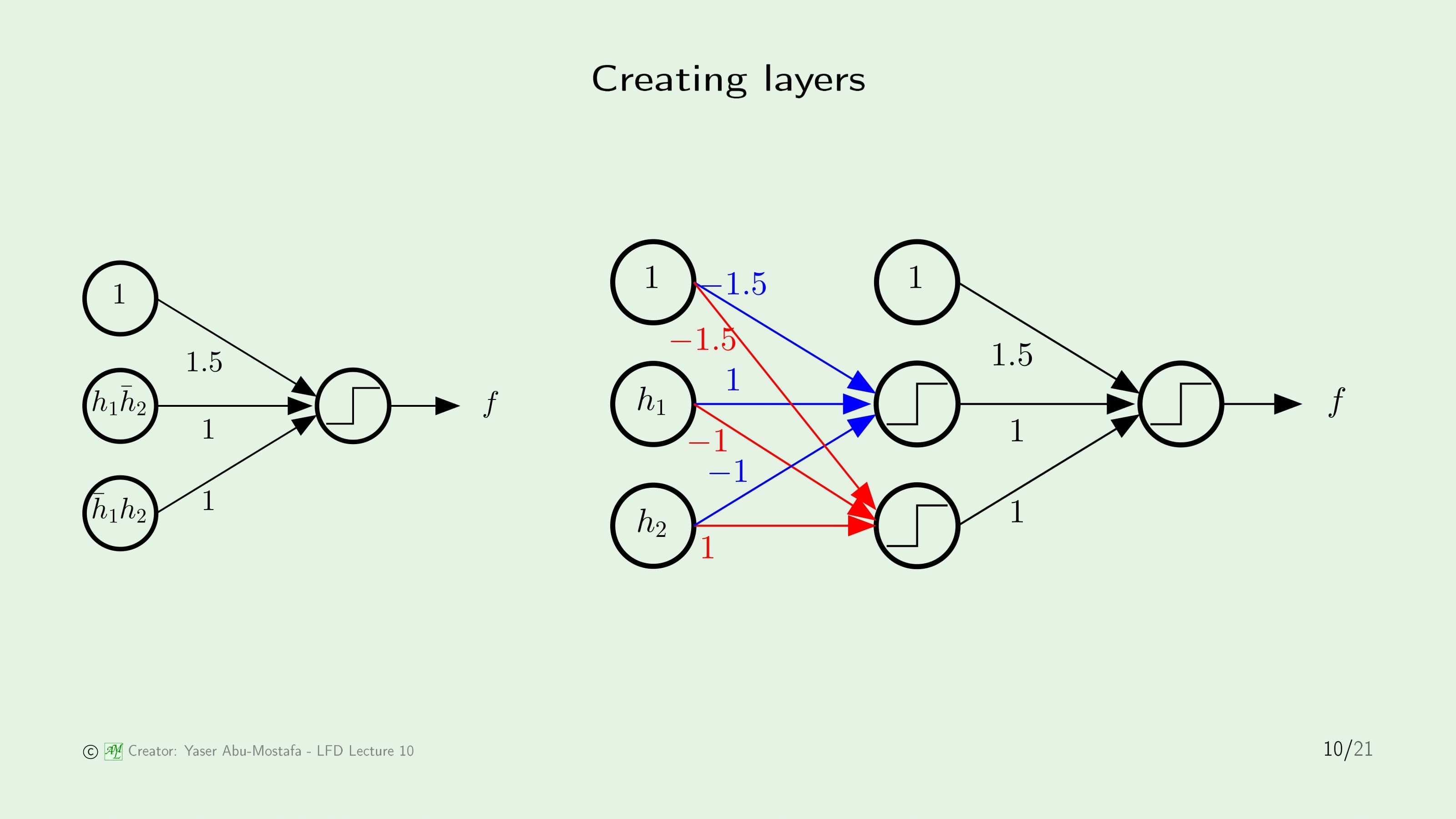
방금 배운 내용을 토대로, 위 슬라이드의 왼쪽 그림은 이전 슬라이드의 $h_1, h_2$를 가지고 이전 슬라이드의 위쪽 첫 번째 그림과 같은 분류가 되도록 논리회로를 구성한 결과입니다. Input이 조금 복잡한 모양을 가지고 있지만, 눈썰미가 좋으신 분은 XOR 논리회로를 구현한 퍼셉트론인 것을 아실 수 있을 것입니다. 이 표현방법이 틀린 것은 아니지만, Input이 너무 복잡하게 나와있기 때문에 $h_1, h_2$로만 Input이 구성될 수 있게끔 전개한 것이 위 슬라이드의 오른쪽 그림입니다.

오른쪽 그림에서 가장 왼쪽의 단계에서는 $h_{1}\bar{h}_{2}$와 $\bar{h}_{1}h_{2}$를 구현하였습니다. Threshold가 -1.5로 들어가고 있는 것을 보면 $h_1, h_2$의 입력을 각각 AND회로로 구성한 것을 알 수 있습니다. XOR를 구현하기 위해서는 $h_1$과 $h_2$가 서로 한번씩 NOT회로를 거쳐야 하는데, 오른쪽 그림에서는 그것을 구현하기 위해 가중치에 -1을 부여하는 것으로 해결하였습니다. 두번째 단계에서는 $h_{1}\bar{h}_2$와 $\bar{h}_{1}h_{2}$를 더하는 OR 논리회로를 구현함으로써 왼쪽의 그림과 동일한 Output이 나오도록 만들었습니다.

이전 슬라이드에서 문제에 맞게 그림을 수정하긴 했지만, 원래의 문제는 Input으로 $x_1, x_2$가 들어가지 $h_1, h_2$가 들어가는 게 아니었습니다. 따라서 $x_1, x_2$를 이용하여 $h_1, h_2$를 구현하는 것 또한 수행해 주어야 합니다. 퍼셉트론 $h_1, h_2$를 구현하기 위한 가중치 $\mathbf{w}_1$과 $\mathbf{w}_2$은 이미 구했다고 가정하고, 여기서는 그 구조만 표현하도록 합시다.

결과적으로 이 문제는 총 3단계를 거쳐 해결할 수 있게 되었습니다. 인공신경망에서 이 각각의 단계를 Layer라고 부릅니다. 또한 이 인공신경망의 구조는 Input에서 Output까지 다음 레이어로만 이동하고 이전 레이어로 돌아가지 않는데, 이러한 구조를 Feedforward 구조라고 합니다. 따라서 이 문제는 3개의 레이어로 구성된 피드포워드 인공신경망이라고 볼 수 있습니다.

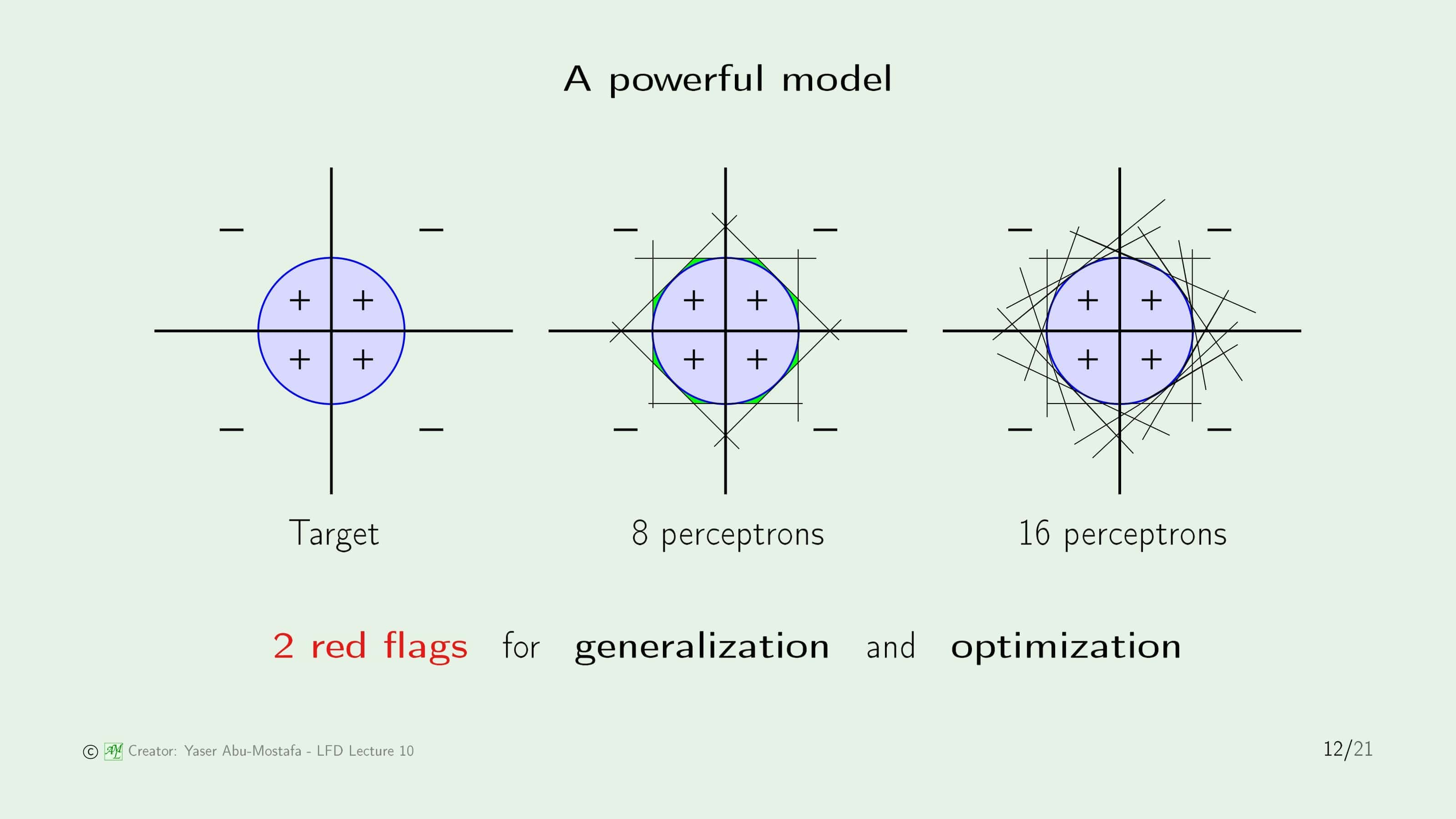
인공신경망 모델을 이용한다면 기존에 퍼셉트론으로는 해결할 수 없었던 많은 문제를 해결할 수 있습니다. 위 슬라이드의 첫 번째 그림은 퍼셉트론으로 풀 수 없는 예제입니다. 이전보다 조금 더 어려워 보이는 원(Circle)이 주어졌습니다. 직선으로 원을 표현하기는 힘드니 두 번째 그림처럼 8개의 퍼셉트론을 이용하여 8각형으로 처리하는 방법이 있습니다. 그러나 Target과 동일한 모양이 아니기 때문에 연두색 부분처럼 어느 정도의 오류가 발생하게 됩니다. 이 오류를 줄이기 위해 세 번째 그림처럼 8개의 퍼셉트론을 추가해 더 원에 가까운 16각형으로 처리할 수도 있습니다. 우리가 원한다면 더 많은 퍼셉트론을 이용해 최대한 원과 가까운 모양을 만들면서 오류를 줄여갈 수 있습니다.

그러나 이렇게 퍼셉트론을 많이 사용할수록 또 다른 문제가 생기게 됩니다. 많은 퍼셉트론을 사용할수록 필요한 가중치의 수와 자유도, VC Dimension이 늘어나므로 일반화가 어려워지게 됩니다. 이보다 더 큰 또 다른 문제는 모델이 복잡해질수록 최적의 가중치를 찾는 최적화까지 어려워진다는 것입니다.

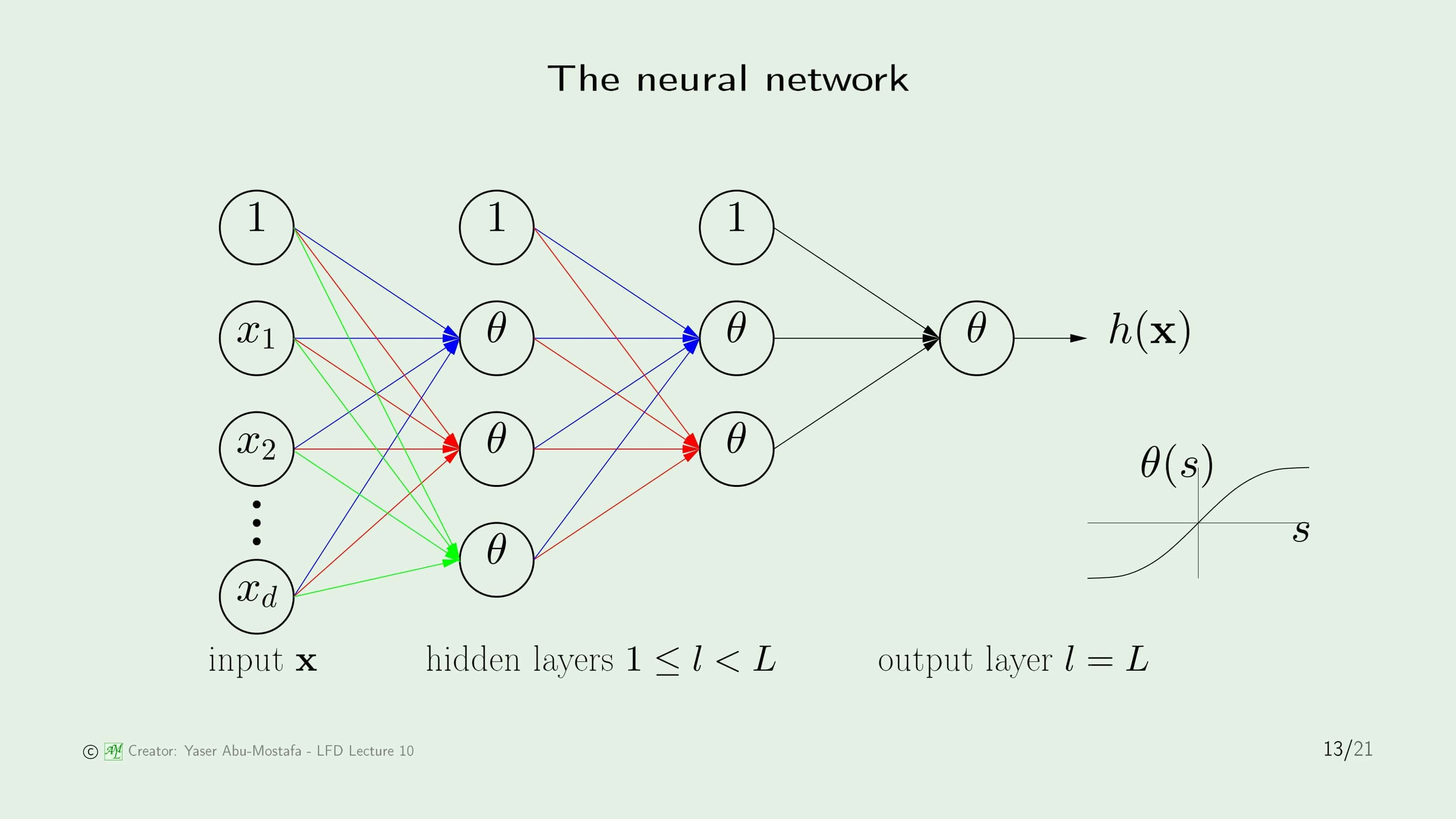
인공신경망의 일반적인 구조는 Input $\mathbf{x}$으로 이루어진 Input Layer, 그리고 로지스틱 함수 $\theta$로 이루어진 Hidden Layer, 결괏값을 내보내는 Output Layer로 이루어져 있습니다. 이 중 핵심은 Hidden Layer인데, 사용자가 일반적으로 어떤 값인지 알 수 없기 때문에 Hidden이란 이름이 붙었습니다.

그러나 인공신경망을 구현하기 위해서는 약간의 변형이 필요합니다. 이전 장에서 배운 로지스틱 함수는 ${e^s}/{(1+e^s)}$ 였지만, 이는 0과 1 사이의 값을 갖는 비선형 곡선이었습니다. 그러나 우리는 -1과 1 사이의 값을 갖는 것이 필요하므로, 함수를 조금 아래로 내려야 합니다. 로지스틱 함수는 입력이 0일 때 0.5의 값을 가졌으므로, 로지스틱 함수에 0.5를 빼주면 정확하게 원점을 지나게 됩니다.

\[\frac{e^s}{1+e^s}-\frac{1}{2}\]

문제는 이렇게 되면 함수의 크기상 -0.5와 0.5 사이만을 지나게 되는 문제가 있습니다. 우리가 원하는 것은 -1과 1 사이의 값을 갖는 것이니, 함수에 2를 곱해주어야 합니다.

\[2 \times \left( \frac{e^s}{1+e^s}-\frac{1}{2} \right)\]

이 식을 정리하면 우리가 많이 보던 쌍곡 탄젠트 함수($\tanh$)와 유사한 함수가 나오게 됩니다.

\[2 \times \left( \frac{e^s}{1+e^s}-\frac{1}{2} \right) = \frac{2e^s-e^s-1}{1+e^s} = \frac{e^s-1}{e^s+1}\]

입력만 $s$에서 $2s$로 바꾸어주면 쌍곡 탄젠트 함수 $\tanh$가 되는데, 왜 여기에 2를 곱해주는지는 사실 잘 모르겠습니다. 혹시 이 부분을 아시는 분은 댓글로 알려주시기 바랍니다.

인공신경망에서는 퍼셉트론에 비해 가중치의 수가 많이 늘어났기 때문에 이 가중치가 어디에 연결되어있는지 좀 더 정교한 표기가 필요합니다. 이제는 $w^{(l)}_{ij}$라는 방식으로 표기하는데, 이것은 레이어 $l$의 가중치 중 이전 레이어의 $i$번째 뉴런과 현재 레이어 $l$의 $j$번째 뉴런이 연결되어있다는 뜻입니다.

또한 입력에 대한 표기법도 정교해졌는데, 이전 레이어의 Output이 다음 레이어의 Input이 되기 때문입니다. 입력의 표기는 $x^{(l)}_j$로 하는데, 이것은 레이어 $l$의 $j$번째 뉴런의 Input이라는 뜻입니다.

Backpropagation algorithm

이제 인공신경망에서 각각의 가중치를 학습하기 위해 사용하는 Backpropagation Algorithm (역전파 알고리즘)을 배워봅시다.

기본적으로는 이번 장 앞부분에서 배운 확률적 경사하강법을 사용합니다. 모든 가중치 $\mathbf{w}$를 학습할 때 한번에 1개의 데이터 $(\mathbf{x}_n, y_n)$을 사용하는데, 이 때의 오류를 $\mathbf{e}(\mathbf{w})$로 정의합니다. 확률적 경사하강법을 구현하기 위해서는 $\mathbf{e}(\mathbf{w})$의 기울기를 구해야 하는데, 모든 가중치의 값을 변화시켜야 하므로 모든 레이어 $l$, 모든 $i$, $j$를 잇는 뉴런에 대해서 수행해야 합니다.

문제를 간단하게 접근하기 위해 $\nabla\mathbf{e}(\mathbf{w})$를 차근차근 분석해봅시다. 이 강의에서는 효율적인 계산을 위해 연쇄 법칙(Chain Rule)을 사용하였습니다. 오류와 가중치 간의 직접적인 기울기를 계산하는 것이 어렵기 때문에 오류 $\mathbf{e}(\mathbf{w})$와 로지스틱 함수를 거치기 전의 값인 $s^{(l)}_j$, $s^{(l)}_j$와 가중치 $w^{(l)}_{ij}$의 기울기를 각각 계산하는 방법을 이용합니다.

연쇄 법칙을 이용하게 되면 문제가 약간 간단해집니다. 일단, 입력 $x^{(l-1)}_i$와 가중치 $w^{(l)}_{ij}$를 곱한 것이 $s^{(l)}_j$이므로, $s^{(l)}_j$를 $w^{(l)}_{ij}$로 편미분하게 되면 $x^{(l-1)}_i$만 남기 때문입니다. 아쉽게도 오류 $\mathbf{e}(\mathbf{w})$를 $s^{(l)}_j$로 편미분한 것은 간단하게 정리하지 못하지만, 표기만이라도 간단히 하기 위해 이를 $\delta^{(l)}_j$로 정의합니다.

지금까지 경사하강법에서 가중치를 계산할 때는 출력을 기준으로 계산했기 때문에, 이번에도 최종 출력인 마지막 레이어에서 먼저 $\delta^{(l)}_j$를 계산해봅시다. 마지막 레이어 $L$은 출력을 위해 단 1개의 뉴런만 존재하므로 $j$는 1이 됩니다. 이곳에서 $\mathbf{e}(\mathbf{w})$는 $\mathbf{e}(x^{(L)}_1, y_n)$이고, 이를 풀어쓰면 $(x^{(L)}_1 - y_n)^2$가 됩니다. $x^{(L)}_1$은 $s^{(L)}_1$가 쌍곡 탄젠트 함수 $\theta$를 거친 값이므로 최종적으로 $\theta$의 미분값을 계산하게 되면 $1-\theta^2(s)$가 됩니다.

마지막 레이어에서의 $\delta$를 계산했으니, 이제는 그보다 이전 레이어의 $\delta$를 구하기 위해 두 $\delta$간의 관계를 찾아보도록 하겠습니다. 이번에도 계산에는 연쇄 법칙을 사용하는데, 이전보다는 조금 더 복잡하게 2번을 사용하게 됩니다. 두 번째 단계에서 시그마가 갑자기 튀어나오는 것이 이해가 안 가실 수도 있는데, 다변수함수에서 편미분을 하게 되면 아래처럼 시그마가 나오게 됩니다.

\[\frac{\partial}{\partial t}f(x_1, x_2, \ldots, x_N) = \sum_{i=1}^{N}\frac{\partial f}{\partial x_i} \times \frac{\partial x_i}{\partial t}\]

이렇게 연쇄 법칙으로 3덩이로 식을 나누게 되면, 각각의 덩이를 간단하게 표현할 수 있으므로 문제가 간단해집니다. 최종적으로는 맨 아래의 식과 같이 이전 레이어의 $\delta^{(l-1)}_i$와 이후 레이어의 $\delta^{(l)}_j$ 사이의 관계를 찾았으므로, 첫 번째 레이어의 $\delta$부터 마지막 레이어의 $\delta$까지 모두 계산할 수 있게 됩니다.

지금까지 배운 내용을 알고리즘으로 정리하였습니다. 하나 특이한 점은, 가중치의 갱신을 위해서는 마지막 레이어부터 맨 앞의 레이어까지 반대방향(Backward)으로 계산하지만, 마지막 레이어에서 오류를 계산하기 위해서는 주어진 가중치로 첫번째 레이어부터 마지막 레이어까지 정방향(Forward)으로 계산해야 한다는 것입니다. 즉, 매 단계에서 앞으로 한번 계산하고, 뒤로 한번 계산하는 과정을 거쳐야만 합니다.

마지막으로 이전에 배운 비선형 변환(Nonlinear Transform)과 인공신경망 모델과는 어떤 차이가 있는지 알아봅시다. 비선형 변환과 인공신경망 모델 모두 선형 분리가 되지 않는 데이터를 제대로 분리하기 위한 방법입니다. 차이가 있다면 비선형 변환의 경우 직접 특정한 함수를 찾아 데이터를 다른 차원으로 변환하였지만, 인공신경망 모델에서는 가중치를 학습시킴으로써 데이터를 분류하는 것이므로, 학습된 비선형 변환으로 부르기도 합니다.

그렇다면 제대로 학습하기 위해 히든 레이어의 수나 뉴런의 수는 어떻게 조정해야 할까요? 그 문제는 다음 장에서 다루게 됩니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.