Radial Basis Functions

16장은 Radial Basis Function을 배우게 됩니다. 이것으로 데이터에 Label이 없는 Unsupervised Learning을 해결하는 방법을 배우게 됩니다.

Outline

이번 장에서 다룰 내용은 총 4가지인데, 첫 번째 주제를 제외한 나머지는 짧게 다루기 때문에 분량은 다른 장들과 비슷합니다. 첫 번째로 Radial Basis Function 표준 모델을 배우고 Nearest Neighbors Algorithm과 비교합니다. 두 번째로는 Neural Network와 간단하게 비교, 세 번째로 RBF와 Kernel Method와의 비교, 그리고 마지막으로 Regularization과의 비교를 다룰 것입니다. 여기서의 비교는 서로의 연관성과 차이점을 찾는 것입니다.

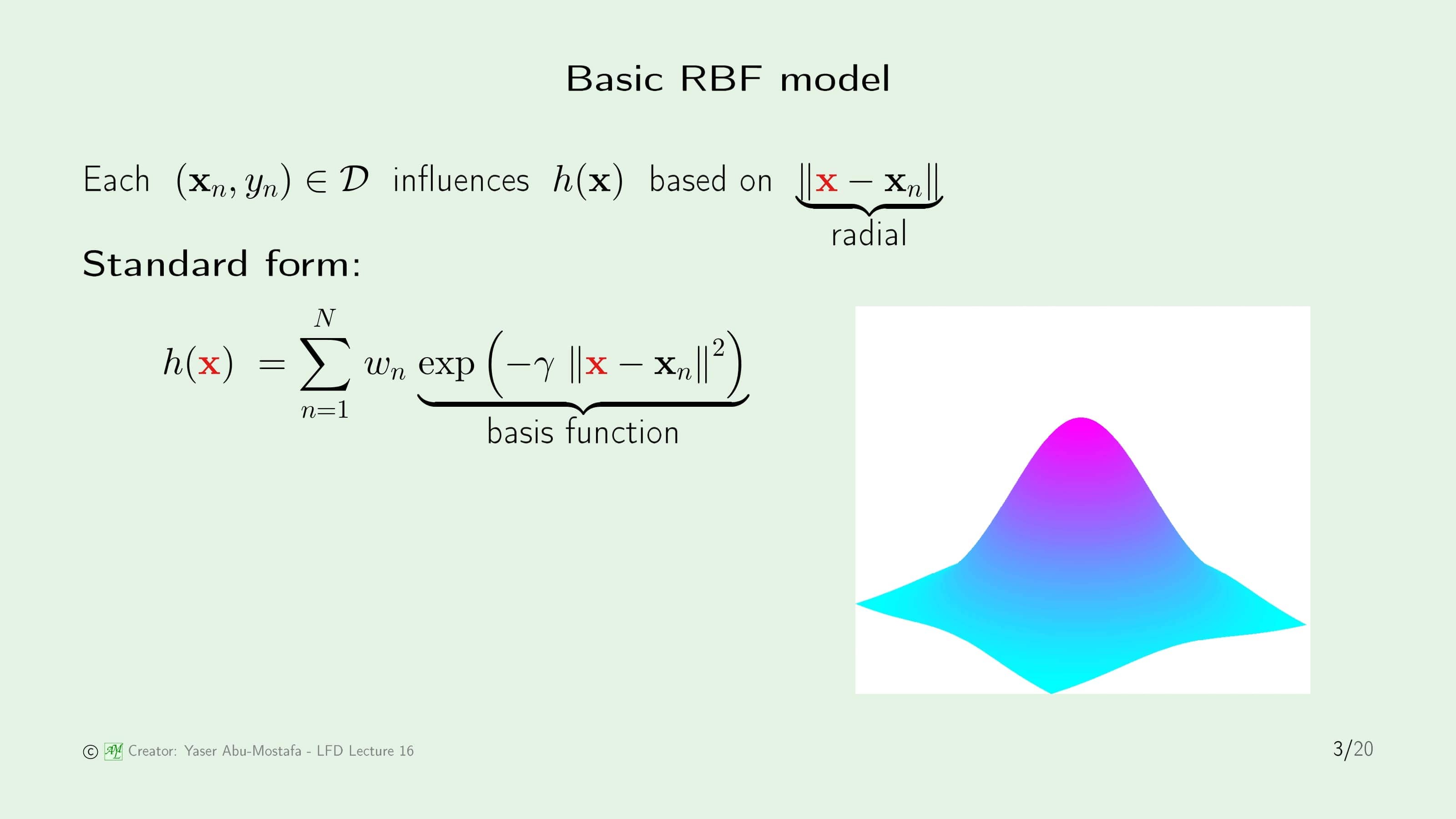
Radial Basis Function의 기본 아이디어는 데이터 집합의 모든 점이 가설에 영향을 준다는 것입니다. 그런데 잠깐 생각해보면 데이터 집합을 통해 가설을 만들기 때문에 데이터 집합이 가설에 영향을 주는 것은 당연한 것이 아니냐고 생각할 수 있습니다. 하지만 RBF는 ‘거리’라는 특별한 방법으로 영향을 받습니다. 다시 말해, 데이터 집합의 한 점이 근처에 있는 다른 점에 영향을 미친다는 것입니다.

이해를 돕기 위해, 슬라이드 오른쪽에 나와있는 산 모양의 그림을 봅시다. 산 꼭대기에 데이터 집합 중 한 점 $\mathbf{x}_n$이 있다고 가정해보면, 이 그림은 $\mathbf{x}_n$이 이웃에 대한 영향력이 크다는 것을 나타내고 있습니다. RBF는 거리에 비례하기 때문에, 이 그림은 모든 방향에 대해 대칭적인 구조라는 것을 알 수 있습니다.

RBF의 기본 형태는 복잡해보이지만, 구조를 이해한다면 생각보다 간단한 개념임을 알 수 있습니다. 먼저 데이터 집합 중 임의의 데이터 점 하나를 $\mathbf{x}$로 정합니다. 가설은 이 점을 기반해서 도출되기 때문에, $h(\mathbf{x})$라고 부릅니다.

그다음 다른 모든 데이터가 이 $\mathbf{x}$와 얼마나 떨어져 있는지를 계산합니다. 여기서는 Gaussian Function을 사용합니다. 이것이 $\text{exp}( \cdot )$ 부분입니다. 그런 후 데이터 집합의 각 점 $\mathbf{x}_n$이 얼마나 중요한지를 나타내는 가중치 $w_n$이 붙습니다. 나중에 다시 나오겠지만, 이 가중치 $w_n$은 $y_n$과 관련이 있습니다.

이 과정을 $N$개의 모든 데이터에 수행해주면 RBF 표준 모델 $h(\mathbf{x})$을 만들 수 있습니다. 이것이 Radial Basis Function이라고 부르는 이유는 $\lVert \mathbf{x} - \mathbf{x}_n \rVert$이 Radial Function이고, $\text{exp}( \cdot )$이 Basis Function이기 때문입니다.

모델을 알았으니, 이제 RBF의 학습 알고리즘이 무엇인지 알아봅시다. RBF의 기본 형태를 보시면 데이터 집합은 이미 주어졌으니 가중치 $w$만 구하면 됩니다. 그런데 기본 형태를 보시면 가중치의 개수는 $N$개이고, 데이터를 하나하나 대입해서 나오는 식 또한 $N$개입니다. 고등학교 수학에서 미지수의 개수와 식의 개수가 같으면 정확히 1개의 해답이 나오는 것을 배웠습니다. 그렇기 때문에 모든 가중치 $w$를 구하게 되면 In Sample Error가 정확히 0이 됩니다.

이전 슬라이드에서 보았듯이 학습 알고리즘은 매우 간단합니다. 결과적으로 이 문제는 $N$개의 방정식이 주어지고 $N$개의 미지수를 구하는 산수 문제이기 때문입니다. 다만 미지수의 개수가와 방정식의 수가 주어진 데이터의 수와 같기 때문에 그것이 매우 귀찮은 일일 뿐입니다.

그렇기 때문에 여기서는 행렬을 사용해서 미지수를 한번에 계산합니다. 선형대수학에서 방정식의 미지수를 구할 때 역행렬을 사용해 계산하는 방법을 배웠으므로 그 방법을 사용하면 간단하게 모든 가중치를 구할 수 있습니다. 이것을 Exact Interpolation (정확한 보간)이라고 부릅니다.

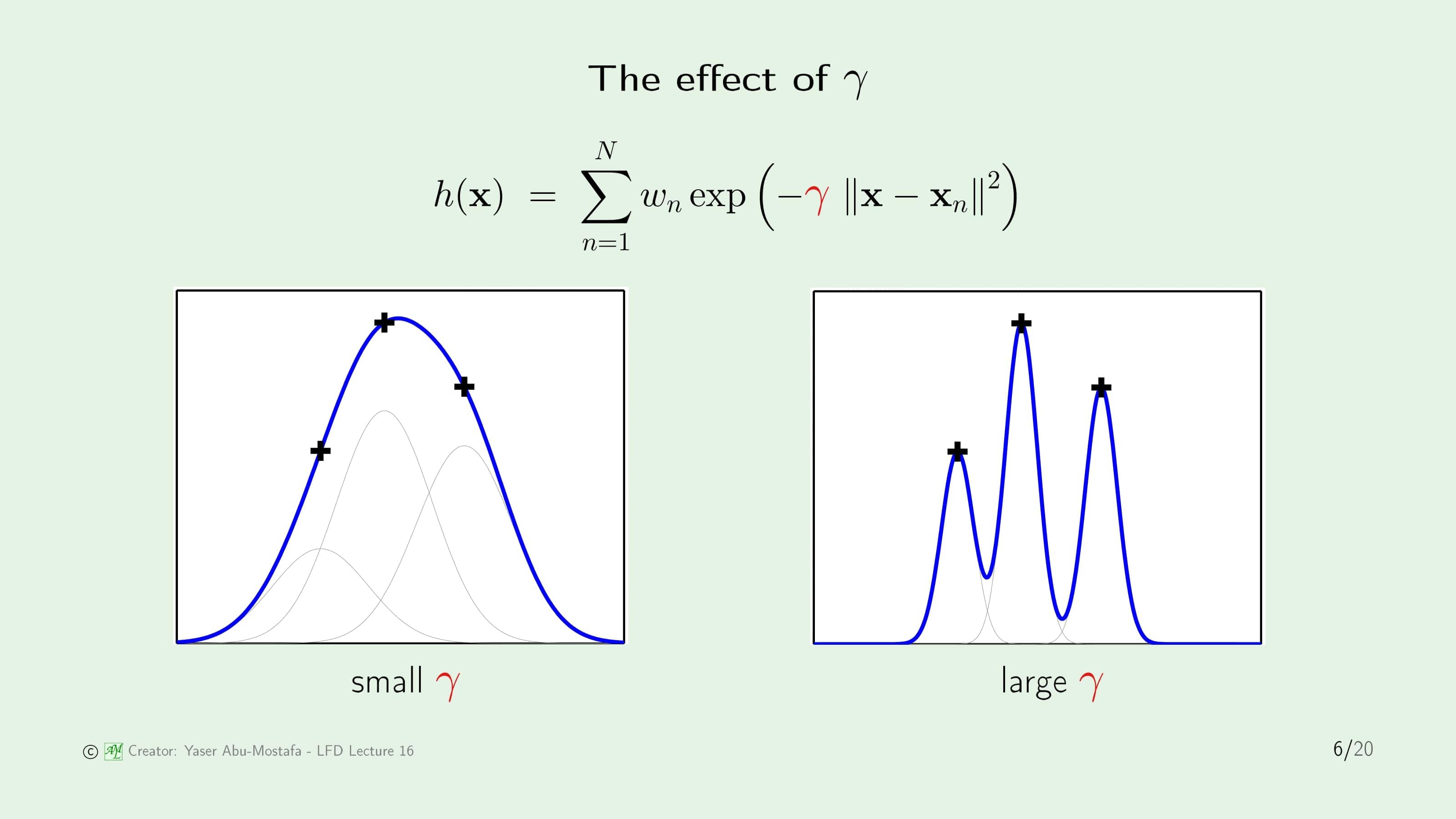
이제 RBF에서 $\gamma$의 값이 어떻게 영향을 주는지 알아봅시다. 먼저 $\gamma$의 값이 작다고 가정해봅시다. Gaussian Distribution (정규분포)의 그래프를 생각해보시면 비교적 분포가 고른 완만한 모양이 될 것입니다. 반대로 $\gamma$의 값이 크다면 평균에 대부분이 몰려있는 모양이 됩니다. RBF에서는 이러한 Gaussian Function의 합으로 이루어져 있기 때문에 $\gamma$의 값에 따라 어떤 모양이 될지 대략적으로 상상할 수 있습니다.

예를 들어, 데이터 집합이 단 3개의 점으로 이루어져 있다고 가정해봅시다. $\gamma$의 값이 큰 경우에는 각각의 데이터 점에 몰려있는 Gaussian Function의 합이기 때문에 데이터 점에서 조금만 거리가 멀어져도 그 영향력이 확 줄어버리게 됩니다. 결과적으로 오른쪽 그림처럼 뾰족뾰족한 모양이 됩니다.

이번에는 $\gamma$의 값이 작다고 가정해봅시다. 이 경우에는 각각의 데이터 점이 거리가 떨어져도 그 영향력이 완만하게 줄어들기 때문에 3개의 Gaussian Function이 합쳐져 왼쪽 그림과 같이 하나의 산봉우리와 같은 모양이 됩니다.

지금까지 다루었던 RBF 모델은 Regression을 위한 모델이었습니다. 3장에서도 배웠듯이 Regression을 사용해 Classification을 할 수도 있습니다. 이번에는 RBF를 사용해 Classification을 하는 방법을 알아보겠습니다.

방법 자체는 매우 간단합니다. 그저 기존의 식에 $\text{sign}$만 넣어서 Output이 $+1/-1$로만 나오게 만드는 것입니다. 다만 이번에는 Error Measure도 $(s-y)^2$로 달라지기 때문에 더 이상 In Sample Error가 0으로 고정되지 않습니다.

RBF and nearest neighbors

이번에는 RBF 모델과 비슷한 아이디어로 시작된 모델인 Nearest-neighbor method와 어떤 관계가 있는지 살펴봅시다. Nearest-neighbor method는 기존에 분류가 완료된 Training Set을 기반으로 새로운 입력이 들어왔을 때 가장 가까운 데이터와 동일하게 분류하는 간단한 분류 방법입니다. 왼쪽의 그림을 보시면 Training Set의 거리를 기반으로 정확히 중간 지점을 선으로 표현하였습니다. 새로운 데이터가 들어오면 어느 영역에 있는지를 알게 되면 즉각적으로 분류할 수 있습니다.

RBF 모델 또한 이와 비슷한 개념이기 때문에 RBF를 사용해서 Nearest-neighbor method를 구현할 수 있습니다. RBF로 Nearest-neighbor method를 표현한다면 오른쪽 그림과 같이 실린더 모양이 됩니다. 이것이 의미하는 것은 간단한데, 일정 거리까지는 최대의 영향력을 발휘하지만, 그 범위를 벗어나면 0의 영향력을 가지게 됩니다.

모양과 의미를 확인해보면 모델 자체가 굉장히 불안정한 것을 알 수 있습니다. 특히 경계선에 위치한 데이터들은 약간의 차이로 +1과 -1이 갈리게 됩니다. 이 문제를 보완하기 위해 보통은 K-Nearest-neighbor method를 사용하는데, 이것은 가장 가까운 K개의 데이터를 찾은 다음 +1이나 -1이 더 많은 쪽으로 분류하는 방법입니다. 이렇게 경계선에서 불안정성이 발생할 때 이를 보완하는 작업을 Smoothing이라고 합니다.

그렇다면 K-Nearest-neighbor method를 RBF로는 어떻게 구현하는지 알아봅시다. 기존 RBF 모델은 모든 데이터가 가설에 영향을 끼쳤기 때문에 $N$개의 데이터를 모두 사용해서 가설을 만들었고, 그렇기에 $N$개의 가중치 $w$가 있었습니다.

이제는 주어진 데이터와 가장 가까운 $K$개의 Center만 영향을 끼치게 만들어야 합니다. 그들을 각각 $\mu_1, …, \mu_K$라고 정의합니다. $\mu$는 데이터 집합의 일부일 수도 있지만, 그렇지 않고 사용자가 직접 선정한 특별한 지점일 수도 있습니다.

$\mu$를 사용해서 RBF를 수정하는 것은 간단합니다. 기존의 RBF에서 $\Sigma$에 있던 $N$을 $K$로 바꿔주고 Basis Function $\text{exp}( \cdot )$에 있던 $\mathbf{x}_n$을 $\mu_k$로 바꿔주면 됩니다.

하지만 여기에는 두 가지 문제가 있습니다. 첫째로, Center $\mu_k$를 어떻게 선택해야 할까요? 둘째로 그 때 $w_k$는 어떻게 선택해야 할까요?

먼저 Center $\mu_k$를 정하는 방법을 알아봅시다. 하나 떠오르는 방법은 전체 데이터 $\mathbf{x}_1, … \mathbf{x}_N$를 $K$개의 클러스터로 나누어 각 클러스터의 Center에서 각각의 데이터와 평균 제곱 오차를 최소화하게 만드는 것입니다.

이 방법의 장점은 이것이 Unsupervised Learning이라 $y_n$에 관계없이 구할 수 있다는 것입니다. 하지만 이 방법이 NP-Hard라는 단점이 있습니다. 쉽게 말해 시간복잡도가 다항함수로 표현될 수 없다는 것입니다.

이 NP-Hard 문제를 푸는 Iterative Algorithm으로는 Lloyd’s Algorithm이 있습니다. 아이디어는 간단합니다. 먼저 무작위로 클러스터를 정한 다음 그 클러스터를 기반으로 Center $\mu_k$를 계산합니다. 그 후에는 그 Center들을 기준으로 클러스터를 다시 만듭니다. 이 과정을 반복하면 결국에 Center들은 특정한 점들로 수렴하게 됩니다. 한 가지 문제는 이것이 Global Minimum이 아니라 Local Minimum으로 수렴하게 된다는 것입니다.

Lloyd’s Algorithm을 간단하게 표현하면 다음과 같습니다.

1. 데이터 점들을 얻습니다.
2. 지금은 $y$를 배제하고 $\mathbf{w}$만 갖고 수행합니다.
3. 무작위로 Center를 정합니다. 몇 개의 Center를 정하는 것도 문제이지만, 여기서는 Support Vector와 비교하기 위해 Support Vector와 똑같은 수인 9개로 정했습니다.
4. 주어진 Center를 기반으로 클러스터링을 하고, 그 클러스터링에서 새로운 Center를 찾습니다. 이 과정을 반복합니다.
5. 더 이상 Center가 이동하지 않는다면 바로 그 점이 최종 $\mu$ 입니다.

이 방법을 통해 데이터들을 분류한다면 위 슬라이드의 오른쪽 그림과 같습니다. 예제에서 좋지 않은 분류가 하나 나왔는데, 바로 가장 왼쪽 아래에 있는 Center입니다. 이 Center를 포함한 클러스터는 $+1$과 $-1$을 모두 갖고 있기 때문에 RBF가 제 역할을 하지 못하지만, 강의에서는 이 정도는 Unsupervised Learning을 사용할 때 감수해야 한다고 합니다.

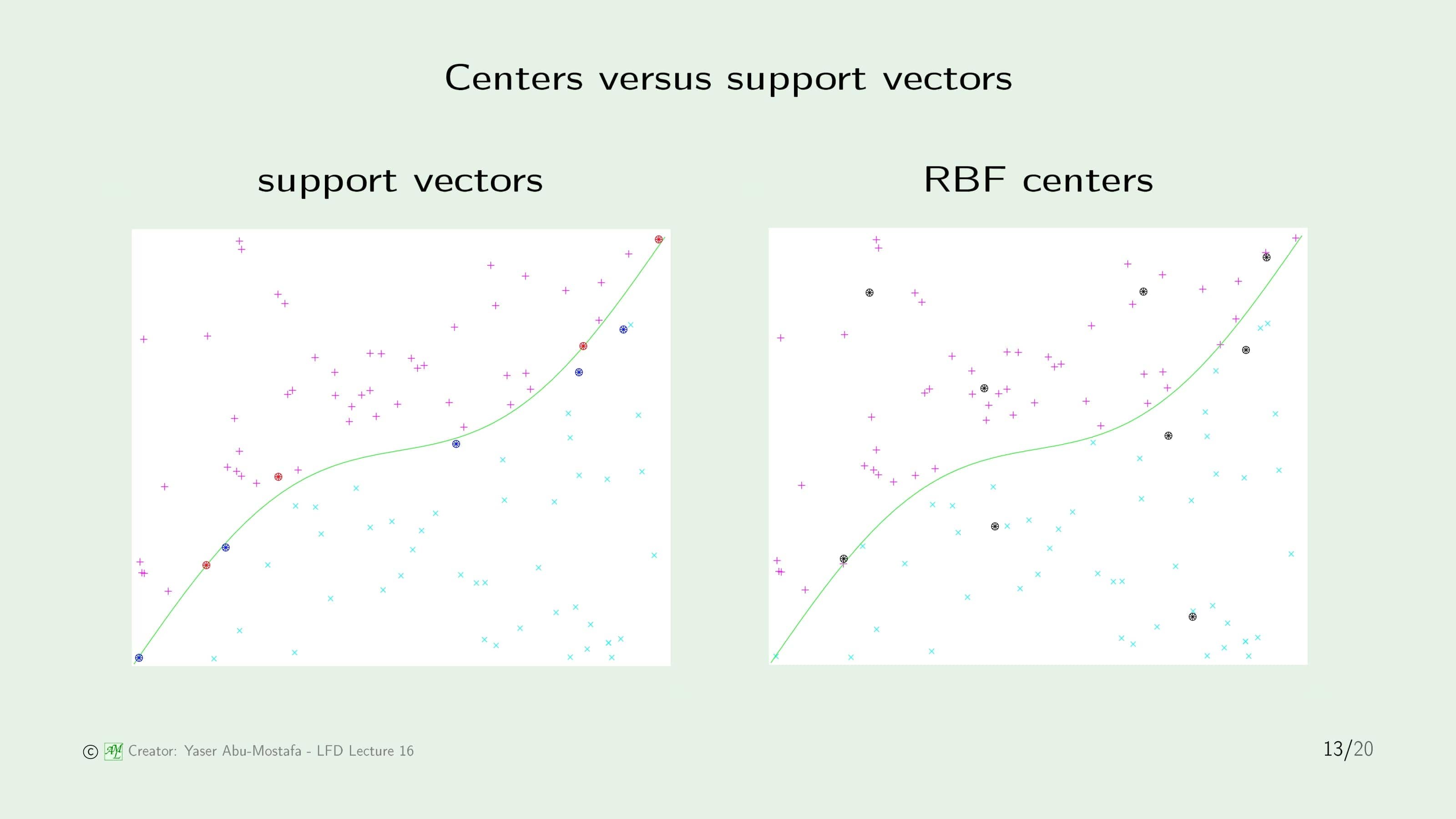
14장에서 배운 Support Vector도 데이터 집합을 대표하는 점이었고, RBF의 Center도 데이터를 대표하는 점입니다. 이 둘을 한번 비교해봅시다. 이 둘은 똑같이 데이터를 대표하는 점이지만 구하는 방법부터 하는 역할까지 모두 다릅니다. 차이점을 간단하게 정리하면 아래와 같습니다.

1. Support Vector는 Supervised Learning으로 구하지만, RBF Center는 Unsupervised Learning으로 구한다.
2. Support Vector는 무조건 데이터 집합의 점 중 하나이지만, RBF는 그럴 수도 있고, 아닐 수도 있다.
3. Support Vector는 Separating Surface (분리 평면)을 표현하지만, RBF Center는 데이터 입력을 표현한다.
4. 각각의 Support Vector는 $+1/-1$로 구분되지만 RBF Center는 Label이 없다. ($=y_n$을 사용하지 않는다)

이제 RBF의 Center $\mu$를 모두 구했으니, 남은 것은 가중치 $w$를 구하는 것만 남았습니다.

그런데, 아까와는 다른 문제가 생겼습니다. 처음 모든 데이터 집합을 사용했을 때는 방정식이 $N$개, 미지수가 $N$개로 동일했기 때문에 In Sample Error를 정확하게 0으로 만드는 가중치 $w$를 찾았지만, 이제는 방정식이 똑같이 $N$개인 상황에서 미지수가 $K$개로 줄어든 상황이 되었습니다.

고등학교 때 배운 기억을 되살려보면, 방정식의 개수가 미지수의 개수보다 많을 때는 풀지 못한다고 배웠습니다. 그렇기 때문에 여기서는 식을 약간 변형시킵니다. 아까는 데이터 $(\mathbf{x}_n, y_n)$를 대입시켰을 때 정확하게 일치했기 때문에 $=$로 표현했지만, 이제는 약간의 In Sample Error를 감수해야 하므로 $\approx$로 표현합니다.

이렇게 하고 나면 나머지는 이전과 똑같이 행렬로 표현할 수 있습니다. 다만 이제는 $\Phi$가 정사각행렬이 아니기 때문에 역행렬이 존재하지 않습니다. 그렇기 때문에 $w$를 구하려면 3장에서 배운 의사역행렬(Pseudo-Inverse)를 사용해야 합니다.

이제는 RBF를 Graphic Network로 표현해 보겠습니다. 이 그림은 Basis Function $\text{exp}(-\gamma \lVert \mathbf{x} - \mu_k \rVert^2)$을 $\phi$로 표현한 그림입니다.

아래쪽부터 본다면 데이터 점 $\mathbf{x}$가 각각의 Center $\mu_1, …, \mu_K$와의 거리를 계산하는 것부터 시작합니다. 그리고 나서 각각의 거리를 제곱한 후, $-\gamma$를 곱해 Exponential $e$의 지수에 넣습니다. 최종적으로 이것들을 전부 더해주고 나면 $h(\mathbf{x})$가 도출됩니다. (이 더하는 과정에서 Bias Term $b$ 혹은 $w_0$가 더해질 수도 있습니다.)

그런데 이 구조는 어디서 많이 본 것 같은 구조입니다. 이 RBF Network를 가로로 눕혀서 본다면 Neural Network와 비슷한 모양이 됨을 유추할 수 있습니다.

RBF and neural networks

그렇다면 RBF Network와 Neural Network를 서로 비교해봅시다. 비교를 쉽게 하기 위해, 오른쪽의 Neural Network는 고의적으로 RBF Network와 유사한 구조로 디자인하였습니다.

역시 비교를 위해서는 아래쪽 부분부터 살펴봅시다. RBF Network의 $\lVert \mathbf{x} - \mu \rVert$ 부분은 데이터와 Center의 거리가 멀다면 $\phi$를 지날 때 0에 수렴할 것입니다. 즉, Network Output의 기여도가 0에 수렴할 것입니다. 반면 Neural Network에서는 $\mathbf{w} \mathbf{x}$의 값이 크든 작든 Sigmoid 함수를 통과할 것이고, Sigmoid 그래프의 특성상, 이 값은 언제나 Network Output에 일정 부분 기여를 한다는 것을 알 수 있습니다.

이제 선택할 마지막 변수는 Gauss Function에서의 $\gamma$ 입니다. 슬라이드 6에서 보았듯이 $\gamma$의 크기에 따른 변화가 적지 않기 때문에 적절한 $\gamma$를 찾는 것은 매우 중요합니다. $\gamma$를 구할 때는 일반적으로 Gradient Descent를 사용해서 In Sample Error가 가장 낮게끔 선택합니다.

여기에 또 문제가 있습니다. 왜냐하면 Pseudo Inverse로 $w$를 구할 때는 $\gamma$ 값을 알고 있다는 가정 하에 계산하기 때문입니다. 따라서 반복적인 방법으로 $\gamma$를 계산합니다. 여기에 사용하는 알고리즘은 Expectation Maximazation (EM) Algorithm 이라고 부릅니다.

이 알고리즘의 아이디어는 Lloyd’s Algorithm과 유사합니다. 먼저 $\gamma$를 임의의 값으로 고정한 후, 가중치 $w_1, … ,w_K$를 계산합니다. 그 다음에는 반대로 가중치 $w_1, … ,w_K$를 고정한 후 In Sample Error를 최소화하는 $\gamma$를 계산합니다. 여기서는 $\gamma$를 단 1개의 매개변수로 가정했지만, 각 Center 별로 $\gamma$의 값을 다르게 하는 경우도 동일하게 처리할 수 있습니다.

RBF and kernel methods

이제 RBF와 Kernel Method, 그리고 Regularization과의 연관성을 빠르게 짚고 마치겠습니다.

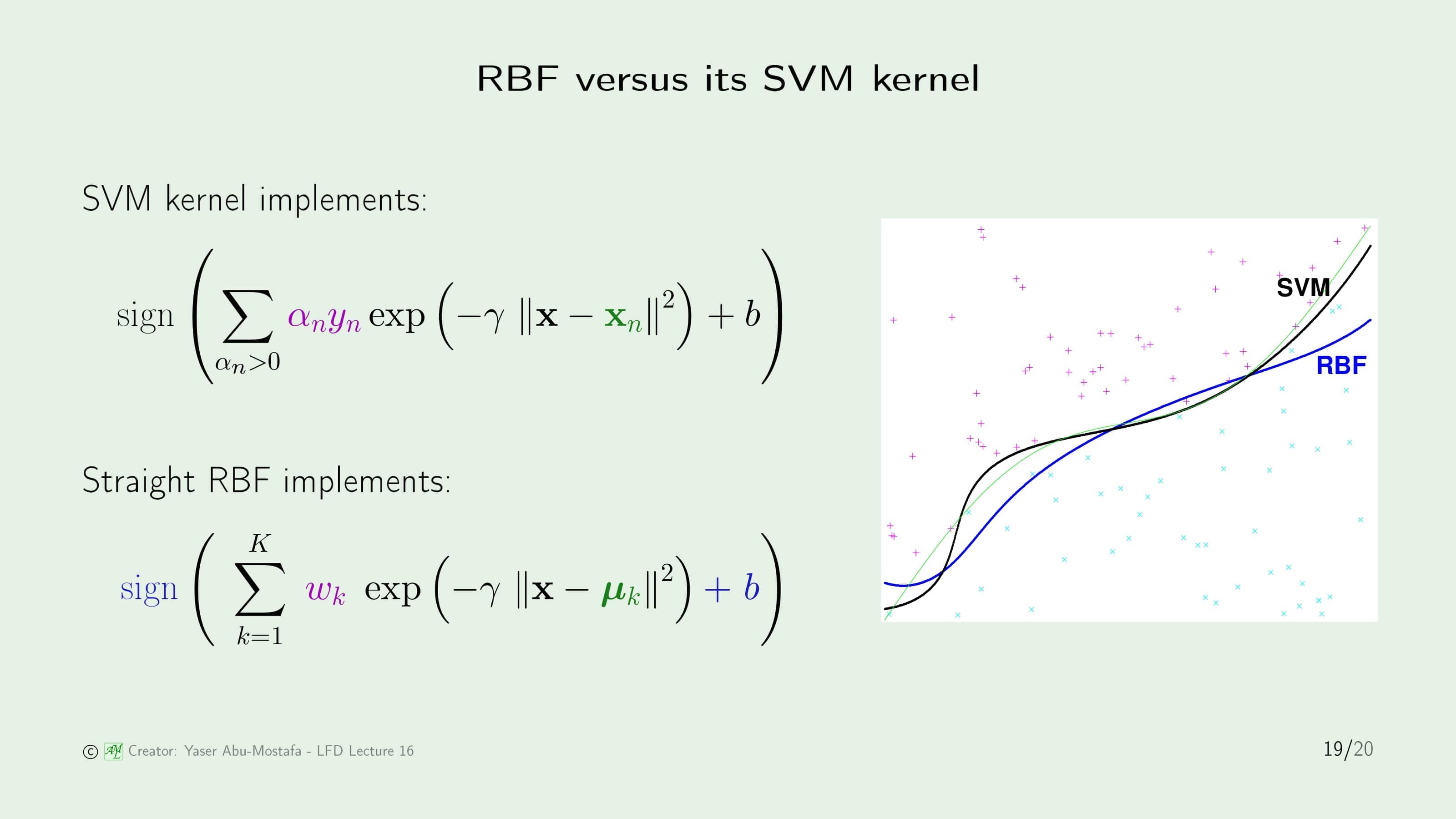
15장에서 Kernel Method를 배울 때 잠깐 RBF Kernel을 언급했었습니다. 이번에는 SVM Kernel과 RBF를 사용한 Classification이 어떻게 다른지를 살펴보겠습니다. (RBF 식에서 $\text{sign}$과 $b$가 파란색 글씨로 나온 이유는 없어도 되는 부분이기 때문입니다.)

결과만 놓고 보았을 때 오른쪽 그림을 보시면 SVM이 RBF보다 더 잘 Classification 한 것을 볼 수 있습니다. 하지만 이것만 놓고 보았을 때 SVM이 RBF보다 우수하다고 판단할 수는 없습니다. 왜냐하면 이 문제에서의 Support Vector는 9개가 나오는데, RBF가 동등한 조건에서 경쟁하기 위해 $K$를 9로 놓았기 때문입니다. 이전 문제에서도 보았듯이, Center를 9개로 정하는 것이 이 문제에서 최선의 방법이 아니기 때문에 RBF 입장에서는 조금 불공평한 경쟁이라고 볼 수 있습니다.

RBF and regularization

마지막으로 RBF와 Regularization의 연관성을 정리하겠습니다. Regularization을 통해 RBF를 유도할 수 있습니다. 간단한 예시를 만들기 위해, 데이터는 1차원 입력이라고 가정하겠습니다. 이 데이터로 가설 $h$를 만들고, Squared Error를 계산하면 $(h(x_n) - y_n)^2$ 이 됩니다. 이것을 모든 데이터에 대해 수행해 준 다음 더하게 되면 In Sample Error가 나오는데, 이 자체만 Minimize 하게 되면 Overfitting이 발생하여 $\lambda$를 포함한 추가 항을 더한 다음 Minimize 하는 방법이 Regularization이었습니다.

여기서는 $\lambda$ 항에 가설 $h$를 입력 $x$에 대해 $k$번 미분한 것의 크기(제곱)를 $-\infty$부터 $\infty$까지 적분해준 값에 상수 $a_k$를 곱해 $k=0$부터 $k=\infty$까지 더한 항을 곱해주었습니다. 왜 이런 식을 해야 하는지는 강의에서도 너무 복잡한 과정이라서 생략하였는데, 이런 Regularization을 수행하면 그 결과가 바로 RBF와 정확하게 일치한다고 설명하였습니다.

이것은 Smoothest Interpolation (가장 매끄러운 보간)이라고 하며 RBF에 대한 또 다른 해석이라고 합니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.