Validation

13장에서는 Overfitting을 해결하는 방법 중 Validation (검증)이라는 방법을 배우게 됩니다.

Outline

이번 장은 Validation Set (검증 집합), Model Selection (모델 선택), Cross Validation (교차 검증) 순서대로 배우게 됩니다. Validation이 무엇인지 알지 못하는 지금은 소제목을 봐도 이해가 쉽지 않으니 일단 넘어가도록 합시다.

The validation set

기본적으로 Out of Sample Error는 In Sample Error에 Overfit penalty $\Omega$를 더한 식으로 표현되었습니다. 이 Overfit penalty를 없애기 위해 Regularization (정규화)에서는 이 penalty의 수치를 추정하는 것을 목표로 하였고, 이를 Augmented Error로 호칭하였습니다.

이것과 다르게 Validation (검증)은, Out of Sample Error를 추정하고 오류를 최소화합니다. 이것을 측정하는 방법은 Test Set과 유사합니다.

Out of Sample Data $(\mathbf{x}, y)$에 대해, Error는 $\mathbf{e}(h(\mathbf{x}, y))$로 정의하는 것을 이미 이전에 배웠습니다. 그 Error을 측정하는 대표적인 두 가지 방법인 Squared Error와 Binary Error도 이미 배웠습니다.

검증에서 하려고 하는 것은 이 Error의 추정치이기 때문에, 기대값인 $\mathbb{E}[\mathbf{e}(h(\mathbf{x}, y))]$라 표현할 수 있습니다. 이것은 Bias가 없는 Out of Sample Error 입니다. Variance는 따로 표현해주어야 하기 때문에 Error의 Variance를 $\sigma^2$로 정의하겠습니다.

Out of Sample Error를 추정하는데에는 Out of Sample과 별개의 데이터인 Validation Set을 사용합니다. Validation Set은 $K$개의 데이터를 보유하고 있다고 가정합니다. 이 때의 Error 측정은 In Sample Error를 계산하는 방법과 동일하지만, 호칭을 구분하기 위하여 $E_{val}$ (Validation Error)로 표현합니다. 기존의 방법과의 차이점은 Sample Data와는 별개의 데이터로 수행된다는 점입니다.

Validation Error의 평균을 계산하기 위해서는 간단하게 $E_{val}$에 기대값만 취해주면 되고, $\mathbb{E}$는 시그마 합 안쪽으로 넣을 수 있습니다. 그러고 나면 이것은 바로 이전 슬라이드에서 했던 Out of Sample Error와 동일함을 알 수 있습니다. 즉, Validation Set만으로 Out of Sample Error를 측정할 수 있다는 것을 보인 것입니다.

이번엔 Validation Error의 Variation을 계산해보겠습니다. Variance 역시 Validation Error를 통해 계산하는데, 이때 Variance와 Co-Variance이 계산과정에서 같이 나옵니다. 하지만 운이 좋게도 데이터를 독립적으로 뽑았기 때문에, Co-Variance는 모두 0이 되고, Variance만 남게 됩니다. 분모는 이 과정에서 $K^2$으로 바뀌게 됩니다. 결과적으로, Validation Error의 Variation은 Out of Sample Error를 Validation Set의 원소의 수로 나눈 것이 됩니다.

마지막으로 Validation Error와 Out of Sample Error 사이의 관계를 정리하면, Validation Error는 Out of Sample Error에 $\frac{1}{\sqrt{K}}$차수의 식을 더하거나 뺀 수치가 됩니다. $K$가 크면 클 수록 이 부분은 0에 가까워지므로, Validation Set이 클수록 Out of Sample Error를 더 정확하게 추정할 수 있습니다.

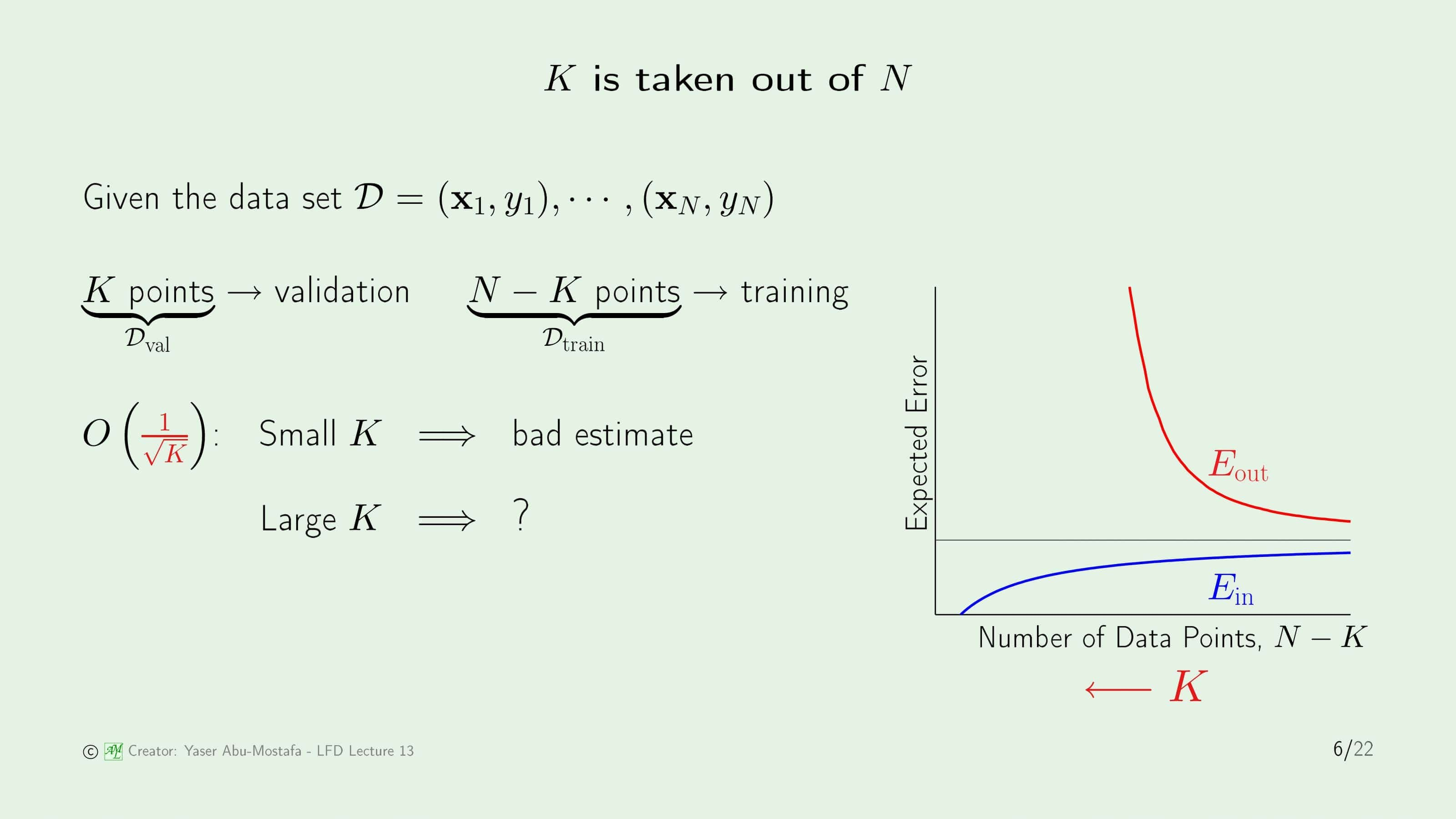
하지만 Validation Set을 늘리는 데에는 한계가 있습니다. 기본적으로 Validation Set은 Traning에 사용되는 Data Set인 $\mathcal{D}$에서 일부를 가져와야하기 때문입니다. 전체의 $N$개의 데이터에서 $K$개 만큼의 데이터를 Validation을 위해 사용하게 되면 Training에 사용되는 데이터의 수는 $N-K$개가 됩니다.

만약에 $K$가 작다면, $O( \cdot )$이 커지기 때문에 Validation Error와 Out Of Sample Error의 차이가 커지므로 제대로 된 측정을 할 수 없는 문제가 생깁니다. 반대로 $K$가 너무 크다면 Traning의 데이터 수가 적으므로 오른쪽 그림처럼 In Sample Error와 Out of Sample의 차이가 커지는 문제가 생기는 것을 알 수 있습니다.

그럼 이렇게 생각해볼 수 있습니다.

“Validation에 사용한 $K$개의 데이터를 Training에 사용하면 되지 않을까?”

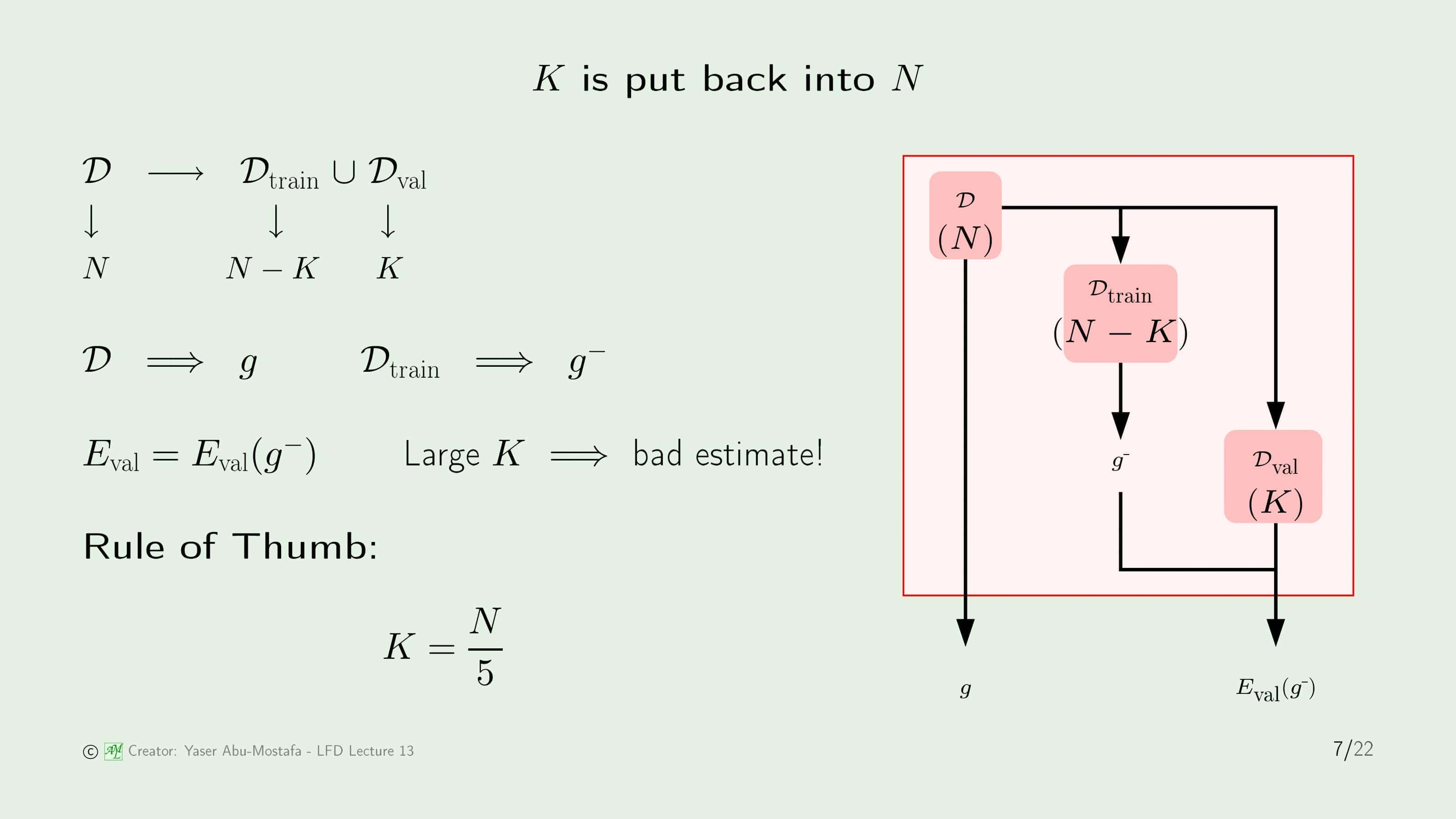
이 질문에 답하기 위하여, 처음부터 차근차근 정리해봅시다. 먼저 주어진 전체 데이터 집합은 $\mathcal{D}$입니다. $\mathcal{D}$는 Training set $\mathcal{D}_{train}$과 Validation set $\mathcal{D}_{val}$의 합집합니다. $N$개의 데이터 중 $N-K$개의 데이터로 학습하고, $K$개의 데이터로 Validation을 하였습니다.

전체 데이터 집합 $\mathcal{D}$를 사용하여 Training 하게 되면, 최종 가설인 $g$를 얻습니다. 그런데 $\mathcal{D}_{train}$을 사용해서 Training 하게 되면, 최종 가설로 $g$가 아니라 $g^{-}$를 얻게 됩니다.

정리하자면, Validation Set을 포함하여 Training을 하게 된다면, 최종 가설은 $g$인데 Validation Error의 결과는 $g^{-}$에 대해 나오게 됩니다. 만약 $K$가 작다면 $g$에 대한 Validation Error나 $g^{-}$에 대한 Validation Error나 비슷하기 때문에 큰 문제가 되지 않습니다. $K$가 크다면 $g$와 $g^{-}$ 사이의 차이가 더욱 커지기 때문에 Validation Error 자체의 의미가 사라지게 됩니다.

결론적으로 Validation Set 크기만 잘 조정한다면 Validation에 사용한 데이터를 Training에 사용해도 문제가 없습니다. 강의에서는 대략적으로 전체 데이터의 20%를 Validation Set으로 사용하는 것이 Rule of Thumb (경험적 법칙)이라고 제시하고 있습니다.

가만히 생각해보면 Validation에서 사용한 방법은 Test를 할 때 쓰는 방법과 차이가 없습니다. 그렇다면 왜 이것을 Validation 이라고 부르는 것일까요? 강의에서는 이렇게 말하고 있습니다.

“We call it validation, because we use it to make choices.”

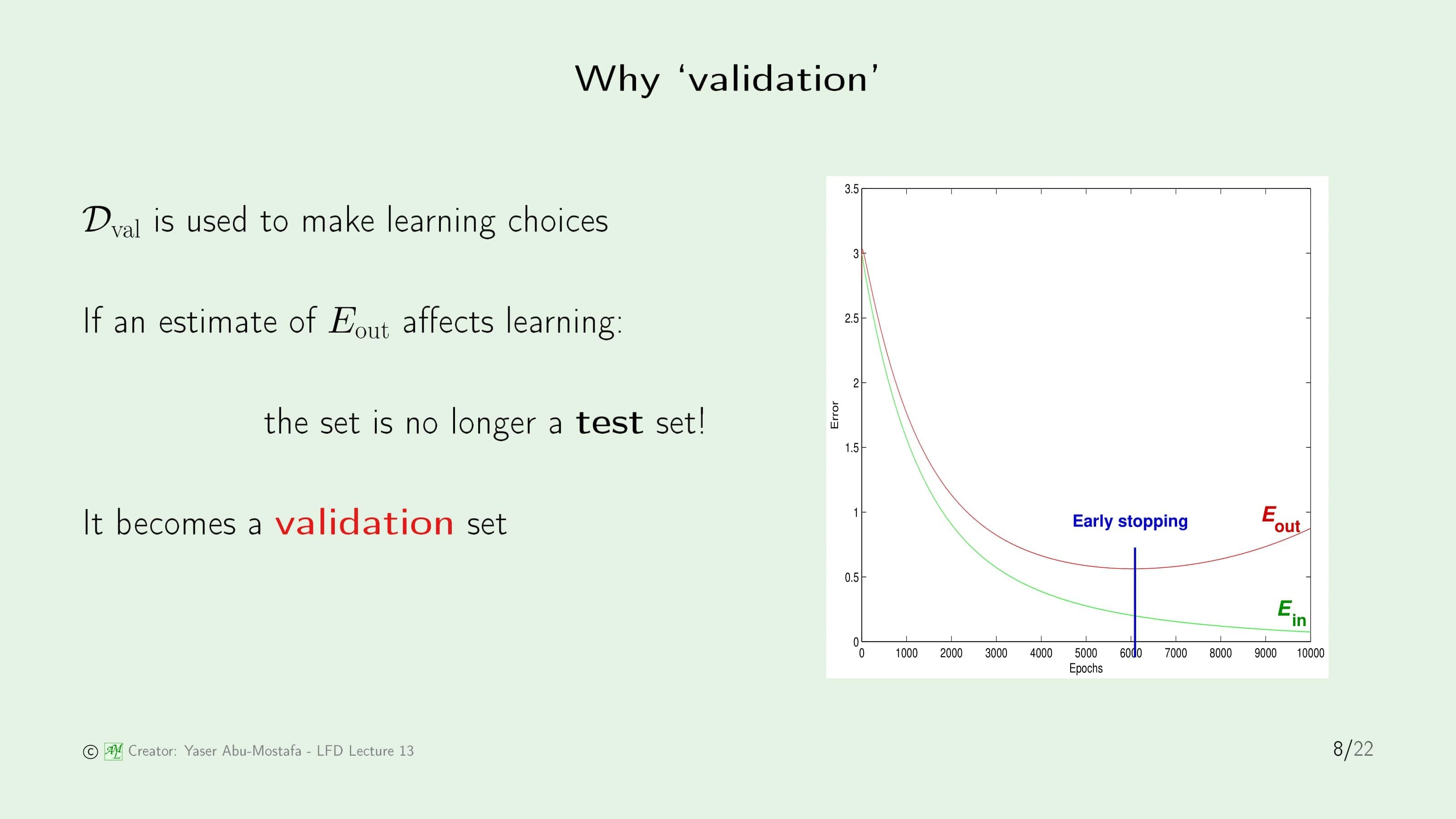
선택하기 위해 사용하므로 Validation이라고 부른다고 합니다. 무엇을 선택하는 걸까요? 오른쪽 그림을 보시면 답이 나옵니다. 이 그림은 11장에서 Overfitting을 배울 때 나왔습니다. 이 그림에서 가장 좋은 성능을 보이는 지점은 Early Stopping 부분입니다. 하지만 이 당시에는 Out of Sample Error를 예측할 수 없었기 때문에 Early Stopping 지점에 도달하더라도, 이 다음에 Out of Sample Error가 증가할지, 감소할지를 알 수 없었기 때문에 계속 Training을 진행하였습니다. 결과적으로 이것이 Overfitting을 일으키는 요소였던 것입니다. Validation을 함으로써 Out of Sample Error를 예측할 수 있으니, Early Stopping 부분에 도달한다면 이 지점을 기준으로 Out of Sample Error가 증가할 것이라는 것을 알고 멈출 수 있습니다. 따라서 이것이 Validation이라고 부르는 이유입니다.

그렇다면 Test Set과 Validation Set의 차이점을 알아보겠습니다. Test Set은 Bias가 없지만 Validation Set은 Optimistic Bias를 가지고 있습니다.

Optimistic의 의미를 이해하기 위해 간단한 예를 들어보겠습니다. Out of Sample Error가 0.5로 같은 2개의 Hypothesis $h_1$과 $h_2$를 가정해봅시다. 두 개의 Hypothesis에서 각각 Error를 예측하는데, $h_1$의 Error 추정값을 $\mathbf{e}_1$, $h_2$의 Error 추정값을 $\mathbf{e}_2$라 정의합니다. 단순하게 하기 위해, 두 Error 추정이 모두 0과 1 사이에서 균일(Uniform)하다고 가정하겠습니다.

여기서 $\mathbf{e}_1$과 $\mathbf{e}_2$ 모두 Bias가 없는 Out of Sample Error의 추정입니다. 여기서, 두 개의 가설 $h_1$과 $h_2$ 중 하나를 고르는 것을 $h$라 부르겠습니다. 고르는 방법은 $\mathbf{e}_1$과 $\mathbf{e}_2$ 중 작은 것입니다. 그렇다면 $\mathbf{e}$의 기대값은 얼마일까요?

$\mathbf{e}_1$과 $\mathbf{e}_2$ 모두 기대값이 0.5이므로 $\mathbf{e}$ 또한 0.5라고 단순하게 생각할 수도 있으나, 실제로는 0.5보다 작을 수밖에 없습니다. 왜냐하면 2개의 확률 변수 중 작은 것을 고르는데, 두 확률 변수의 평균이 0.5 이므로, 항상 작은 것만 고르게 된다면 확률 분포가 0과 1 사이에서 균일하게 있다는 가정 하에서 0.5보다 작은 것을 뽑을 확률이 75%나 되기 때문입니다. 따라서 대부분의 경우 $h$의 Error가 0.5보다 낮기 때문에 Optimistic Bias라고 부르는 것입니다.

Model selection

다음으로, Validation의 모델을 선택하는 방법에 대해 알아보겠습니다.

먼저 M개의 모델 $\mathcal{H}_1, …, \mathcal{H}_M$이 존재한다고 가정해봅시다. Validation Set을 제외한 데이터 집합인 $\mathcal{D}_{train}$을 사용하여 학습하면 최종 가설로 $g_m^{-}$이 각 모델마다 생성됩니다. 마찬가지로 $\mathcal{D}_{val}$ 집합으로 Validation Error를 각 모델별로 측정한 결과도 $E_1, \ldots, E_M$로 나오게 됩니다. 이 중에 가장 좋은 결과를 가진 Validation Error을 골라 $E_{m^*}$라고 하는데, 이전에 설명한대로 그 과정에서 Optimistic Bias가 포함되어 있음을 알 수 있습니다.

최선의 가설 $\mathcal{H}_{m^*}$을 찾는 것도 이와 크게 다르지 않습니다. 이 때의 학습은 $\mathcal{D}_{train}$이 아니라 $\mathcal{D}$를 사용합니다. 이렇게 고른 $E_{m^*}$과 $\mathcal{H}_{m^*}$이 최종 가설 $g_{m^*}$이 되는 것입니다. 오른쪽의 그림에서 이를 잘 표현하고 있으니 참고하시면 이해가 쉬울 것입니다.

이 Bias에 대해 조금 더 자세하게 다뤄보겠습니다. 모델 선택은 이전 슬라이드에서 언급했듯이 $\mathcal{D}$가 아닌 $\mathcal{D}_{val}$을 기준으로 합니다. 그렇기에 $g_{m^*}$에 대한 Validation Error는 Out of Sample Error로부터 Bias됩니다.

오른쪽 그림은 Validation Set Size에 따른 Validation Error와 Out of Sample Error의 변화를 나타내고 있습니다. Validation Set Size가 커질수록 학습에 사용할 데이터의 수가 적어지므로 두 Error가 커지는 것은 이전에 배웠습니다. 하지만 여기서 주목할 것은 Validation Set Size이 커질수록 두 Error의 그래프가 가까워진다는 것입니다. 왜 그런지는 다음 슬라이드에서 그 이유를 보여드리겠습니다.

주어진 데이터 중 Validation Set을 제외한 데이터 집합 $\mathcal{D}_{train}$을 사용하여 $M$개의 모델 $\mathcal{H}_1, …, \mathcal{H}_M$로 최종 가설을 도출하면, 그 결과는 각각 $g_1^{-}, …, g_M^{-}$이 됩니다. 이것들을 원소로 하는 새로운 모델을 $\mathcal{H}_{val}$이라 부르겠습니다. 최종 가설은 이 모델의 원소 중 Validation Error가 가장 작은 것이 됩니다.

이전에 Hoeffding Inequality와 VC Bound에서 배웠던 내용을 이용하여, Validation Error와 Out of Sample Error의 관계를 유도합니다. 여기서 Validation Error는 VC Bound에서 사용했던 In Sample Error의 역할을 하게 되고, 여러 모델의 합은 그냥 간단하게 Union Bound로 가정합니다.

이 관계식을 유도하고 나면 $O( \cdot )$ 부분이 중요합니다. Validation Set Size $K$가 커질수록 $O( \cdot )$ 가 작아짐을 쉽게 알 수 있습니다. $O( \cdot )$가 매우 작다면 Out of Sample Error와 Validation Error가 거의 같아짐 또한 알 수 있습니다. 이로써 이전 슬라이드에서 Validation Set Size가 커질수록 두 그래프가 가까워지는 이유를 알 수 있게 되었습니다.

이제 지금까지 발생했던 데이터 오염을 정리해보겠습니다. Out of Sample Error은 방금 전까지 다루었듯이 Optimistic Bias로 오염되었습니다. 이 외에 Error를 추정하는데 사용했던 3가지 집합은 어떤지 보겠습니다. 첫째로, In Sample Error를 측정하는데 사용했던 Training Set은 애초에 이것으로 학습을 했기 때문에 완전히 오염되었다고 판단합니다. 둘째로, Test Error를 측정하는데 사용했던 Test Set은 학습에 관여하지도 않고 어떠한 의사결정도 하지 않았기 때문에 완전히 깨끗한 집합니다. 마지막으로 Validation Error를 측정하는데 사용했던 Validation Set은 Out of Sample Error를 추정하고 어디서 학습을 멈춰야 하는지 사용되었기 때문에 약간 오염되었다고 판단할 수 있습니다.

Cross validation

마지막으로 Cross Validation (교차 검증)에 대해 배우겠습니다.

먼저 Validation Set Size $K$의 딜레마를 다시 짚고 넘어가겠습니다. 일단 우리가 원하는 것은 Validation Error가 $\mathcal{D}_{train}$으로 학습한 최종 가설의 Out of Sample Error와 최대한 비슷한 것과 이것이 $\mathcal{D}$의 Out of Sample Error와 최대한 비슷한 것을 원합니다. 그런데 첫 번째로 원하는 것을 만족시키려면 $K$가 최대한 커야하고, 두 번째로 원하는 것을 만족시키려면 $K$가 최대한 작아야합니다.

혹시 두 가지 요구사항을 모두 만족시키는 방법은 없을까요?

여기서 이를 해결하기 위해 Cross Validation의 한 방법인 Leave one out 이라는 방법을 소개합니다. 약간의 수학적인 트릭을 이용한 것인데 방법을 보시면 굉장히 머리를 잘 썼다는 것을 느낄 수 있습니다.

이 방법은 Validation으로 단 1개의 데이터만 사용합니다. 나머지 $N-1$개의 데이터는 모두 Training에 사용합니다. 전체 데이터에서 1개만을 제외한 데이터이기 때문에 $g^{-}$는 $g$에 매우 가깝다는 것을 알 수 있습니다. 우선 여기서 딜레마의 두 번째 조건을 만족함을 알 수 있습니다.

편의상 제외한 데이터를 $(\mathbf{x}_n, y_n)$이라 부르고, 나머지 $N-1$개의 데이터를 사용하여 만든 최종 가설을 $g^{-}_n$이라 부르겠습니다. 그렇다면 Validation Error는 오직 이 1개의 점에서의 Error이므로, $\mathbf{e}(g^{-}_n(\mathbf{x}_n, y_n))$이 됨을 알 수 있습니다.

Cross Validation은 이 과정을 모든 데이터에 대해 실시하는 것입니다. 그 후 이들의 평균을 구하면 Cross Validation이 완성된 것입니다. 결과적으로 모든 데이터를 Validation에 사용했기 때문에 Validation Set이 데이터 $N$개 전체가 되었습니다. 이로써 딜레마의 첫 번째 조건을 만족했습니다.

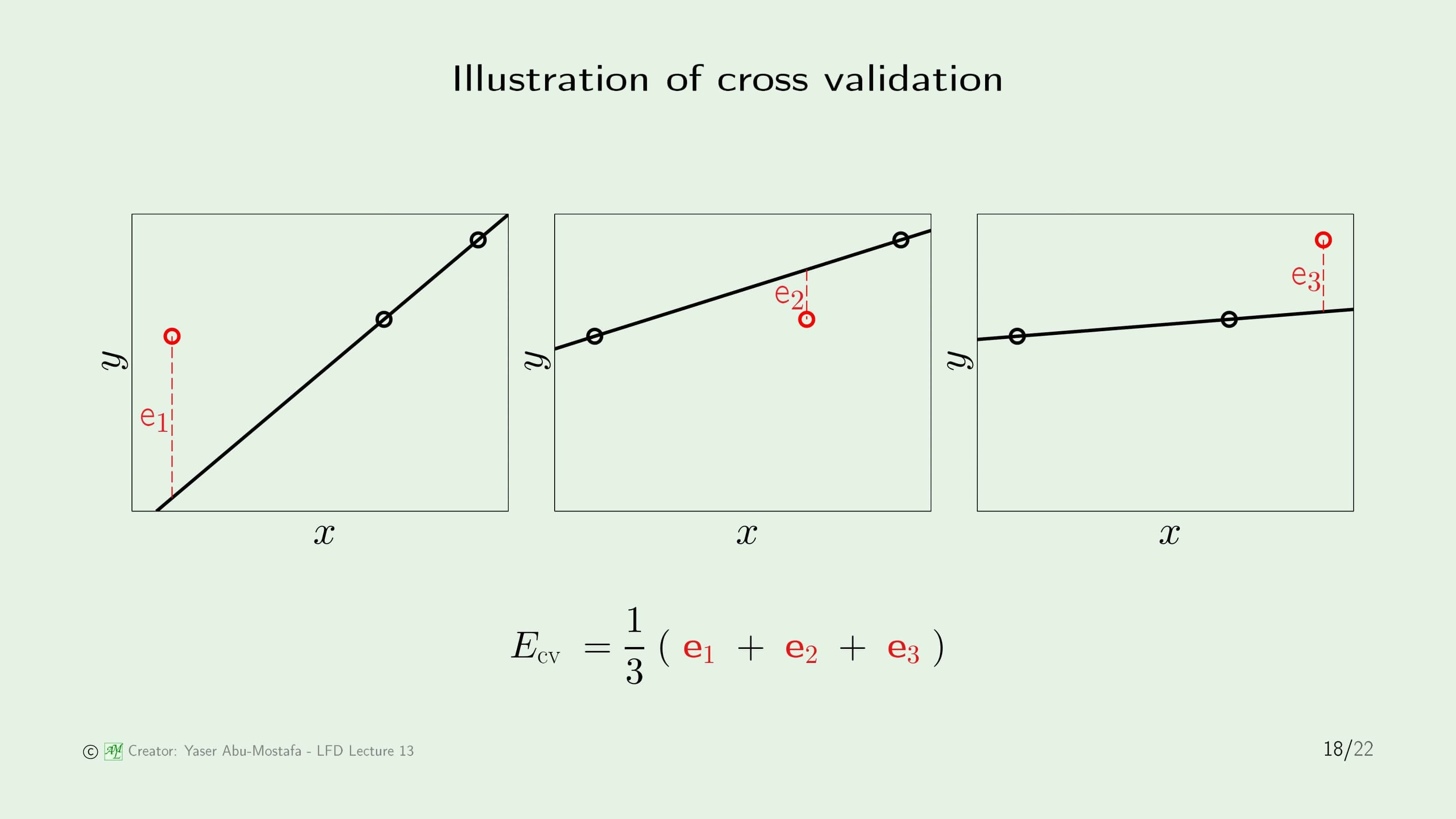
Cross Validation을 이해하기 쉽게 하나의 예를 들어보겠습니다. 3개의 데이터가 존재하고, 선형 모델을 사용할 것입니다. 편의상 왼쪽부터 데이터를 한번씩 빼고, 나머지 2개로 만든 가설을 만듭니다. 그 후, 만든 가설과 제외한 데이터 사이의 Error를 측정합니다. 이렇게 나온 Error는 각각 $\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3$이 됩니다. Cross Validation Error는 이 3개에 대한 평균을 구하면 간단하게 구할 수 있습니다.

그럼 이제 Cross Validation을 사용하여 모델을 선택하는 것을 보겠습니다. 상수 모델을 하나 추가하여 이전 슬라이드에서 계산한 선형 모델과 비교해봅시다. Cross Validation Error의 정확한 값은 나와있지 않지만, 눈으로 대충 비교해봐도 상수 모델의 Cross Validation Error가 더 낮음을 쉽게 알 수 있습니다.

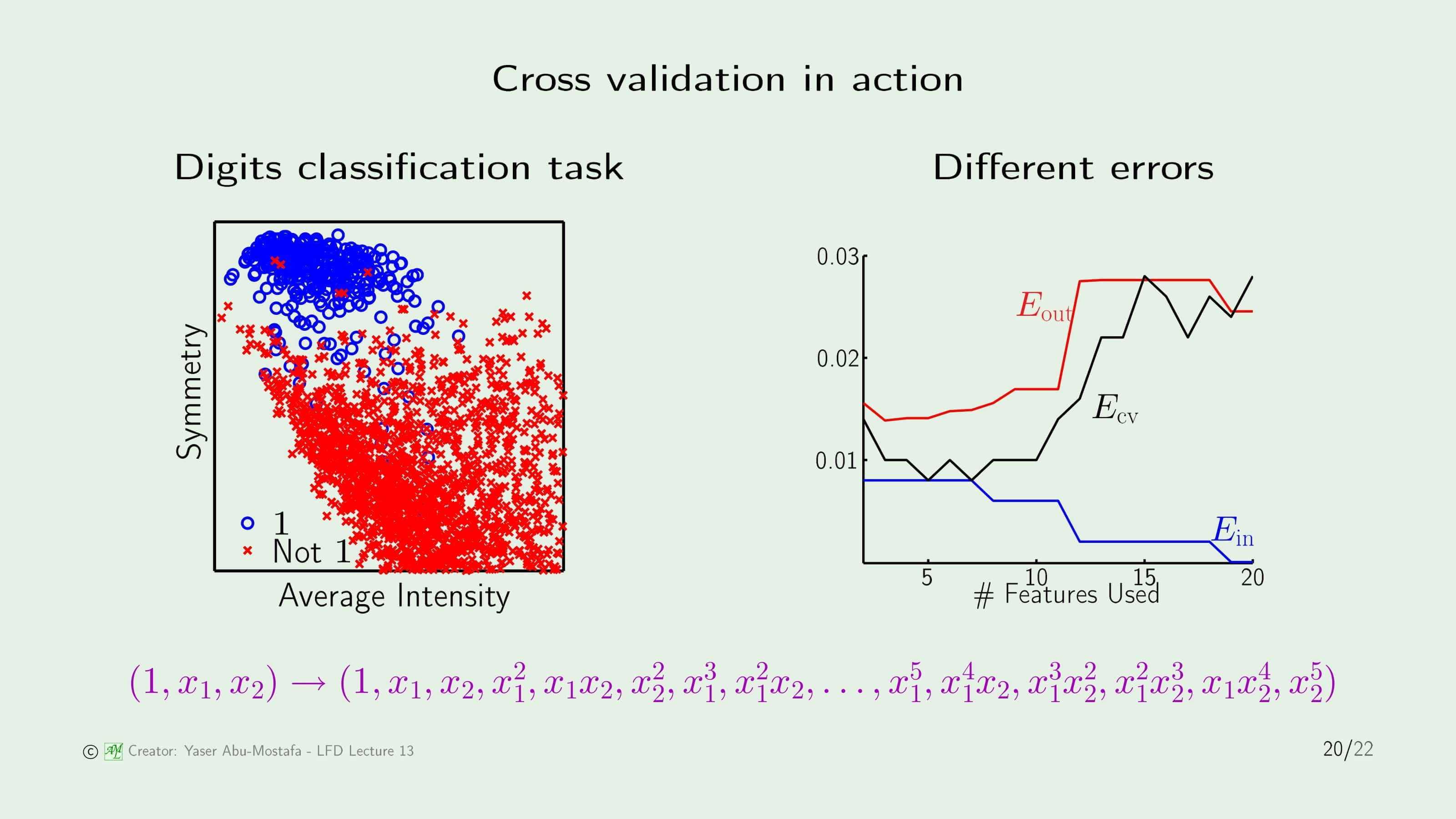
좀 더 복잡한 예제를 보도록 합시다. 이 예제는 예전에 했던 손글씨를 분류하는 학습입니다. 원래의 문제를 조금 단순화 시켜 이 글씨가 1인지 1이 아닌지만을 판단하는 Classification입니다. 이 문제는 Nonlinear Transform을 사용하였습니다.

이 경우에는 5차식을 사용하여 Transform을 하였는데, Transform Vector의 차원의 수는 총 20입니다. 오른쪽 그림은 Transform 차원을 1부터 20까지 사용하며 In Sample Error, Out of Sample Error, Cross Validation Error의 변화를 보여주고 있습니다. 어떤 Transform을 사용했는지에 따라 모델이 달라지므로, 총 20개의 모델이 있는 것과 같습니다. 우리는 가장 낮은 Cross Validation Error를 가진 모델을 선택해야 하는데, 그래프를 보면 5 또는 7 차원을 모델을 선택해야 함을 알 수 있습니다.

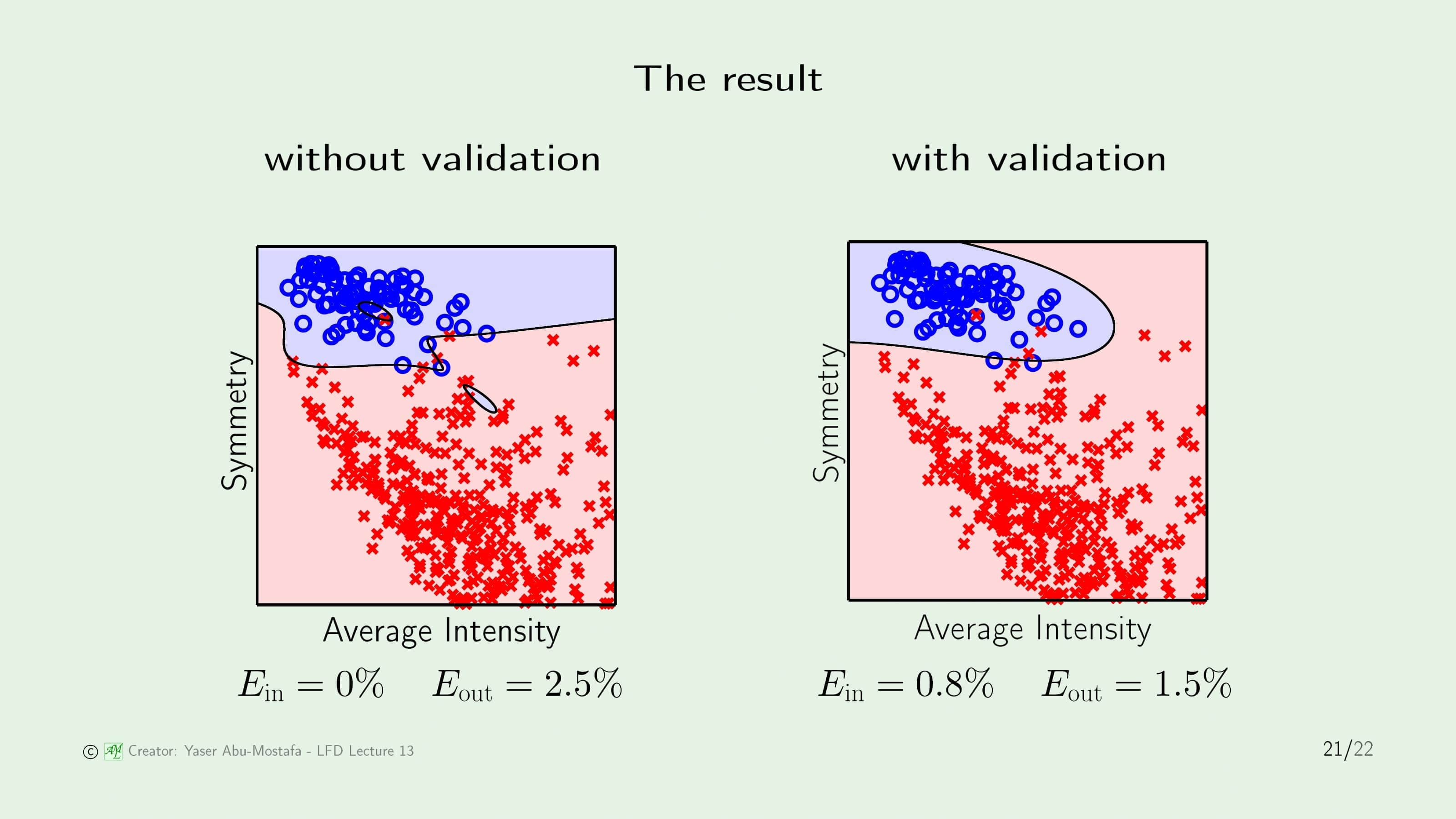
이 문제에서 Validation을 사용하지 않은 것과 사용한 것이 어떤 차이가 있는지 비교해 봅시다. 왼쪽은 Validation을 사용하지 않은 경우인데, Overfitting이 일어난 것을 쉽게 알 수 있습니다. In Sample Error는 0이지만, 주어진 데이터에 과도하게 맞추다보니 빨간색 영역 중간에 파란색 영역이 일부 존재함을 알 수 있습니다.

오른쪽은 Validation을 사용한 것인데, In Sample Error는 조금 증가했지만, Out of Sample Error가 사용하지 않은 것에 비해 확연히 떨어진 것을 알 수 있습니다. 퍼센트로는 단순히 1%의 차이지만, 실제 학습 성능은 40%나 향상된 것입니다.

다만 실제 학습에서 Leave one out을 사용하기는 조금 곤란합니다. 데이터의 수가 매우 많을 때는 Cross Validation을 계산하는 시간이 너무 많이 걸리기 때문입니다. 그 때문에 실제로는 1개의 데이터만을 빼기 보단 몇 개의 데이터를 그룹화합니다.

많이 사용하는 방법 중에 10-fold Cross Validation이라는 것이 있습니다. 이 방법은 전체의 데이터를 10등분하여 Validation을 10번 계산하여 평균을 내는 방법입니다. 비록 Leave one out보다 $g$와 $g^{-}$의 Out of Sample Error 차이는 더 벌어지겠지만, 계산의 편의를 위해 이 방법이 더 권장된다고 합니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.