Eligibility Trace

이번 장에서 새로 배우는 Eligibility Trace는 강화학습의 기본 메커니즘 중 하나입니다. 예를 들어, TD($\lambda$)에서 $\lambda$는 Eligibility Trace를 사용한다는 것을 의미합니다. Q-learning과 Sarsa를 포함한 대부분의 TD 방법은 Eligibility Trace와 결합하여 보다 효율적으로 학습할 수 있습니다.

Eligibility Trace는 TD와 Monte Carlo Method를 통합하여 일반화하는 방법입니다. TD 방법을 Eligibility Trace를 사용하여 일반화하면 $\lambda = 1$일 때 Monte Carlo Method처럼 동작하며, $\lambda = 0$일 때 1-step TD로 동작합니다. 이로 인해 Eligibility Trace는 온라인으로 Monte Carlo Method을 구현할 수 있고, Episode가 없는 Continuing Problem에 대한 학습 방법을 구현할 수 있습니다.

Eligibility Trace의 메커니즘을 간단히 설명하자면, Eligibility Trace의 Short-term Memory Vector $\mathbf{z}_t \in \mathbb{R}^d$는 Long-term Weight Vector $\mathbf{w}_t \in \mathbb{R}^d$와 평행합니다. $\mathbf{w}_t$를 통해 함수를 추정할 때, $\mathbf{z}_t$의 구성 요소와 충돌한 후, $\mathbf{z}_t$는 사라지기 시작합니다. 이 Trace가 0으로 감소하기 전에 0이 아닌 TD Error가 발생하면, $\mathbf{w}_t$의 해당 구성 요소에서 학습이 일어납니다. 이 때 $\lambda \in \left[ 0, 1 \right]$는 Trace가 얼마나 빨리 0으로 감소하는 지 나타내는 Trace-decay Parameter입니다.

그런데 우리는 이미 7장에서 Monte Carlo와 1-step TD를 조율한 $n$-step TD를 배웠습니다. 하지만 Eligibility Trace는 $n$-step TD에 비해 계산적으로 이점이 있습니다. $n$-step TD는 마지막 $n$개의 Feature Vector를 저장했지만, Eligibility Trace는 1개의 Trace Vector만 필요합니다. 또한 $n$-step TD에서의 학습은 Episode가 끝나기 전까지 지연되는 방식이지만, Eligibility Trace는 지속적이고 균일하게 학습이 일어납니다.

Eligibility Trace를 통해 학습 알고리즘은 계산상의 이점을 위해 때때로 다른 방법으로 구현될 수도 있다는 것을 보여줍니다. 기존 방법을 예로 들자면, Monte Carlo Method와 $n$-step TD는 Episode의 마지막부터 Episode의 처음까지 학습하거나, $n$-step만큼 학습하였습니다. 이것을 Forward View라고 하는데, Forward View는 막상 알고리즘을 수행할 때 바로 사용할 수 없는 미래의 요소에 의존하기 때문에 구현하는 것이 상당히 복잡합니다. 그러나 Eligibility Trace는 알고리즘이 수행하는 순서와 거의 동일한 Update를 구현할 수 있습니다. 이것을 Backward View라고 합니다. 이번 장에서 이것에 대해 조금 더 자세히 다룰 예정입니다.

이번 장 역시 이전 장들과 마찬가지로, State-Value의 Prediction에 대한 개념을 먼저 다룬 다음에, Action-Value 및 Control 문제로 확장합니다. 또한 마찬가지로 On-policy 학습을 먼저, Off-policy 학습을 나중에 다룰 예정입니다. Function Approximation은 Linear Function Approximation에 중점을 둘 것이며, Tabular 방법과 State Aggregation 경우에도 적용할 수 있다는 것을 보일 예정입니다.

The $\lambda$-Return

먼저 7장에서 배운 $n$-step Return을 복습해봅시다. 식 (7.1)에서 $n$-step Return은 처음 $n$개의 Discounted Reward와 방문한 State의 Estimated Value의 합으로 정의했습니다. 이 식을 매개변수를 사용한 Function Approximation 식으로 수정하면 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n \hat{v} \left( S_{t+n}, \mathbf{w}_{t+n-1} \right), \quad 0 \le t \le T-n \tag{12.1}\]

식 (12.1)에서 $\hat{v} \left( s, \mathbf{w} \right)$는 Weight Vector $\mathbf{w}$가 주어졌을 때 State $s$의 근사값이고, $T$는 Episode가 종료되는 시간입니다.

또한 이러한 Update는 $n$-step Return 뿐만 아니라 다른 모든 $n$에 대한 $n$-step Return의 평균에 대해서도 유효합니다. 예를 들자면, 2-step Return의 절반과 4-step Return의 절반의 합으로 구성된 $\frac{1}{2} G_{t:t+2} + \frac{1}{2} G_{t:t+4}$와 같은 식에 대해서도 Update를 수행할 수 있다는 것입니다. 이렇게 각 Return의 Weight가 양수이면서 합이 1인 조건 하에서는 모든 $n$-step Return이 이런 방식으로 평균을 낼 수 있습니다. 심지어 항의 개수가 무한해도 말입니다. 이러한 평균화 기법을 이용하면 새로운 알고리즘을 개발할 수 있습니다. 예를 들어, TD나 Monte Carlo Method를 연결하기 위해 1-step 및 무한 단계 Return을 평균화하는 식으로 말입니다. 이와 같이 간단하게 구성 요소를 Update 하는 평균화 기법을 Compound Update 라고 합니다. 이에 대한 Backup Diagram은 Update 식에 따라 달라지는데, 방금 다룬 2-step Return의 절반과 4-step Return의 절반을 합친 식에 대한 Backup Diagram은 다음과 같습니다.

Backup Diagram에서 볼 수 있듯이, Compound Update의 Update를 수행하기 위해서는 가장 긴 구성 요소의 Update가 완료되어야 수행할 수 있습니다. 예를 들어, 위의 Backup Diagram에서 가장 긴 구성 요소는 4-step Return이므로, 시간 $t$에서의 추정치는 시간 $t+4$에 도달해야만 추정이 가능합니다. 이러한 문제로 인해 Update에 지연이 발생할 수 있으므로, 일반적으로는 가장 긴 구성 요소의 길이를 제한하는 방식으로 해결합니다.

$n$-step update를 평균화하는 방법 중 대표적으로 TD($\lambda$)가 있습니다. 이 방법은 모든 $n$-step update에 대해 $\lambda^{n-1}$의 Weight를 부여한 평균화 방법입니다. 그리고 이 Weight의 합을 1로 만들기 위해 맨 앞에 $1 - \lambda$를 곱해줍니다. 이것을 식으로 표현하면 다음과 같습니다.

\[G_t^{\lambda} \doteq (1 - \lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t:t+n} \tag{12.2}\]

식 (12.2)의 Update 식을 $\lambda$-Return 이라고 합니다. $\lambda$-Return의 Backup Diagram은 다음과 같이 표현할 수 있습니다.

$\lambda$-Return에서는 각 항의 계수가 다르기 때문에 Weight 또한 항 마다 다릅니다. 예를 들어, 1-step Return의 계수는 $(1 - \lambda)$이지만, 2-step Return은 $(1 - \lambda) \lambda$의 계수를 갖습니다. 이렇게 시간 $t$를 기준으로 멀어질수록 $\lambda$를 곱하기 때문에 Weight가 낮아집니다. 이것을 그림으로 표현하면 다음과 같습니다.

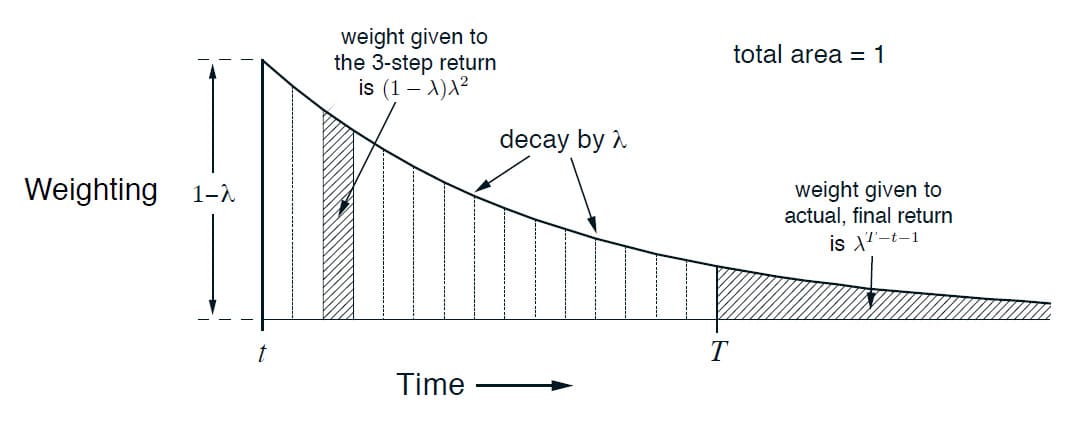
그림에서 보시다피시 마지막 항의 계수만 다른 항과 표현 방식이 다르기 때문에, 식 (12.2)를 다음과 같이 마지막 항만 분리하여 표현할 수도 있습니다.

\[G_t^{\lambda} = (1 - \lambda) \sum_{n=1}^{T-t-1} \lambda^{n-1} G_{t:t+n} + \lambda^{T-t-1}G_t \tag{12.3}\]

식 (12.3)에서 $\lambda = 1$인 경우를 따져봅시다. $(1 - \lambda)$ 항이 0이 되므로 2번째 항만 살아남아 Monte Carlo Return이 됩니다. 반대로 $\lambda = 0$인 경우라면 2번째 항이 사라짐은 물론, 1번째 항의 첫 번째 Return을 제외하고 모두 0이 되기 때문에 1-step Return이 됩니다. 따라서 $\lambda = 0$인 경우라면 $\lambda$-Return은 1-step TD 방법이 된다는 것을 알 수 있습니다.

이제 $\lambda$-Return을 기반으로 만든 첫 번째 학습 알고리즘인 Off-line $\lambda$-Return Algorithm을 소개하겠습니다. Off-line Algorithm이므로 Episode가 수행되는 동안에는 Weight Vector가 변경되지 않습니다. 그 후 Episode가 끝날 때 $\lambda$-Return을 Target으로 사용하여 일반적인 Semi-gradient Rule에 따라 Off-line Update의 전체 과정을 만들 수 있습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ G_t^{\lambda} - \hat{v} (S_t, \mathbf{w}) \right] \nabla \hat{v} (S_t, \mathbf{w}), \quad t = 0, \ldots, T - 1 \tag{12.4}\]

$\lambda$-Return은 7장에서 배웠던 $n$-step bootstrapping 방법과 다른 방법으로 Monte Carlo와 1-step TD 사이를 조절할 수 있는 대안을 제시합니다. 이에 대한 예시로 교재에서는 Random Walk Example을 제시하는데, 이 예제를 제가 7장에서 소개하지 않았습니다. 일단 여기에서 비교 내용만 설명하고, 추후 7장에 이 예제를 추가하겠습니다.

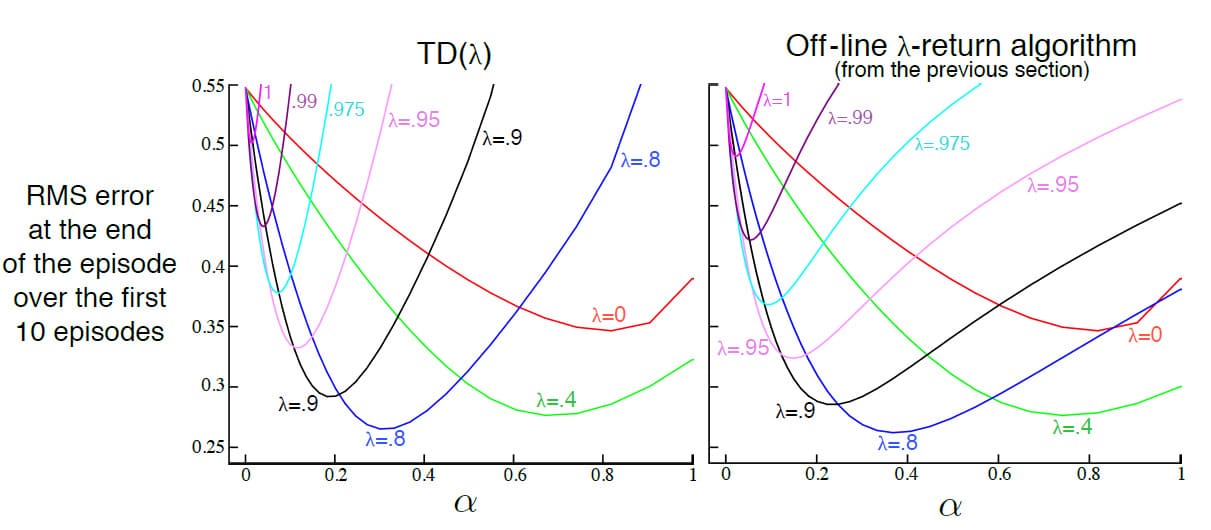
아래 그림은 19개의 State를 가진 Random Walk Example에서의 $\lambda$-Return Algorithm과 $n$-step TD 방법 비교 그래프입니다. 두 방법 모두 처음 10개의 Episode에 대한 평균을 나타내며 그래프의 세로축은 Root Mean Square Error를 의미하기 때문에 낮을 수록 좋습니다. 그래프를 보면 두 방법 모두 성능이 비슷하며, 중간 정도의 $\lambda$와 $n$일 때 최적의 성능을 보임을 알 수 있습니다.

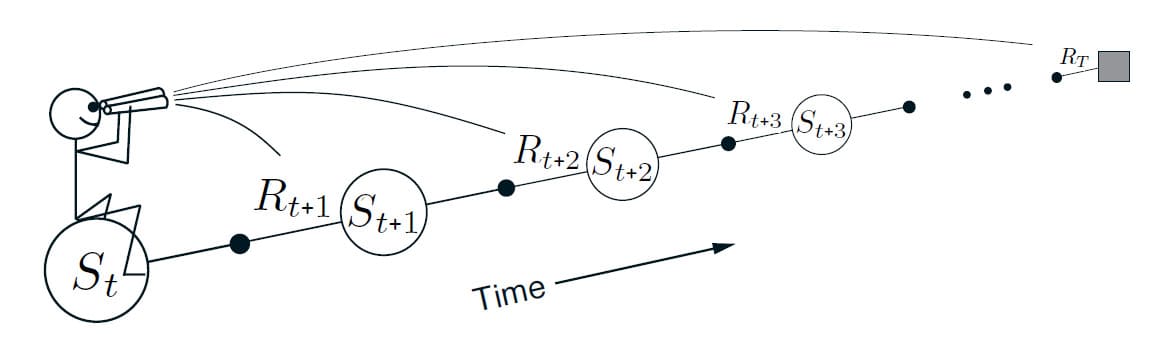
우리가 지금까지 취한 접근 방식은 학습 알고리즘에 대한 Theoretical View, 혹은 Forward View라고 부를 수 있습니다. 방문하는 각 State에 대해 향후 얻을 수 있는 모든 Reward에 대한 기대값과 이를 결합하는 최선의 방법을 결정하기 때문입니다. 아래 그림과 같이 Update를 결정하기 위해 각 State에서 기다리면서 State의 흐름을 타고 있다고 볼 수 있습니다. 한 State를 Update 한 후, 다음 State로 이동한 후에는 이 작업을 반복할 필요가 없습니다. 반면에 미래 State는 이전의 유리한 지점에서 한 번씩 반복적으로 처리됩니다.

TD($\lambda$)

TD($\lambda$)는 강화학습에서 가장 오래되고 널리 사용되는 알고리즘 중 하나입니다. TD($\lambda$)는 Eligibility Trace를 사용하여 Forward View와 Backward View 사이의 형식적인 관계를 나타내는 최초의 알고리즘입니다. Forward View는 이론적인 면에서, Backward View는 계산적인 면에서 각각 이점이 있습니다. 이번 Section에서는 TD($\lambda$)가 이전 Section에서 배운 Off-line $\lambda$-Return Algorithm에 근접함을 경험적으로 보여줄 것입니다.

TD($\lambda$)는 Off-line Return Algorithm을 세 가지 방식으로 개선합니다. 첫째, Episode가 끝날 때 뿐만 아니라 Episode의 모든 단계에서 Weight Vector를 Update함으로써 추정치를 더 빠르게 계산합니다. 둘째, Episode가 끝낼 때 한번에 계산하지 않고, 시간에 따라 계산이 균등하게 분산됩니다. 셋째, Episodic Task 뿐만 아니라 Continuing Task에도 적용할 수 있습니다. 이번 Section에서는 Function Approximation을 사용하여 TD($\lambda$)의 Semi-gradient 버전을 제시합니다.

Function Approximation에서 Eligibility Trace는 Weight Vector $\mathbf{w}_t$와 동일한 수의 구성 요소를 갖는 Vector $\mathbf{z}_t \in \mathbb{R}^d$입니다. Weight Vector는 시스템의 전체 수명 동안 누적되는 Long-term Memory이지만, Eligibility Trace는 일반적으로 Episode의 길이보다 짧은 시간 동안만 지속되는 Short-term Memory입니다. Eligibility Trace의 결과는 Weight Vector에 영향을 미치고 Weight Vector가 추정한 값을 결정함으로써 학습 과정에 도움이 됩니다.

TD($\lambda$)에서 Eligibility Trace의 Vector는 Episode 시작 시 Zero Vector로 초기화되고, 각 시간 단계에서 이전 Vector의 $\gamma \lambda$만큼 감소한 후, Value Function의 Gradient만큼 증가합니다. 이것을 수식으로 표현하면 다음과 같습니다.

\[\begin{align} \mathbf{z}_{-1} & \doteq \mathbf{0} \\ \\ \mathbf{z}_t & \doteq  \gamma \lambda \mathbf{z}_{t-1} + \nabla \hat{v} (S_t, \mathbf{w}_t), \quad 0 \le t \le T \tag{12.5} \end{align}\]

식 (12.5)에서 $\gamma$는 Discount Factor이고, $\lambda$는 이전 Section에서 소개한 매개변수인데, 앞으로 이것을 Trace-decay 매개변수라고 부르겠습니다. Eligibility Trace는 Weight Vector의 어떤 구성 요소가 최근 State에 대한 평가에 긍정적으로/부정적으로 기여했는지 Trace합니다. 여기서 최근은 $\gamma \lambda$로 정의됩니다. Trace는 학습 이벤트가 발생할 경우 그것에 의해 변경이 일어날 수 있는 Weight Vector에서 각 구성 요소들의 Eligibility를 나타냅니다. 여기서 우리가 우려할 수 있는 학습 이벤트는 매 순간의 1-step TD Error입니다. State-Value Prediction에 대한 TD Error는 다음과 같습니다.

\[\delta_t \doteq R_{t+1} + \gamma \hat{v} (S_{t+1}, \mathbf{w}_t) - \hat{v} (S_t, \mathbf{w}_t) \tag{12.6}\]

TD($\lambda$)에서 Weight Vector는 Scalar TD Error 및 Vector에 대한 Eligibility Trace에 비례하여 각 단계에서 다음과 같이 Update됩니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t \tag{12.7}\]

Semi-gradient TD($\lambda$)의 전체 Pseudocode는 다음과 같습니다.

TD($\lambda$)는 시간적으로 Backward View라고 볼 수 있습니다. 매 순간 현재의 TD Error를 확인하고, 그 State가 당시 Eligibility Trace에 얼마나 기여했는지에 따라 각각의 이전 State에 거꾸로 반영합니다. State가 미래에 다시 발생할 때를 대비하여 아래 그림과 같이 State의 흐름과 TD Error를 계산하고 식 (12.7)에 의해 얻은 Update를 이용하여 과거의 Value를 변경합니다.

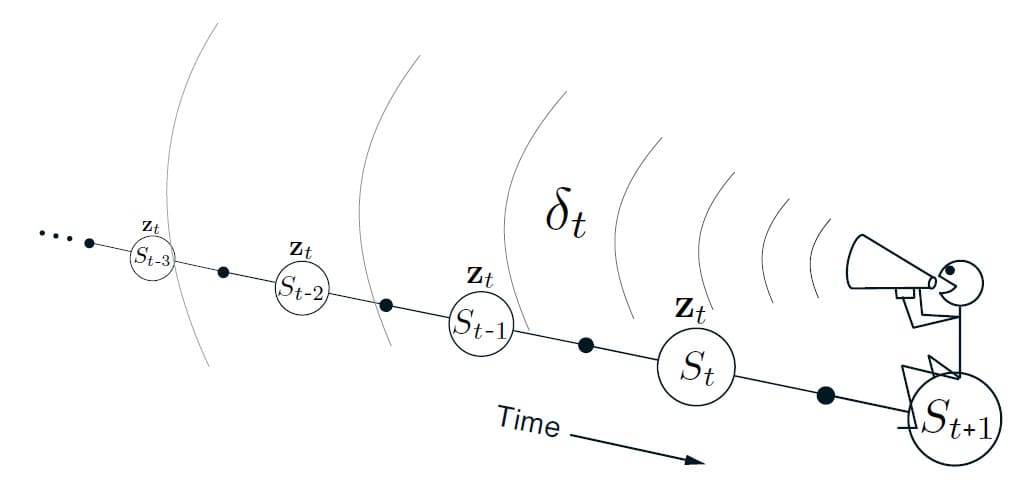
이것을 조금 더 잘 이해하기 위해서는 $\lambda$에 값에 따라 어떻게 달라지는지 생각해보면 됩니다. 만약 $\lambda = 0$인 경우라면 식 (12.5)에 의해 시간 $t$ 에서의 Trace는 정확히 State $S_t$에서 Value의 Gradient와 같습니다. 따라서 이 때의 TD($\lambda$) Update인 식 (12.7)은 9장에서 배운 1-step TD Update와 동일합니다. 이것이 그 당시 1-step TD Update를 TD(0)로도 불렀던 이유입니다. 위의 그림을 토대로 설명하자면, TD(0)는 현재 State를 기준으로 한 단계 이전의 State에 대한 TD Error로만 Update하는 경우입니다. 하지만 만약 $\lambda < 1$ 조건 하에 $\lambda$의 값이 증가한다면 더 많은 이전 State들이 Update되는데, 그림에서 볼 수 있듯이 시간적으로 멀리 떨어진 State일수록 Eligibility Trace가 더 작기 때문에 덜 Update됩니다. 이것을 초기 State는 TD Error에 대해 더 적은 Credit을 받았다라고 표현하기도 합니다.

만약 $\lambda = 1$인 경우라면, 이전 State에 부여된 Credit은 단계당 $\gamma$만큼 떨어집니다. 예를 들어, TD Error $\delta_t$는 Discount 되지 않은 $R_{t+1}$를 포함합니다. 그리고 이전의 $k$ 단계에 대한 Return을 계산할 때는 Reward에 $\gamma^k$ 만큼의 Discount가 곱해지는데, 이것은 점점 감소하는 Eligibility Trace가 됩니다. 만약 $\lambda = 1$이고 $\gamma = 1$일 때는 시간적으로 아무리 떨어져 있더라도 Eligibility Trace가 소멸되지 않습니다. 이 경우에는 Discount가 없는 Episodic Task에 대한 Monte Carlo Method처럼 작동합니다. $\lambda = 1$인 경우 알고리즘을 TD(1)으로도 부릅니다.

TD(1)은 기존의 Monte Carlo Method를 더 일반적으로 구현한 방법입니다. 기존의 Monte Carlo Method는 Episodic Task에 한정되었지만, TD(1)은 Discounted Continuing Task에도 적용할 수 있습니다. 또한 TD(1)은 점진적으로, 온라인으로 수행할 수도 있습니다. Monte Carlo Method는 Episode가 끝날 때까지 아무것도 학습하지 못한다는 단점이 있지만, TD(1)는 Episode가 끝나지 않은 상황에서도 그 일부분을 $n$-step TD 방식으로 학습할 수 있다는 장점이 있습니다. 예를 들어, 만약 Episode 중 비정상적으로 좋거나 나쁜 일이 발생하면 TD(1)에 기반한 Control은 즉시 이전까지의 내용을 학습하고 Episode를 변경할 수 있습니다.

TD($\lambda$)가 Off-line $\lambda$-Return Algorithm을 근사하는데 얼마나 성능이 좋은지 알아보기 위해 또 다시 19개의 State를 가진 Random Walk Example을 놓고 비교해보겠습니다. 아래 그림을 보시면 그래프의 모양 자체는 차이가 있지만, $\lambda$의 값이 최적인 State에서는 거의 동일한 성능을 보임을 알 수 있습니다. 다만 $\lambda$가 최적보다 크게 선택되는 상황을 보면 TD($\lambda$)는 Off-line $\lambda$-Return Algorithm보다 성능이 더 나쁘다는 것을 알 수 있습니다. 일반적으로 최적의 State를 제외하고는 $\lambda$를 사용하지 않기 때문에 큰 문제는 아닙니다만, TD($\lambda$)가 더 불안정하다라고는 말할 수 있을 정도의 단점은 됩니다.

Linear TD($\lambda$)는 On-policy인 경우 조건 식 (2.7)에 따라 Step-size Parameter가 시간에 따라 감소한다면 수렴합니다. Section 9.4에서 다룬 바와 같이 수렴한다는 것은 Weight Vector의 최소 오차가 $\lambda$에 따른다는 것을 의미합니다. 식 (9.14)에서 배운 오차 한계식은 $\lambda$에 의해 일반화될 수 있습니다. 만약 Discounted Continuing Task라면, 다음과 같습니다.

\[\overline{\text{VE}}(\mathbf{w}_{\text{TD}}) \le \frac{1 - \gamma \lambda}{1 - \gamma} \min_{\mathbf{w}} \overline{\text{VE}}(\mathbf{w}) \tag{12.8}\]

즉, 점근적인 오차는 가능한 최소 오차의 $\frac{1 - \gamma \lambda}{1 - \gamma}$배를 넘지 않는 다는 뜻입니다. $\lambda$가 1에 가까워질수록 최소 오차에 가까워집니다. 이렇게 보면 $\lambda$를 1에 가깝게 잡는 것이 좋아보이지만, 실제로는 가장 좋지 않은 선택이 될 가능성이 높은데, 그 이유는 나중에 밝혀집니다.

$n$-step Truncated $\lambda$-Return Methods

Off-line $\lambda$-Return Algorithm은 중요하지만, Episode가 끝날 때까지 알 수 없는 $\lambda$-Return을 이용하기 때문에 효용이 제한적입니다. (식 12.2 참고) Continuing Task의 경우, $\lambda$-Return은 기술적으로 계산할 수 없기 때문에 임의적으로 큰 $n$에 대해 $n$-step Return에 의존합니다. 하지만 시간적으로 멀리 떨어진 Reward일수록 $\gamma \lambda$만큼의 비율로 계속 비중이 줄어들기 때문에, 이 경우 근사를 하기 위해서는 일정 Step 마다 구간을 나누는 것이 좋습니다. $n$-step Return은 누락된 Reward를 추정된 값으로 대체하는 개념을 가지고 있습니다.

Episode를 일정 구간인 $h$만큼 자르는 경우, 시간 $t$에 대한 Truncated $\lambda$-Return 식은 다음과 같이 정의할 수 있습니다.

\[G_{t:h}^{\lambda} \doteq (1 - \lambda) \sum_{n=1}^{h-t-1} \lambda^{n-1} G_{t:t+n} + \lambda^{h-t-1}G_{t:h}, \quad 0 \le t < h \le T \tag{12.9}\]

이 식은 $h$의 역할이 식 (12.3)에서 $T$의 역할과 동일함을 알 수 있습니다. 또 다른 차이점을 굳이 찾자면 두 번째 항의 $G_t$ 대신 $G_{t:h}$로 변경된 것 정도가 있고, 그 외에는 식 (12.3)과 동일합니다.

Truncated $\lambda$-Return은 7장에서의 $n$-step 방법과 유사한 $n$-step Return Algorithm을 즉시 생성하는 방식으로 구성됩니다. 이 때의 Update는 $n$-step 만큼 지연되고 처음 $n$-step만 고려되었지만, 이제는 모든 $k$-step ($1 \le k \le n$) Return이 포함됩니다. State-Value의 경우 이 알고리즘과 같은 종류를 Truncated TD($\lambda$), 또는 TTD($\lambda$)라고 부릅니다. 아래 그림의 복합적인 Backup Diagram은 가장 긴 구성 요소에 대한 Update가 항상 Episode의 끝까지 진행되는 것이 아니라 최대 $n$-step이라는 점을 명시하고 있습니다. 그 점을 제외한다면 이전에 보여드린 $\lambda$-Return의 Backup Diagram과 유사합니다.

TTD($\lambda$)에 대한 식은 다음과 같이 표현할 수 있습니다.

\[\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1} + \alpha \left[ G_{t:t+n}^{\lambda} - \hat{v} (S_t, \mathbf{w}_{t+n-1}) \right] \nabla \hat{v} (S_t, \mathbf{w}_{t+n-1}), \quad 0 \le t < T\]

이 알고리즘은 각 단계별 계산이 $n$으로 확장되지 않도록 효율적으로 구현할 수 있습니다. (즉, 시간 복잡도가 $n$에 비례하지 않도록) $n$-step TD 방법과 마찬가지로 각 Episode의 처음 $n-1$ 시간 단계에서는 Update가 수행되지 않으며, Episode가 종료 후 $n-1$에 대한 추가적인 Update가 수행됩니다. 효율적인 구현을 위해 $k$-step $\lambda$-Return은 다음과 같이 표현으로 수정할 수 있습니다.

\[G_{t:t+k}^{\lambda} = \hat{v} (S_t, \mathbf{w}_{t-1}) + \sum_{i=t}^{t+k-1} (\gamma \lambda)^{i-t} \delta_i ' \tag{12.10}\]

이 때, $\delta_i^{\prime} \doteq R_{t+1} + \gamma \hat{v} (S_{t+1}, \mathbf{w}_t) - \hat{v} (S_t, \mathbf{w}_{t-1})$입니다.

Redoing Updates: Online $\lambda$-Return Algorithm

Truncated TD($\lambda$)에서 Truncation Parameter $n$을 선택할 때는 Trade-off가 있습니다. Truncated TD($\lambda$)가 Off-line $\lambda$-Return Algorithm에 근접하기 위해서 $n$이 커야 하지만, Update가 더 빨리 이루어지기 위해서는 $n$이 작아야 합니다. 이런 상황에서 둘 다 포기하지 않는 방법은 있지만, 그만큼 계산 복잡도가 증가하는 문제가 있습니다. 이번 Section에서는 이 방법을 소개하겠습니다.

기본적인 아이디어는 새로운 데이터의 Increment를 얻을 때마다 현재 Episode의 시작 부분으로 되돌아가 모든 Update를 다시 실행하는 것입니다. 그러면 각 시간 단계에서 새로운 데이터를 고려할 수 있기 때문에 새 Update는 이전에 계산한 결과보다 더 나을 것이기 때문입니다. 즉, Update는 항상 최신 Horizon $h$를 사용하여 $n$-step Truncated $\lambda$-Return의 Target을 계산하는 것입니다. 각 Episode가 끝날 때마다 약간 더 긴 Horizon $h$를 사용하면 약간 더 나은 결과를 얻을 수 있습니다. 먼저, 식 (12.9)에서의 Truncated $\lambda$-Return은 다음과 같이 정의했었습니다.

\[G_{t:h}^{\lambda} \doteq (1 - \lambda) \sum_{n=1}^{h-t-1} \lambda^{n-1} G_{t:t+n} + \lambda^{h-t-1}G_{t:h}\]

계산 복잡도가 문제가 되지 않는 상황에서 이 Target을 이상적으로 사용할 수 있는 방법을 단계별로 살펴보겠습니다. 각각의 Episode는 이전 Episode의 끝에서 $\mathbf{w}_0$을 사용하여 시간 0에서의 추정으로 시작합니다. 데이터 Horizon이 시간 단계 1로 확장될 때 학습이 시작됩니다. Horizon 1까지의 데이터가 주어지면, 시간 단계 0에서의 추정 Target은 $R_1$과 추정치 $\hat{v}(S_1, \mathbf{w}_0)$의 Bootstrap을 포함한 1-step Return $G_{0:1}$입니다. 이것은 정확하게 $G_{0:1}^{\lambda}$이며, 위 식의 첫 번째 항의 합은 0으로 감소합니다. 그 후 이 Target Update를 사용하여 $\mathbf{w}_1$을 만듭니다. 그 두 데이터 Horizon을 시간 단계 2로 진행한 후, $R_2$, $S_2$를 얻을 수 있으므로 $S_0$의 더 나은 Update인 $G_{0:2}^{\lambda}$와 $S_1$의 Update인 $G_{1:2}^{\lambda}$를 계산할 수 있습니다. 이렇게 더 나아진 Target을 사용하여 $S_1$과 $S_2$를 다시 Update하고, Weight Update를 $\mathbf{w}_0$부터 시작하여 $\mathbf{w}_2$를 계산합니다. 데이터 Horizon이 시간 단계 3으로 넘어가면 이 과정을 또다시 반복하는 것입니다. 이렇게 새로운 데이터 Horizon을 얻을 때마다 Weight Update를 $\mathbf{w}_0$부터 다시 계산하여 Update를 수행합니다.

이러한 개념적인 알고리즘은 각각의 Horizon $h$에서 동일한 Episode에 대한 서로 다른 Weight Vector를 생성합니다. 이것을 명확하게 설명하기 위해서는 다른 Horizon에서 계산된 Weight Vector를 구별할 수 있어야 합니다. Horizon $h$까지의 과정에서 시간 $t$의 Value를 추정하는데 사용한 Weight를 $\mathbf{w}_t^h$라 합시다. 각 과정에서의 첫 번째 Weight Vector $\mathbf{w}_0^h$는 이전 Episode로부터 상속된 것이고 (모든 $h$에 대해 마찬가지), 각 과정의 마지막 Weight Vector $\mathbf{w}_h^h$는 알고리즘의 궁극적인 Weight Vector를 정의합니다. 마지막 Horizon $h = T$에서는 다음 Episode의 초기 Weight를 생성하기 위해 전달할 최종 Weight $\mathbf{w}_T^T$를 얻습니다. 이러한 과정을 $h = 3$까지 수식으로 표현하자면 다음과 같습니다.

\[\begin{align} h = 1 : \mathbf{w}_1^1 \doteq \mathbf{w}_0^1 + \alpha \left[ G_{0:1}^{\lambda} - \hat{v} (S_0, \mathbf{w}_0^1) \right] \nabla \hat{v} (S_0, \mathbf{w}_0^1) \\ \\ h = 2 : \mathbf{w}_1^2 \doteq \mathbf{w}_0^2 + \alpha \left[ G_{0:2}^{\lambda} - \hat{v} (S_0, \mathbf{w}_0^2) \right] \nabla \hat{v} (S_0, \mathbf{w}_0^2) \\ \\ \quad \mathbf{w}_2^2 \doteq \mathbf{w}_1^2 + \alpha \left[ G_{1:2}^{\lambda} - \hat{v} (S_1, \mathbf{w}_1^2) \right] \nabla \hat{v} (S_1, \mathbf{w}_1^2) \\ \\ h = 3 : \mathbf{w}_1^3 \doteq \mathbf{w}_0^3 + \alpha \left[ G_{0:3}^{\lambda} - \hat{v} (S_0, \mathbf{w}_0^3) \right] \nabla \hat{v} (S_0, \mathbf{w}_0^3) \\ \\ \quad \mathbf{w}_2^3 \doteq \mathbf{w}_1^3 + \alpha \left[ G_{1:3}^{\lambda} - \hat{v} (S_1, \mathbf{w}_1^3) \right] \nabla \hat{v} (S_1, \mathbf{w}_1^3) \\ \\ \quad \mathbf{w}_3^3 \doteq \mathbf{w}_2^3 + \alpha \left[ G_{2:3}^{\lambda} - \hat{v} (S_2, \mathbf{w}_2^3) \right] \nabla \hat{v} (S_2, \mathbf{w}_2^3) \end{align}\]

이것을 일반화하면 다음과 같은 수식을 만들 수 있습니다.

\[\mathbf{w}_{t+1}^h \doteq \mathbf{w}_t^h + \alpha \left[ G_{t:h}^{\lambda} - \hat{v} (S_t, \mathbf{w}_t^h) \right] \nabla \hat{v} (S_t, \mathbf{w}_t^h), \quad 0 \le t < h \le T\]

만약 $\mathbf{w}_t \doteq \mathbf{w}_t^t$로 정의된다면 On-line $\lambda$-Return Algorithm이라고 부릅니다.

On-line $\lambda$-Return Algorithm은 완전하게 On-line으로 동작하며, 시간 $t$에서 사용할 수 있는 정보만 사용하여 새로운 Weight Vector $\mathbf{w}_t$를 계산합니다. 이 때의 단점은 매 시간 단계마다 경험한 Episode의 일부를 사용하여 계산하는 것이 계산 복잡도가 높다는 것입니다. Off-line $\lambda$-Return Algorithm은 Episode를 수행하는 동안 Update를 수행하지 않고, Episode를 종료하는 시점에서 모든 시간 단계에 대한 Update를 수행했기 때문에 계산 복잡도가 높지 않았습니다. On-line $\lambda$-Return Algorithm은 그 계산 복잡도를 대가로 Episode가 진행되는 도중 뿐만 아니라 Episode가 끝날 때도 더 나은 성능을 기대할 수 있습니다. Bootrstrapping에 사용되는 Weight Vector에 반영되는 정보가 더 많기 때문입니다. 아래 그림은 지금까지 보았던 Random Walk Example에서 On-line과 Off-line 알고리즘을 비교한 그래프입니다.

True Online TD($\lambda$)

이전 Section에서 제시한 On-line $\lambda$-Return Algorithm은 현재 가장 성능이 좋은 시분할 알고리즘입니다. 즉, On-line TD($\lambda$)를 근사화하는 이상적인 알고리즘입니다. On-line $\lambda$-Return Algorithm은 Forward View Algorithm이지만, 효율적으로 구현하기 위해서 Backward View Algorithm으로 변형시킬 방법이 있을까요? Linear Function Approximation의 경우라면 그 대답은 Yes입니다. 이 구현은 TD($\lambda$) Algorithm보다 On-line $\lambda$-Return Algorithm에 이상적으로 가깝기 때문에 True On-line TD($\lambda$) Algorithm이라고 합니다.

True On-line TD($\lambda$)를 유도하는 과정을 여기에서 보이기에는 너무 복잡하기 때문에 여기에서는 생략하겠습니다. (다음 Section 및 van Seijen et al., 2016) 대략적인 아이디어를 소개하자면, 먼저 On-line $\lambda$-Return Algorithm은 다음과 같이 삼각형으로 나열할 수 있습니다.

이 삼각형에서 하나의 행은 각 시간 단계에서 생성됩니다. 삼각형을 구성하는 요소는 많지만, 이전 Section에서 보았듯이 우리에게 필요한 것은 대각선 요소인 $\mathbf{w}_t^t$뿐입니다. 첫 번째 요소인 $\mathbf{w}_0^0$는 Episode의 초기 Weight Vector이고, 마지막 요소인 $\mathbf{w}_T^T$는 최종 Weight Vector이며, 그 중간 요소인 $\mathbf{w}_t^t$는 Update에 필요한 $n$-step Return을 얻기 위한 Bootstrapping 역할을 합니다.

이제 삼각형의 대각선 구성 요소(가장 오른쪽 요소)는 표기의 편의를 위해 $\mathbf{w}_t \doteq \mathbf{w}_t^t$로 재정의하겠습니다. 이제 해야할 것은 대각선 구성 요소인 $\mathbf{w}_t$를 간결하고 효율적으로 계산하는 방법을 찾는 것입니다. 그렇게 하면 $\hat{v}(\mathbf{s}, \mathbf{w}) = \mathbf{w}^{\sf T} \mathbf{x} (\mathbf{s})$와 같은 Linear에 대해 다음과 같은 True On-line TD($\lambda$) Algorithm을 만들 수 있습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t + \alpha \left( \mathbf{w}_t^{\sf T} \mathbf{w}_t - \mathbf{w}_{t-1}^{\sf T} \mathbf{x}_t \right) \left( \mathbf{z}_t - \mathbf{x}_t \right),\]

위 식에서 $\mathbf{x}_t \doteq \mathbf{x} (S_t)$이며, $\delta_t$는 TD($\lambda$)인 식 (12.6)을 의미합니다. 또한 $\mathbf{z}_t$는 다음과 같이 정의됩니다.

\[\mathbf{z}_t \doteq \gamma \lambda \mathbf{z}_{t-1} + \left( 1 - \alpha \gamma \lambda \mathbf{z}_{t-1}^{\sf T} \mathbf{x}_t \right) \mathbf{x}_t \tag{12.11}\]

이 알고리즘은 On-line $\lambda$-Return Algorithm과 정확하게 동일한 Weight Vector $\mathbf{w}_t (0 \le t \le T)$를 생성하는 것으로 증명되었습니다. (van Seijen et al., 2016) 이전 Section에서의 마지막 그림인 Random Walk의 On-line $\lambda$-Return Algorithm도 이것을 사용한 결과입니다. 이제 지금까지 단점으로 남아있던 높은 계산 복잡도가 해결되었습니다. 공간 복잡도 측면에서 보면 On-line TD($\lambda$)의 메모리 요구량은 기존 TD($\lambda$)의 메모리 요구량과 동일하고, 시간 복잡도 측면에서 보면 각 단계별 계산량은 약 50% 증가했지만, 전체적으로 보았을 때 각 단계별 시간 복잡도는 TD($\lambda$)와 동일하게 $O(d)$로 유지됩니다.

True On-line TD($\lambda$)의 전체 Pseudocode는 다음과 같습니다.

True On-line TD($\lambda$)에 사용된 Eligibility Trace 식 (12.11)은 기존의 TD($\lambda$)에서 사용한 Eligibility Trace 식 (12.5)와 구분하기 위해 Dutch Trace라고 부릅니다. 참고로 식 (12.5)와 같은 Eligibility Trace은 Accumulating Trace라고 부르기도 합니다.

이전에는 Tabular 방법이나 Tile Coding과 같은 Binary Feature Vector에 대해서는 Replacing Trace라고 하는 또 다른 방법을 사용했었습니다. Replacing Trace는 Feature Vector의 구성 요소가 1인지, 0인지에 따라 다르게 정의됩니다.

\[z_{i, t} \doteq \begin{cases} 1, & \text{if } x_{i, t} = 1 \\ \gamma \lambda z_{i, t-1}, & \text{otherwise} \end{cases} \tag{12.12}\]

요즘에는 Replacing Trace를 Dutch Trace의 조잡한 근사치 정도로 간주합니다. Replacing Trace는 일반적으로 Dutch Trace보다 성능이 낮기 때문에 Dutch Trace로 이를 대체하는 경우가 많습니다. 물론, 이에 대한 이론적인 근거 또한 있습니다. Accumulating Trace는 Dutch Trace를 사용할 수 없는 non-Linear Function Approximation에서 사용하기 때문에 중요한 Trace로 간주합니다.

Dutch Traces in Monte Carlo Learning

Eligibility Trace는 TD 학습과 밀접한 관련이 있는 것 같지만 실제로는 별로 관련이 없습니다. 이번 Section에서 보이겠지만, Monte Carlo 학습도 Eligibility Trace가 발생합니다. 9장에서 다루었던 Forward View에서 본 Linear Monte Carlo 알고리즘에 Dutch Trace를 사용하여 더 계산적으로 효율적인 Backward View 알고리즘을 유도할 수 있다는 것을 보일 예정입니다. 이점은 이 책의 저자가 인정하는 Forward View와 Backward View의 유일한 동치 부분입니다. 또한 이것은 True On-line TD($\lambda$)와 On-line $\lambda$-Return Algorithm의 동등성 증명 방향을 제공하지만, 훨씬 더 간단합니다.

먼저 Gradient Monte Carlo 예측 알고리즘의 Linear 버전은 Episode의 각 시간 단계에서 하나씩 다음과 같은 Update가 발생합니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ G - \mathbf{w}_t^{\sf T} \mathbf{x}_t \right] \mathbf{x}_t , \quad 0 \le t < T \tag{12.13}\]

예시를 단순화하기 위해 Return $G$는 Episode가 끝날 때 받은 단일 Reward이고 Discount가 없다고 가정합니다. (Return $G$는 단일 보상이기 때문에 $G_t$와 같이 시간에 대한 첨자가 붙지 않습니다.) 이 경우 Update는 Least Mean Square (LMS) 규칙이라고도 합니다. Monte Carlo 알고리즘에서의 모든 Update는 최종 Reward/Return에 따라 달라지므로 Episode가 끝날 때까지 아무것도 할 수 없기 때문에 Monte Carlo 알고리즘은 Off-line 알고리즘입니다. 그래서 여기서는 계산상의 이점이 있는 새로운 알고리즘의 구현을 목적으로 합니다. 새로운 알고리즘에서도 기존과 마찬가지로 Episode가 끝날 때만 Weight Vector를 Update하겠지만, Episode의 각 단계에서 약간의 계산을 수행함으로써 전체적으로 계산량을 고르게 분배할 계획입니다. 이것을 통해 단계당 $O(d)$의 시간 복잡도가 소요되지만, 각 단계에서 Feature Vector를 저장할 필요가 없습니다. 대신 Eligibility Trace를 도입하여 지금까지 경험한 모든 Feature Vector의 요점만을 저장합니다. 이 방법은 Episode가 끝날 때까지 식 (12.13)의 Update 과정과 정확히 동일한 Update를 효율적으로 재생성합니다. 식에 대한 전개 과정은 다음과 같습니다.

\[\begin{align} \mathbf{w}_{T} &= \mathbf{w}_{T-1} + \alpha \left( G - \mathbf{w}_{T-1}^{\sf T} \mathbf{x}_{T-1} \right) \mathbf{x}_{T-1} \\ \\ &= \mathbf{w}_{T-1} + \alpha \mathbf{x}_{T-1} \left( - \mathbf{x}_{T-1}^{\sf T} \mathbf{w}_{T-1} \right) + \alpha G \mathbf{x}_{T-1} \\ \\ &= \left( \mathbf{I} - \alpha \mathbf{x}_{T-1} \mathbf{x}_{T-1}^{\sf T} \right) \mathbf{w}_{T-1} + \alpha G \mathbf{x}_{T-1} \\ \\ &= \mathbf{F}_{T-1} \mathbf{w}_{T-1} + \alpha G \mathbf{x}_{T-1} \end{align}\]

이 때 $\mathbf{F}_{t} \doteq \mathbf{I} - \alpha \mathbf{x}_t \mathbf{x}_t^{\sf T}$는 Forgetting, 또는 Fading이라고 부르는 행렬입니다. 이제 위 식을 재귀적으로 전개해보면,

\[\begin{align} &= \mathbf{F}_{T-1} \left( \mathbf{F}_{T-2} \mathbf{w}_{T-2} + \alpha G \mathbf{x}_{T-2} \right) + \alpha G \mathbf{x}_{T-1} \\ \\ &= \mathbf{F}_{T-1} \mathbf{F}_{T-2} \mathbf{w}_{T-2} + \alpha G \left( \mathbf{F}_{T-1} \mathbf{x}_{T-2} + \mathbf{x}_{T-1} \right) \\ \\ &= \mathbf{F}_{T-1} \mathbf{F}_{T-2} \left( \mathbf{F}_{T-3} \mathbf{w}_{T-3} + \alpha G \mathbf{x}_{T-3} \right) + \alpha G \left( \mathbf{F}_{T-1} \mathbf{x}_{T-2} + \mathbf{x}_{T-1} \right) \\ \\ &= \mathbf{F}_{T-1} \mathbf{F}_{T-2} \mathbf{F}_{T-3} \mathbf{w}_{T-3} + \alpha \left( \mathbf{F}_{T-1} \mathbf{F}_{T-2} \mathbf{x}_{T-3} + \mathbf{F}_{T-1} \mathbf{x}_{T-2} + \mathbf{x}_{T-1} \right) \\ \\ & \qquad \qquad \vdots \\ \\ &= \underbrace{\mathbf{F}_{T-1} \mathbf{F}_{T-2} \cdots \mathbf{F}_0 \mathbf{w}_0}_{\mathbf{a}_{T-1}} + \alpha G \underbrace{\sum_{k=1}^{T-1} \mathbf{F}_{T-1} \mathbf{F}_{T-2} \cdots \mathbf{F}_{k+1} \mathbf{x}_k}_{\mathbf{z}_{T-1}} \\ \\ &= \mathbf{a}_{T-1} + \alpha G \mathbf{z}_{T-1} \tag{12.14} \end{align}\]

여기서 $\mathbf{a}_{T-1}$과 $\mathbf{z}_{T-1}$는 시간 $T-1$에서의 메모리 Vector로써, $G$에 대한 정보 없이 각 시간 단계에서 $O(d)$의 시간 복잡도로 Update할 수 있습니다. 이 중 Vector $\mathbf{z}_{t}$는 Dutch-style Eligibility Trace입니다. 이 Vector는 시간 단계 0에서 $\mathbf{z}_0 = \mathbf{x}_0$으로 초기화된 후 다음과 같이 Update됩니다.

\[\begin{align} \mathbf{z}_t & \doteq \sum_{k=1}^t \mathbf{F}_t \mathbf{F}_{t-1} \cdots \mathbf{F}_{k+1} \mathbf{x}_k, \quad 1 \le t < T \\ \\ &= \sum_{k=0}^{t-1} \mathbf{F}_t \mathbf{F}_{t-1} \cdots \mathbf{F}_{k+1} \mathbf{x}_k + \mathbf{x}_t \\ \\ &= \mathbf{F}_t \sum_{k=1}^{t-1} \mathbf{F}_{t-1} \mathbf{F}_{t-2} \cdots \mathbf{F}_{k+1} \mathbf{x}_k + \mathbf{x}_t \\ \\ &= \mathbf{F}_t \mathbf{z}_{t-1} + \mathbf{x}_t \\ \\ &= \left( I - \alpha \mathbf{x}_t \mathbf{x}_t^{\sf T} \right) \mathbf{z}_{t-1} + \mathbf{x}_t \\ \\ &= \mathbf{z}_{t-1} - \alpha \mathbf{x}_t \mathbf{x}_t^{\sf T} \mathbf{z}_{t-1} + \mathbf{x}_t \\ \\ &= \mathbf{z}_{t-1} - \alpha \left( \mathbf{z}_{t-1}^{\sf T} \mathbf{x}_t \right) \mathbf{x}_t + \mathbf{x}_t \\ \\ &= \mathbf{z}_{t-1} + \left( 1 - \alpha \mathbf{z}_{t-1}^{\sf T} \mathbf{x}_t \right) \mathbf{x}_t \end{align}\]

이것은 식 (12.11)에서 $\gamma \lambda = 1$인 경우에 대한 Dutch Trace입니다. Auxiliary Vector $\mathbf{a}_t$는 시간 단계 0에서 $\mathbf{a}_0 = \mathbf{w}_0$로 초기화 된 후, 다음과 같이 Update됩니다.

\[\mathbf{a}_t \doteq \mathbf{F}_t \mathbf{F}_{t-1} \cdots \mathbf{F}_0 \mathbf{w}_0 = \mathbf{F}_t \mathbf{a}_{t-1} = \mathbf{a}_{t-1} - \alpha \mathbf{x}_t \mathbf{x}_t^{\sf T} \mathbf{a}_{t-1}, \quad 1 \le t < T\]

Auxiliary Vector $\mathbf{a}_t$와 Dutch Trace $\mathbf{z}_{t}$는 각 시간 단계 $t < T$에서 Update되고 $G$를 알 수 있는 시간 단계 $T$에서는 $\mathbf{w}_T$를 계산하기 위해 식 (12.14)에서 사용됩니다. 이런 방법으로 계산 복잡도가 높은 식 (12.13)과 같은 MC/LMS 알고리즘과 정확히 동일한 최종 결과를 얻었습니다. 새로 구한 방법은 각 시간 단계별 시간 복잡도 및 공간 복잡도가 $O(d)$인 증분 알고리즘을 사용합니다. 이것은 TD Learning이 아닌 환경에서 Eligibility Trace의 개념이 발생했기 때문에 흥미로운 결과입니다. 그러므로 Eligibility Trace는 TD Learning에만 국한되지 않는다는 것을 알 수 있습니다. Eligibility Trace의 필요성은 효율적인 방식으로 장기적인 예상치를 학습하고자 할 때 나타나는 것으로 보면 될 것 같습니다.

Sarsa($\lambda$)

Eligibility Trace를 Action-Value로 확장하기 위해서는 다행스럽게도 이미 제시된 아이디어에서 거의 변경할 필요가 없습니다. Estimated Value인 $\hat{q} (s, a, \mathbf{w})$를 학습하기 위해서는 아래와 같이 10장에서 배운 $n$-step Return의 Action-Value 형태를 사용해야 합니다.

\[G_{t:t+n} \doteq R_{t+1} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n \hat{q} \left( S_{t+n}, A_{t+n}, \mathbf{w}_{t+n-1} \right), \quad t+n < T\]

이 때 만약 $t + n \ge T$인 경우라면 $G_{t:t+n} \doteq G_t$입니다. 이 방법을 통해 $\lambda$-Return의 Action-Value 형태를 만들 수 있습니다. Off-line $\lambda$-Return Algorithm의 Action-Value 형식은 단순히 $\hat{v}$를 $\hat{q}$로 대체하면 됩니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ G_t^{\lambda} - \hat{q} \left( S_t, A_t, \mathbf{w}_t \right) \right] \nabla \hat{q} \left( S_t, A_t, \mathbf{w}_t \right), \quad t = 0, \ldots, T - 1 \tag{12.15}\]

이 때 $G_t^{\lambda} \doteq G_{t:\infty}^{\lambda}$입니다. 이 Forward View 에 대한 복합적인 Backup Diagram은 다음과 같습니다.

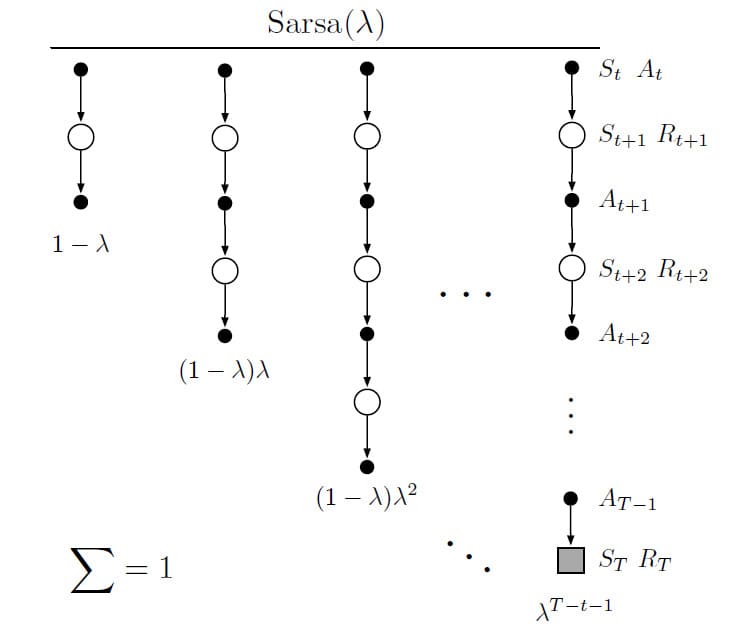
위의 Backup Diagram과 TD($\lambda$)의 Backup Diagram을 비교해보면 굉장히 유사하다는 것을 알 수 있습니다. 또한 $\lambda$-Return에서 각 $n$-step Update의 Weight는 TD($\lambda$) 및 $\lambda$-Return 알고리즘에서와 같습니다.

Action Value에 대한 TD 방법은 Sarsa($\lambda$)로 알려져 있는데, 이것은 이 Forward View를 추정합니다. 이 방법의 Update 규칙은 아래와 같이 TD($\lambda$)와 동일합니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t\]

단, TD Error의 Action-Value 형태는 예외적입니다.

\[\delta_t \doteq R_{t+1} + \gamma \hat{q} \left( S_{t+1}, A_{t+1}, \mathbf{w}_t \right) - \hat{q} \left( S_t, A_t, \mathbf{w}_t \right) \tag{12.16}\]

또한 Eligibility Trace의 Action-Value 형태는 다음과 같습니다.

\[\begin{align} \mathbf{z}_{-1} & \doteq \mathbf{0} \\ \\ \mathbf{z} & \doteq \gamma \lambda \mathbf{z}_{t-1} + \nabla \hat{q} \left( S_t, A_t, \mathbf{w} \right), \quad 0 \le t \le T \end{align}\]

Sarsa($\lambda$)의 완전한 Pseudocode는 다음과 같습니다.

Example 12.1) Traces in Gridworld

Eligibility Trace를 사용하면 1-step 방법이나 $n$-step 방법보다 Control 알고리즘의 효율성을 크게 높일 수 있습니다. Gridworld 예제를 이용하여 이것을 설명하겠습니다.

첫 번째 그림은 단일 Episode에서 Agent가 이동한 경로를 나타냅니다. 초기 Estimated Value는 0이고, G로 표시된 Target 지점을 제외하면 모든 Reward는 0입니다. 나머지 그림에 나타난 화살표는 각각의 알고리즘에 대해 어떤 Action-Value가 얼마나 증가하는지를 나타냅니다. 1-step Sarsa는 Target에 도달했을 때 마지막 Action에 대한 Value만 증가시키지만, $n$-step 방법은 마지막 $n$개의 Action에 대한 Value를 동일하게 증가시킵니다. ($\gamma = 1$이라고 가정) 가장 오른쪽에 있는 Sarsa($\lambda$) 방법은 Episode에서의 모든 Action에 대한 Value를 Update 하지만, Target 지점에서 (시간적으로) 멀어질수록 더 적게 반영됩니다. 이러한 Update 방법을 Fading이라고 하는데, 일반적으로 Fading 방법이 제일 좋은 경우가 많습니다.

□

Example 12.2) Sarsa($\lambda$) on Mountain Car

이번에는 10장에서 다루었던 Mountain Car 예제에 Sarsa($\lambda$)를 적용해 보겠습니다. 기본적인 예제의 세팅은 10장에서와 동일합니다. 위의 그림은 Mountain Car 문제에 대해  Sarsa($\lambda$)와 $n$-step Sarsa의 성능을 비교한 그래프입니다. $n$-step Sarsa에서는 변수로써 $n$의 값을 변경하며 비교했지만, Sarsa($\lambda$)에서는 $\lambda$의 값을 변경하며 비교합니다. 두 그래프를 비교해보면 Sarsa($\lambda$)의 Fading-trace bootstrapping 전략이 이 문제에 대해 더 효율적인 학습 방법이라는 것을 알 수 있습니다.

□

또한 이상적인 TD 방법의 Action-Value 버전을 On-line $\lambda$-Return 알고리즘 및 True On-line TD($\lambda$)으로 구현할 수도 있습니다. Section 12.4에서 다룬 On-line $\lambda$-Return 알고리즘의 Action-Value 버전은 $n$-step Return을 Action-Value 형식으로 바꾸는 것 외에는 변경할 부분이 없습니다. 또한 Section 12.5와 12.6에서의 분석은 Action-Value에 대해서도 동일하며, 유일한 차이점은 State에 대한 Feature Vector를 $\mathbf{x}_t = \mathbf{x}(S_t)$ 대신 $\mathbf{x}_t = \mathbf{x}(S_t, A_t)$로 사용한다는 것입니다. True On-line Sarsa($\lambda$)에 대한 전체 Pseudocode는 다음과 같습니다.

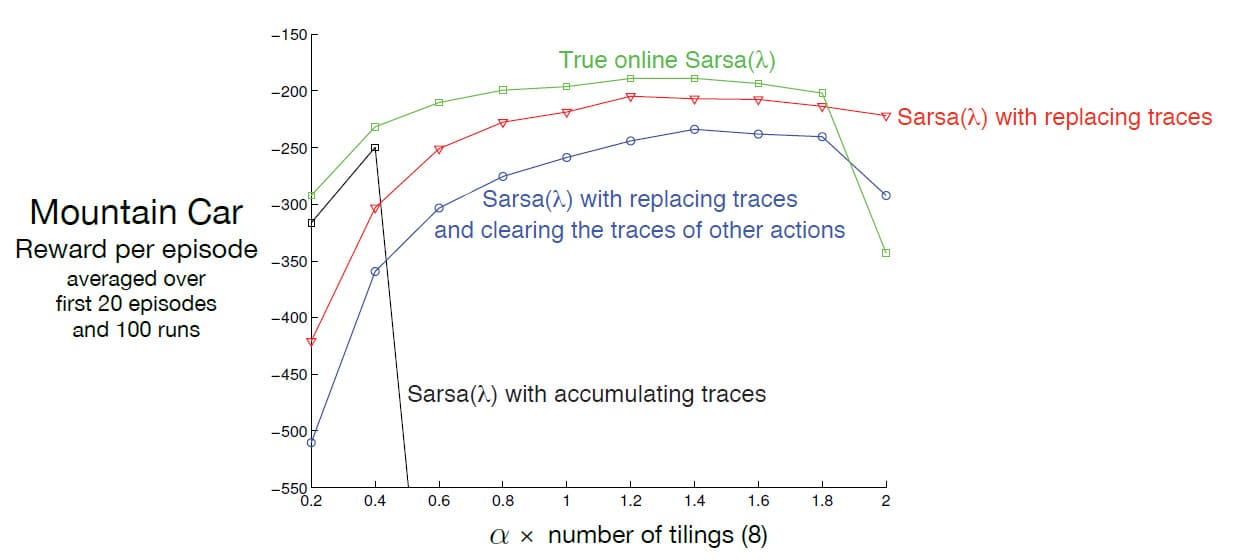
아래 그림은 Mountain Car 예제에서 Sarsa($\lambda$)의 여러 버전에 대해 성능을 비교하는 그래프입니다. True On-line Sarsa($\lambda$)는 일반 Sarsa($\lambda$)보다 더 나은 성능을 보여줌을 알 수 있습니다.

Variable $\lambda$ and $\gamma$

이제 기본적인 TD Learning 알고리즘에 대한 개발은 끝을 향해 달려가고 있습니다. 최종 알고리즘을 일반적인 형태로 나타내기 위해서는 State와 Action에 잠재적으로 의존하는 함수에 대해 일정한 매개변수는 물론, Bootstrapping 및 Discounting에 대한 정도를 일반화하는 것이 좋습니다. 즉, 각 시간 단계에 대해 서로 다른 $\lambda$및 $\gamma$를 설정하여, 이것을 각각 $\lambda_t$와 $\gamma_t$로 표현하는 것입니다. 또한 표기법을 변경하여 기존의 $\lambda$는 $\lambda : \mathcal{S} \times \mathcal{A} \to [0, 1]$와 같이 State와 Action에 대한 함수로 정의하고, 시간에 따라 변하는 $\lambda_t$는 $\lambda_t \doteq \lambda (S_t, A_t)$와 같이 함수 $\lambda$를 사용하여 표현합니다. 비슷하게, $\gamma$ 또한 $\gamma : \mathcal{S} \to [0, 1]$로 정의하고, $\gamma_t$를 $\gamma_t \doteq \gamma (S_t)$로 표현합니다.

함수 $\gamma$는 특히 더 중요한데, 우리가 추정하고자 하는 기본 확률 변수인 Return을 변경하기 때문입니다. 이 함수 $\gamma$를 앞으로 Termination Function이라고 부르겠습니다. 이제 Return을 다음과 같이 더 일반적으로 정의하겠습니다.

\[\begin{align} G_t & \doteq R_{t+1} + \gamma_{t+1} G_{t+1} \\ \\ &= R_{t+1} + \gamma_{t+1} R_{t+2} + \gamma_{t+1} \gamma_{t+2} R_{t+3} + \gamma_{t+1} \gamma_{t+2} \gamma_{t+3} R_{t+4} + \cdots \\ \\ &= \sum_{k=t}^{\infty} \left( \prod_{i=t+1}^{k} \gamma_i \right) R_{k+1} \tag{12.17} \end{align}\]

식 (12.17)에서 합이 유한함을 보장하기 위해서는 모든 $t$에 대해 1의 확률로 $\prod_{k=t}^{\infty} \gamma_k = 0$를 만족해야 합니다.

위와 같은 정의의 편리한 점은 Episode의 설정이나 알고리즘이 특정한 Terminal State나 Start Distribution, 종료 시간과 같은 특별한 설정 없이 단일 경험의 관점에서 표시될 수 있다는 것입니다. 특별한 경우로, 이전의 Terminal State는 $\gamma (s) = 0$인 State가 되어 Start Distribution으로 전환됩니다. 그리고 다른 모든 State에서 상수로 $\gamma ( \cdot )$를 선택함으로써 고전적인 Episode Task로 설정할 수 있습니다. State에 의존적인 종료에는 Markov Process의 흐름을 변경하지 않고 수량을 예측하는 Pseudo Termination과 같은 다른 예측 사례가 포함됩니다. Discounted Return은 그러한 수량으로 생각할 수 있으며, 이 경우 State에 의존적인 종료는 Episodic Task과 Discounted-Continuing Task 모두를 통합합니다. 물론 unDiscounted-Continuing Task의 경우 여전히 특별한 해결 방법이 필요합니다. (이 문단의 번역이 굉장히 어렵네요. 최대한 노력했습니다만 이해가 어려우실 것 같아 원문을 함께 봐주시기 바랍니다)

가변 Bootsrtapping에 대한 일반화는 Discounting과 같은 문제의 변경이 아니라 해결 방법의 변경입니다. 일반화하는 State와 Action을 위한 $\lambda$-Return에 영향을 미칩니다. 새로운 State 기반 $\lambda$-Return은 다음과 같이 재귀적으로 작성할 수 있습니다.

\[G_t^{\lambda s} \doteq R_{t+1} + \gamma_{t+1} \left( (1 - \lambda_{t+1}) \hat{v} (S_{t+1}, \mathbf{w}_t) + \lambda_{t+1} G_{t+1}^{\lambda s} \right) \tag{12.18}\]

식 (12.18)은 위 첨자 $s$를 추가하여 이것이 State-Value에서 Bootstrapping 하는 Return임을 나타내고 있습니다. 이와 반대로 아래 식 (12.19)는 위 첨자로 $a$를 추가하여 Action-Value에서 Bootstrapping 하는 Return임을 나타냅니다. 이 식의 첫 번째 항은 $\lambda$-Return에서 Bootstrapping에 영향받지 않고 unDiscounted인 첫 번째 Reward를 의미합니다. 두 번째 항은 만약 다음 State가 Terminal State라면 0이 됩니다.

만약 다음 State가 Terminal State가 아니라면, 두 번째 항은 State의 Bootstrapping 정도에 따라 두 가지 경우로 구분됩니다. Bootstrapping하는 범위 내에서 이 항은 State에서 추정된 값이지만, Bootstrapping 하지 않는 범위에서 이 항은 다음 시간 단계에서의 $\lambda$-Return입니다.

Action 기반의 $\lambda$-Return Sarsa 형태는 다음과 같습니다.

\[G_t^{\lambda a} \doteq R_{t+1} + \gamma_{t+1} \left( (1 - \lambda_{t+1}) \hat{q} (S_{t+1}, A_{t+1}, \mathbf{w}_t) + \lambda_{t+1} G_{t+1}^{\lambda a} \right) \tag{12.19}\]

위 식을 Expected Sarsa 형태로 수정하면 다음과 같습니다.

\[G_t^{\lambda a} \doteq R_{t+1} + \gamma_{t+1} \left( (1 - \lambda_{t+1}) \bar{V}_t (S_{t+1}) + \lambda_{t+1} G_{t+1}^{\lambda a} \right) \tag{12.20}\]

식 (12.20)에서 $\bar{V}_t (s)$는 다음과 같이 Function Approximation으로 정의됩니다.

\[\bar{V}_t (s) \doteq \sum_a \pi (a | s) \hat{q} (s, a, \mathbf{w}_t) \tag{12.21}\]

Off-policy Traces with Control Variates

Eligibility Trace의 마지막 단계는 Importance Sampling을 통합하는 것입니다. non-Truncated $\lambda$-Return을 사용하는 방법의 경우 Importance Sampling의 Weight가 Target Return에 적용할 수 있는 옵션이 없습니다. (ex. Section 7.3의 $n$-step 방법) 그래서 대신 Section 7.4에서와 같이 Control Variate가 있는 Per-decision Importance Sampling의 Bootstrapping 일반화로 해결하고자 합니다.

State의 경우, 식 (12.18)의 $\lambda$-Return 일반화에 대한 최종 정의는 식 (7.13)과 결합하여 다음과 같이 정의됩니다.

\[G_t^{\lambda s} \doteq \rho_t \Big( R_{t+1} + \gamma_{t+1} \big( (1 - \lambda_{t+1}) \hat{v} (S_{t+1}, \mathbf{w}) + \lambda_{t+1} G_{t+1}^{\lambda s} \big) \Big) + (1 - \rho_t) \hat{v} (S_t, \mathbf{w}_t) \tag{12.22}\]

여기서 $\rho_t = \frac{\pi (A_t \mid S_t)}{b (A_t \mid S_t)}$는 단일 단계 Importance Sampling Ratio입니다. 이 교재에서 다루었던 다른 Return과 마찬가지로 이 최종 $\lambda$-Return은 단순히 State 기반 TD Error의 합계로 근사할 수 있습니다. 먼저 State 기반 TD Error는 다음과 같이 표현할 수 있습니다.

\[\delta_t^s \doteq R_{t+1} + \gamma_{t+1} \hat{v} (S_{t+1}, \mathbf{w}_t) - \hat{v}(S_t, \mathbf{w}_t) \tag{12.23}\]

이것을 통해 $G_t^{\lambda s}$를 근사하면,

\[G_t^{\lambda s} \approx \hat{v}(S_t, \mathbf{w}_t) + \rho_t \sum_{k=t}^{\infty} \delta_k^s \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \tag{12.24}\]

이 때, Approximate Value Function $\hat{v}$가 변하지 않으면 식 (12.24)의 근사는 정확해집니다.

식 (12.24)와 같은 $\lambda$-Return의 형태는 Forward-View Update에서 사용하기 편리해 보입니다.

\[\begin{align} \mathbf{w}_{t+1} &= \mathbf{w}_t + \alpha \big( G_t^{\lambda s} - \hat{v} (S_t, \mathbf{w}_t) \big) \nabla \hat{v} (S_t, \mathbf{w}_t) \\ \\ & \approx \mathbf{w}_t + \alpha \rho_t \left( \sum_{k=t}^{\infty} \delta_k^s \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \right) \nabla \hat{v} (S_t, \mathbf{w}_t) \end{align}\]

위 식은 Eligibility에 기반한 TD Update처럼 보입니다. $\prod$ 연산 부분은 Eligibility Trace와 같으며, 여기에 TD Error가 곱해집니다. 그러다 이것은 Forward View의 한 단계일 뿐입니다. 우리가 찾고 있는 관계는 시간이 지남에 따라 합산되는 Forward View Update가 역시 시간이 지남에 따라 합산되는 Backward View Update와 거의 같다는 것입니다. (다만 이 관계는 Value Function의 변경을 무시하기 때문에 대략적인 것으로만 성립합니다) 시간 경과에 따른 Forward View Update의 합계는 다음과 같습니다.

\[\begin{align} \sum_{t=0}^{\infty} (\mathbf{w}_{t+1} - \mathbf{w}_t) & \approx \sum_{t=0}^{\infty} \sum_{k=t}^{\infty} \alpha \rho_t \delta_k^s \nabla \hat{v} (S_t, \mathbf{w}_t) \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \\ \\ &= \sum_{k=0}^{\infty} \sum_{t=0}^k \alpha \rho_t \nabla \hat{v} (S_t, \mathbf{w}_t) \delta_k^s \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \\ \\ &(\text{using the summation rule : } \sum_{t=x}^y \sum_{k=t}^y = \sum_{k=x}^y \sum_{t=x}^k) \\ \\ &= \sum_{k=0}^{\infty} \alpha \delta_k^s \sum_{t=0}^k \rho_t \nabla (S_t, \mathbf{w}_t) \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \end{align}\]

위 식의 두 번째 합계부터는 전체 표현식이 Eligibility Trace으로 작성되고 점진적으로 Update 될 수 있는 경우 Backward View TD Update의 합계 형태가 될 것입니다. 즉, 이 표현식이 시간 $k$에서의 trace이면, 시간 $k-1$의 Value에서 이것을 Update할 수 있습니다.

\[\begin{align} \mathbf{z}_k &= \sum_{t=0}^k \rho_t \nabla \hat{v} (S_t, \mathbf{w}_t) \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \\ \\ &= \sum_{t=0}^{k-1} \rho_t \nabla \hat{v} (S_t, \mathbf{w}_t) \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i + \rho_k \nabla \hat{v}(S_k, \mathbf{w}_k) \\ \\ &= \gamma_k \lambda_k \rho_k \underbrace{\sum_{t=0}^{k-1} \rho_t \nabla \hat{v} (S_t, \mathbf{w}_t) \prod_{i=t+1}^{k-1} \gamma_i \lambda_i, \rho_i}_{\mathbf{z}_{k-1}} + \rho_k \nabla \hat{v} (S_k, \mathbf{w}_k) \\ \\ &= \rho_k \big( \gamma_k \lambda_k \mathbf{z}_{k-1} + \nabla \hat{v} (S_k, \mathbf{w}_k) \big) \end{align}\]

위 전개식에서는 아래 첨자가 $k$로 나와있지만, 시간에 대해 일반화하는 것을 명시하기 위해 아래 첨자를 $t$로 수정하여 최종 결과를 정리하겠습니다.

\[\mathbf{z}_t \doteq \rho_t \big( \gamma_t \lambda_t \mathbf{z}_{t-1} + \nabla \hat{v} (S_t, \mathbf{w}_t) \big) \tag{12.25}\]

이 Eligibility Trace는 식 (12.7)과 같은 TD($\lambda$)에 대한 일반적인 Semi-gradient 매개변수 Update 규칙과 함께 On-policy 또는 Off-policy 데이터에 적용할 수 있는 일반적인 TD($\lambda$) 알고리즘을 형성합니다. On-policy의 경우 $\rho_t$가 항상 1이므로 식 (12.25)가 식 (12.5)와 동일해지기 때문에 알고리즘은 정확히 TD($\lambda$)입니다. Off-policy의 경우 알고리즘이 잘 작동하는 경우가 많지만 Semi-gradient 방법으로는 안정성이 보장되지 않습니다. 이어지는 다음 여러 Section을 통해 안정성을 보장할 수 있는 방법을 고려할 것입니다.

위와 유사한 과정을 거쳐 Action-Value에 대한 방법과 이에 해당하는 일반적인 Sarsa($\lambda$) 알고리즘에 대한 Off-policy Eligibility Trace를 얻을 수 있습니다. 전자는 식 (12.19)나 (12.20)과 같은 일반적인 Action 기반 $\lambda$-Return에 대한 재귀 방법으로 시작해야 하지만, 후자(Expected Sarsa 형식)는 더 간단합니다. 식 (12.20)에 식 (7.14)를 결합하여 다음과 같이 Off-policy로 확장하면 되기 때문입니다.

\[\begin{align} G_t^{\lambda a} & \doteq R_{t+1} + \gamma_{t+1} \Big( (1 - \lambda_{t+1}) \bar{V}_{t} (S_{t+1}) + \lambda_{t+1} [ \rho_{t+1} G_{t+1}^{\lambda a} + \hat{V}_t (S_{t+1}) - \rho_{t+1} \hat{q} (S_{t+1}, A_{t+1}, \mathbf{w}_t) ] \Big) \\ \\ &= R_{t+1} + \gamma_{t+1} \Big( \bar{V}_t (S_{t+1}) + \lambda_{t+1} \rho_{t+1} \left[ G_{t+1}^{\lambda a} - \hat{q} (S_{t+1}, A_{t+1}, \mathbf{w}_t ) \right] \Big) \tag{12.26} \end{align}\]

식 (12.26)에서 $\bar{V}_t (S_{t+1})$은 식 (12.21)과 동일합니다. 그리고 또 다시  $\lambda$-Return은 TD Error의 합으로 표현할 수 있습니다.

\[G_t^{\lambda a} \approx \hat{q}(S_t, A_t, \mathbf{w}_t) + \sum_{k=t}^{\infty} \delta_k^a \prod_{i=t+1}^k \gamma_i \lambda_i \rho_i \tag{12.27}\]

식 (12.27)의 $\delta_t^a$는 다음과 같이 Action 기반 TD Error의 기대 형식으로 정의됩니다.

\[\delta_t^a = R_{t+1} + \gamma_{t+1} \bar{V}_t (S_{t+1}) - \hat{q} (S_t, A_t, \mathbf{w}_t) \tag{12.28}\]

식 (12.24)와 마찬가지로, Approximate Value Function $\hat{q}$가 변하지 않으면 식 (12.27)의 근사값은 정확해집니다.

State의 경우에 대한 과정과 유사한 과정을 사용하여 식 (12.27)에 기반한 Forward View Update를 유도하고, Summation Rule을 사용하여 Update의 합계를 변환한 후, 마지막으로 Action-Value에 대한 Eligibility Trace를 다음과 같이 유도할 수 있습니다.

\[\mathbf{z}_t \doteq \gamma_t \lambda_t \rho_t \mathbf{z}_{t-1} + \nabla \hat{q} (S_t, A_t, \mathbf{w}_t) \tag{12.29}\]

이 Eligibility Trace는 식 (12.28)과 같은 TD Error 및 식 (12.7)의 일반적인 Semi-gradient Update 규칙과 함께 On-policy, 또는 Off-policy에 적용할 수 있는 효율적인 Expected Sarsa($\lambda$) 알고리즘을 생성합니다. 이것은 아마도 현 시점에서 가장 좋은 알고리즘일 것입니다. (물론, 위에서 언급했듯이 아직까지는 안정성이 보장되지 않습니다.) On-policy의 경우 상수 $\lambda$와 $\gamma$, 그리고 식 (12.16)과 같은 State-Action TD Error를 사용한 알고리즘은 Section 12.7에서 제시된 Sarsa($\lambda$)와 동일합니다.

$\lambda = 1$에서 이러한 알고리즘은 Monte Carlo 알고리즘과 밀접한 관련이 있습니다. Episodic Task와 Off-line Update에 대해 정확하게 동일할 것으로 생각할 수도 있지만, 실제 관계는 그것보단 약합니다. 가장 간단한 조건은 Episode별로 Update가 없으며 기대치만 있는 경우입니다. 이 방법은 Trajectory가 이어짐에 따라 (철회할 수 없는) Update를 만들지만, True Monte Carlo Method는 Trajectory가 있는 경우 Target Policy 하에 0의 확률을 가진 Action이 있을 경우 Trajectory를 Update하지 않습니다. 특히 이 모든 방법들은 $\lambda = 1$일지라도 Target이 현재 Value에 대한 추정치에 의존하기 때문에 여전히 Bootstrap합니다. 이것이 실제로 좋은지 나쁜지는 또 다른 문제입니다.

관련 연구를 하나 소개하자면 (Sutton, Mahmood, Precup and van Hasselt, 2014)의 논문에서 정확한 동등성을 달성하는 방법이 제안되었습니다. 이 방법은 Update를 추적하지만, 나중에 취한 Action에 따라 철회할 수 있는 Provisional Weight라는 추가적인 Vector를 이용합니다. 이 방법의 State 및 State-Action 방법 버전을 각각 PTD($\lambda$)와 PQ($\lambda$)라고 합니다. 여기서 ‘P’는 Provisional의 약자입니다.

하지만 이러한 새로운 Off-policy 방법의 실질적인 결과는 아직 확립되지 않았습니다. 확실한 것은, Importance Sampling을 사용하는 모든 Off-policy 방법과 마찬가지로 높은 Variance 문제가 발생할 것입니다.

만약 $\lambda < 1$이면 모든 Off-policy 알고리즘은 Bootstrapping을 포함하고 Section 11.3에서 언급한 Deadly Traid가 적용됩니다. 이것은 Tabular, State Aggregation 및 기타 제한된 형태의 Function Approximation에 대해서만 안정성이 보장될 수 있다는 것을 의미합니다. Linear과 같은 보다 일반적인 형태의 Function Approximation의 경우, 매개변수 Vector는 11장의 예제에서와 같이 무한대로 발산할 수 있습니다. 11장에서 논의한 바와 같이 Off-policy 학습의 과제는 크게 두 부분으로 나눌 수 있습니다. Off-policy Eligibility Trace는 문제의 첫 번째 부분은 효과적으로 처리하여 Target의 Expected Value를 추정하지만, Update의 Distribution과 관련된 두 번째 문제는 전혀 처리하지 못합니다. Eligibility Trace를 포함한 Off-policy 학습에서 두 번째 문제를 해결하기 위한 알고리즘 전략은 Section 12.11에서 보일 예정입니다.

Watkins’s Q($\lambda$) to Tree-Backup($\lambda$)

Q-learning을 Eligibility Trace로 확장하기 위해 여러 방법이 제안되었습니다. 가장 처음 제안된 방법은 Watkins의 Q($\lambda$)로, Greedy Action이 수행되는 한 일반적인 방식으로 Eligibility Trace을 감소시킨 다음, 첫 번째 non-Greedy Action 후에 Trace를 0으로 줄입니다. Q($\lambda$)의 Backup Diagram은 다음과 같습니다.

6장에서 Q-learning과 Expected Sarsa를 통합하여 임의의 Target Policy로 일반화했으며, 이 장의 이전 Section에서 Expected Sarsa를 Off-policy Eligibility Trace로 일반화하였습니다. 그러나 7장에서는 Importance Sampling을 사용하지 않는 속성을 유지한 $n$-step Tree Backup과 $n$-step Expected Sarsa를 구분했습니다. 이제 우리는 Tree Backup의 Eligibility Trace 버전인 Tree Backup($\lambda$), 또는 TB($\lambda$)를 제시해야 합니다. 이는 Off-policy 데이터에 적용할 수 있음에도 불구하고 Importance Sampling이 없다는 장점이 있기 때문에 Q-learning의 진정한 확장이라고 볼 수 있습니다.

TB($\lambda$)의 개념은 간단합니다. Section 7.5에서와 같이 Tree Backup의 Update는 Bootstrapping Parameter $\lambda$에 따라 일반적인 방식으로 Weight가 부여됩니다. TB($\lambda$)의 Backup Diagram은 다음과 같습니다.

일반적인 Bootstrapping 및 Discounting Parameter에 대한 올바른 Index를 사용하여 구체적인 방정식을 얻으려면, 다음과 같이 식 (12.20) $\lambda$-Return의 재귀 형식으로 시작한 다음, 식 (7.16) Target의 Bootstrapping 경우로 확장하는 것이 가장 좋습니다.

\[\begin{align} G_t^{\lambda a} & \doteq R_{t+1} + \gamma_{t+1} \Big( (1 - \lambda_{t+1}) \bar{V}_t (S_{t+1}) + \lambda_{t+1} \big[ \sum_{a \ne A_{t+1}} \pi (a | S_{t+1}) \hat{q} (S_{t+1}, a, \mathbf{w}_t) + \pi (A_{t+1} | S_{t+1}) G_{t+1}^{\lambda a} \big] \Big) \\ \\ &= R_{t+1} + \gamma_{t+1} \Big( \bar{V}_t (S_{t+1}) + \lambda_{t+1} \pi (A_{t+1} | S_{t+1}) \big( G_{t+1}^{\lambda a} - \hat{v} (S_{t+1}, A_{t+1}, \mathbf{w}_t) \big) \Big) \end{align}\]

이전과 마찬가지로, $G_t^{\lambda a}$를 TD Error의 합으로 근사할 수도 있습니다. 이 때 TD Error는 식 (12.28)과 같은 형태를 사용합니다.

\[G_t^{\lambda a} \approx \hat{q} (S_t, A_t, \mathbf{w}_t) + \sum_{k=t}^{\infty} \delta_k^a \prod_{i=t+1}^k \gamma_i \lambda_i \pi (A_i | S_i)\]

이전 Section과 동일한 단계에 따라, 선택한 Action의 Target Policy 확률과 관련된 특별한 Eligibility Trace Update를 유도할 수 있습니다.

\[\mathbf{z}_t \doteq \gamma_t \lambda_t \pi (A_t | S_t) \mathbf{z}_{t+1} + \nabla \hat{q}(S_t, A_t, \mathbf{w}_t)\]

이것은 식 (12.7)과 같은 일반적인 매개변수 Update 규칙과 함께 TB($\lambda$) 알고리즘을 정의합니다. 모든 Semi-gradient 알고리즘과 마찬가지로 TB($\lambda$)는 Off-policy 데이터와 강력한 Function Approximation 방법과 함께 사용했을 때 안정성이 보장되지 않습니다. 안정성을 보장받기 위해서는 TB($\lambda$)를 다음 Section에 나오는 방법 중 하나와 결합해야 합니다.

Stable Off-policy Methods with Traces

Eligibility Trace를 사용한 Off-policy 학습에서 안정성을 보장하기 위한 여러 방법이 제안되었습니다. 여기에서는 일반적인 Bootstrapping 및 Discount Function을 포함한 네 가지 방법을 제시합니다. 이 방법들은 모두 Section 11.7과 11.8에 제시한 Gradient-TD 또는 Emphatic-TD의 아이디어에 기반하고 있습니다. 모든 알고리즘은 Linear Function Approximation를 사용한다고 가정하지만, non-Linear Function Approximation에 대한 확장도 여러 논문에서 찾을 수 있습니다.

첫 번째 방법으로 GTD($\lambda$)는 TDC와 유사한 Eligibility Trace 알고리즘으로, Section 11.7에서 제시한 두 가지 State-Value Gradient TD 예측 알고리즘보다 우수합니다. 이 알고리즘의 목표는 Behavior Policy $b$를 따르는 데이터를 위해 $\hat{v} (s, \mathbf{w}) \doteq \mathbf{w}_t^{\sf T} \mathbf{x} (s) \approx v_{\pi}(s)$와 같은 식에서 매개변수 $\mathbf{w}_t$를 학습하는 것입니다. 이 방법의 Update 식은 다음과 같습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t^s \mathbf{z}_t - \alpha \gamma_{t+1} (1 - \lambda_{t+1}) (\mathbf{z}_t^{\sf T} \mathbf{v}_t) \mathbf{x}_{t+1}\]

위 식에서 $\delta_t^s$는 식 (12.23), $\mathbf{z}$는 식 (12.25), $\rho_t$는 식 (11.1)과 같습니다. 그리고 $\mathbf{v}_t$는 다음과 같이 정의됩니다.

\[\mathbf{v}_{t+1} \doteq \mathbf{v}_t + \beta \delta_t^s \mathbf{z}_t - \beta (\mathbf{v}_t^{\sf T} \mathbf{x}_t) \mathbf{x}_t \tag{12.30}\]

Section 11.7에서와 같이 $\mathbf{v} \in \mathbb{R}^d$는 $\mathbf{w}$와 같은 차원의 Vector이고, $\mathbf{v} = \mathbf{0}$으로 초기화됩니다. 그리고 $\beta > 0$은 두 번째 Step-size Parameter입니다.

두 번째 방법인 GQ($\lambda$)는 Eligibility Trace가 포함된 Action-Value에 대한 Gradient-TD 알고리즘입니다. 이 알고리즘의 목표는 Off-policy 데이터에서 $\hat{q} (s, a, \mathbf{w}_t) \doteq \mathbf{w}_t^{\sf T} \mathbf{x}(s, a) \approx q_{\pi} (s, a)$와 같은 식의 매개변수 $\mathbf{w}_t$를 학습하는 것입니다. 만약 Target Policy가 $\epsilon$-greedy인 경우, 또는 $\hat{q}$에 대한 Greedy Policy로 Bias되는 경우 GQ($\lambda$)를 Control 알고리즘으로 사용할 수 있습니다. 이 방법의 Update는 다음과 같습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w} + \alpha \delta_t^a \mathbf{z}_t - \alpha \gamma_{t+1} (1 - \lambda_{t+1}) (\mathbf{z}_t^{\sf T} \mathbf{v}_t) \bar{\mathbf{x}}_{t+1}\]

위 식에서 $\bar{\mathbf{x}}_t$는 Target Policy를 따르는 $S_t$에 대한 평균 Feature Vector로 정의됩니다.

\[\bar{\mathbf{x}}_t \doteq \sum_a \pi (a | S_t) \mathbf{x} (S_t, a)\]

또한 $\delta_t^a$는 다음과 같은 TD Error로 정의됩니다.

\[\delta_t^a \doteq R_{t+1} + \gamma_{t+1} \mathbf{w}_t^{\sf T} \bar{\mathbf{x}}_{t+1} - \mathbf{w}_t^{\sf T} \mathbf{x}_t\]

$\mathbf{z}_t$는 식 (12.29)와 동일하게 정의되고, $\mathbf{v}_t$의 Update를 포함한 나머지는 GTD($\lambda$)와 동일합니다.

세 번째로 HTD($\lambda$)는 GTD($\lambda$)와 TD($\lambda$)를 결합한 State-Value 알고리즘입니다. 이 알고리즘의 가장 큰 장점은 TD($\lambda$)를 Off-policy 학습으로 엄격하게 일반화한다는 것입니다. 엄격하게 라는 의미는 Behavior Policy가 Target Policy와 같게 되면 HTD($\lambda$)가 TD($\lambda$)와 동일하게 된다는 뜻입니다. (GTD($\lambda$)는 그렇게 되지 않습니다.) 보통 TD($\lambda$)가 GTD($\lambda$)보다 빠르게 수렴하기 때문에 이 장점은 매력적입니다. 또한 TD($\lambda$)는 단일 Step-size Parameter만 필요하다는 장점도 있습니다. HTD($\lambda$)는 다음과 같이 정의됩니다.

\[\begin{align} \mathbf{w}_{t+1} & \doteq \mathbf{w}_t + \alpha \delta_t^s \mathbf{z}_t + \alpha \big( (\mathbf{z}_t - \mathbf{z}_t^b)^{\sf T} \mathbf{v}_t \big) (\mathbf{x}_t - \gamma_{t+1} \mathbf{x}_{t+1}) \\ \\ \mathbf{v}_{t+1} & \doteq \mathbf{v}_t \beta \delta_t^s \mathbf{z}_t - \beta \Big( \mathbf{z}_t^{b^{\sf T}} \mathbf{v}_t \Big) (\mathbf{x}_t - \gamma_{t+1} \mathbf{x}_{t+1}) \quad \text{with} \quad \mathbf{v}_0 \doteq \mathbf{0} \\ \\ \mathbf{z}_t & \doteq \rho_t \big( \gamma_t \lambda_t \mathbf{z}_{t-1} + \mathbf{x}_t \big) \quad \text{with} \quad \mathbf{z}_{-1} \doteq \mathbf{0} \\ \\ \mathbf{z}_t^b & \doteq \gamma_t \lambda_t \mathbf{z}_{t-1}^b + \mathbf{x}_t \quad \text{with} \quad \mathbf{z}_{-1}^b \doteq \mathbf{0} \end{align}\]

위 식에서 $\beta > 0$은 두 번째 Step-size Parameter입니다. 또한 두 번째 Weight 집합인 $\mathbf{v}_t$ 외에도 HTD($\lambda$)는 두 번째 Eligibility Trace 집합인 $\mathbf{z}_t^b$가 있습니다. 이것들은 Behavior Policy에 대한 누적된 Eligibility Trace이며, 모든 $\rho_t$가 1이면 $\mathbf{w}_t$ Update의 마지막 항이 0이 되면서 $\mathbf{z}_t$와 같아집니다.

마지막으로 Emphatic TD($\lambda$)는 1-step Emphatic-TD 알고리즘을 Eligibility Trace로 확장한 것입니다. (Section 9.11과 11.8 참고) 결과적으로 이 알고리즘은 강력한 Off-policy 수렴을 보장하면서 어느 정도 Bootstrapping도 가능하게 하지만, 높은 Variance를 가지고 수렴 속도가 느리다는 단점이 있습니다. Emphatic TD($\lambda$)는 다음과 같이 정의됩니다.

\[\begin{align} \mathbf{w}_{t+1} & \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t \\ \\ \delta_t & \doteq R_{t+1} + \gamma_{t+1} \mathbf{w}_t^{\sf T} \mathbf{x}_{t+1} - \mathbf{w}_t^{\sf T} \mathbf{x}_t \\ \\ \mathbf{z}_t & \doteq \rho_t \left( \gamma_t \lambda_t \mathbf{z}_{t-1} + M_t \mathbf{x}_t \right) \quad \text{with} \quad \mathbf{z}_{-1} \doteq \mathbf{0} \\ \\ M_t & \doteq \lambda_t I_t + \left( 1 - \lambda_t \right) F_t \\ \\ F_t & \doteq \rho_{t-1} \gamma_t F_{t-1} + I_t \quad \text{with} \quad F_0 \doteq i (S_0) \end{align}\]

위 식에서 $M_t \ge 0$은 Emphasis의 일반적인 형태이고, $F_t \ge 0$은 Followon Trace라고 하며, $I_t \ge 0$은 Section 11.8에서 설명한 Interest입니다. 이 알고리즘의 중요한 점은 $\delta_t$와 같이 $M_t$ 또한 공간 복잡도를 높이지 않는다는 것입니다. 이 식의 정의를 Eligibility Trace 식에 대입하여 처리가 가능합니다. Emphatic TD($\lambda$)의 True On-line 버전에 대한 Pseudocode 및 프로그램은 (Sutton, 2015b) 논문에서 확인이 가능합니다.

On-policy의 경우 (즉, 모든 $t$에 대해 $\rho_t = 1$) Emphatic TD($\lambda$)는 기존 TD($\lambda$)와 유사하지만 차이점도 많습니다. 예를 들어, Emphatic TD($\lambda$)는 모든 State에 종속적인 $\lambda$ 함수에 대해 수렴이 보장되지만, TD($\lambda$)는 그렇지 않습니다. TD($\lambda$)는 모든 상수 $\lambda$에 대해서만 수렴이 보장됩니다. 이에 대한 반례는 (Ghiassian, Rafiee, and Sutton, 2016) 논문을 참고해주시기 바랍니다.

Implementation Issues

처음에는 Eligibility Trace를 사용하는 Tabular 방법이 1-step 방법보다 복잡해 보일 수도 있습니다. 단순한 구현은 모든 State(또는 State-Action 쌍)가 모든 시간 단계에서 Estimated Value와 Eligibility Trace를 모두 Update해야 합니다. 이것은 단일 명령, 다중 데이터, 병렬 컴퓨터 또는 Artificial Neural Network에서 구현하는 경우 문제가 되지 않지만, 기존의 직렬 컴퓨터에서 구현하는 경우에는 문제가 될 수 있습니다. 다행히도 일반적인 $\lambda$와 $\gamma$에 대해 거의 모든 State에서의 Eligibility Trace는 항상 0에 가깝습니다. 최근에 방문한 State에서만 0보다 훨신 큰 Trace가 있을 것이기 때문에 이러한 몇 개의 State만 Update하여 구현함으로써 간단하게 알고리즘을 근사적으로 구현할 수 있습니다.

실제로 이러한 방법을 사용하면 기존 컴퓨터로도 0보다 훨씬 큰 일부 Trace만 Update함으로써 구현할 수 있습니다. 이러한 꼼수를 사용하면 Tabular 방법에서 Trace를 사용하는 계산 비용이 일반적인 1-step 방법의 몇 배에 불과합니다. 물론 정확한 배수는 $\lambda$ 및 $\gamma$의 값과 다른 계산 비용에 따라 달라집니다. Tabular 방법의 경우는 어떤 의미에서 Eligibility Trace의 최악의 계산 복잡도를 가지고 있습니다. Function Approximation을 사용할 때는 Function Approximation 방법 자체의 계산 복잡도가 높기 때문에 Eligibility Trace를 사용하지 않는 것과 크게 차이가 나지 않기 때문입니다. 예를 들어, Artificial Neural Network 및 Backpropagation Algorithm을 사용하는 경우 Eligibility Trace를 추가해도 각 단계별로 필요한 메모리나 계산량이 두 배 정도만 늘어납니다. Section 12.3의 Truncated $\lambda$-Return 방법은 항상 추가적인 메모리 용량이 필요하지만, 기존 컴퓨터에서 계산적으로 효율적인 구현이 가능하기도 합니다.

Conclusions

TD Error를 사용하는 Eligibility Trace는 Monte Carlo와 TD 방법의 중간 지점을 선택할 수 있는 효율적이고 점진적인 방법을 제공합니다. 7장의 $n$-step TD 방법도 이것을 가능하게 했지만 Eligibility Trace 방법은 더 일반적이고 더 빨리 학습할 수도 있으며 Trade-off를 통해 다른 계산 복잡성을 가질 수도 있습니다. 이번 장에서는 On-policy와 Off-policy 학습에서 Variable Bootstrapping 및 Discounting을 위해 Eligibility Trace에 대한 새로운 이론을 제시했습니다. 이 이론의 하나로써 기존 TD 방법의 계산 복잡도를 유지한 채 이상적인 방법의 Action을 정확하게 재현하는 True On-line 방법이 있습니다. 또 다른 것으로는 직관적인 Forward View 방법에서 보다 계산적으로 효율적인 Backward View로 전환할 수 있는 가능성입니다. 이제 고전적이고 계산량이 많은 Monte Carlo 알고리즘으로 시작하여 True On-line TD 방법에 사용한 것과 동일한 Eligibility Trace를 사용하여 계산량이 적은 Incremental non-TD를 구현함으로써 이 일반적인 아이디어를 설명했습니다.

5장에서 언급했듯이 Monte Carlo Method은 Bootstrap하지 않기 때문에 non-Markov Process에서 이점이 있을 수 있습니다. Eligibility Trace는 TD 방법을 Monte Carlo Method와 유사하게 만들기 때문에 이런 경우에도 이점을 가질 수 있습니다. 예를 들어, TD 방법의 장점으로 인해 이것을 사용하고 싶지만, 일부 작업이 non-Markov인 경우 Eligibility Trace를 도입함으로써 이 문제를 해결할 수 있습니다. Eligibility Trace는 장기간의 지연된 Reward와 non-Markov Process 모두에 대한 해결 방법을 가지고 있습니다.

$\lambda$의 값을 조절하여 Monte Carlo에서 1-step TD 방법에 이르기까지 Eligibility Trace를 어디에나 사용할 수 있습니다. 그렇다면 어느 단계에서 사용하는 것이 가장 좋을까요? 안타깝게도 이 질문에 대한 명확한 이론적인 답이 없습니다. 대신 경험적인 답으로써, Episode당 단계가 많거나 Discounting이 반감기 내에 단계가 많은 작업에서 Eligibility Trace를 사용하는 것이 더 좋다고 판단됩니다. 아래의 그래프는 $\lambda$에 따른 강화학습의 성능을 나타내고 있는데, 이것을 통해 대략적인 답을 낼 수 있습니다.

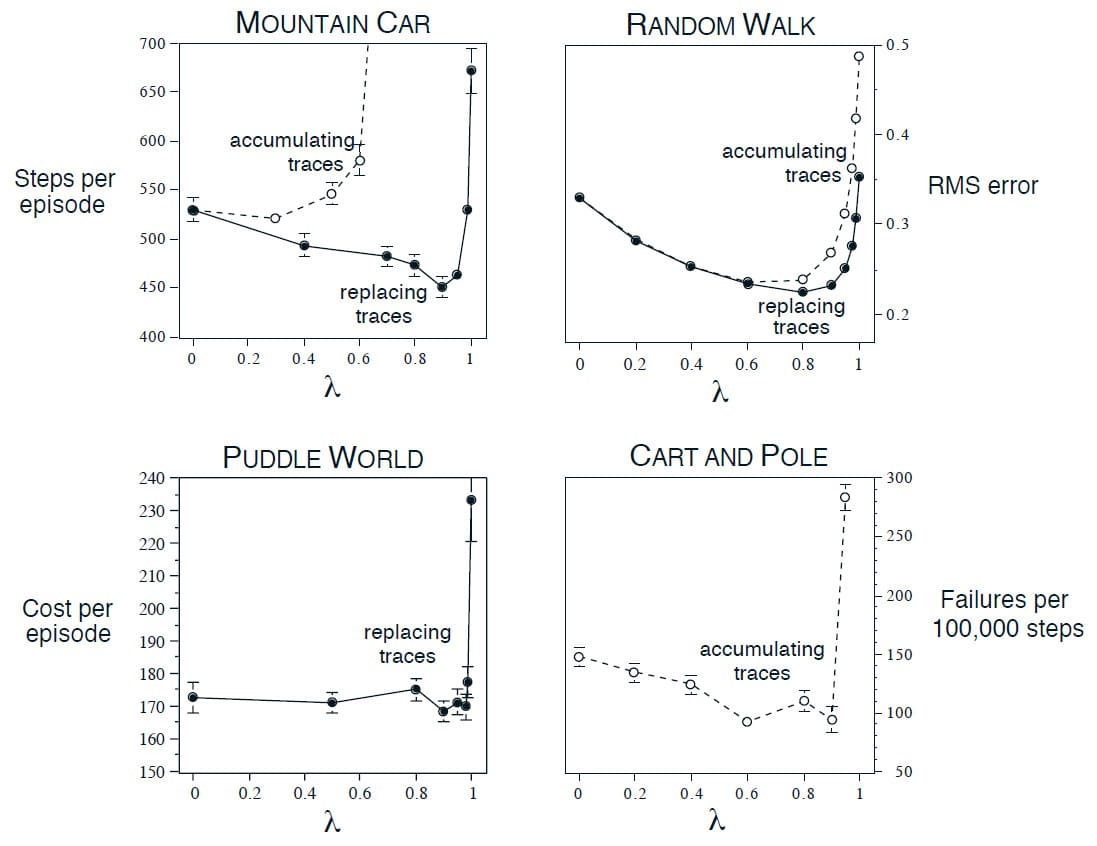
반면에 순수한 Monte Carlo Method에 가까워지면 성능이 급격히 저하됩니다. 그렇기 때문에 적당히 중간 정도의 Step이 최선의 선택이라고 볼 수 있습니다. 미래에는 $\lambda$를 사용하여 TD와 Monte Carlo Method 간 Trade-off를 더 미세하게 조절하는 것이 가능할 수도 있겠지만, 현재로서는 이것을 어떻게 안정적이고 유용하게 사용할 수 있을지 명확한 결론을 내릴 수가 없습니다.

Eligibility Trace를 사용하게 되면 1-step 방법보다 더 많은 계산이 필요하지만, 그 대가로 Reward가 여러 단계로 지연되는 경우 훨씬 더 빠른 학습 속도를 제공합니다. 따라서 On-line과 같이 데이터가 부족하고 반복적으로 처리할 수 없는 경우에는 Eligibility Trace를 사용하는 것이 좋습니다. 반면에, 시뮬레이션을 통해 데이터를 쉽게 생성할 수 있는 Off-line의 경우에는 Eligibility Trace를 사용하는데 큰 이점이 없는 경우가 많습니다. 이 때의 목표는 제한된 데이터에서 더 많은 것을 얻는 것이 아니라 가능한 한 빠르게 많은 데이터를 처리하는 것인데, Eligibility Trace로 인한 데이터의 속도 향상은 그만한 계산 비용를 소모할 가치가 없기 때문에 1-step 방법이 선호됩니다.

이번 장은 내용이 길고 어려워서 그런지 깔끔하게 포스트를 작성하지 못한 것 같네요. 포스트를 먼저 게시한 다음 나중에 다시 읽어보며 조금씩 매끄럽게 수정하겠습니다.

다음 장은 강화학습의 마지막 장인 Policy Gradient Methods입니다. 읽어주셔서 감사합니다!