Multi-armed Bandits

Part I: Tabular Solution Methods

이 책은 크게 두 부분으로 나뉘어져 있습니다. 첫 번째는 강화학습에서 State와 Action을 Table에 정리하는 방법입니다. Table을 사용하는 Tabular Method는 대부분의 문제에서 Optimal Policy를 정확하게 찾을 수 있다는 것을 보장하지만 State의 집합과 Action의 집합이 Table을 사용할 수 있을만큼 충분히 작아야 한다는 단점이 있습니다. 두 번째는 Table을 사용하지 않고 State와 Action에 대한 함수를 추정하는 방법인 Approximation Method가 있습니다. 함수를 추정하는 방법은 State와 Action의 집합 크기가 크더라도 (심지어 무한대라고 하더라도) Policy를 구할 수 있지만 Optimal Policy를 보장하기 힘들다는 단점이 있습니다.

Tabular Method의 첫 번째는 단일 State만 갖고 있는 Bandit 문제를 해결하는 것으로 시작합니다. (2장) 다음으로는 Finite Markov Decision Process (Finite MDP)와 Bellman Equation, Value Function에 대한 주요 아이디어를 설명합니다. (3장)

그 다음으로 3개 장에 걸쳐 Finite Markov Decision Process를 해결할 수 있는 방법들을 하나씩 소개합니다. 4장에서 Dynamic Programming, 5장에서 Monte Carlo Method, 그리고 6장에서 Temporal-Difference Learning에 대해 소개합니다. 이 방법들은 각각 장점과 단점이 있기 때문에 어느 하나가 우월하다고 표현하기 어렵습니다. Dynamic Programming은 수학적으로 잘 설계되었으나 Environment에 대해 완전하고 정확한 Model이 필요하다는 단점이 있습니다. Monte Carlo Method은 Model이 필요하지 않고 개념적으로 간단하지만 Step-by-step으로 계산하기 적합하지 않다는 단점이 있습니다. Temporal-Difference Learning도 Model이 필요하지 않고 Step-by-step으로 계산하기 적합하지만, 그만큼 복잡하다는 단점이 있습니다. 또한 이 3가지 방법들은 각각 효율성과 수렴 속도도 차이가 납니다.

나머지 2개 장에서는 이 세 가지 방법을 결합하여 각각의 최상의 기능을 얻는 방법을 설명합니다. 7장에서는 Monte Carlo Method의 장점인 Multi-step bootstrapping method를 Temporal-Difference Learning과 결합할 수 있는 방법을 설명합니다. 마지막으로 8장에서는 Tabular Method 강화학습 문제에 대한 완전하고 통합된 솔루션을 위해 Temporal-Difference Learning이 Model Learning 및 Planning과 결합할 수 있는 방법을 소개하도록 하겠습니다.

A $k$-armed Bandit Problem

$k$-armed Bandit는 $k$ 개의 레버가 달린 슬롯머신을 말합니다. 도박은 결국 돈을 잃을 가능성이 높기 때문에 슬롯머신을 Bandit라고 부르는 것 같습니다. 원래라면 슬롯머신 따위는 거들떠보지도 않겠지만, 여기서는 꼭 이 슬롯머신을 플레이해야하는 상황이라고 가정해보겠습니다.

우리는 한 번의 게임에서 슬롯머신의 레버 중 하나를 선택하여 당길 수 있습니다. 그런데 이 슬롯머신은 특이하게 각 레버마다 Reward가 다르게 설정되어 있습니다. 물론 어떤 레버가 가장 높은 보수를 받는지는 모르는 상황입니다. 또한 각 레버의 Reward는 고정된 값이 아니라 확률 분포로 이루어져 있습니다. 따라서 레버를 당겼을 때 낮은 Reward가 나왔다고 해도 레버의 Reward가 낮게 설정되어 있는 것인지, 아니면 운이 나빠서 낮은 Reward가 나온 것인지 알 수 없습니다. 물론 같은 레버를 여러번 플레이한다면 대략적인 확률 분포를 예측할 수는 있습니다.

이런 상황에서 특정 시간이 주어졌을 때(예를 들면 총 1000번의 게임, 또는 T 시간) Reward를 최대화하는 Policy를 찾는 것이 $k$-armed Bandit Problem입니다.

먼저 $k$-armed Bandit Problem에서 $k$개의 Action에 대한 평균적인 Reward를 수식화해보겠습니다. 즉, 각 Action의 Value를 수학적으로 표현하는 것입니다. $t$라는 시간에서 선택한 Action을 $A_t$라고 하고, 그 때 받는 Reward를 $R_t$로 정의합니다. 임의의 Action $a$에 대한 Value를 $q_{*}(a)$라고 하면, $q_{*}(a)$는 다음과 같이 나타낼 수 있습니다.

\[q_*(a) \doteq \mathbb{E} \left[ R_t \mid A_t = a \right]\]

만약 각 Action에 대한 Value를 알고 있다면 항상 가장 높은 Value를 가진 Action을 선택함으로써  $k$-armed Bandit Problem을 해결할 수 있습니다. 하지만 여기서는 각 Action의 정확한 Value를 알지 못하고 대략적인 추정치만 알고 있다고 가정해봅시다. $t$라는 시간에서 Action $a$의 Value를 추정한 것이 $Q_t (a)$라고 하면, $Q_t (a)$가 $q_*(a)$에 가까울수록 정확한 정답을 계산할 수 있습니다.

우리는 아무런 정보가 없는 상황에서 슬롯머신의 레버를 어느 정도 당겨보고 각 레버에 대한 대략적인 추정치를 알게 되었습니다. 이제 또 어떤 레버를 당길지 선택을 해야하는데, 이 때 두 가지 선택이 있습니다. 첫째로 지금까지 당겼던 레버 중 가장 높은 Reward를 제공했던 레버를 당기는 것입니다. 이러한 Action을 Greedy Action이라고 합니다. 강화학습에서 이것은 지금까지의 경험을 활용하는 것이기 때문에 Exploitation이라고 부릅니다. 다른 또 하나의 선택은 정보가 부족한 다른 레버를 당겨보는 것입니다. 왜냐하면 내가 당겨보지 않았거나, 적게 당겨보았던 레버가 알고보니 내가 알고있는 레버보다 더 높은 Reward를 제공할 수도 있기 때문입니다. 이렇게 다른 Action을 탐색하는 행위를 강화학습에서는 Exploration이라고 부릅니다. Exploration을 하는 동안의 Reward는 Exploitation을 할 때보다 낮겠지만, 더 좋은 Action을 찾고 난 다음에는 더 높은 Reward를 얻을 수 있기 때문에 장기적으로 봤을 때 Exploration이 더 좋을 수도 있습니다. 여기서 주어진 시간 동안 어느 만큼의 Exploration을 하고 어느 만큼의 Exploitation을 할 지도 문제가 됩니다. 또한 어떤 상황에 Exploration을 해야하고 어떤 상황에 Exploitation을 해야하는 지는 각 Action의 추정치가 얼마나 정확한지, 남은 시간 단계가 얼마나 되는지에 따라 달라집니다. 또 생각해 볼 수 있는 문제는 Exploration을 효율적으로 하기 위해 주어진 Action 중 어떤 Action을 선택해야할지도 있겠지만, 이 책에서는 그런 것보다 Exploration과 Exploitation을 얼마나 균형있게 선택하는지를 더 중점적으로 다룰 예정입니다.

Action-value Methods

이제 각 Action에 대한 가치를 추정하는 방법과 어떤 Action을 선택할지 결정을 내리기 위해 추정한 값을 사용하는 방법에 대해 알아보도록 하겠습니다. 각 Action의 Value는 그 Action을 선택했을 때의 평균적인 Reward로 정의할 수 있습니다. 즉, $Q_t (a)$는 다음과 같이 표현할 수 있습니다.

\[\begin{align} Q_t (a) & \doteq \frac{\text{sum of rewards when } a \text{ taken prior to } t }{\text{number of times } a \text{ taken prior to }t} \\ \\ &= \frac{\sum_{i=1}^{t-1} R_i \cdot 1_{A_t = a}}{\sum_{i=1}^{t-1} 1_{A_t = a}} \tag{2.1} \end{align}\]

여기서 $1_{A_t = a}$는 $A_t = a$가 true면 1이고 그렇지 않으면 0을 나타내는 확률 변수입니다. 초기에는 분모가 0이기 때문에 $Q_t (a)$에 적절한 초기값(이를테면 0)을 설정합니다. 분모가 무한대에 가까워질수록 $Q_t (a)$는 $q_{*}(a)$에 수렴합니다. 이런 방법으로 Action의 Value를 추정하는 것을 Sample-average method라고 합니다. Action에 대한 Value를 추정하는 방법은 이외에도 있지만, 여기서 그것까지 다루지는 않고 어떻게 추정값을 통해 Action을 선택하는지를 알아보도록 하겠습니다.

가장 간단하게 Action을 선택하는 방법은 추정 Value가 가장 높은 Action을 선택하는 것입니다. 즉, Greedy Action을 선택하는 방법입니다. 만약 가장 높은 Value를 가지는 Action이 2개 이상 있다면 그 중 무작위로 선택한다고 가정합니다. 이것을 수식으로 표현하면 다음과 같습니다.

\[A_t \doteq \underset{a}{\operatorname{argmax}} \ Q_t (a) \tag{2.2}\]

$\underset{a}{\operatorname{argmax}} \ Q_t (a)$는 $Q_t(a)$을 최대값으로 만드는 $a$라는 뜻입니다. 식 (2.2)과 같은 Greedy 방법은 현재 알고 있는 정보를 기반으로 즉각적인 Reward를 최대화하는 전략입니다. 다시 말해, 더 나은 Action이 있을지도 모르지만 Reward가 낮은 Action을 Exploration하는데 전혀 시간을 들이지 않습니다.

이에 대한 대안으로 $\epsilon$-greedy 방법이 있습니다. 이것은 대부분 Greedy하게 Action을 선택하지만 작은 확률($\epsilon$)로 무작위 Action을 선택하는 방법입니다. 이 방법은 시간이 무한대에 가까워지면 모든 Action 또한 무한대로 샘플링되므로 모든 $Q_t (a)$가 $q_{*}(a)$에 수렴하는 것을 보장한다는 장점이 있습니다. $\epsilon$-greedy 방법은 강화학습에서 Action을 선택하는 전략으로 매우 많이 사용하기 때문에 나중에 더 자세히 설명하도록 하겠습니다.

The 10-armed Testbed

greedy 방법과 및 $\epsilon$-greedy 방법을 비교하기 위해 구체적인 예제를 하나 살펴보도록 하겠습니다. 예제는 $k$를 10으로 설정하고 무작위로 2000개의 $k$-armed bandit 문제를 생성하였습니다. 각 Action $a$에 대해 $q_{*}(a)$는 평균이 0이고 분산이 1인 정규분포에 따라 만들어졌습니다. 또한 Agent가 Action을 선택하였을 때 받는 Reward 또한 평균이 $q_{*}(A_t)$이고 분산이 1인 정규분포를 따르도록 설정하였습니다. 이러한 분포를 그림으로 표현하면 아래와 같습니다.

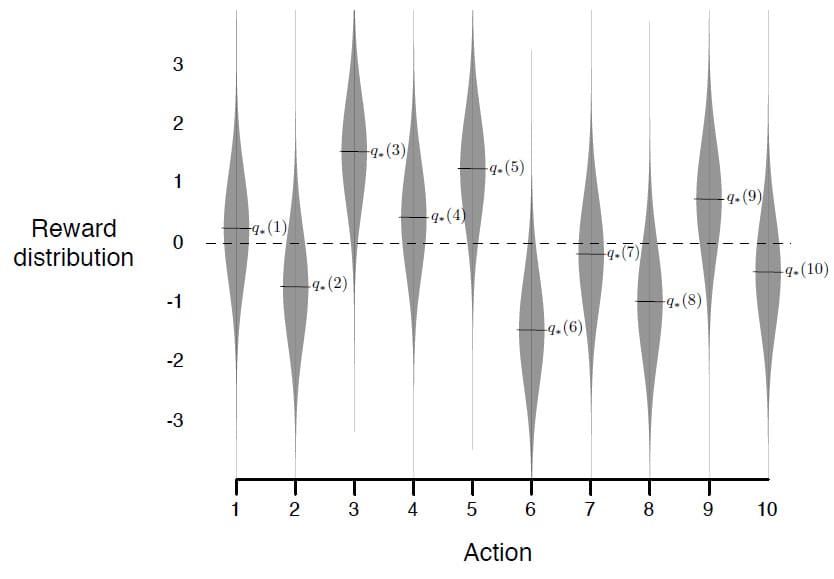
이렇게 테스트한 작업 모음을 10-armed testbed라고 부릅니다. 어떤 학습 방법이든 한 번에 1000개 이상의 시간 단계 정도면 학습 성능과 동작이 얼마나 향상되었는지 대략적으로 측정할 수 있습니다. 이것을 하나의 Run이라고 합니다. 본 예제에는 총 2000개의 독립적인 Run에 대해 학습 알고리즘의 평균적인 측정값을 구했습니다.

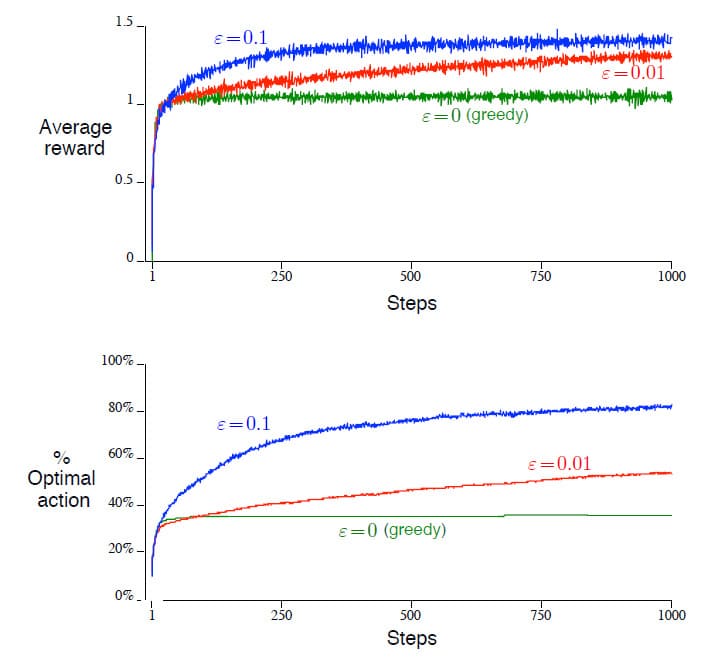
위의 그래프는 $\epsilon$의 값에 따른 성능을 비교한 결과입니다. 성능 비교는 크게 2가지 관점에서 측정하였는데, 위의 그래프는 평균 Reward를 나타내고 아래의 그래프는 Optimal Action을 선택하는 비율을 나타냅니다. $\epsilon$은 각각 0.1과 0.01, 그리고 0(=Greedy)의 3가지로 나누었습니다. Greedy 방법은 초기에는 다른 두 비교군에 비해 좋은 성능을 보이지만, Exploration을 전혀 하지 않기 때문에 적당히 좋은 Action에만 고집하게 됩니다. 시간이 흐를수록 다른 비교군에 비해 성능이 월등히 떨어짐을 알 수 있습니다. $\epsilon$이 0.1일 때와 0.01일 때를 비교해보면 0.1인 경우가 비교적 빠른 시간 안에 높은 결과를 보임을 알 수 있습니다. 하지만 이것은 시간 단계가 1000에서 멈추었기 때문이고, 더 많은 시간이 주어진다면 개선 시간은 느릴지언정 결국 0.01일 때 0.1보다 높은 성능을 보일 가능성이 높습니다. 이 두 가지 방법의 장점을 모두 활용하기 위해 초기에는 $\epsilon$의 값을 높게 잡다가 시간이 지남에 따라 줄이는 것도 하나의 방법이 될 수 있습니다.

$\epsilon$-greedy 방법과 Greedy 방법 중 어느 것이 더 우수한지는 환경이 어떻게 주어졌는지에 따라 다릅니다. 예를 들어 Reward의 분산이 1이 아니라 10이라면 그만큼 Exploration이 더 많이 필요하게 되며, 이 때는 $\epsilon$-greedy 방법이 확실히 우수한 방법이라고 말할 수 있습니다. 하지만 반대로 Reward의 분산이 0이라면 오히려 Exploration을 하는 만큼 손해가 커지게 되므로, Greedy 방법이 더 우수한 결과가 나올 수 있습니다. 이렇게 되면 Deterministic 문제에서는 Greedy 방법만 사용해야할 것 같지만, 꼭 그렇지도 않습니다. 예를 들어 Deterministic 문제에서도 각 Action이 가지는 Reward가 시간이 지남에 따라 변경된다면 Exploration이 반드시 필요하게 되므로 $\epsilon$-greedy 방법을 사용해야하기 때문입니다. 이런 케이스는 생각보다 흔하게 접할 수 있으므로 앞으로 배울 강화학습에서 많이 다룰 예정입니다. 심지어 Deterministic이면서 Stationary인 경우라도 의사 결정 정책 자체가 변경되는 경우도 있으므로 Exploration을 아예 배제할 수는 없습니다. 즉, 강화학습에서는 Exploration과 Exploitation 사이의 균형이 필요합니다.

Incremental Implementation

지금까지 다루었던 방법들은 모두 평균적으로 어느 정도의 Reward를 얻었는지에 따라 Action에 대한 Value를 추정했습니다. 이번에는 평균 Reward를 어떻게 효율적으로 계산할 것인지에 대해 알아보도록 하겠습니다. 먼저 표기법을 단순히하기 위해 몇 가지 기호를 정의하겠습니다. $R_i$는 이 Action을 $i$번째 선택한 후 받은 Reward를 나타냅니다. 그리고 $Q_n$은 이 Action을 $n-1$번 선택한 후에 Action에 대한 Value를 추정한 값을 의미합니다. 이것을 수식으로 표현하면 다음과 같습니다.

\[Q_n \doteq \frac{R_1 + R_2 + \ldots + R_{n-1}}{n-1}\]

이것을 그대로 구현하려면 $Q_n$이 필요할 때마다 저장된 모든 Reward를 체크하여 계산을 수행해야 합니다. 문제는 이렇게 하면 시간이 지날 때마다 Reward를 저장해야하는 메모리가 계속 증가할 수밖에 없습니다. 그렇기 때문에 아래처럼 Recurrence Relation 형태로 만들면 Reward를 저장할 필요 없이 간단하게 계산할 수 있습니다.

\[\begin{align} Q_{n+1} &= \frac{1}{n} \sum_{i=1}^n R_i \\ &= \frac{1}{n} \left( R_n + \sum_{i=1}^{n-1} R_i \right) \\ &= \frac{1}{n} \left( R_n + (n-1) \frac{1}{n-1} \sum_{i=1}^{n-1} R_i \right) \\ &= \frac{1}{n} \bigg( R_n + (n-1) Q_n \bigg) \\ &= \frac{1}{n} \bigg( R_n + n Q_n - Q_n \bigg) \\ &= Q_n + \frac{1}{n} \bigg[ R_n - Q_n \bigg] \tag{2.3} \end{align}\]

이 Recurrence Relation은 $n=1$부터 가능합니다. Recurrence Relation을 사용함으로써 메모리에 $Q_n$, $n$만 저장하면 되고 계산도 간단한다는 장점이 있습니다.

이전에 배운 $\epsilon$-greedy 방법과 Recurrence Relation을 사용하여 완전한 Bandit 알고리즘을 Pseudocode (의사코드)로 작성하면 다음과 같습니다. 함수 $bandit(a)$는 Action $a$를 선택하고 Reward를 반환한다고 가정합니다.

Tracking a Nonstationary Problem

평균을 사용하여 Action의 Value를 측정하는 방법은 Reward가 고정된 Stationary Problem에 적합합니다. 하지만 같은 Action을 하더라도 시간에 따라 Reward가 변하는 Nonstationary Problem에서는 과거의 Reward보다 최근의 Reward에 더 많은 가중치를 두는 것이 합리적입니다. 이것을 위해 가장 많이 쓰이는 방법은 Step-size parameter를 사용하는 것입니다. 예를 들어, 직전에 다룬 Recurrence Relation을 다음과 같이 수정해보겠습니다.

\[Q_{n+1} \doteq Q_n + \alpha \bigg[ R_n - Q_n \bigg] \tag{2.5}\]

이전 식에서 $\frac{1}{n}$를 상수 $\alpha \in (0,1]$로 수정한 것입니다. 하지만 수정된 Recurrence Relation을 다시 풀어써보면 어떤 차이가 있는지 알 수 있습니다.

\[\begin{align} Q_{n+1} &= Q_n + \alpha \bigg[ R_n - Q_n \bigg] \\ \\ &= \alpha R_n + (1 - \alpha) Q_n \\ \\ &= \alpha R_n + (1 - \alpha) \left[ \alpha R_{n-1} + (1 - \alpha) Q_{n-1} \right] \\ \\ &= \alpha R_n + (1 - \alpha) \alpha R_{n-1} + (1 - \alpha)^2 Q_{n-1} \\ \\ &= \alpha R_n + (1 - \alpha) \alpha R_{n-1} + (1 - \alpha)^2 \alpha R_{n-2} + \\ \\ & \qquad \qquad \cdots + (1 - \alpha)^{n-1} \alpha R_1 + (1 - \alpha)^n Q_1 \\ \\ &= (1 - \alpha)^n Q_1 + \sum_{i=1}^n \alpha (1 - \alpha)^{n-i} R_i \tag{2.6} \end{align}\]

식 (2.6)의 마지막 부분을 보시면 $(1 - a)^n + \sum_{i=1}^n \alpha (1 - \alpha)^{n-i} = 1$ 이므로 Weight $\alpha$의 합이 1이 됨을 알 수 있습니다. 그렇기 때문에 이것을 Weighted Average이라고 부릅니다. 여기서 Reward $R_i$에 부여되는 Weight $(1 - \alpha)^{n-i}$는 이전 Reward가 많이 누적될수록 기하급수적으로 감소합니다. 따라서 이것을 Exponential Recency-weighted Average 라고도 부릅니다.

이 Step-size parameter는 상황에 따라 변경할 수도 있습니다. Action $a$를 $n$번째 선택했을 때의 Step-size parameter를 $\alpha_n (a)$라고 정의합니다. 만약 $\alpha_n (a) = \frac{1}{n}$으로 설정할 경우 이전에 다루었던 평균과 동일한 식이 됩니다. 이 경우에는 Law of Large number에 의해 실제 Action의 Value에 수렴하지만, 모든 Sequence에 대한 수렴이 보장되지는 않습니다. $\alpha_n (a)$이 수렴하기 위해서는 다음 두 조건을 모두 만족해야 합니다.

\[\sum_{n=1}^{\infty} \alpha_n (a) = \infty \tag{2.7.1}\] \[\sum_{n=1}^{\infty} \alpha^2_n (a) < \infty \tag{2.7.2}\]

식 (2.7.1)은 초기 조건이나 무작위 변동에 상관없이 Step에 따라 충분히 크다는 것을 보장해야 한다는 뜻이고, 식 (2.7.2)는 Step이 수렴할 만큼 충분히 작아지는 것을 보장한다는 뜻입니다. 간단한 예시를 들면, $\alpha_n (a) = \frac{1}{n}$인 경우 두 조건이 모두 충족되므로 수렴하지만, $\alpha_n (a) = \alpha$인 경우 두 번째 조건이 충족되지 않기 때문에 수렴하지 않습니다.

강화학습에서 자주 사용되는 Nonstationary 환경에서는 $\alpha_n (a)$를 정하는 것 또한 하나의 문제가 됩니다. 조건 (2.7.1)과 (2.7.2)를 모두 만족해도 수렴 속도까지 보장하지는 않기 때문입니다. 어떤 경우에는 너무 느리게 수렴할 수도 있기 때문에 적절한 $\alpha_n (a)$이 필요합니다. 이론 부분에서는 이러한 연구 또한 진행되고 있지만, 여기서는 이 부분까지 다루지는 않습니다.

Optimistic Initial Values

지금까지 다루었던 Action에 대한 Value를 추정하는 방법들은 모두 초기 추정치인 $Q_1 (a)$에 상당 부분 의존합니다. 그러므로 이것은 초기 추정치에 의해 Biased되는 위험성이 있습니다. 처음 제안하였던 Sample-average 방법에서는 모든 Action을 한 번 이상 선택하면 Bias가 사라지지만, Step-size parameter를 사용하는 방법에서는 시간이 지남에 따라 감소될지언정 Bias가 사라지지 않습니다. 다만 실제로 이러한 Bias는 일반적으로 크게 문제가 되지 않으며 때때로 오히려 도움이 될 수도 있습니다. 왜냐하면 예상되는 Reward에 대한 대략적인 값을 사전 지식으로 제공할 수도 있기 때문입니다.

Action에 대한 초기 값은 Exploration을 유도하는 방법으로 간단하게 사용할 수 있습니다. 10-armed testbed에서 초기 Action에 대한 Value을 0 대신 5로 설정했다고 가정해봅시다. $q_{*}(a)$는 평균이 0이고 분산이 1인 정규분포에서 선택되었기 때문에 초기 추정치를 5로 설정하는 것은 매우 Optimistic합니다. 쉽게 설명하면, 처음에 어떤 Action을 선택하든 얻게 되는 Reward는 초기 추정치인 5보다 작습니다. 그렇기 때문에 다음 단계에서는 다른 Action을 선택할 가능성이 높고, 추정치가 수렴하기 전까지 모든 Action을 여러 번 선택하게 됩니다. 따라서 초기 추정치를 Optimistic하게 설정한다면 Agent가 Exploration을 많이 하도록 유도할 수 있습니다.

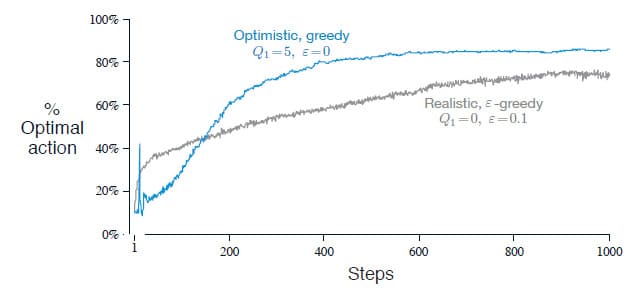
위의 그래프는 10-armed testbed에서 $Q_1 (a) = 5$로 설정한 Greedy 방법과 $Q_1 (a) = 0$으로 설정한 $\epsilon$-greedy 방법의 성능을 비교한 결과입니다. 초기에는 낙관적으로 설정한 Greedy 방법이 Exploration을 더 많이 하기 때문에 성능이 좋지 않지만, 시간이 지남에 따라 Exploration이 감소하기 때문에 결국에는 더 좋은 성능을 보여주고 있습니다.

이러한 간단한 꼼수는 Stationary 문제에 대해 상당히 효과적이지만, 이 방법에서의 Exploration은 결국 일시적이기 때문에 Exploration이 자주 필요한 Nonstationary 문제에서는 별로 도움이 되지 않습니다. 하지만 이러한 꼼수는 구현이 매우 간단하고, 일부이긴 하지만 몇 가지 문제에서 실제로 유용하게 사용할 수 있습니다. 앞으로 이 책에서는 이러한 간단한 꼼수들을 몇 개 더 소개할 예정입니다.

Upper-Confidence-Bound Action Selection

Action에 대한 Value를 추정하는 것은 정확성이 보장되지 않기 때문에 꾸준한 Exploration이 필요합니다. Greedy 방법은 현재 가장 좋아보이는 Action을 선택하지만 실제로 다른 Action이 더 가치가 높을 수도 있기 때문입니다. $\epsilon$-greedy 방법은 낮은 확률로 무작위 Action을 선택하지만, 이 무작위성 때문에 Exploration이 부족하여 추정하지 못했던 Action이나 추정값이 최대값으로 예상되는 Action을 따로 고려하지 않습니다. 이런 특수한 경우를 고려하기 위해 다음과 같은 방법을 생각해볼 수 있습니다.

\[A_t \doteq \underset{a}{\operatorname{argmax}} \ \left[ Q_t (a) + c \sqrt{\ln t \over N_t (a)} \, \right] \tag{2.10}\]

$N_t (a)$는 시간 $t$까지 Action $a$를 선택한 횟수이고 $c > 0$는 Exploration의 정도를 나타내는 상수입니다. $N_t (a)$가 만약 0이라면, $a$는 가장 가치가 큰 Action으로 취급됩니다.

이러한 방법을 Upper Confidence Bound (UCB)라고 부르며 제곱근 항은 Action $a$에 대한 추정값의 불확실성, 또는 분산의 척도를 의미합니다. 즉, 이것의 최대값은 Action의 가치에 대한 상한선으로 볼 수 있으며 $c$는 신뢰 수준을 결정합니다. $a$가 선택될 때마다 $N_t (a)$가 증가하므로 (=분모가 증가하므로) 불확실성이 감소된다고 볼 수 있습니다. 반면에 다른 Action이 선택된다면 $t$가 증가하므로 (=분자가 증가하므로) 불확실성이 증가됩니다. 즉, 이것은 자주 선택된 Action을 또 다시 선택하는 빈도를 줄이면서 모든 Action을 선택할 수 있는 방법이라고 볼 수 있습니다.

위의 그래프는 10-armed testbed에서 UCB를 사용한 결과입니다. 그래프에서는 UCB가 잘 수행되는 것으로 보이지만, 이 책에서 다룰 일반적인 강화학습에 확장하기에는 어렵습니다. 대표적으로 계속 언급하고 있는 Nonstationary 문제나, State가 매우 많은 경우에는 적용할 수 없으므로 이런 방법도 있다 정도만 이해하고 넘어가시면 되겠습니다.

Gradient Bandit Algorithms

지금까지는 Action을 선택할 때 Action의 Value를 추정하는 방법을 사용하였습니다. 이번에는 Action을 선택하는 또 다른 방법을 하나 소개하려고 합니다. 여기서는 각 Action $a$에 대한 Preference $H_t (a) \in \mathbb{R}$를 사용합니다. Preference가 높을 수록 해당 Action이 더 많이 선택되지만, 이것이 많은 Reward를 받는다는 뜻은 아닙니다. 단지 어떤 Action이 다른 Action에 비해 상대적으로 Preference가 높은지만을 나타내는 지표입니다. 모든 Action의 Preference에 1000을 더하면 확률에 영향이 없으며, 다음과 같이 Soft-max 분포로 나타납니다. (Soft-max 분포는 Gibbs, 또는 Boltzmann 분포라고도 부릅니다)

\[Pr \left\{ A_t = a \right\} \doteq \frac{e^{H_t (a)}}{\sum_{b=1}^k e^{H_t (b)}} \doteq \pi_t (a) \tag{2.11}\]

$\pi_t (a)$는 시간 $t$에서 Action $a$를 선택할 확률을 의미합니다. 식 (2.11)에서 처음에는 모든 Action에 대해 Preference가 동일하므로(즉, 모든 $a$에 대해 $H_1 (a) = 0$) 모든 Action이 선택될 확률은 동일합니다.

Stochastic Gradient Ascent를 기반으로 하는 Soft-max Action Preference를 학습하는 알고리즘이 있습니다. 각 단계에서 Action $A_t$를 선택하고 Reward $R_t$를 받은 후, Action에 대한 Preference는 다음과 같이 업데이트됩니다.

\[H_{t+1} (A_t) \doteq H_t (A_t) + \alpha (R_t - \bar{R}_t) (1 - \pi_t (A_t) \qquad \text{and} \tag{2.12.1}\] \[H_{t+1} (a) \doteq H_t (a) - \alpha (R_t - \bar{R}_t) \pi_t (a) \qquad \text{for all} \ a \neq A_t \tag{2.12.2}\]

여기서 $\alpha > 0$은 이전에 언급했던 Step-size parameter이고, $\bar{R}_t \in \mathbb{R}$는 시간 $t$를 제외된 평균 보수입니다. (단, $\bar{R}_1 \doteq R_1$) $\bar{R}_t$의 계산법은 Incremental Implementation이나 Tracking a Nonstationary Problem에서 설명한 것과 동일합니다. $\bar{R}_t$의 역할은 Reward가 상대적으로 얼마나 높은지를 측정하는 Baseline 역할을 합니다. Reward가 Baseline보다 높으면 미래에 $A_t$를 선택할 확률이 증가하고, Baseline보다 낮으면 확률이 감소하는 방식입니다. 선택한 Action은 식 (2.12.1)로, 선택하지 않은 Action은 식 (2.12.2)로 계산됩니다.

위의 그래프는 10-armed testbed에서 Gradient bandit 알고리즘의 결과를 나타냅니다. 여기서 $q_*(a)$는 평균이 4, 분산이 1인 정규분포에 따라 선택되었습니다. Reward의 평균을 올려도 새로운 Reward가 바로 반영되는 Baseline으로 인해 Gradient bandit 알고리즘에 전혀 영향을 끼치지 않습니다. 하지만 만약 Baseline을 제외한다면(즉, $\bar{R}_t = 0$) 그래프에서 보여주는 것처럼 성능이 크게 저하됩니다.

Contextual Bandits

지금까지는 현재 하고 있는 학습을 다른 상황이나 작업과 연관시킬 필요가 없는 경우만 고려했습니다. 즉, Agent가 고정된 최대 Reward를 얻는 Action(Stationary인 경우)을 찾거나, 시간이 지남에 따라 변경되는 최적의 Action(Nonstationary인 경우)을 찾기 위해 노력했습니다. 그러나 일반적인 강화학습에서는 여러 상황이나 환경이 주어질 수 있으며, 이 때는 Policy 자체를 학습할 필요가 있습니다.

예를 들어, 몇 가지 다른 $k$-armed bandit 작업이 있고 각 단계에서 무작위로 하나만 선택한다고 가정합니다. 따라서 단계마다 선택되는 작업은 무작위로 변경됩니다. 각 작업이 선택되는 확률이 (시간이 지남에 따라) 변경되지 않으면 그냥 단일 Stationary $k$-armed bandit 작업과 동일합니다. 하지만 여기서는 작업이 선택될 때 어떻게 바뀌었는지 알 수 있는 힌트가 주어진다고 가정해봅시다. 슬롯머신으로 치면 슬롯머신 화면의 색이 변하는 것처럼 말입니다. 빨간색 화면이 나오면 첫 번째 레버를 선택하고, 초록색 화면이 나오면 두 번째 레버를 선택한다라는 식으로 결정하는 것이 바로 Policy를 학습하는 것입니다.

이렇게 최적의 Action을 검색하기 위해 Trial-and-error와 주어진 상황을 Association시키는 작업이 포함되기 때문에 Associative Search이라고 부릅니다. Associative Search는 또 다른 말로 Contextual Bandits라고도 부릅니다. Associative Search는 $k$-armed bandit 문제와 전체 강화학습 문제의 중간에 위치해 있습니다. Policy에 대한 학습을 포함한다는 점에서 강화학습과 비슷하지만, 각 Action이 즉각적인 Reward에만 영향을 미친다는 점에서 $k$-armed bandit 문제와 같습니다. Action이 Reward 뿐만 아니라 다음 상황에 영향을 미치도록 설정한다면 강화학습이라고 말할 수 있습니다. 다음 장에서 이에 대해 더 자세히 알아보도록 하겠습니다.

Summary

2장에서는 Exploration과 Exploitation의 균형을 맞추는 간단한 방법들을 몇 가지 소개했습니다.

• $\epsilon$-greedy 방법은 낮은 확률로 무작위 Action을 선택함으로써 Exploration을 합니다.
• UCB 방법은 적게 선택된 Action이 선택될 확률을 높임으로써 Exploration을 합니다.
• Gradient bandit 알고리즘은 각 Action에 대한 Value 대신 Preference를 추정하여 Exploration을 합니다.
• 초기값을 Optimistic하게 설정하는 간단한 방법으로 간단한 Exploration이 가능합니다.

이 방법들 중 어느 것이 가장 좋은지 판단하기는 어렵습니다. $k$-armed testbed 문제에서 같은 방법을 사용했더라도 Step-size parameter가 달라지면 성능의 차이가 확연히 드러났습니다. 따라서 여기서는 보기 쉽도록 각 방법마다 적절한 매개변수 구간에서 1000 단계가 지났을 때의 결과만 비교해보도록 하겠습니다.

이 성능 비교에서 재밌는 점은 모든 방법이 Convex하다는 것입니다. 또한 각 방법마다 Step-size parameter를 중간 정도로 설정하는 것이 가장 뛰어난 성능을 보인다는 것도 알 수 있습니다.

교재에서는 $k$-armed bandit 문제를 해결하는 또 다른 방법으로 Gittins index 같은 것도 소개했지만, 내용상 중요한 부분이 아니라고 생각했기 때문에 여기에서는 생략하도록 하겠습니다.

2장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!