On-policy Control with Approximation

지난 장에서 근사를 이용한 Value Function Approximation에 대해 알아보았습니다. 이번 장에서는 매개변수를 사용하여 Action-Value Function $\hat{q}(s, a, \mathbf{w}) \approx q_* (s, a)$를 근사하는 Control 문제를 다루겠습니다. (Weight Vector $\mathbf{w} \in \mathbb{E}^d$는 유한 차원 Vector입니다) 이번 장에서는 먼저 On-policy에만 집중하고, Off-policy의 문제는 다음 장에서 다룰 예정입니다.

가장 먼저 지난 장에서 다룬 Semi-gradient TD(0)를 확장한 Semi-gradient Sarsa 알고리즘을 다룹니다. Episodic Task에서는 이 확장이 간단하지만, Continuing Task에서는 Optimal Policy를 찾기 위해 Discounting을 다시 사용해야 합니다. 신기한 점은, 진짜 Function Approximation을 얻게 되면 Discounting을 버리고 새로운 Differential Value Function을 사용하여 Control 문제를 새로운 Average-reward 식으로 바꿔야 합니다.

Episodic Task에서는 먼저 지난 장에서 다룬 함수 근사를 State-Value에서 Action-Value로 확장합니다. 그런 다음 $\epsilon$-greedy를 사용한 Action 선택을 통해 On-policy GPI의 일반적인 패턴을 따라 Control하도록 확장합니다. 그 후 Mountain Car 예제에서 $n$-step Linear Sarsa가 어떤 성능을 보이는지 결과를 확인하고, Continuing Task로 넘어가는 순서로 진행하겠습니다.

Episodic Semi-gradient Control

먼저 지난 장에서 배운 Semi-gradient Prediction을 Action-Value로 확장해보겠습니다. 이 경우 Weight Vector $\mathbf{w}$를 매개변수로 사용하여 Action-Value Function으로 표현한다면 $\hat{q} \approx q_{\pi}$가 됩니다. $S_t \mapsto U_t$ 형태의 무작위 Training Data를 고려하기 전에, $S_t, A_t \mapsto U_t$ 형태의 데이터를 먼저 살펴보겠습니다. Update의 Target인 $U_t$는 Monte Carlo의 Return $G_t$나 $n$-step Sarsa의 Return 식 (7.4)와 같이 일반적인 Backed-up 값을 포함하여 $q_{\pi} (S_t, A_t)$의 근사값이 될 수 있습니다. Action-Value 예측을 위한 일반적인 Gradient Descent Update는 다음과 같습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ U_t - \hat{q} (S_t, A_t, \mathbf{w}_t) \right] \nabla \hat{q} (S_t, A_t, \mathbf{w}_t) \tag{10.1}\]

이것을 1-step Sarsa 방법에 맞게 수정하면 다음과 같습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ R_{t+1} + \gamma \hat{q}(S_{t+1, A_{t+1}, \mathbf{w}_t}) - \hat{q} (S_t, A_t, \mathbf{w}_t) \right] \nabla \hat{q} (S_t, A_t, \mathbf{w}_t) \tag{10.2}\]

이 Update 식을 사용한 Control 방법을 Episodic Semi-gradient 1-step Sarsa라고 부릅니다. 고정된 Policy의 경우 이 방법은 TD(0)와 동일한 방식으로 수렴하며, 식 (9.14)와 동일한 Error Bound를 가집니다.

Control 방법을 제대로 구축하기 위해서는 이러한 Action-Value Approximation을 Policy Improvement 및 Action 선택을 위한 방법들과 융합해야 합니다. 하지만 Continuous Action이나 수가 매우 많은 Discrete Action이 주어졌을 때 사용할 수 있는 적절한 기술은 현재도 연구가 이루어질 정도로 아직 명확한 방법이 없습니다. 다행히 Action 집합이 이산적이고 그 수가 적절하다면 이전 장에서 소개한 방법을 도입할 수 있습니다. 즉, 다음 State $S_{t+1}$에서 사용 가능한 Action에 대해 $\hat{q}(S_{t+1}, a, \mathbf{w}_t)$를 계산하면 Greedy Action인 $A_{t+1}^* = \underset{a}{\operatorname{argmax}} \hat{q} (S_{t+1}, a, \mathbf{w}_t)$를 구할 수 있습니다. 그 후 $\epsilon$-greedy와 같은 Softmax 방법을 통해 Policy Improvement를 수행할 수 있습니다. 이 알고리즘의 전체 Pseudocode는 다음과 같습니다.

Example 10.1) Mountain Car Task

아래 그림의 왼쪽 위를 보시면 자동차가 가파른 산길을 통과하려고 합니다. 그런데 이 자동차는 동력이 부족하기 때문에 단순히 엔진의 힘으로는 Goal 지점에 도달할 수 없고, 유일한 해결책은 반대방향으로 먼저 자동차를 후진한 다음 가속도와 관성을 이용해 Goal 지점에 도달하는 것입니다. 이 예제는 목표에 도달하기 위해 오히려 목표에서 멀어져야 하는 Control 문제입니다. 많은 기존의 Control 방법들은 명시적으로 이러한 문제의 해결 방법을 지원하지 않는 한 해결하기 쉽지 않습니다.

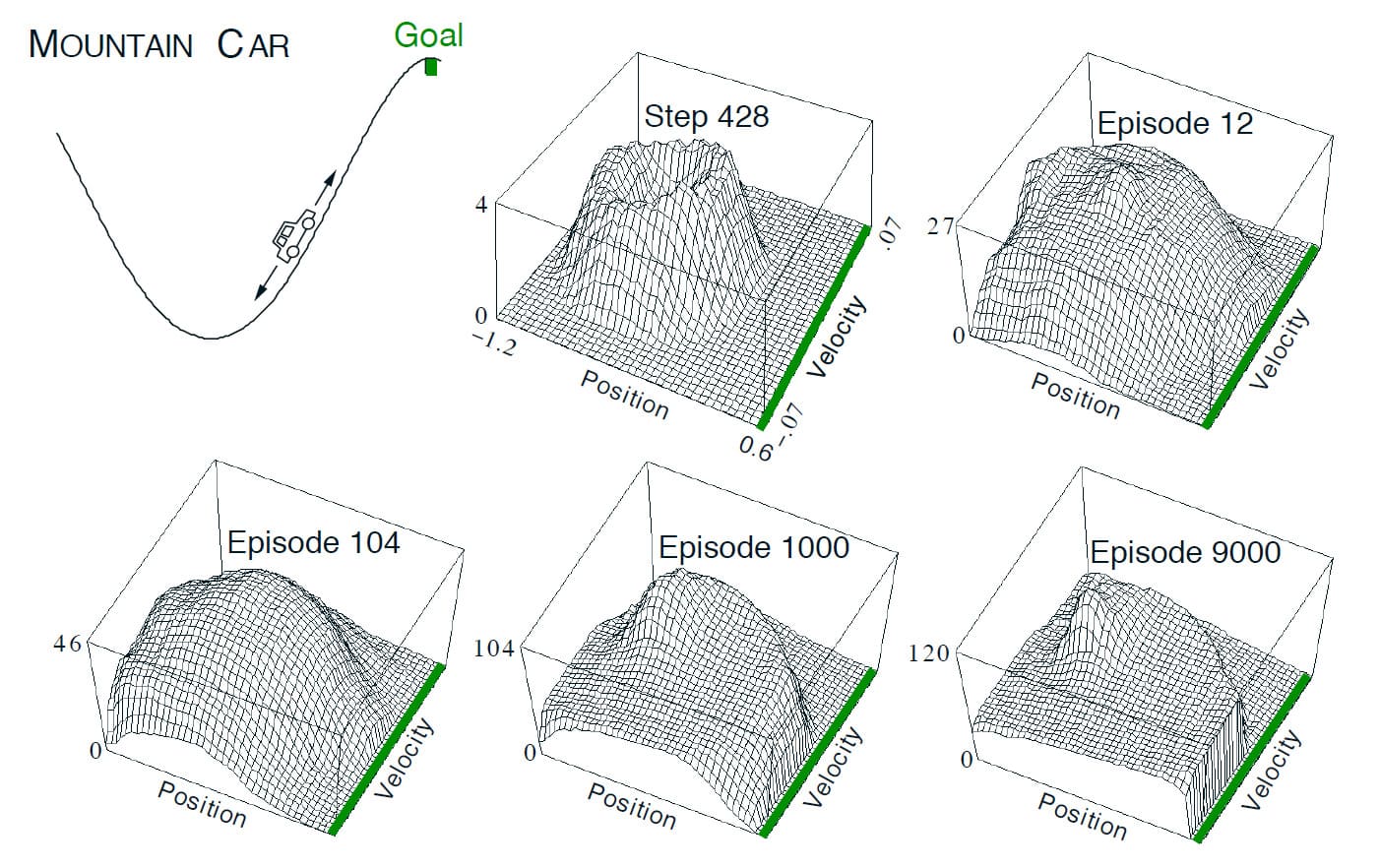
Mountain Car 문제에서 Reward는 자동차가 Goal 위치를 지나갈 때까지(=Episode가 종료될 때까지) 모든 시간 단계에서 -1로 정의되어 있습니다. 자동차가 선택할 수 있는 Action은 3개로, 전진(+1), 후진(-1) 및 정지(0)입니다. 자동차는 단순한 물리 법칙에 따라 움직이며, 자동차의 위치 $x_t$ 및 속도 $\dot{x}_t$는 다음과 같이 Update됩니다.

\[\begin{align} x_{t+1} & \doteq \text{bound} \left[ x_t + \dot{x}_{t+1} \right] \\ \\ \dot{x}_{t+1} & \doteq \text{bound} \left[ \dot{x}_t + 0.001 A_t - 0.0025 \cos (3x_t) \right] \end{align}\]

위 식에서 $\text{bound}$ 연산은 위치와 속도가 $-1.2 \le x_{t+1} \le 0.5$ 및 $-0.07 \le \dot{x}_{t+1} \le 0.07$ 구간을 벗어나지 않게 만드는 연산입니다. 또한, $x_{t+1}$이 왼쪽 경계에 도달하면 $\dot{x}_{t+1}$는 0으로 재설정됩니다. 만약 오른쪽 경계에 도달하면 Goal 지점에 도달한 것이니 Episode가 종료됩니다. 각각의 Episode는 임의의 위치 $x_t \in \left[ -0.6, -0.4 \right)$에서 속도 0으로 시작합니다. 위치와 속도는 모두 Continuous State이므로 이를 Binary Feature로 변환하기 위해 Tile Coding을 사용하였습니다. Tile Coding에 의해 생성된 Feature Vector $\mathbf{x} (s, a)$는 Action-Value Function를 근사화하기 위해 다음과 같이 Weight Vector와 선형으로 결합되었습니다.

\[\hat{q} (s, a, \mathbf{w}) \doteq \mathbf{w}^{\sf T} \mathbf{x} (s, a) = \sum_{i=1}^d w_i \cdot x_i (s, a) \tag{10.3}\]

위의 그림은 이 함수 근사로 Mountain Car 문제를 해결하는 방법을 학습하는 동안 발생하는 일을 나타내고 있습니다. 그래프는 단일 실행에서 학습된 Value Function의 부호를 뒤집은 결과입니다. 초기의 Action Value는 모두 0이었습니다. 모든 Action에 대한 Reward가 음수이기 때문에 Action Value를 낙관적으로 본 것이며, 이것을 통해 $\epsilon = 0$일지라도 탐색이 일어나도록 유도한 것입니다. 그림 중간에 428단계에서는 한 Episode도 완료되지 않았지만 자동차는 State 공간에서 궤도를 따라 앞뒤로 움직였습니다. 자주 방문하는 모든 State는 그렇지 않은 State보다 더 나쁘게 평가되고, 실제 Reward 또한 예상했던 것보다 나빴기 때문입니다. 이는 해법을 찾을 때까지 자동차가 있던 곳에서 계속 멀어져 새로운 State를 탐색하도록 유도합니다.

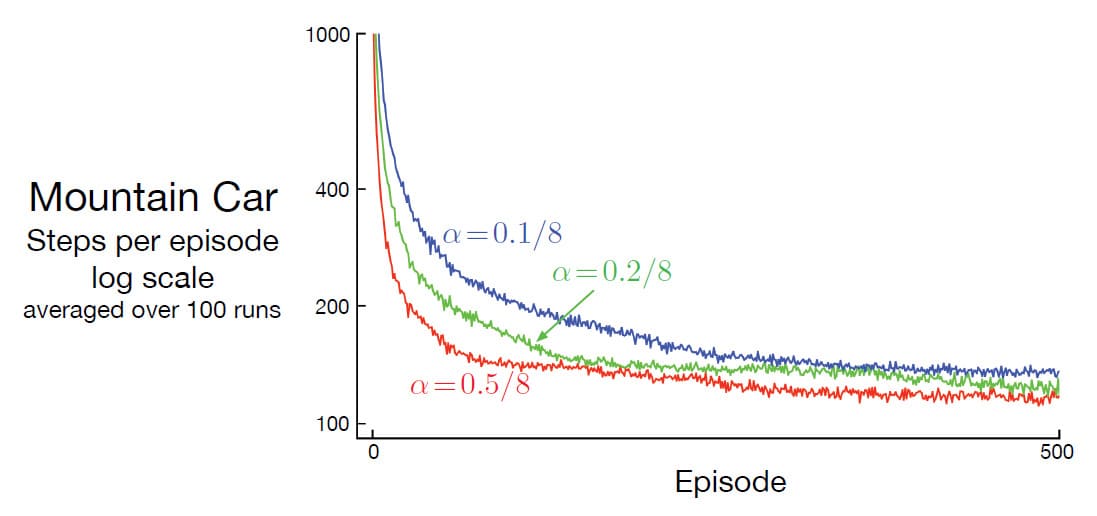
위 그래프는 다양한 Step-size에 대해 Mountain Car 문제에서 Semi-gradient Sarsa의 학습 곡선을 보여줍니다.

□

Semi-gradient $n$-step Sarsa

Semi-gradient Sarsa의 $n$-step 버전의 Return만 구하면 식 (10.1)의 Update 식을 그대로 사용하여 계산할 수 있습니다. $n$-step 버전의 Return은 식 (7.4)를 함수 근사 형식으로 일반화하면 다음과 같이 변형할 수 있습니다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots +  \gamma^{n-1} R_{t+n} + \gamma^n \hat{q} (S_{t+n}, A_{t+n}, \mathbf{w}_{t+n-1}), \quad t+n < T \tag{10.4}\]

식 (7.4)와 마찬가지로 $t + n \ge T$라면 $G_{t:t+n} \doteq G_t$입니다. $n$-step Update는 식 (10.1)과 크게 다르지 않습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ G_{t:t+n} - \hat{q} (S_t, A_t, \mathbf{w}_t) \right] \nabla \hat{q} (S_t, A_t, \mathbf{w}_t), \quad 0 \le t < T \tag{10.5}\]

Semi-gradient $n$-step Sarsa의 전체 알고리즘은 다음과 같습니다.

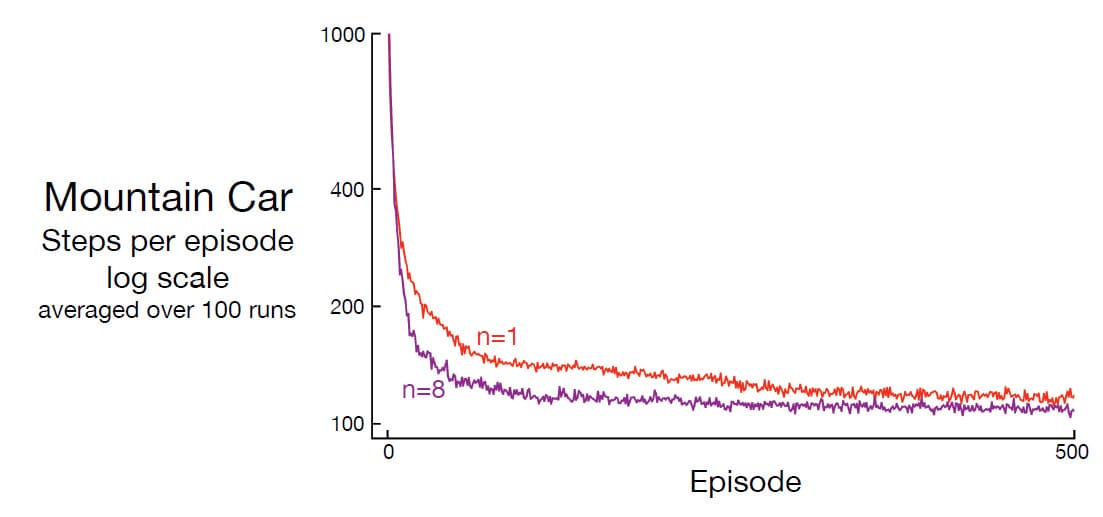
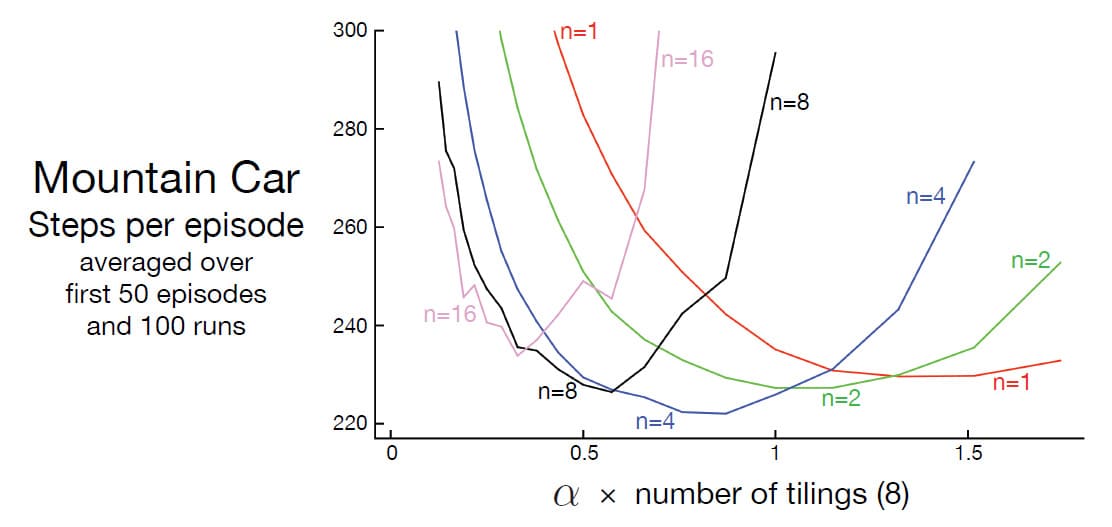
7장에서 언급한 것과 마찬가지로 $n$이 1보다 크면서 중간 단계만큼 Bootstrapping 하는 경우 성능이 가장 좋습니다. 아래 그림은 $n=8$이 $n=1$보다 더 빨리 학습하는 것을 보여줍니다. 또한 그 아래 그림은 이 문제에서 매개변수 $\alpha$와 $n$이 학습에 어떠한 영향을 끼치는지 나타냅니다.

Average Reward: A New Problem Setting for Continuing Tasks

이번 Section에서는 Continuing Task로 넘어가겠습니다. Continuing Task는 Episodic Task와 다르게 종료되지 않고 영원히 계속되는 문제이므로 Return을 다른 방법으로 계산합니다. 대표적으로 Average Reward 방법이 있습니다. Average Reward 방법에서 Policy $\pi$의 우수함은 Average Rate of Reward, 또는 단순히 Average Reward로 정의되며, 다음과 같이 $r(\pi)$로 표현되는 Policy를 따릅니다.

\[\begin{align} r(\pi) & \doteq \lim_{h \to \infty} \frac{1}{h} \sum_{t=1}^h \mathbb{E} \left[ R_t | S_0, A_{0:t-1} \sim \pi \right] \tag{10.6} \\ \\ &= \lim_{t \to \infty} \mathbb{E} \left[ R_t | S_0, A_{0:t-1} \sim \pi \right] \tag{10.7} \\ \\ &= \sum_s \mu_{\pi} (s) \sum_a \pi (a|s) \sum_{s', r} p(s', r | s, a) r \end{align}\]

위 식에서의 기대값은 초기 State $S_0$와 Policy $\pi$를 따르는 Action $A_0, A_1, \ldots, A_{t-1}$에 따라 정해집니다. 두 번째 및 세 번째 식은 Steady-state Distribution $\mu_{\pi} (s) \doteq \underset{t \to \infty}{\operatorname{lim}} \text{Pr} \{ S_t = s \mid A_{0:t-1} \sim \pi \}$가 존재하고 $S_0$에 독립적일 때 성립합니다. 즉, MDP가 Ergodic 할 때 성립합니다. Ergodic MDP에서 시작 State와 Agent가 초기에 내린 선택은 일시적인 효과만 있습니다. 장기적으로 어떤 State에 있을지는 Policy와 MDP의 Transition Probability에만 영향을 받습니다. Ergodicity는 충분조건이지만, 식 (10.6)에서 극한의 존재를 보장할 필요는 없습니다.

Discounting이 없는 Continuing Task의 경우 Optimality의 종류에 따라 약간의 차이가 있습니다. 하지만 대부분 실용적인 목적을 위해서는 시간 단계당 Average Reward, 즉 $r(\pi)$에 맞춰 Policy를 따르는 것이 적절합니다. 이것은 식 (10.7)에서 보여주는 $\pi$의 Average Reward, 또는 Reward Rate입니다. 여기서는 $r(\pi)$의 최대값을 달성하는 모든 Policy를 Optimal Policy로 간주하도록 하겠습니다.

Steady-state Distribution $\mu_{\pi}$는 Policy $\pi$에 따라 Action을 선택하면 동일한 Distribution을 유지하는 특수한 Distribution입니다. 수학적으로는 다음과 같이 표현합니다.

\[\sum_s \mu_{\pi} (s) \sum_a \pi(a|s) p(s'|s, a) = \mu_{\pi} (s') \tag{10.8}\]

Average Reward 방법에서 Return은 Reward와 Average Reward 간의 차이로 정의됩니다.

\[G_t \doteq R_{t+1} - r(\pi) + R_{t+2} - r(\pi) + R_{t+3} - r(\pi) + \cdots \tag{10.9}\]

식 (10.9)와 같은 Return을 Differential Return이라고 하며, 이것을 사용한 Value Function을 Differential Value Function이라고 합니다. 기존 Value Function이 Discounted Return으로 정의된 것처럼 Differential Value Function 또한 새로운 Return의 관점에서 정의됩니다. 따라서 기존과 마찬가지로 Differential Value Function에서도 $v_{\pi} (s) \doteq \mathbb{E}_{\pi} \left[ G_t \mid S_t = s \right]$, $q_{\pi} (s, a) \doteq \mathbb{E}_{\pi} \left[ G_t \mid S_t = s, A_t = a \right]$와 같은 동일한 표기법을 사용할 것입니다. Differential Value Function에서도 Bellman Equation이 있는데, 이것은 이전에 다룬 것과 약간 다릅니다. 간단하게 설명하면, $\gamma$를 모두 제거하고 모든 Reward를 Reward와 실제 Average Reward 간의 차이로 대체합니다.

\[\begin{align} v_{\pi} (s) &= \sum_a \pi(a|s) \sum_{r, s'} p(s',r|s, a) \left[ r - r(\pi) + v_{\pi} (s') \right] \\ \\ q_{\pi} (s, a) &= \sum_{r, s'} p (s', r | s, a) \left[ r - r(\pi) + \sum_{a'} \pi (a'|s') q_{\pi} (s', a') \right] \\ \\ v_* (s) &= \max_a \sum_{r, s'} p(s', r|s, a) \left[ r - \max_{\pi} r(\pi) + v_* (s') \right] \\ \\ q_* (s, a) &= \sum_{r, s'} p(s', r | s, a) \left[ r - \max_{\pi} r(\pi) + \max_{a'} q_* (s', a') \right] \end{align}\]

마찬가지로 Differential TD Error 또한 다음과 같이 변경됩니다.

\[\begin{align} \delta_t & \doteq R_{t+1} - \bar{R}_t + \hat{v}(S_{t+1}, \mathbf{w}_t) - \hat{v}(S_t, \mathbf{w}_t) \tag{10.10} \\ \\ \delta_t & \doteq R_{t+1} - \bar{R}_t + \hat{q}(S_{t+1}, A_{t+1}, \mathbf{w}_t) - \hat{q}(S_t, A_t, \mathbf{w}_t) \tag{10.11} \end{align}\]

여기서 $\bar{R}_t$는 시간 단계 $t$에서 Average Reward $r(\pi)$를 추정한 값입니다. 이렇게 변형된 식을 알고리즘에 대입하기만 하면 이론적으로 큰 문제 없이 Average Reward에 대한 방법으로 바꿀 수 있습니다. 예를 들어, Semi-gradient Sarsa의 Average Reward 버전은 식 (10.2)를 다음과 같이 변경하면 됩니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w} + \alpha \delta_t \nabla \hat{q} (S_t, A_t, \mathbf{w}_t) \tag{10.12}\]

식 (10.12)에서 $\delta_t$는 식 (10.11)과 같습니다. Differential Semi-gradient Sarsa 알고리즘의 완전한 Pseudocode는 아래와 같습니다.

이 알고리즘의 한 가지 문제점은 Differential Value로 수렴하지 않고 Differential Value에 임의의 Offset을 더한 값으로 수렴된다는 것입니다. 위에서 언급한 Bellman Equation과 TD Error는 모든 값이 같은 양만큼 변화해도 영향을 받지 않습니다. 따라서 Offset은 실제로 중요하지 않을 수 있지만, 이 Offset을 제거하기 위한 연구는 지금도 이루어지고 있습니다.

Example 10.2) An Access-Control Queuing Task

이 예제는 10개의 서버 집합에 대해 접근 제어와 관련된 결정 문제입니다. 이용자는 4가지 종류의 우선순위로 분류된 작업을 단일 Queue에 보냅니다. 서버에 대한 접근 권한이 부여되면 이용자는 우선 순위에 따라 서버에 1, 2, 4 또는 8의 비용을 지불하는데, 우선 순위가 높은 이용자는 더 많은 비용을 지불합니다. 각 시간 단계에서 Queue 맨 앞에 있는 이용자는 Accept (서버 중 하나에 할당)되거나 Reject (대기열에서 0의 Reward를 받고 제거) 됩니다. 어떤 결과가 나오든 다음 이용자의 순서로 넘어갑니다. Queue는 절때 비지 않고, Queue에 있는 이용자의 우선 순위는 무작위로 분포되어 있다고 가정합니다. 물론 여유있는 서버가 없다면 이용자의 요청은 모두 거부됩니다. 사용 중인 서버는 각각의 시간 단계에서 확률 $p = 0.06$에 따라 다시 여유 State로 돌아옵니다. 이용자의 도착 및 출발 통계는 알 수 없다고 가정하겠습니다. 이 문제의 목적은 이용자의 우선 순위와 여유 State의 서버 수에 따라 요청을 Accept할지, Reject 할지를 결정하는 것입니다. 즉, 장기적인 Reward를 극대화하는 것입니다.

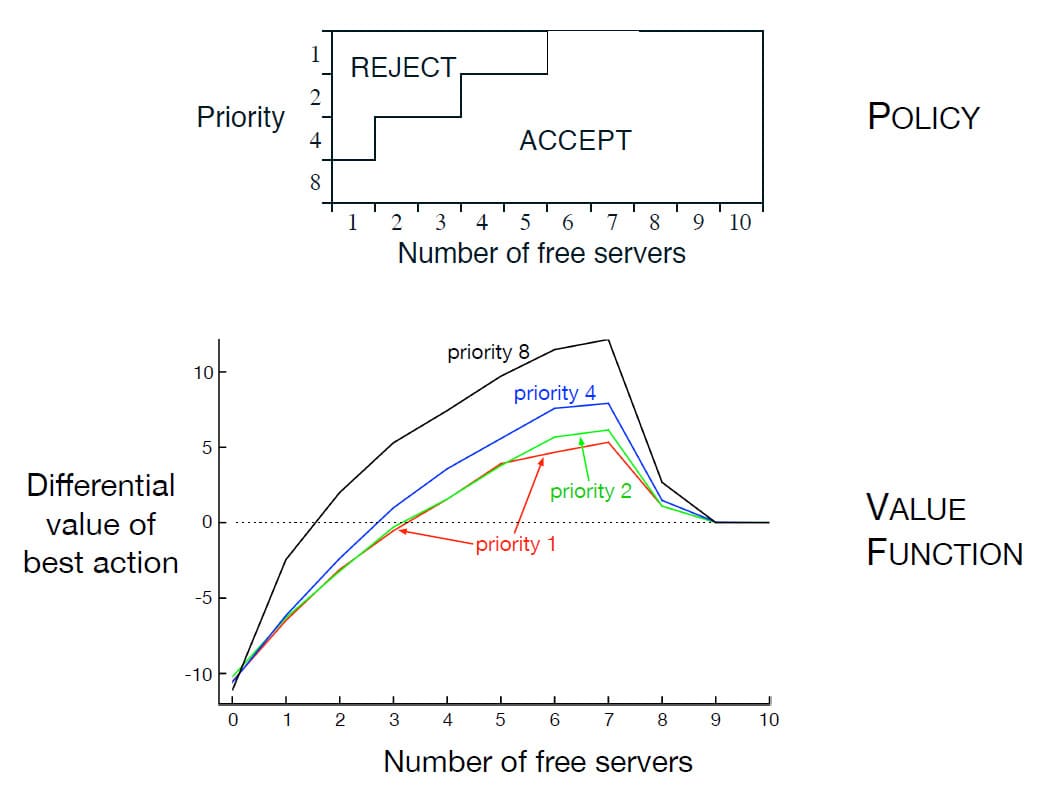
교재에서는 이 문제를 Tabular 방식으로 해결하였습니다. State 간의 일반화는 없지만, 일반적인 함수 근사를 사용할 수는 있습니다. 따라서 각 State의 쌍(여유 State의 서버 수와 맨 앞에 있는 이용자의 우선 순위)과 Action(Accept 또는 Reject)에 대해 Differential Action-Value Function을 추정합니다. 위의 그림은 $\alpha = 0.01$, $\beta = 0.01$, $\epsilon = 0.1$로 설정한 Differential Semi-gradient Sarsa 해법을 보여줍니다. 초기의 Action-Value와 $\bar{R}$은 0으로 설정하였습니다.

□

Deprecating the Discounted Setting

Continuing, Discounted Task에서는 각 State의 Return을 개별적으로 구분할 수 있는 Tabular에서 매우 유용했습니다. 하지만 근사를 사용하는 경우에는 Tabular에서 생각하지 못했던 여러 문제점이 발생하게 됩니다.

예를 들어, 시작이나 끝이 없고 State를 제대로 식별하지 못하는 무한 Return을 가정해봅시다. 각 State는 Feature Vector로만 표시할 수 있기 때문에 State를 구별하는 데 거의 도움이 되지 않습니다. 어떤 경우에는 모든 Feature Vector가 동일할 수도 있습니다. 따라서 Reward에 대한 순서만 주어지고 성능은 이러한 순서로만 평가될 수 있습니다.

이 문제를 해결하는 방법 중 하나는 장기간에 걸쳐 Reward를 평균화하는 것입니다. 이것이 이전 Section에서 다룬 Average Reward의 아이디어입니다. 만약 Discount를 사용하고 싶다면 각 시간 단계에 대해 Discount된 Return을 측정할 수 있는데, 어떤 Return은 크고 어떤 Return은 작을 수 있으므로 충분히 긴 시간 단계에 걸쳐 평균을 내야 합니다. 그런데 간단히 생각해보면 결국 Discounted Return의 평균이 Reward의 평균에 비례한다는 것을 알 수 있습니다. 수학적으로 따져봐도 Policy $\pi$에 대해 Discounted Return의 평균은 $r(\pi) / ( 1 - \gamma)$입니다. 즉, 사실상 $r(\pi)$나 마찬가지입니다. 따라서 Discounted Return의 평균에서 Policy의 Ordering은 Average Reward에서와 동일하므로, Discount Factor $\gamma$는 문제에 영향을 끼치지 않습니다. Discount Factor는 $0 \le \gamma < 1$이기 때문입니다.

이것을 엄밀하게 증명하기 전에, 먼저 직관적으로 간단하게 설명하겠습니다. (State를 제대로 식별하지 못하기 때문에) 각각의 시간 단계가 다른 모든 시간 단계와 동일하다고 가정해보겠습니다. Discount를 사용한 시간 단계 $t$의 Reward는 시간 단계 $t-1$의 Return에서 Discount를 사용하지 않은채 나오고, 시간 단계 $t-2$의 Return에서 1번 Discount 되며, 같은 이치로 시간 단계 $t-1000$의 Return에서 999번 Discount 됩니다. 따라서 시간 단계 $t$에서 Reward의 Weight는 $1 + \gamma + \gamma^2 + \gamma^3 + \cdots = 1/(1-\gamma)$가 됩니다. 모든 State가 동일하기 때문에 모든 State에 대해 이 Weight가 곱해지므로 Reward의 평균은 $r(\pi) / ( 1 - \gamma)$가 됩니다.

The Futility of Discounting in Continuing Problems

이 부분에서는 Policy $\pi$에 따른 Discounted Value의 합이 어떻게 Average Reward 방법과 동일한지 수학적으로 식을 전개하도록 하겠습니다. Discounted Value Function을 $v_{\pi}^{\gamma}$라고 하면,

\[\begin{align} J(\pi) &= \sum_s \mu_{\pi} (s) v_{\pi}^{\gamma} (s) \\ \\ &= \sum_s \mu_{\pi}(s) \sum_a \pi (a|s) \sum_{s'} \sum_{r} p (s', r | s, a) \left[ r + \gamma v_{\pi}^{\gamma} (s') \right] \tag{Bellman Eq.} \\ \\ &= r(\pi) + \sum_s \mu_{\pi} (s) \sum_a \pi (a|s) \sum_{s'} \sum_r p (s', r | s, a) \gamma v_{\pi}^{\gamma} (s') \tag{from (10.7)} \\ \\ &= r(\pi) + \gamma \sum_{'s} v_{\pi}^{\gamma} (s') \sum_s \mu_{\pi} (s) \sum_a \pi (a|s) p (s' | s, a) \tag{from (3.4)} \\ \\ &= r(\pi) + \gamma \sum_{s'} v_{\pi}^{\gamma} (s') \mu_{\pi} (s') \tag{from (10.8)} \\ \\ &= r(\pi) + \gamma J(\pi) \\ \\ &= r(\pi) + \gamma r(\pi) + \gamma^2 J(\pi) \\ \\ &= r(\pi) + \gamma r(\pi) + \gamma^2 r(\pi) + \gamma^3 r(\pi)  + \cdots \\ \\ &= \frac{1}{1 - \gamma} r(\pi) \end{align}\]

즉, Discounted Value Function은 Discount되지 않은 Average Reward와 동일한 Policy를 생성하므로, Discount Factor $\gamma$는 영향을 끼치지 않는 것을 알 수 있습니다.

□

이 증명은 결국 On-policy Distribution에서 Discounted Value를 최적화하는 것과 Undiscounted Average Reward를 최적화 하는 것이 동일하다는 것을 의미합니다. $\gamma$가 실제로 어떤 값이든 상관이 없습니다. 즉, 이것은 함수 근사의 Control 문제에서 Discount가 아무런 역할을 하지 않는다는 것을 보여줍니다. 그럼에도 불구하고 Discount를 사용할 수 없는 것은 아닙니다. Discount Factor $\gamma$를 문제의 매개변수에서 해법의 매개변수로 바꾸면 됩니다. 하지만 그렇게 할 시 함수 근사를 사용하는 Discounting 알고리즘은 On-policy Distribution에서 Discounted Value를 최적화하지 않으므로 Average Reward를 최적화한다고 보장할 수 없습니다.

Discount를 사용한 Control이 어려운 이유는 함수 근사를 사용하게 되면 Policy Improvement Theorem를 사용할 수 없기 때문입니다. 즉, State의 Discounted Value를 개선하기 위해 Policy를 변경하면 전체 Policy를 개선할 수 있다는 정리가 통용되지 않습니다. 이 정리는 지금까지의 강화학습 Control의 핵심 이론이었으나, 함수 근사를 사용함으로써 이 정리를 사용하는 것을 포기했기 때문입니다.

사실 Discount를 사용한 Control 뿐만 아니라 전체 Episodic Task와 Average Reward에서도 Policy Improvement Theorem은 통하지 않습니다. 함수 근사를 사용하는 모든 방법은 Policy Improvement Theorem을 사용할 수 없기 때문입니다. 추후 13장에서 매개변수화된 Policy를 토대로 Policy Improvement Theorem과 유사한 정리인 Policy Gradient Theorem을 대안으로 사용할 예정입니다. 하지만 Action-Value를 학습하는 방법들은 Local Improvement에 대한 보장조차 없다고 밝혀졌습니다. (Perkins and Precup, 2003) 예를 들어, $\epsilon$-greedy를 사용하는 Policy는 때때로 비효율적인 Policy를 초래할 수 있기 때문입니다. (Gordon, 1996) 이것은 현재도 이론적인 논쟁과 연구가 이루어지고 있는 부분입니다.

Differential Semi-gradient $n$-step Sarsa

Average Reward를 $n$-step Bootstrapping으로 일반화하려면 TD Error의 $n$-step 버전이 필요합니다. 함수 근사를 사용하여 식 (7.4)의 $n$-step Return을 Differential 형태로 일반화하면 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} - \bar{R}_{t+n-1} + \cdots + R_{t+n} - \bar{R}_{t+n-1} + \hat{q}(S_{t+n}, A_{t+n}, \mathbf{w}_{t+n-1}) \tag{10.14}\]

$\bar{R}$은 $r(\pi)$의 추정값이고, $n \ge 1$, $t + n < T$입니다. 만약 $t + n \ge T$라면 $G_{t:t+n} \doteq G_t$ 입니다. $n$-step TD Error는 다음과 같습니다.

\[\delta_t \doteq G_{t:t+n} - \hat{q}(S_t, A_t, \mathbf{w}) \tag{10.15}\]

Update는 Semi-gradient Sarsa의 식 (10.12)를 그대로 사용합니다. Differential Semi-Gradient $n$-step Sarsa의 완전한 Pseudocode는 다음과 같습니다.

Summary

이번 장에서는 지난 장에서 소개한 Parameterized Function Approximation 및 Semi-gradient Descent의 개념을 On-policy Control로 확장했습니다. Episodic Task에서는 확장하는 것이 크게 어렵지 않았으나, Continuing Task에서는 Average Reward라는 새로운 개념을 도입했습니다. 왜냐하면 Discount를 사용한 식은 Function Approximation을 사용할 경우 Control에 있어 여러 이론적 문제가 발생했기 때문입니다. 따라서 Average Reward $r(\pi)$를 사용하여 Differential Value Function과 Differential TD-Error를 새롭게 정의하였습니다.

다음 장에서는 Function Approximation을 사용한 Off-policy의 Control 방법에 대해 다루겠습니다.

10장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!