Planning and Learning with Tabular Methods
지금까지 배운 강화학습 방법에서 Dynamic Programming, Heuristic Search와 같이 Model이 필요한 방법을 Model-based라고 하고, Monte Carlo Method, Temporal Difference Learning과 같이 Model 없이 사용할 수 있는 방법을 Model-free라고 합니다. 해법을 구할 때 Model-based 방법은 Planning을 사용하지만 Model-free 방법은 Learning을 사용하는 차이점이 있습니다. 그러나 두 방법은 Value Function을 계산하는 과정에서 유사점이 있습니다. 두 방법 모두 미래에 발생하는 이벤트를 토대로 Value Function을 추정하기 때문입니다. 이번 장에서는 Model-based와 Model-free를 통합한 새로운 방법을 제안합니다. 지난 장에서 Monte Carlo Method과 TD(0)를 $n$-step TD로 통합하는 방법을 보여드렸는데, 이번 장의 통합 과정도 이와 유사합니다. 특히 서로 다른 두 방법이 어디까지 통합될 수 있는지에 집중할 예정입니다.
Models and Planning
Environment Model은 Agent의 Action에 Environment가 어떻게 반응할지 예측하는 데 사용할 수 있는 모든 것을 의미합니다. State와 Action이 주어졌을 때, Model은 다음 State와 받게 되는 Reward를 예측합니다. Model이 Stochastic이라면 다음 State와 받게 되는 Reward는 여러 종류가 있어서 확률에 따라 다음 State와 받게 되는 Reward가 정해집니다. 이것을 Distribution Model이라고 부릅니다. 또 다른 Model로 확률에 따라 단 하나의 Sample만 생성하는 Sample Model도 있습니다.
예를 들어, 12개의 주사위를 던져 그 합을 Modeling한다고 가정해봅시다. Distribution Model은 발생할 수 있는 모든 합을 구한 다음, 각 합계가 발생할 확률을 계산합니다. 반면에 Sample Model은 이 Probability Distribution에 따라 생성된 Sample을 다수 생성하여 확률을 계산하는 것입니다. Distribution Model을 토대로 Sample을 생성할 수도 있기 때문에 더 우수한 방법이지만, 실제 문제에서는 Distribution Model을 생성하는 것이 쉽지 않기 때문에 얻기 쉬운 Sample Model을 더 많이 사용합니다. 예를 든 12개의 주사위 합을 Modeling하는 것만 쳐도, 모든 경우의 수와 확률을 구하는 것은 쉽지 않습니다. 오히려 12개의 주사위를 굴리는 시뮬레이션 프로그램을 작성하는게 훨씬 쉽습니다. 물론 Sample Model을 토대로 가능한 합계와 그 확률을 추산하는 것은 오류가 발생하기 쉽다는 단점도 있습니다.
Model을 구했다면 그 Model을 사용하여 시뮬레이션을 할 수도 있습니다. 초기 State와 Action이 주어지면 Sample Model은 가능한 다음 State 및 Reward 등을 생성하고, Distribution Model은 발생할 확률에 따라 Weight를 부여한 모든 가능한 State와 Reward를 생성합니다. 따라서 시작점만 주어진다면 Model을 통해 Episode 전체를 생성할 수 있습니다. 이것을 Simulated Experience라고 합니다. 이렇게 Model을 기반으로 Modeling된 Environment와 상호작용하기 위한 Policy를 생성 및 개선하는 모든 프로세스를 Planning이라고 합니다.

인공지능에서 Planning은 두 가지 접근 방식으로 나뉘어 있습니다. 이 책에서 다루는 접근 방식은 State Space Planning이라고 하는데, Optimal Policy을 만드는 최적의 경로를 위한 State Space를 탐색하는 방법입니다. 이 때 Action은 State에서 다른 State로 전환하는 데 사용되며, Value Function은 State에 의해 계산됩니다. 또 다른 방법으로 Plan Space Planning이 있는데, 이것은 이름처럼 Plan Space를 탐색하는 방법입니다. Operators를 사용하여 Plan을 다른 Plan으로 전환하고, Value Function은 Plan Space에 기반하여 정의됩니다. Plan Space Planning은 강화학습 문제의 초점인 Stochastic Sequential Decision Problem에 적용하기 어렵기 때문에 여기서는 더이상 언급하지 않습니다. (참고 : Russell and Norvig, 2010)
이번 장에서 사용하는 기본 아이디어로 (1) 모든 State Space Planning은 Policy를 개선하기 위해 Value Function 계산을 중간 단계에 포함하고, (2) Simulated Experience이나 백업 연산으로 Value Function을 계산합니다. 이 구조를 Diagram으로 표현하면 다음과 같습니다.

이 방법에 가장 적합한 것은 Dynamic Programming입니다. State Space를 Sweep한 다음 각 State에 대해 가능한 Transition Distribution을 생성하고, 각 Distribution이 백업된 값을 계산한 다음 State의 추정 Value를 Update하면 됩니다. 물론 Dynamic Programming 외에 다른 State Space Planning 방법을 못쓰는 것은 아닙니다. 다른 방법 또한 이번 장에서 살펴볼 예정입니다.
Planning과 Learning의 핵심은 Backup Update를 통한 Value Function의 추정입니다. 두 방법의 차이점으로 Planning은 Model에서 생성된 Simulated Experience를 사용하는 반면, Learning은 Environment에서 생성된 Real Experience를 사용합니다. 이 차이로 인해 Experience가 얼마나 유연하게 생성될 수 있는지, 성능이 어떻게 평가되는지와 같은 또 다른 차이점을 만들어내긴 하지만, Value Function을 추정한다는 공통된 부분을 통해 많은 아이디어와 알고리즘이 두 방법에 동일하게 쓰일 수 있습니다. 특히, 다수의 Learning 알고리즘은 Planning에도 유용하게 사용할 수 있습니다. 예를 들어, 다음 알고리즘은 1-step Tabular Q-learning 알고리즘을 Planning에 도입한 예시입니다.

이번 장의 두 번째 주제는 작고 점진적인 단계로 Planning하는 것의 이점입니다. 이를 통해 계산 낭비가 거의 없이 언제든지 Planning을 중단하거나 리디렉션 할 수 있으며, 이는 Planning과 Learning을 효율적으로 융합하기 위한 핵심 요구 사항입니다. 주어진 문제가 너무 방대하여 정확하게 풀 수 없는 경우, 작은 단계로 나누어 Planning하는 것이 효율적인 접근 방식이 될 수 있습니다.
Dyna: Integrated Planning, Acting, and Learning
Planning이 일어나는 동안, Planning Agent가 Environment와 상호작용하는 동안 얻게 되는 새로운 정보는 Model을 변경할 수 있습니다. 만약 의사 결정과 Model 학습이 모두 상당한 계산량이 필요하다면, 사용 가능한 계산 자원을 적절히 배분할 필요가 있습니다. 이 문제를 해결하기 위해 이번 Section에서는 주요 기능을 통합하는 간단한 구조인 Dyna-Q를 제안합니다.
Planning Agent가 Real Experience를 하기 위해서는 최소한 다음 두 가지 조건이 필요합니다. 첫째로 Real Environment와 더 정확하게 일치하도록 Model을 개선하는 데 사용할 수 있어야 하고(Model Learning), 둘째로 이전 장들에서 논의한 강화학습 방법을 사용하여 Value Function과 Policy를 개선하는데 사용할 수 있어야 합니다(Direct Reinforcement Learning). 이들간의 관계는 아래 Diagram을 참고해주시기 바랍니다. 각 화살표는 누구에게 영향을 끼치는지 나타냅니다. Experience가 어떻게 Model을 통해 Value Function과 Policy를 개선할 수 있는지 확인하시기 바랍니다. Model을 학습하고, Model을 Planning 함으로써 Value Function과 Policy를 개선하는 것을 Indirect Reinforcement Learning이라고 합니다.
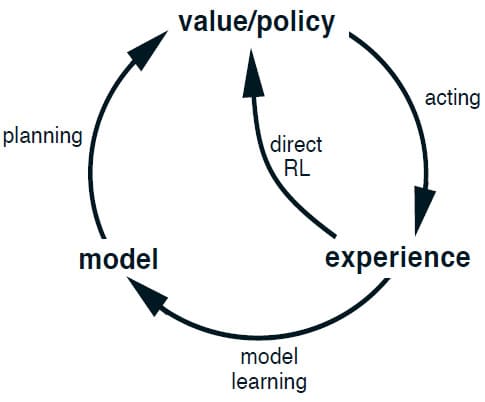
Direct RL과 Indirect RL 모두 각자의 장단점이 있습니다. Indirect RL은 제한된 양의 Experience을 최대한 활용하기 때문에 Environment와의 상호작용이 적더라도 더 나은 Policy를 유도할 수 있습니다. 반면 Direct RL은 간단하고, Model을 설계할 때 발생하는 Bias에 영향을 받지 않습니다.

Dyna-Q에는 이 Diagram에 표시된 모든 프로세스가 포함되어 있습니다. 위의 그림을 통해 그 구조를 확인할 수 있습니다. 중앙의 Real Experience를 기준으로 왼쪽을 보시면, Real Experience를 토대로 Direct RL을 수행하고 오른쪽을 보시면 Real Experience를 토대로 Model을 학습한 다음, Simulated Experience를 토대로 Planning을 수행하는 것을 볼 수 있습니다. 여기에서 사용하는 Direct RL/Planning은 일반적으로 같은 강화학습 방법을 사용하기 때문에 Final Common Path라고 부릅니다.
원칙적으로 Dyna에서 Planning, Acting, Model-Learning, 그리고 Direct RL은 동시에 병렬적으로 수행됩니다. 하지만 실제로 구현하는 컴퓨터는 직렬로 구현되어 있기 때문에, 각각의 시간 단계에서 발생하는 순서를 지정해야 합니다. Dyna-Q에서 Acting, Model-Learning, Direct RL에는 계산이 거의 필요하지 않고, 약간의 시간만 소요된다고 가정합니다. 남은 계산 자원과 시간은 모두 Planning에 할당합니다. 전체 Tabular Dyna-Q의 Pseudocode는 아래와 같습니다. 이 알고리즘에서 $Model(s, a)$는 주어진 State-Action 쌍 $(s, a)$에 대해 Model이 예상한 다음 State 및 Reward를 나타냅니다. Direct RL은 (d), Model-Learning은 (e), 그리고 Planning은 (f) 단계에서 구현되어 있습니다. 어렵게 생각하실 필요 없이 (e)와 (f)를 생략하면 그냥 1-step Q-learning과 동일한 알고리즘입니다.

Example 8.1) Dyna Maze
이번에는 간단한 예제를 통해 Dyna를 더 자세히 살펴보겠습니다. 아래 그림의 오른쪽 위를 보시면 간단한 GridWorld가 있습니다. State는 각각의 칸, Action은 동서남북 4방향으로 주어져 있습니다. 만약 갈 수 없는 방향인 경우 Agent의 State는 바뀌지 않습니다. Reward는 Goal에 도착하면 +1, 그 외에는 모두 0으로 주어집니다. Goal에 도착하면 Episode가 종료되고 다시 Start 지점으로 돌아가 새 Episode를 시작합니다. Discount는 $\gamma = 0.95$로 주어져 있습니다.

이 문제에서 초기의 Action-Value는 모두 0, Step-size Parameter $\alpha = 0.1$, Exploration Parameter $\epsilon = 0.1$으로 설정되어 있습니다. 위의 그래프는 이 문제에 대한 평균 학습 곡선을 나타내고 있습니다. Planning이 하나도 없는 Direct RL은 처음에 아무런 정보가 없기 때문에 굉장히 많은 Step을 거치고 나서야 Goal에 도달한 것을 알 수 있습니다. Step 수가 너무 커서 그래프에 표시되지 않았으나, 약 1700 Step이 소요되었습니다. 그 이후로 빠르게 Step 수가 줄어들긴 합니다만, 수렴하기까지 약 25개의 Episode가 필요함을 알 수 있습니다. 그러나 5개의 Planning만 추가해도 수렴 속도가 눈에 띄게 빨라지며, 50개의 Planning이 추가되었을 때는 3개의 Episode만에 수렴함을 알 수 있습니다.
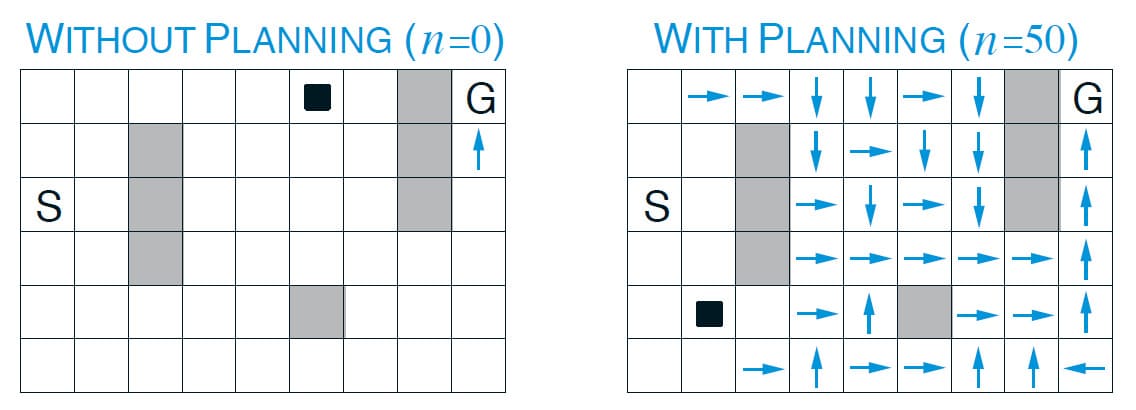
어째서 Planning을 추가했을 때 학습이 빠르게 수렴하는지는 위의 그림을 보면 알 수 있습니다. 6장에서 배운대로 1-step Q-learning은 Episode의 마지막 부분에서만 Q 값이 Update되기 때문에 수렴하기까지 속도가 오래 걸립니다. 그러나 Planning을 사용하면 Planning Step이 클 수록 하나의 Episode에서 많은 Q 값이 동시에 학습되기 때문에 그만큼 수렴이 빨라집니다.
□
When the Model Is Wrong
Example 8.1에서 보여드린 Dyna Maze 예제에서와 같이 Model의 Update는 매우 수월했습니다. 즉, Model에 대한 사전 정보 없이, 이상적으로 정확한 Model이 생성되었습니다. 그러나 이렇게 항상 우리가 원하는 대로 Model이 생성될 수는 없습니다. Model이 불완전할 수 있을 뿐만 아니라 정확하지 않을 수도 있습니다. 이렇게 되는 원인은 Environment가 Stochastic으로 주어진 경우라던가, 제한된 적은 수의 Sample만 관찰된다던가, 불완전한 근사 함수를 토대로 학습된다던가, 아니면 심지어 Environment가 바뀌었는데 그것을 관찰하지 못한 경우가 있을 수도 있습니다. 만약 Model에 이렇게 문제가 생긴다면, Planning 단계에서 Suboptimal Policy를 계산할 수 있습니다. 어떤 경우에는 Planning에 의해 계산된 Suboptimal Policy로 Model에 대한 오류를 빠르게 발견하고 수정할 수 있습니다. 다음 예제를 통해 이것이 어떤 의미인지 알아보겠습니다.
Example 8.2) Blocking Maze
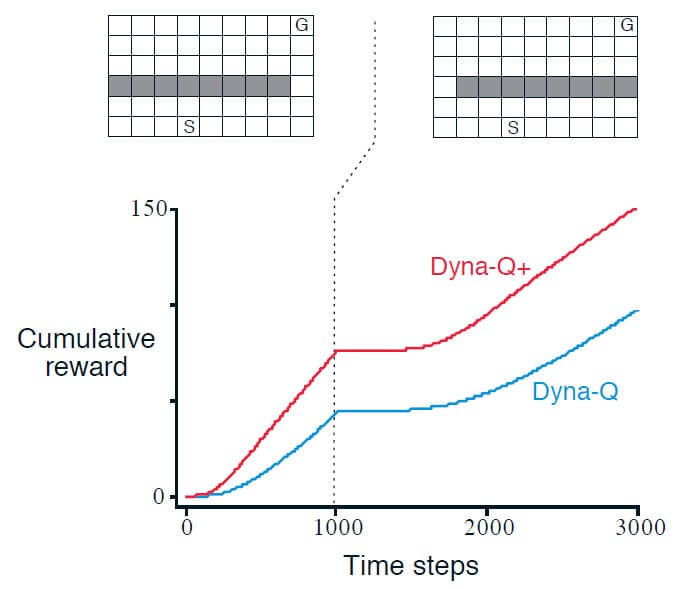
이번 예제는 비교적 사소한 Modeling 오류를 복구하는 문제입니다. 위의 그림 중 왼쪽 상단의 미로는 시작 지점 S부터 목표 지점 G 사이에 긴 벽이 존재합니다. 1000개의 시간 단계가 지나면 오른쪽과 같이 벽의 위치를 바꿉니다. 그래프는 이 문제에서 Dyna-Q와 이를 수정한 Dyna-Q+에 대한 평균 누적 Reward를 나타냅니다. 1000 시간 단계 후에 평평한 부분은 Agent가 벽 아래에서 어느 방향으로 가야 목표 지점에 도달할지 찾는 시간입니다. 이 구간이 지나면 다시 두 Agent는 목표 지점으로 갈 수 있는 최단 경로를 찾아 다시 Reward를 얻게 됩니다.
□
이렇게 Environment가 급격하게 변해 기존의 Policy를 사용하지 못하는 경우에는 누적 Reward의 차이만 있을 뿐 두 방법 모두 새로운 Policy를 찾을 수 있습니다. 문제는 Environment에서 기존의 답보다 더 좋은 새로운 답이 생기는 경우에 발생합니다. 그 예시를 다음 예제에서 보여드리겠습니다.
Example 8.3) Shortcut Maze
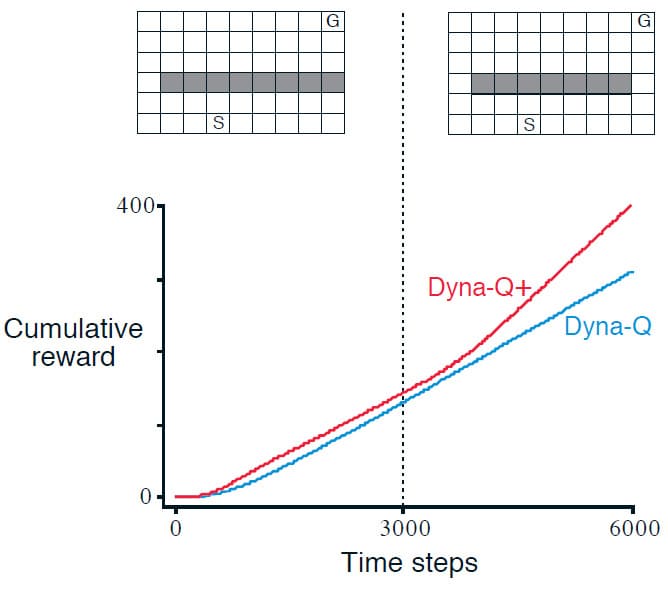
이번 예제는 왼쪽에 출구가 있고, 시작 지점 S부터 목표 지점 G 사이에 긴 벽이 있는 상황입니다. 3000 시간 단계 후에, 이번에는 오른쪽에 새로운 출구가 생깁니다. 당연히 눈으로 보았을 때는 오른쪽 출구를 통해 목표 지점 G에 가는 것이 더 빠른 경로입니다. 그러나 아래의 그래프를 보시면 Dyna-Q 알고리즘은 오른쪽에 새로운 출구를 발견하지 못해 계속 기존의 Policy를 고수하는 것을 알 수 있습니다. Dyna-Q+ 알고리즘은 이와 다르게 결국 새로운 출구를 찾기는 하나 상당 수의 시간 단계가 소요되는 것을 알 수 있습니다.
□
여기서 발생할 수 있는 또 다른 문제는 Exploration과 Exploitation 간의 조율입니다. Planning에서 Exploration은 Model을 개선하는 시도를 의미하지만, Exploitation은 현재 Model에서 주어진 최적의 방식으로 행동하는 것을 의미합니다. 강화학습에서의 Exploration vs Exploitation과 마찬가지로 완벽하게 조율할 수 있는 해법은 없지만, 간단한 Heuristic 방법으로 어느 정도 해결할 수 있습니다.
이전 예제에 언급된 Dyna-Q+가 바로 이러한 Heuristic 방법을 사용합니다. Dyna-Q+의 Agent는 Environment와의 실제 상호작용에서 State-Action 쌍이 마지막으로 선택된 이후 경과된 시간 단계를 측정합니다. 선택된 지 오래 지날수록 Model이 정확해지지 않을 가능성이 크기 때문에, 해당 State-Action 쌍을 선택하도록 유도하기 위해 보너스 Reward를 제공합니다. 예를 들어, 어떤 특정한 State-Action 쌍이 $r$의 Reward를 제공한다고 가정했을 때, 이 State-Action 쌍이 시간 단계 $\tau$ 만큼 선택되지 않는다면, 해당 State-Action 쌍의 Reward는 $r + \kappa \sqrt{\tau}$가 되는 구조입니다. 물론 이렇게 Exploration을 강제로 유도하는 것은 그만큼의 손해가 발생하나, 이전 예제와 같이 Environment가 변하는 경우에는 감수할만한 가치가 충분히 있습니다.
Prioritized Sweeping
Dyna의 Agent에서 Simulated Transition은 이전에 경험했던 모든 State-Action 쌍에서 무작위로 균일하게 선택되어 시작됩니다. 그러나 균일한 선택이 반드시 최선은 아닙니다. 상황에 따라 특정 State-Action 쌍에 초점을 맞추는 것이 Planning에 더 효율적일 수 있습니다. 예를 들어, Example 8.1에서 WITHOUT PLANNING을 보시면 첫 번째 Episode에서의 학습은 Goal 지점 직전에서만 이루어졌습니다. 두 번째 Episode가 시작할 때, Goal 지점의 직전 State-Action을 제외하고는 여전히 초기화된 0의 값만 가지고 있습니다. 즉, 이런 상황에서 대부분의 State-Action 쌍은 방문해봤자 값이 변하지 않기 때문에 Update를 하는 의미가 없습니다. 그렇기 때문에 초기 몇 번의 Episode에서의 Update는 낭비나 다를 바 없습니다.
이러한 Update 낭비를 해결하는 방법으로, 역방향 학습을 떠올려볼 수 있습니다. Goal 지점 직전 부분에서 값이 변했다면, 그 부분부터 역으로 진행하는 방법으로 낭비 없는 Update를 할 수 있기 때문입니다. 이것을 Planning에 도입한 것을 Backward Focusing이라고 합니다.
Backward Focusing을 사용해 낭비없이 많은 State-Action 쌍을 Update할 수 있지만, 모든 State-Action 쌍에 대해 유용하지 않을 수 있습니다. 어떤 State-Action 쌍의 값은 많이 Update 될 수도 있지만, 그렇지 않은 State-Action 쌍 또한 분명히 존재할 수 있기 때문입니다. 특히 Stochastic Environment에서 이럴 가능성이 높습니다. 따라서 이 때는 각 State-Action 쌍마다 우선순위를 정하여 우선순위가 높은 State-Action 쌍을 많이 방문하게 만드는 것이 좋습니다. 이렇게 우선순위에 따라 Update 하는 것을 Prioritized Sweeping이라고 합니다. 이 때, Update로 변경된 값이 클수록 우선순위가 높습니다. Update를 한 후, 값의 변화가 크다면 그만큼 적게 방문했다는 뜻이기 때문입니다. 이러한 방식으로 Update를 하게 되면 수렴할 때까지 효율적으로 전파가 가능해집니다. Deterministic Environment에서 Prioritized Sweeping에 대한 전체 Pseudocode는 다음과 같습니다.

Example 8.4) Prioritized Sweeping on Mazes

다시 미로 예제로 돌아가봅시다. 위의 그래프를 보시면 미로 문제에서 Prioritized Sweeping은 Dyna-Q 방법보다 수렴속도가 5~10배 정도 빨라짐을 알 수 있습니다. 두 방법 모두 Planning 단계를 $n=5$로 동일하게 설정한 결과입니다. (Peng and Williams (1993))
□
Stochastic Environment에 Prioritized Sweeping을 적용하는 것도 간단합니다. 각 State-Action 쌍을 경험한 횟수와 그로부터 이어지는 다음 State가 무엇이었는지를 직접 세면 됩니다. 즉, 가능한 모든 다음 State와 발생 확률을 고려하여 우선순위를 정하는 것입니다.
지금까지 Prioritized Sweeping의 장점을 위주로 소개하였으나, Prioritized Sweeping는 Planning을 효율적으로 개선하는 방법 중 하나일 뿐 최선의 방법은 아닙니다. Prioritized Sweeping의 대표적인 한계는 Expected Update를 사용한다는 것입니다. 이것은 Stochastic Environment에서 확률이 낮은 Transition에 대해 많은 계산을 낭비할 수 있습니다. 이에 반해 Sample Update는 Sampling으로 인한 분산을 감안하더라도 더 적은 계산으로 Value Function을 실제와 가깝게 추정할 수 있습니다. Expected Update와 Sample Update의 비교는 다음 Section에서 자세히 다루겠습니다.
Expected vs. Sample Updates
지금까지 배운 내용의 대부분은 Value Function을 추정하기 위한 Update 방법이었습니다. 1-step Update로 한정해서 생각해보면 크게 3가지의 요소를 토대로 분류할 수 있습니다. 첫 번째 요소는 State의 Value를 Update하는지, 아니면 Action의 Value를 Update하는지에 대한 여부입니다. 두 번째 요소는 Optimal Policy에 대한 Value를 추정하는지, 아니면 주어진 임의의 Policy에 대한 Value를 추정하는지에 대한 여부입니다. 이 두 요소를 조합했을 때 4가지 종류의 Value Function $q_{*}$, $v_{*}$, $q_{\pi}$ 그리고 $v_{\pi}$로 간단하게 표기할 수 있습니다. 마지막 세 번째 요소는 발생할 수 있는 모든 가능한 이벤트를 고려하는 Expected Update인지, 아니면 발생할 수 있는 단일 Sample을 고려한 Sample Update인지에 대한 여부입니다. 이 3가지 요소를 조합하면 총 8가지의 경우의 수가 나오며, 그 중 7개는 아래 그림처럼 정리할 수 있습니다. 한 가지가 빠진 이유는 그다지 유용한 방법이 아니기 때문입니다.

위의 그림과 같은 7가지 분류는 Learning 뿐만 아니라 Planning에도 적용할 수 있습니다. 예를 들어, 이전 Section에서 다루었던 Dyna-Q는 $q_{*}$ + Sample Update를 사용하지만, $q_{*}$ + Expected Update, 또는 $q_{\pi}$ + Sample Update를 사용할 수도 있습니다.
6장에서 1-step Sample Update를 소개할 때, Expected Update의 대안으로 소개하였습니다. 정확한 Model이 없으면 Expected Update가 불가능하기 때문에, Environment나 Sample Model의 정보를 사용하여 Sample Update를 수행할 수 있기 때문입니다. 이런 관점으로 볼 때, 만약 Sample Update와 Expected Update를 모두 사용할 수 있는 문제라면 Expected Update가 더 낫다는 것을 알 수 있습니다. Expected Update는 Sampling Error로 인한 문제가 발생하지 않기 때문에 확실히 더 낫다고 볼 수 있지만, 더 많은 계산이 필요합니다. 대부분의 문제에서 사용할 수 있는 계산 자원은 한계가 있기 때문에 두 방법을 적절하게 평가하기 위해서는 이 점을 반영해야 합니다.
구체적으로, $q_{*}$를 추정할 때 Expected Update와 Sample Update를 각각 고려해보겠습니다. State와 Action은 이산적, Approximate Value Function은 Tabular-Q, 그리고 Transition Function은 $\hat{p}(s’, r \mid s, a)$라고 가정하겠습니다. 이 때, Expected Update는 다음과 같이 표현할 수 있습니다.
\[Q(s, a) \gets \sum_{s', r} \hat{p}(s', r | s, a) \left[ r + \gamma \max_{a'} Q(s', a') \right] \tag{8.1}\]Sample Update 버전은 아래와 같이 Q-learning과 유사한 형태로 표현됩니다. $\alpha$는 step-size parameter입니다.
\[Q(s, a) \gets Q(s, a) + \alpha \left[ R + \gamma \max_{a'} Q(S', a') - Q(s, a) \right] \tag{8.2}\]Expected Update와 Sample Update의 차이는 State와 Action을 토대로 가능한 다음 State가 여러 개가 존재할 수 있는 Stochastic Environment에서 발생합니다. 만약 Deterministic Environment이라면, $\alpha = 1$로 설정했을 때 Expected Update와 Sample Update는 동일합니다. Stochastic Environment에서 Sample Update는 Sampling Error의 영향을 받지만, 한번에 하나의 다음 State만 고려하기 때문에 계산이 적고, Expected Update는 모든 가능한 다음 State를 고려하기 때문에 Sampling Error가 존재하지 않지만 그만큼 많은 계산량을 필요로 합니다. 가능한 다음 State의 개수를 Branching Factor $b$라고 하는데, Expected Update는 Sample Update보다 대략 $b$배 만큼 더 많은 계산이 필요합니다.
Expected Update를 하는데 충분한 계산 자원과 시간이 있는 경우, Expected Update는 Sampling Error가 없기 때문에 $b$번의 Sample Update보다 좋은 추정 결과를 보입니다. 그러나 많은 State-Action 쌍이 있는 큰 문제에서는 충분한 계산 자원이나 시간이 없기 때문에 Sample Update가 더 나은 추정 결과를 보이게 됩니다. 그렇다면 어떤 상황에서 Expected Update를 사용할 지, Sample Update를 사용할 지를 생각해보겠습니다.
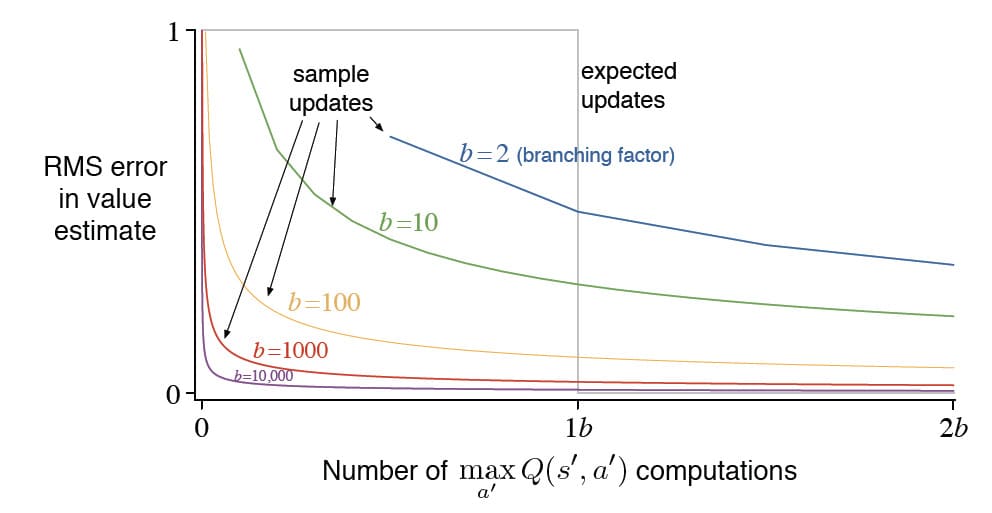
위의 그래프는 다양한 $b$의 값을 토대로 Expected Update와 Sample Update를 비교한 결과입니다. Expected Update가 $b$만큼 연산을 했다는 것은 모든 State-Action 쌍을 고려했다는 것이므로 $b$ 이후에 RMS error는 0이 됩니다. Sample Update는 대략 $\sqrt{\frac{b-1}{bt}}$ 그래프의 모양으로 RMS error가 감소합니다. $t$는 수행된 Sample Update의 수 입니다. 이 그래프로 알 수 있는 점은 적당히 큰 $b$의 경우 Sample Update의 오류가 생각보다 빨리 줄어든다는 것입니다. 이러한 결과는 Sample Update가 확률론적 분기 요인이 크고 State가 너무 많아 정확하게 풀 수 없는 문제에서는 Expected Update보다 우수할 수 있음을 시사합니다.
Trajectory Sampling
이번 Section에서는 Update를 분류하는 두 가지 방법을 비교합니다. 첫 번째는 Dynamic Programming의 고전적인 접근 방법으로 전체 State(또는 State-Action 쌍)에 대해 Sweep을 수행하고 각 State(또는 State-Action)의 Value를 Update합니다. 이 방법은 한 번의 Sweep당 한 번의 Update를 수행하는데, Sweep에 오랜 시간이 걸릴 수 있는 대규모 문제에 적합하지 않을 수 있습니다.
두 번째는 특정한 Distribution에 따라 State, 또는 State-Action을 Sampling하는 것입니다. Dyna-Q와 같이 Uniform Sampling을 할 수도 있지만, 문제에 따라서 Uniform Sampling은 적합하지 않을 수도 있습니다. Sampling을 하는 또 다른 방법으로는 On-policy Distribution에 따라 Sampling하는 것입니다. 즉, 현재의 Policy를 따를 때 관찰할 수 있는 Distribution에 따라 Sampling 및 Update를 하는 것입니다. 이 방법의 장점은 단순히 현재 Policy에 따라 Model과 상호 작용함으로써 쉽게 생성할 수 있다는 것입니다. Episodic Task나 Continuing Task 모두 상관없이 사용할 수 있으며, Model을 기반으로 시뮬레이션함으로써 Update를 수행합니다. 이 방법을 Trajectory Sampling이라고 합니다.
On-policy Distribution에 초점을 맞추면 중요하지 않은 수많은 State(또는 State-Action) 쌍이 무시되기 때문에 유리할 수도 있지만, 같은 이유로 오래 Update되지 않은 부분이 계속 영향을 끼치기 때문에 불리할 수도 있습니다. 이 책에서는 이것을 실험을 통해 경험적으로 평가하였습니다. 실험에서는 식 (8.1)과 같은 1-step Expected Tabular Update를 사용하여 Uniform Distribution과 On-policy Distribution으로 나누어 시뮬레이션했습니다. 두 방법 모두 $\epsilon = 0.1$로 설정한 $\epsilon$-greedy policy를 사용하였으며, Discount는 무시하였습니다. 모든 State에서 Branching Factor $b$는 동일하게 설정하였으며, 모든 State에서 Episode가 종료될 확률은 0.1입니다. 각 Transition에 대한 Reward는 Expectation이 0, Variance가 1인 Normal Distribution을 따르도록 설정하였습니다.
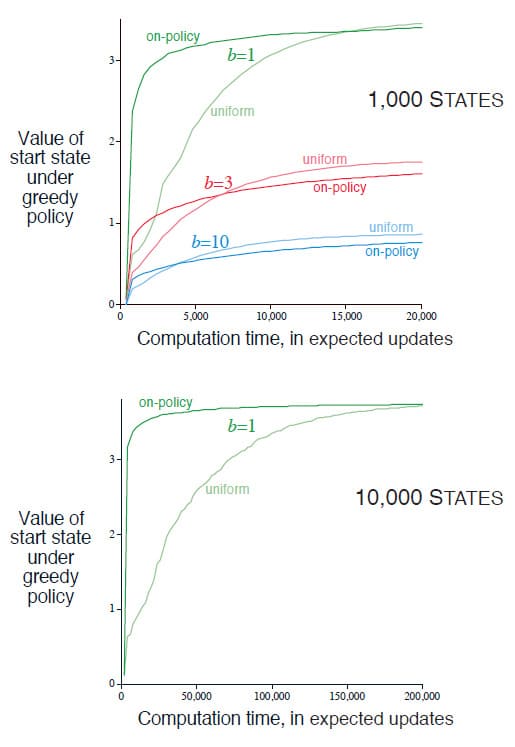
위의 그래프 중 윗부분은 1000개의 State와 Branching Factor를 각각 1, 3, 10으로 설정한 Environment에서 200개의 Sample에 대한 평균 결과를 나타냅니다. 각 Policy의 우수성은 Expected Update가 완료된 Update의 수에 대한 함수로 표현합니다. 모든 경우에서 On-policy Distribution에 따른 Sampling은 Uniform Distribution에 비해 초기에 더 빨리 좋은 성능을 보여주는 것을 알 수 있습니다. 아래쪽의 그래프는 10000개의 State에서 Branching Factor가 1인 경우에서의 실험입니다. 두 그래프를 토대로 State의 개수나 Branching Factor에 상관 없이 항상 On-policy Distribution에 따른 Sampling은 Uniform Distribution의 Sampling에 비해 초기에 우수한 성능을 보임을 알 수 있습니다.
그러나 위의 그래프를 다시보면, Branching Factor가 큰 경우에는 장기적으로 보았을 때 Uniform Distribution의 Sampling이 약간 더 우수한 성능을 보입니다. 즉, 단기적으로는 On-policy Distribution에 따른 Sampling이 빠르게 수렴값에 가까워지지만, 장기적으로는 Uniform Distribution의 Sampling이 더 우수한 성능을 보일 수도 있습니다.
Real-time Dynamic Programming
Real-time Dynamic Programming (RTDP)은 Dynamic Programming의 Value Iteration을 On-policy Trajectory Sampling으로 구현한 버전입니다. Dynamic Programming은 Sweep 기반 Policy Iteration과 밀접하게 관련되어 있기 때문에 RTDP를 통해 On-policy Trajectory Sampling이 어떤 이점이 있는지 쉽게 비교할 수 있습니다. RTDP는 식 (4.10)에 정의한 대로 Expected Tabular Value Iteration을 통해 실제, 또는 시뮬레이션 된 Trajectory에서 방문한 State의 Value를 Update합니다.
RTDP는 Section 4.5에서 언급한 Asynchronous DP의 한 종류입니다. RTDP에서 Update 순서는 실제, 또는 시뮬레이션 된 Trajectory에서 방문한 순서에 의해 결정됩니다.
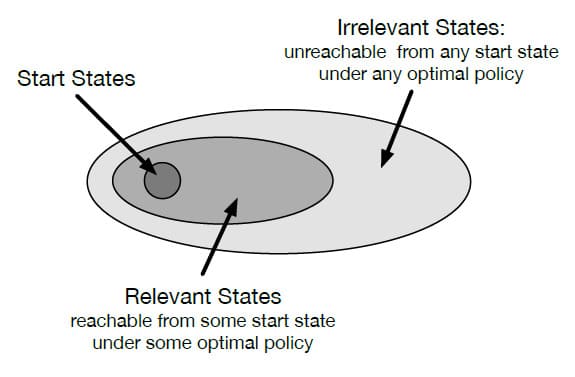
만약 Trajectory가 지정된 시작 State의 집합에서만 시작할 수 있고, 주어진 Policy에 대한 Prediction에만 관심이 있는 경우, On-policy Trajectory Sampling을 통해 주어진 Policy로 도달할 수 없는 State들은 완전히 무시할 수 있습니다. 주어진 Policy를 평가하는게 아니라 Optimal Policy를 찾는 것이 목표인 Control에서 Optimal Policy로 도달할 수 없는 State가 있는 경우 그 State로 가는 Action을 선택할 필요가 없습니다. 이렇게 Optimal Policy와 관련 없는 State에 대해 임의의 Action을 지정하거나, 정의하지 않을 수도 있는 Policy를 Optimal Partial Policy라고 합니다. 표현이 조금 헷갈리지만, 아래 그림을 보시면 무슨 뜻인지 이해하실 수 있습니다.
그러나 Sarsa와 같은 On-policy Trajectory Sampling Control에서 Optimal Partial Policy를 찾기 위해서는 일반적으로 모든 State-Action 쌍을 무한히 방문해야 합니다. 이것은 Section 5.3과 같은 Assumption of Exploring Starts를 사용할 수도 있지만, Prediction과 달리 Control에서는 Optimal Policy으로 수렴하기 위해 State, 또는 State-Action 쌍 Update를 중지할 수 없습니다.
이와 다르게 RTDP의 가장 큰 장점은 합리적인 조건을 만족하는 일부 문제에 대해 모든 State를 무한히 자주 방문하지 않거나, Optimal Policy와 관련 없는 일부 State를 전혀 방문하지 않고도 Optimal Policy를 찾는 것이 보장된다는 것입니다. 이는 State가 매우 많아 단일 Sweep도 수행하기 힘든 문제를 해결할 때 큰 장점이 될 수 있습니다.
Example 8.6) RTDP on the Racetrack
구체적인 예제를 통해 Dynamic Programming과 RTDP를 비교해보겠습니다. 아래의 그림과 같이 자동차가 Starting line에서 Finish line까지 도달하는 것이 목표인 Grid World 문제가 있습니다. Starting line에서 Finish line까지 도달하기 위해서는 자동차가 오른쪽으로 턴하는 Action이 반드시 필요한데, 트랙을 벗어나지 않으면서 가능한 빨리 Finish line에 도달해야합니다. 각 Episode는 자동차가 Finish line에 도달하면 종료됩니다.
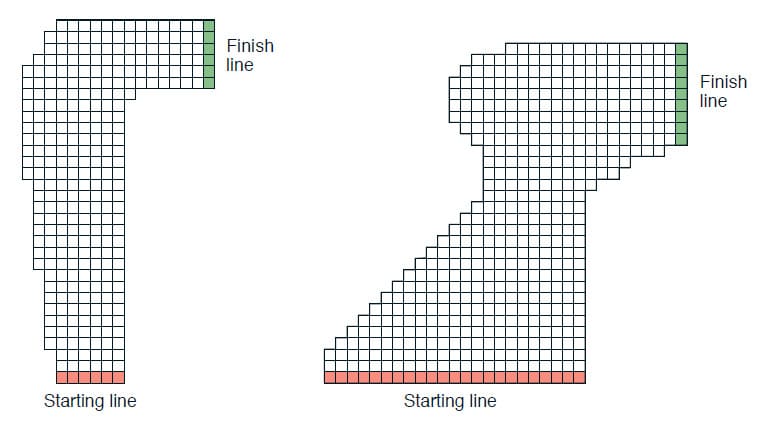
State의 집합은 자동차의 속도가 되는데, Starting line에서 속도는 0입니다. 속도의 제한은 딱히 없으므로 State의 집합은 무한대라고 볼 수 있습니다. 하지만 0부터 시작하는 속도가 갑자기 무한대에 가까워질수는 없으니, 실질적으로 도달할 수 있는 속도는 유한하다고 볼 수 있습니다. Reward는 모든 단계에서 -1이고, 만약 자동차가 트랙의 경계에 부딪히면 Starting line의 무작위 지점으로 이동하고 Episode가 계속됩니다.
예제 중 왼쪽의 그림은 시작 State에서 도달할 수 있는 State가 총 9,115개입니다. 하지만 실제로 Optimal Policy와 관련이 있는 State는 그 중 599개 뿐입니다. 이 문제를 Dynamic Programming과 RTDP로 각각 수행했을 때 평균적인 결과는 아래 표와 같습니다. 두 방법 모두 초기 값은 동일합니다.

Dynamic Programming은 각 State 집합 전체를 Sweep하는 Value Iteration이며, Sweep 한 번에 하나의 State가 Update됩니다. Dynamic Programming에서는 State를 Update했을 때 그 변동값이 $10^{-4}$ 미만일 때 수렴된 것으로 판단하였고, RTDP는 20회 이상의 Episode에서 Finish Line을 통과한 시간이 비슷한 시간 단계일 때 수렴한 것으로 판단하였습니다.
두 방법 모두 평균적으로 14~15 시간 단계를 소요하는 Optimal Policy를 생성하였지만, RTDP는 Dynamic Programming이 수행한 Update 수의 절반만 사용했습니다. 이것이 바로 On-policy Trajectory Sampling의 결과입니다. Dynamic Programming은 각각의 Sweep에서 모든 State의 Value를 Update했지만, RTDP는 Optimal Policy와 관련된 일부의 State만 Update하였습니다. RTDP는 평균적으로 100회 이하로 방문한 State의 98.45%를, 10회 이하로 방문한 State의 80.51%의 Value를 Update했습니다. 또한 약 290개의 State의 Value는 전혀 Update하지 않았습니다.
□
RTDP의 또 다른 장점은 Value Function이 Optimal Value Function $v_{*}$에 접근함에 따라 Agent가 Policy를 따라 사용하는 Trajectory가 Optimal Policy에 가까워진다는 것입니다. 이것은 Value Iteration 또한 알고리즘이 종료되기 직전의 Value Function은 $v_{*}$에 가깝고 이 때의 Greedy Policy도 Optimal Policy에 가깝지만, Value Iteration이 종료되기 전의 Greedy Policy가 Optimal Policy와 가까운지 확인하는 것은 Dynamic Programming에 포함되어 있지 않으며, 그것을 구현하기 위해서는 상당한 추가 계산이 필요합니다.
이 RTDP 예제를 통해 Trajectory Sampling의 몇 가지 장점을 알 수 있었습니다. 기존의 Value Iteration은 모든 State의 Value를 계속 Update했지만, RTDP는 목표와 관련된 State의 집합에만 초점을 맞췄습니다. 이 초점은 학습이 진행될수록 점점 더 좁아지며, 결국에는 Optimal Policy를 구성하는 State에만 초점을 맞추도록 수렴됩니다. RTDP는 Sweep 기반 Value Iteration에 비해 약 50%의 계산만 사용하고도 Control을 성공적으로 수행하였습니다.
Planning at Decision Time
지금까지 이번 장의 내용은 Model에서 얻은 Simulated Experience를 기반으로 Policy나 Value Function을 개선하기 위해 Planning을 사용했습니다. 현재 State에서 Action을 선택하기 전에, 현재 State를 포함한 이전의 많은 State에서 Action을 선택하는데 Planning을 사용했습니다. 이런 개념으로, Planning은 현재 State에만 집중되지 않습니다. 이렇게 사용되는 Planning을 Background Planning이라고 합니다.
Planning을 사용하는 또 다른 방법은 매번 새로운 State $S_t$를 방문한 후, Planning을 시작하고 완료하는 것입니다. 즉, State $S_{t+1}$을 방문한 후, Planning을 시작하여 $A_{t+1}$을 생성하는 방식입니다. 이런 사용 방법은 State의 Value만 사용할 수 있고, Model로부터 예측한 다음 State의 Value를 토대로 Action을 선택합니다. 이 방법은 Planning이 특정 State에 초점을 맞추게 됩니다. 이 방법을 Decision-time Planning이라고 합니다.
Decision-time Planning은 Value와 Policy가 현재 State와 Action의 선택에 따라 달라지므로 Planning 과정에서 생성된 Value와 Policy는 현재 State에서 Action을 선택한 후 삭제됩니다. 이것이 문제처럼 보일 수 있지만, 일반적인 Environment에서는 매우 많은 State가 있고, 한번 State를 방문한 후 오랫동안 같은 State로 돌아갈 가능성이 거의 없기 때문에 큰 문제는 아닙니다. 방문하는 State마다 Planning을 수행하기 때문에, Decision-time Planning은 빠른 응답이 필요하지 않은 Environment에서 유용합니다. 예를 들면, 체스 게임에서는 한 번의 Action에 몇 초 ~ 몇 분의 계산 시간이 허용될 수 있습니다. 다만 Routing과 같이 즉각적으로 빠른 응답이 필요한 Environment에서는 Background Planning을 사용하여 각 State에 대해 신속하게 적용할 수 있는 Policy를 계산하는 것이 더 좋습니다.
Heuristic Search
인공지능의 고전적인 State-space Planning 방법은 Heuristic Search로 알려진 Decision-time Planning 방법입니다. Heuristic Search에서는 만나는 State마다 Tree를 생성합니다. Tree의 Leaf node에 추정한 Value Function를 적용하고, 현재 State를 Root node로 두어 Leaf node부터 Root node까지 거꾸로 올라가는(Backup) 방식으로 탐색을 합니다. 이 과정은 현재 State에 대한 State-Action 쌍이 담긴 노드에서 중지되며, 계산한 Backup 값 중 현재 State에서 가장 좋은 Action을 선택한 다음 나머지 Backup 값은 폐기합니다.
기존의 Heuristic Search에서는 추정한 Value Function가 변경되었을 때 Backup된 값을 저장하지 않았습니다. 왜냐하면 기본적으로 Value Function은 사람이 설계하는 것이고, 검색을 한다고 해서 그 값이 변경되지는 않기 때문입니다. 하지만 Heuristic Search 도중에 계산된 Backup 값이나, 지금까지 배운 다른 방법들을 사용하여 Value Function을 개선해볼 수는 있습니다.
Heuristic Search를 통해 더 나은 Action을 선택하는 방법은 그만큼 더 Tree를 깊게 생성해서 검색하는 것입니다. 만약 완벽한 Model(그리고 불완전한 Value Function)이 주어진다면 깊게 검색할수록 일반적으로 더 나은 Policy를 만들 수 있습니다. 극단적으로 Episode 끝까지 탐색할 수 있다면 불완전한 Value Function일지라도 Optimal Action을 선택할 수 있습니다. 하지만 더 깊게 검색할수록 더 많은 계산이 필요하기 때문에 그만큼 응답 시간이 느려진다는 단점도 있습니다. (이것에 대한 구체적인 예시는 뒤에 나오는 Section 16.1의 TD-Gammon을 참고해주시기 바랍니다)
Heuristic Search에서 가장 중요한 것이 현재 State임을 간과해서는 안됩니다. Heuristic Search는 검색 트리가 현재 State에서 즉시 사용할 수 있는 Action이나 후속 State에 집중되어 있기 때문입니다. 가령, 계산 자원과 메모리 자원은 임박한 이벤트에 우선적으로 할당되어야 합니다.
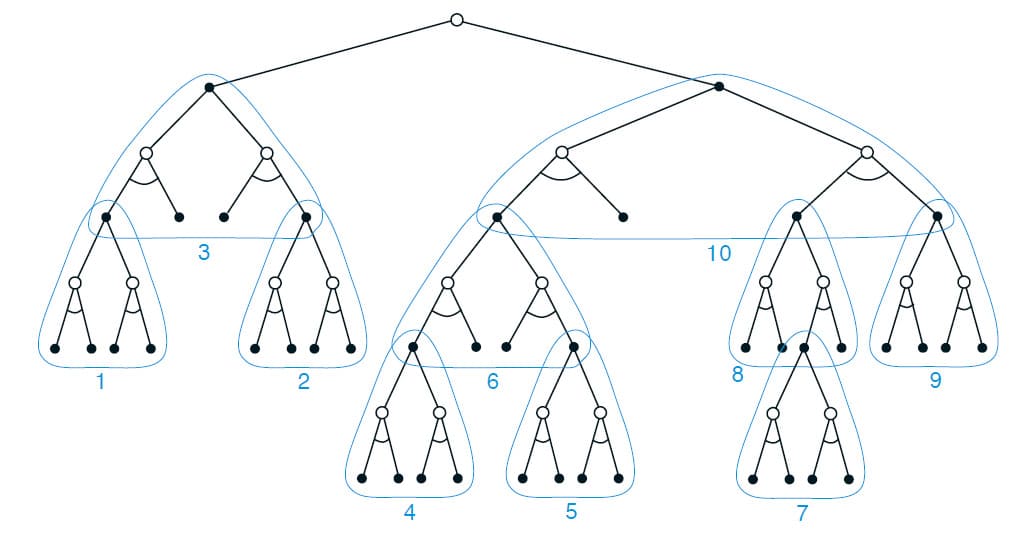
Update의 Distribution은 현재 State와 가능한 후속 State에 초점을 맞추기 위해 지금까지와 유사한 방식으로 변경할 수 있습니다. 제한적이지만 Heuristic Search를 사용하여 Search Tree를 구성한 다음, 위의 그림과 같이 상향식으로 1-step Update를 수행할 수 있습니다. Update가 이러한 방식으로 이루어지고 테이블 형식으로(Tabular) 사용된다면 Depth-first Heuristic Search와 정확히 동일한 Update라고 볼 수 있습니다. 모든 State Space 검색은 이렇게 다수의 1-step Update를 결합하는 것으로 볼 수 있습니다. 즉, 깊게 검색할수록 성능이 향상하는 이유는 multi-step을 사용하기 때문이 아니라, 현재 State로부터 바로 다음에 있는 State와 Action에 대한 Update의 집중 때문입니다. Action을 결정하는 것에 대해 많은 양의 계산을 할당함으로써 그렇지 않은 Update보다 더 나은 의사 결정을 수행할 수 있습니다.
Rollout Algorithms
Rollout Algorithm은 현재 State에서 시작하여 Simulated Trajectory에 적용된 Monte Carlo Control을 기반으로 하는 Decision-time Planning 알고리즘입니다. 현재 State에서 가능한 Action 각각에서 시작하여 주어진 Policy를 따라 Simulated Trajectory의 Reward를 평균화하여 주어진 Policy에 대한 Action Value를 추정합니다. 추정한 Action Value가 충분히 정확하다고 판단되면 가장 높은 추정값을 갖는 Action이 선택되고, 그 Action의 결과로 생성된 다음 State에서 이 과정이 반복됩니다. Rollout 이라는 이름이 붙은 이유는 주사위를 여러번 던져서 주사위의 Value를 추정하는 것에서 유래했습니다. (Tesauro and Galperin, 1997)
5장에서 설명한 Monte Carlo Control 알고리즘과 달리 Rollout Algorithm의 목표는 주어진 Policy $\pi$에 대해 Optimal Action Value Function $q_{*}$를 찾거나, Action Value Function $q_{\pi}$를 추정하는 것이 아닙니다. 그 대신 주어진 Policy에 대해 현재 State에 대한 Action Value의 Monte Carlo Prediction을 계산합니다. (이것을 Rollout Policy라고 부릅니다) Decision-time Planning 알고리즘으로써, 사용한 Action Value의 추정값은 바로 폐기합니다. Rollout Algorithm은 모든 State-Action 쌍에 대한 결과를 Sampling할 필요가 없고, State 공간이나 State-Action 공간에 대한 함수를 근사화할 필요가 없기 때문에 구현하기가 비교적 간단한 장점이 있습니다.
Rollout Algorithm의 목표는 Rollout Policy를 개선하는 것입니다. 그러나 이 과정에서 중요한 Trade-off가 있는데, Rollout Policy를 향상시킬수록 시뮬레이션하는데 더 많은 시간이 필요하다는 것입니다. Rollout Algorithm은 Decision-time Planning 방법으로써 엄격한 시간 제약을 충족해야 합니다. Rollout Algorithm에 필요한 계산 시간은 ① 각 결정에 대해 평가해야하는 Action의 수, ② 유용한 Sample Reward를 얻는 데 필요한 Simulated Trajectory의 시간 단계 수, ③ Rollout Policy가 결정을 내리는 데 걸리는 시간, 그리고 ④ 우수한 Monte Carlo Action Value 추정치를 얻기 위해 필요한 Simulated Trajectory의 수가 있습니다.
이러한 요소들의 균형을 맞추는 것은 Rollout 방법을 사용할 때 중요하지만, 이를 조금 완화할 수 있는 몇 가지 방법이 있습니다. 첫째로, Monte Carlo 시행은 서로 독립적이기 때문에 여러 개의 프로세서에서 이 시행들을 병렬적으로 실행할 수 있습니다. 둘째로, 5장에서 Episode를 부분 종료한 테크닉을 활용하는 것입니다. (Tesauro and Galperin, 1997)이 제안한 것처럼 Monte Carlo 시뮬레이션을 모니터링하여 최적이 될 것 같지 않은 Action을 미리 제거할 수도 있습니다.
Rollout Algorithm은 Value나 Policy에 대한 장기적인 기억을 유지하지 않기 때문에 일반적으로 학습 알고리즘으로 간주하지 않습니다. 그러나 Rollout Algorithm은 이 책에서 다루는 강화학습의 일부 특징을 활용합니다. Rollout Algorithm은 Sample Trajectory의 Return을 평균화하는 과정에서 Environment의 Sample Model과 상호작용합니다. 이런 식으로 전체 Sweep을 사용하지 않고 Expected Update 대신 Sample에 의존하여 Model의 필요성을 피하는 강화학습의 특성을 갖고있기 때문입니다. 마지막으로 Rollout Algorithm은 추정된 Action Value에 대해 Greedy Action을 선택함으로써 Policy Improvement 속성을 이용한다는 점이 있습니다.
Monte Carlo Tree Search
Monte Carlo Tree Search (MCTS)는 최근에 나온 Decision-time Planning의 가장 핫한 예시입니다. MCTS는 기본적으로 이전 Section에서 설명한 Rollout Algorithm에 기반하지만, 시뮬레이션에서 보다 높은 Reward를 받는 Trajectory로 연속적으로 유도하기 위해, Monte Carlo 시뮬레이션에서 얻은 Value 추정값을 누적하는 수단을 추가하였습니다. MCTS는 2016년 AlphaGo가 이세돌을 꺾는 데 결정적인 역할을 한 알고리즘입니다. 물론 MCTS는 게임에 국한된 알고리즘은 아닙니다.
MCTS가 실행되는 순서는 기존과 조금 다른데, 주어진 State에서 후속 State가 먼저 발생한 후 그 State를 만들기 위한 Action을 선택하는 방식입니다. Rollout Algorithm에서와 같이 각각의 실행은 현재 State에서 시작해서 최종 State로 실행되기까지 많은 Trajectory를 시뮬레이션하는 반복 프로세스입니다. MCTS의 핵심 아이디어는 이전 시뮬레이션에서 높은 평가를 받은 Trajectory의 초기 부분에 집중하여, 연속적인 시뮬레이션을 수행하는 것입니다. MCTS를 구현할 때, 다음 Action을 선택할 때 사용한 추정한 Value Function이나 Policy를 보존하는 경우가 많으나, 그렇게 하지 않아도 문제는 없습니다.
대부분 Simulated Trajectory의 Action들은 단순한 Policy에 의해 생성되는데, Rollout Algorithm에 사용되는 Policy이기 때문에 Rollout Policy라고 합니다. Rollout Policy와 Model 모두 많은 계산이 필요하지 않다면 짧은 시간에 많은 Simulated Trajectory를 생성할 수 있습니다. 모든 Tabular Monte Carlo Method에서 State-Action 쌍의 Value는 해당 쌍의 Simulated Reward의 평균으로 추정됩니다. Monte Carlo의 Value Prediction은 아래 그림과 같이 현재 State를 Root로 하는 Tree 구조를 가지며, 도달할 가능성이 가장 높은 State-Action 쌍의 하위 집합만 유지됩니다. MCTS는 Simulated Trajectory의 결과를 기반으로 최적의 State가 될 수 있는 후보들을 노드에 추가하여 Tree를 확장합니다. 이러한 State에 대해 Action 중 일부는 Value 추정값을 가지고 있으므로 Exploration과 Exploitation를 잘 조절하여 Tree Policy라는 Policy를 사용할 수 있습니다.
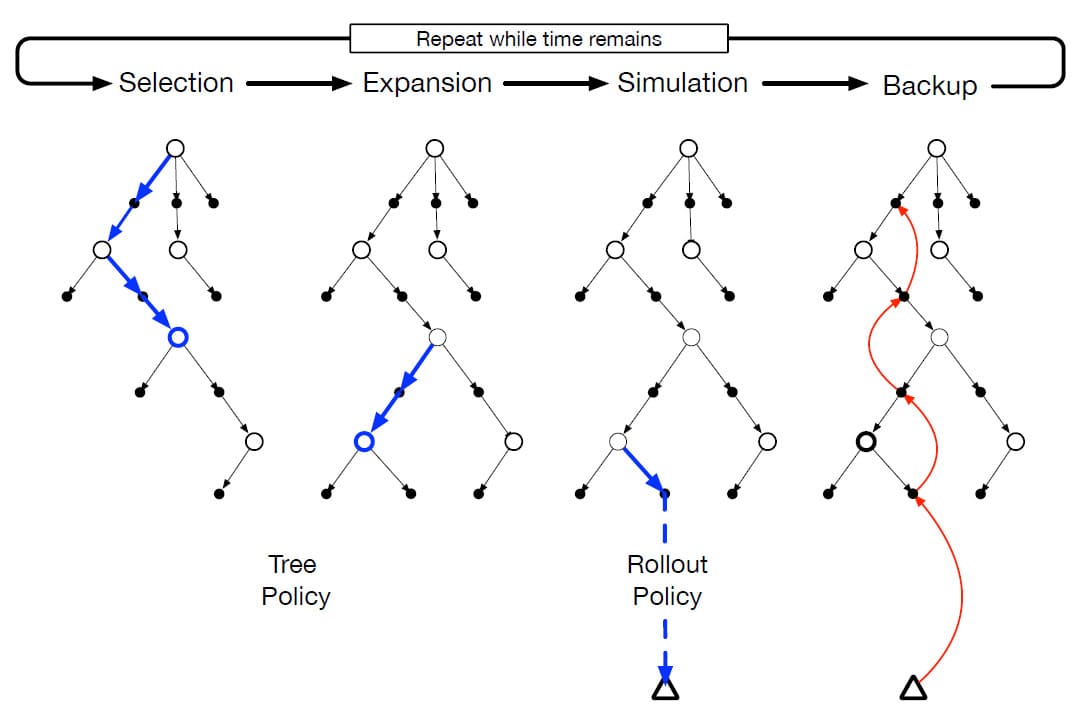
위의 그림은 MCTS의 기본 버전입니다. 각 단계에 대해 조금 더 자세히 설명하면,
- Selection : Root Node에서 시작하여 Tree의 가장자리에 연결된 Action Value를 기반으로 Tree Policy를 사용해 Tree를 순회하며 Leaf Node를 선택합니다.
- Expansion : 일부 반복 과정 중에 탐색되지 않은 Action을 선택함으로써, 선택한 노드에서 도달한 하나 이상의 자식 노드를 추가하여 Leaf Node를 확장합니다.
- Simulation : Rollout Policy를 사용하여 선택한 노드, 또는 새로 추가된 자식 노드 중 하나에서 전체 Episode를 시뮬레이션합니다. 결과는 Tree Policy에 의해 먼저 선택된 Action과 Rollout Policy에 의해 Tree 이후의 Action이 포함된 Monte Carlo 시행입니다.
- Backup : 시뮬레이션된 Episode에 의해 생성된 Return은 MCTS의 반복 과정에서 Tree Policy가 수행한 Action Value를 Update하거나, 초기화하기 위해 백업됩니다. Rollout Policy에 의해 Tree 바깥에서 방문한 State 및 Action에 대한 Value는 저장되지 않습니다.
MCTS는 시간적으로, 그리고 계산 리소스가 허용하는 만큼 이 4단계를 계속 반복합니다. 그 후 마지막으로 이 반복 과정을 통해 누적된 통계에 의해 Root Node의 Action이 선택됩니다. 이 때 Action을 선택하는 기준은 여러 가지가 있는데, 예를 들어 Root Node에서 선택할 수 있는 모든 Action 중 가장 Value가 큰 Action을 선택할 수도 있고, 또는 가장 안좋은 후속 State를 피할 수 있는 Action을 선택할 수도 있습니다. 어쨌든 이렇게 Action을 선택해서 다음 State에 도달하면, MCTS를 다시 실행하여 다음 Action을 선택합니다. 이 때, 다음 State에 도달하고 나면 이전에 계산했던 Tree는 모두 폐기됩니다.
MCTS가 어떻게 이렇게 우수한 결과를 도출할 수 있는지는 이 책에서 설명하는 강화학습의 원리와 연관시키면 이해할 수 있습니다. 기본적으로 MCTS는 Root Node에서 시작하는 시뮬레이션이 적용된 Monte Carlo Control을 기반으로 하는 Decision-time Planning 알고리즘입니다. 즉, 이전 Section에서 설명한 Rollout Algorithm의 한 종류입니다. 따라서 Online, Incremental, Sample 기반의 Value Prediction 및 Policy Improvement의 장점을 그대로 보유하고 있습니다. 이 외에도 Tree에 Action-Value 추정값을 저장하고, 강화학습의 Sample Update를 사용하여 Update합니다. 이것은 Monte Carlo 시행을 할 때, 초기에 높은 Reward를 갖는 Trajectory를 따르는 경로에 집중하는 효과가 있습니다. 또한 Tree를 점진적으로 확장함으로써 이러한 Trajectory에서 방문한 State-Action 쌍의 추정값을 효과적으로 저장 및 조회할 수 있습니다. 따라서 MCTS는 탐색에 과거 경험을 사용하는 이점을 가지면서 Action-Value Function을 전체적으로 근사해야하는 문제를 피할 수 있습니다.
MCTS의 이러한 성공은 강화학습 뿐만 아니라 인공지능 전반에 큰 영향을 끼쳤으며, 현재에도 여러 응용 프로그램에 사용하기 위해 수정 및 확장을 연구하고 있습니다.
Summary of the Chapter
Planning에는 Environment Model이 필요합니다. Distribution Model은 다음 State의 확률과 가능한 Action에 대한 Reward로 구성됩니다. Sample Model은 이러한 확률에 따라 생성된 단일 Transition 및 Reward를 생성합니다. Dynamic Programming은 가능한 모든 다음 State 및 Reward에 대한 기대값을 계산하는 Expected Update를 사용하기 때문에 Distribution Model이 필요합니다. 반면에 대부분의 강화학습 알고리즘에서는 Sample Update를 사용하므로 Sample Model을 사용합니다. Sample Model은 일반적으로 Distribution Model보다 훨씬 쉽게 얻을 수 있습니다.
이 장에서는 최적의 Action을 Learning하는 것과 Planning하는 것 사이에 관계를 강조하였습니다. 두 방법 모두 동일하게 Value Function을 추정하고, 작은 Backup 계산을 점진적으로 Update합니다. 이 공통점을 사용해 Learning과 Planning 모두 동일한 Value Function Prediction을 Update하도록 설계함으로써 간단하게 통합할 수 있습니다. 또한 어떤 Learning 방법이라도 Real Experience가 아니라 Model에 의한 Simulated Experience에 적용하기만 하면 Planning에 사용할 수 있습니다.
Incremental Planning 방법을 Acting 및 Model Learning과 통합하는 것은 간단합니다. Planning, Acting, Model Learning 간에는 순환적으로 상호작용하며, 이를 통합하는 가장 간단한 방식은 모든 프로세스를 비동기화하여 병렬식으로 수행하는 것입니다. 이 방법은 프로세스 간의 계산 자원을 효율적으로 분배할 수 있다는 장점이 있습니다.
또한 이 장에서 State Space에서 Planning 방법에 대해 다루었습니다. 첫째로 Update 크기의 변화입니다. Update가 작을수록 Planning이 더 Incremental 될 수 있습니다. 가장 작은 Update는 Dyna와 같은 1-step Sample Update입니다. 둘째로 Update의 Distribution, 즉 검색의 초점입니다. Prioritized Sweeping은 최근에 값이 변경된 State의 역방향에 초점을 맞춥니다. On-policy Trajectory Sampling은 Agent가 Environment를 제어할 때 만날 수 있는 State, 또는 State-Action 쌍에 초점을 둡니다. 이를 통해 Prediction이나 Control과 관련이 없는 State Space의 일부를 건너뛸 수 있습니다. Real-time Dynamic Programming은 Value Iteration의 On-policy Trajectory Sampling 버전으로써 기존 Sweep 기반의 Policy Iteration에 비해 몇 가지 장점을 보여줍니다.
Planning은 Agent가 Environment와 상호작용할 때 실제로 발생하는 State에도 초점을 맞출 수도 있습니다. 이것의 가장 중요한 형태는 Planning이 Action을 선택하는 프로세스의 일부로 수행될 때입니다. 인공지능 분야에서 연구되는 고전적인 Heuristic Search가 그 예시입니다. 그 외에 Online, Incremental, Sample에 기반한 Value Prediction 및 Policy Improvement의 이점을 제공하는 Rollout Algorithm과 Monte Carlo Tree Search가 있습니다.
Summary of Part I : Dimensions
8장을 마지막으로 이 책의 1부가 끝납니다. 1부에서는 강화학습의 여러 방법들이 가지고 있는 공통적인 아이디어를 위주로 제시했습니다. 각각의 아이디어는 방법을 변형시킬 수 있는 Dimension으로 볼 수 있습니다. 이러한 Dimension의 집합은 가능한 방법들이 펼쳐진 공간으로 볼 수 있습니다. 이번 Section에서는 방법 공간의 Dimension 개념을 사용하여 지금까지 배운 강화학습의 관점을 요약합니다.
지금까지 배운 강화학습의 방법에는 세 가지 공통된 핵심 아이디어가 있습니다. 첫째로, 모든 방법이 Value Function을 추정했습니다. 둘째로, 모든 방법이 실제로 움직인 Trajectory 또는 가능한 State의 Trajectory를 따라 값을 Backup했습니다. 마지막으로 모든 방법이 Generalized Policy Iteration의 전략에 기반했습니다.
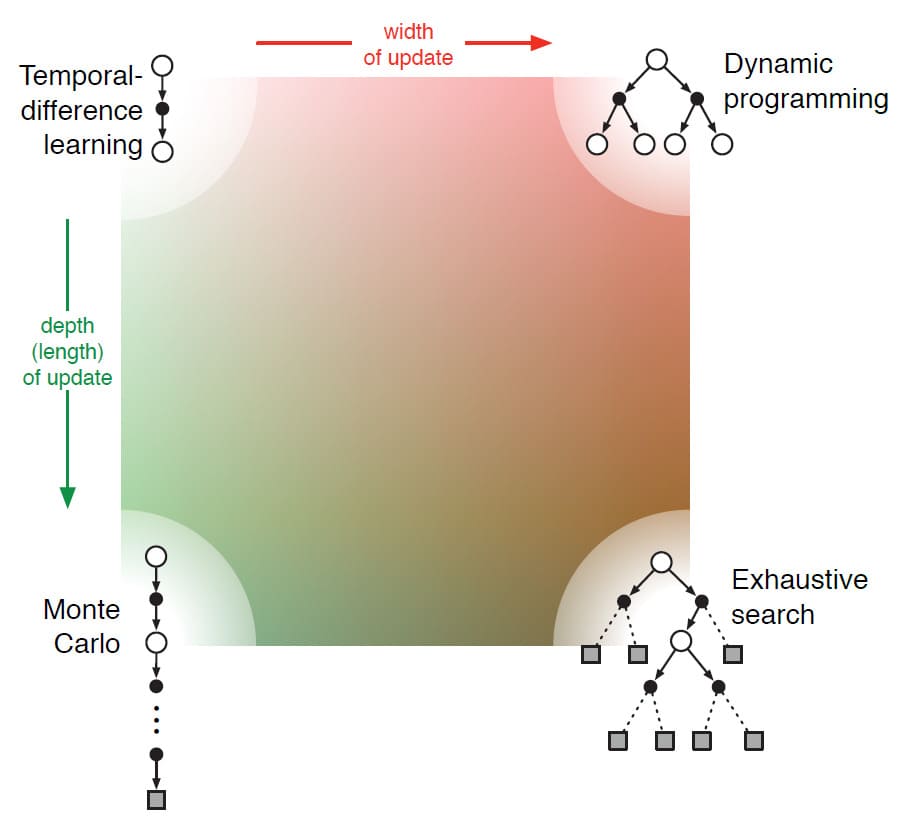
위의 그림을 보시면 방법을 분류하는 가장 핵심적인 두 가지 Dimension이 나와 있습니다. 두 Dimension은 Value Function을 개선하는데 사용되는 Update의 종류와 관련되어 있습니다. 가로 방향은 Sample Update인지 Expected Update인지에 대한 여부입니다. Expected Update는 Distribution Model이 필요한 반면, Sample Update에는 Sample Model만 필요하거나 아예 Model이 없는 Real Experience에서도 수행할 수 있습니다. 세로 방향은 Update의 깊이, 즉 Bootstrapping에 대한 정도를 나타냅니다. 위 그림의 네 꼭지점을 보시면 그 중 세 지점에는 Value Function을 추정하는 방법인 Dynamic Programming, Temporal Difference Learning, 그리고 Monte Carlo Method가 나와 있습니다. Temporal Difference Learning과 Monte Carlo Method 사이에는 그림에는 나와있지 않지만 $n$-step TD 방법이 있으며, Bootstrapping을 많이 할수록(즉, $n$의 값을 커질수록) Monte Carlo에 가까워집니다.
Dynamic Programming은 1-step Expected Update를 포함하기 때문에 맨 오른쪽 상단 끝에 위치합니다. 오른쪽 하단 끝은 Expected Update가 매우 깊어 마지막 State까지 실행되는 극단적인 경우입니다. 이것은 사실상 모든 경우의 수를 체크하는 방법이기 때문에 Exhaustive Search라고 부릅니다. 이 극단적인 방법들 사이에는 Heuristic Search 방법과 제한된 깊이까지 검색하고 Update 하는 방법이 포함됩니다. Dynamic Programming과 Temporal Difference Learning 사이에는 Expected Update와 Sample Update를 혼합하는 방법, 그리고 단일 Update에서 Sample과 Distribution을 혼합하는 방법이 포함됩니다.
이 두 가지 Dimension 외에 마지막으로 논의할 수 있는 세 번째 Dimension은 On-policy와 Off-policy에 대한 구분입니다. On-policy는 현재 사용하는 Policy에 대한 Value Function을 학습하지만, Off-policy는 가장 좋다고 판단되는 다른 Policy로부터 현재 Policy의 Value Function을 학습합니다. Policy를 생성하는 것은 일반적으로 탐색의 필요성으로 인해 현재 가장 좋다고 생각하는 것과 다릅니다. 이 세 번째 Dimension은 위의 그림에 직접적으로 표시되지는 않았으나, 그 그림의 평면에서 수직으로 표현된다고 보시면 됩니다. 이 외에도 이 교재에서는 아래와 같이 여러 가지 다른 Dimension을 구분해놓았습니다.
- Definition of Return : Episodic Task인가, 또는 Continuing Task인가? 그리고 Discount 되는가?
- Action value vs State value vs Afterstate value : 어떤 종류의 Value를 추정해야 하는가?
- Action Selection/Exploration : Exploration과 Exploitation을 적절히 조절하기 위해 어떻게 Action을 선택해야 하는가? (ex. $\epsilon$-greedy, soft-max, upper confidence bound)
- Synchronous vs Asynchronous : 모든 State에 대한 Update를 동시에 수행할 것인가, 아니면 순서에 따라 하나씩 수행할 것인가?
- Real vs Simulated : Real Experience으로 Update할 것인가? 아니면 Simulated Experience으로 Update할 것인가? 또는 둘 다인가? 둘 다라면 어떤 방법으로 융합하는가?
- Location of Updates : 어떤 State, 또는 State-Action 쌍을 Update 하는가? (Model이 없는 방법은 실제로 발생한 State와 State-Action 쌍만 가능하지만 Model에 기반한 방법은 임의로 선택할 수 있음)
- Timing of Updates : Update는 Action 선택의 일부로 수행하는가? 아니면 나중에 수행하는가?
- Memory for Updates : Update된 값을 얼마나 유지해야 하는가? Heuristic Search에서와 같이 Action을 선택할 동안에만 유지하고 폐기할 것인가, 아니면 영구적으로 유지할 것인가?
물론 이러한 Dimension의 구분은 완전하지 않고, 서로 독립적이지도 않습니다. 각각의 개별 알고리즘들은 이 외에도 여러 차이가 있으며, 많은 알고리즘은 여러 개의 Dimension에 걸쳐 있습니다. 예를 들면, Dyna 방법은 Real Experience와 Simulated Experience를 모두 사용하여 동일한 Value Function에 영향을 끼칩니다. 물론 이와 다르게 여러 개의 Value Function을 사용하는 것도 합리적인 방법입니다. 이 Section에서 논하고자 하는 것은 가능한 방법들의 분류 방식을 소개하고 새로운 방법이 나왔을 때, 또는 새로운 방법을 만들고자 할 때의 아이디어를 정리하는 것입니다.
하지만 1부에서 언급하지 않은 가장 중요한 Dimension이 하나 있습니다. 2부에서는 Function Approximation이라는 새로운 아이디어를 본격적으로 다룰 예정입니다.
8장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!

Leave a comment