Arrays and Structures (3)
Strings
The Abstract Data Type
이번 포스트에서는 문자열(String)에 대해 자세히 다뤄보겠습니다, 먼저 문자열에 대한 명확한 정의는 다음과 같습니다.
Definition A string is a finite sequence of zero or more characters, $S = s_0, \ldots, s_{n-1}$ where $s_i$ are characters.
간단하게 설명하자면, 문자를 여러 개 나열한 것이 문자열이라는 것입니다. 문자열에 대한 추상 데이터 타입(ADT)는 다음과 같이 나타낼 수 있습니다.
ADT String is
Object : a finite sequence of zero or more characters.
Functions :
for all s, t ∈ String, i, j, m ∈ non-negative integers
String Null(m) ::= return a string whose maximum length is m characters, but is initially set to NULL. We write NULL as ""
Integer Compare(s, t) ::= if s equals t return 0
else if s precedes t return –1
else return +1
Boolean IsNull(s) ::= if (Compare(s, NULL)) return FALSE
else return TRUE
Integer Length(s) ::= if (Compare(s, NULL))
return the number of characters in s else return 0
String Concat(s, t) ::= if (Compare(t, NULL))
return a string whose elements are those of s followed by those of t
else return s
String Substr(s,i,j) ::= if ((j>0) && (i+j-1)<Length(s))
return the string containing the characters of s at positions i, i+1,…. i+j-1
else return NULL
end String
Strings in C
C 언어는 다른 프로그래밍 언어와 다르게 문자열 변수라는 것이 존재하지 않습니다. 그렇기 때문에 C 언어에서는 어쩔 수 없이 문자형 변수의 배열을 이용하여 문자열을 저장합니다. 문자열의 마지막은 널(NULL) 문자를 이용하여 나타냅니다. C 언어에서 문자열을 저장하는 방법은 다음과 같습니다.
#define MAX_SIZE 100
char s[MAX_SIZE] = "dog";
char t[MAX_SIZE] = "house";
그러나 이런 방식으로 저장하면 문자열의 길이에 비해서 배열의 크기가 너무 커서 저장 공간이 낭비되는 문제가 있습니다. 따라서 이를 해결하기 위해 다음과 같은 대안을 생각해볼 수 있습니다.
char s[] = "dog";
char t[] = "house";
이 경우, 각 배열의 크기는 문자열의 길이에 맞게 정해집니다. 배열 s와 t의 내부는 다음과 같이 저장됩니다.
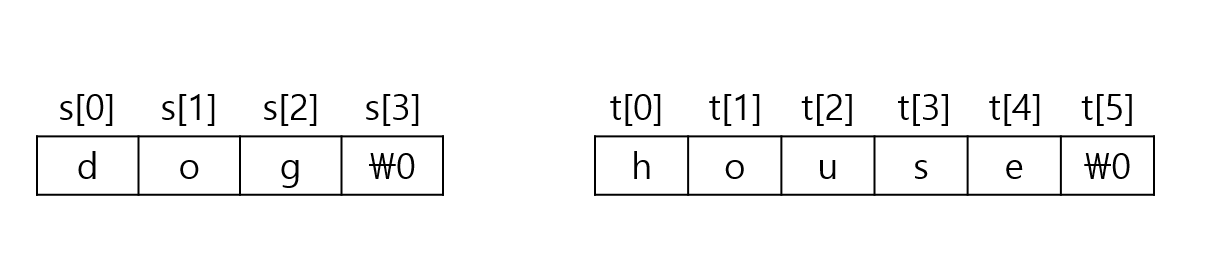
다만 이렇게 문자열의 길이에 맞게 배열의 크기를 정한 경우, 문자열 연산을 사용할 때 문제가 발생하지 않을지 고민해봐야 합니다. 예를 들어, strcat(s, t)라는 연산을 하게 되면 문자열 s와 t를 연결한 문자열이 s에 저장됩니다. (위의 예제에서는 “doghouse”) 그러나 배열 s의 크기는 이미 4로 정해진 상황입니다. 원래대로라면 문제가 발생하겠지만, 다행히도 대부분의 C 컴파일러는 이 경우 추가되는 문자열을 저장할 수 있도록 메모리의 크기를 자동적으로 늘려주는 기능을 갖고 있습니다.
다음은 문자열 함수 중 문자열 복사 함수인 strcpy와 문자열 연결인 strcat을 활용한 간단한 프로그램입니다.
Program 2.12 String insertion function
void strnins(char *s, char *t, int i){
char string[MAX_SIZE] = "", *temp = string;
if (i<0 && i>strlen(s)) {
fprintf(stderr, "Position is out of bounds\n");
exit(1);
}
if (!strlen(s))
strcpy(s, t);
else if (strlen(t)) {
strncpy(temp, s, i);
strcat(temp, t);
strcat(temp, (s + i));
strcpy(s, temp);
}
}
strnins 함수는 매개변수로 문자열 s, t와 정수 i를 받습니다. 이 함수는 문자열 t를 문자열 s의 i번째 위치에 삽입하는 기능을 갖고 있습니다. main 함수에서 첫 번째 문자열 매개변수로 “amobile”, 두 번째 문자열 매개변수는 “uto”를 삽입하고 i는 1로 설정하였습니다. 이 때 함수 strnins는 배열 인덱스 1의 위치(즉, a 다음 위치)에 “uto”를 삽입합니다. 따라서 함수 strnins를 호출한 후 string1에는 “automobile”이 저장됩니다. 이 과정을 그림으로 나타내면 다음과 같습니다.

예시와 같이 매개변수가 들어갈 경우, 첫 번째 if와 두 번째 if에 모두 걸리지 않기 때문에, else if 부분만 보시면 됩니다. 위의 그림은 else if 안에 있는 각각의 문자열 연산이 수행됨에 따라 temp 변수가 어떻게 변하는지 나타내고 있습니다.
strnins 함수에 main 함수를 포함하여 전체 프로그램을 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_SIZE 100
void strnins(char *s, char *t, int i);
int main() {
char string1[MAX_SIZE] = "amobile";
char string2[MAX_SIZE] = "uto";
strnins(string1, string2, 1);
printf("%s\n", string1);
return 0;
}
void strnins(char *s, char *t, int i){
char string[MAX_SIZE] = "", *temp = string;
if (i<0 && i>strlen(s)) {
fprintf(stderr, "Position is out of bounds\n");
exit(1);
}
if (!strlen(s))
strcpy(s, t);
else if (strlen(t)) {
strncpy(temp, s, i);
strcat(temp, t);
strcat(temp, (s + i));
strcpy(s, temp);
}
}
Pattern Matching
패턴 매칭(Pattern Matching)은 어떤 특수한 문자열이, 다른 문자열 내에 포함되어 있는지를 검사하는 작업입니다. 예를 들어, “ababbaabaa”라는 문자열이 있는데, 여기에 “aab”라는 문자열이 포함되어 있는가? 라는 질문에 예/아니오로 답해야하는 문제입니다. 이 경우, “ababbaabaa”에는 “aab”가 포함되어 있기 때문에 예 라는 답이 나옴을 알 수 있습니다.
사실 이 기능은 C 언어에 이미 strstr이라는 함수로 구현되어 있습니다. 이 함수를 사용해 패턴 매칭을 찾는 방법은 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
#include <string.h>
#define MAX_SIZE 100
int main() {
char pat[MAX_SIZE] = "aab";
char string[MAX_SIZE] = "ababbaabaa";
char* t;
if (t = strstr(string, pat))
printf("The string from strstr is: %s", t);
else
printf("The pattern was not found with strstr");
return 0;
}
strstr(string, pat) 함수는 만약 문자열 pat이 문자열 string에 존재하지 않는다면 NULL 포인터를 반환하고, 존재한다면 pat을 포함한 문자열의 시작 주소를 반환합니다. 예를 들어, 위의 프로그램을 실행한다면 string에서 pat이 포함된 부분부터 문자열 끝까지 출력하기 때문에 aabaa를 출력합니다.
그러나 여기에서는 strstr 함수를 사용하지 않고 직접 패턴 매칭 함수를 구현하는 것을 목표로 합니다. 그 이유는 (1) 컴파일러에 따라 strstr 함수를 사용하지 못할 수도 있고, (2) 패턴 매칭을 구현하는 방법은 여러 가지가 있기 때문입니다. 간단한 문제처럼 보이지만, 효율적으로 구현하려면 꽤 복잡한 과정을 거치게 되므로, 여기에서 단계별로 프로그램을 구현해보겠습니다.
먼저 가장 간단한 방법을 생각해봅시다. 문자열 string에서 각각의 index i마다 pat의 문자열을 대조해보면서 포함되어 있는지 확인하는 방법이 있습니다. pat과 string이 위의 프로그램과 같게 설정되어 있다고 가정하면, string[0]~string[2]이 aab인지, string[1]~string[3]이 aab인지, … 이렇게 string 배열을 끝까지 탐색하면서 찾는 방법입니다. 이 방법은 구현이 매우 간단하지만, string의 길이를 m, pat의 길이를 n이라고 할 때 시간 복잡도가 $O(mn)$이 됩니다.
따라서 시간 복잡도를 줄일 수 있는 방법을 생각해봐야 합니다. 우선 다음 두 가지를 고려해볼 수 있습니다.
- 만약 string에 남은 글자 수가 pat의 글자 수보다 작은 경우 확인하지 않고 종료
- 문자열 비교를 수행할 때, 먼저 pat의 첫 글자와 마지막 글자를 비교해본 후 나머지 글자 비교
이 아이디어를 토대로 패턴 매칭 함수인 nfind를 구현해보겠습니다.
Program 2.13 Pattern matching by checking end indices first
int nfind(char* string, char* pat)
{
/* match the last character of the pattern first, and then match from the beginning */
int i, j, start = 0;
int lasts = strlen(string) - 1;
int lastp = strlen(pat) - 1;
int endmatch = lastp;
for (i = 0; endmatch <= lasts; endmatch++, start++) {
if (string[endmatch] == pat[lastp])
for (j = 0, i = start; j < lastp && string[i] == pat[j]; i++, j++)
;
if (j == lastp) return start; /* successful */
}
return -1;
}
nfind 함수는 주어진 문자열에서 패턴이 시작되는 index를 반환하고, 찾지 못한 경우 -1을 반환합니다. 함수 nfind의 동작 과정을 그림으로 표현하면 다음과 같습니다.
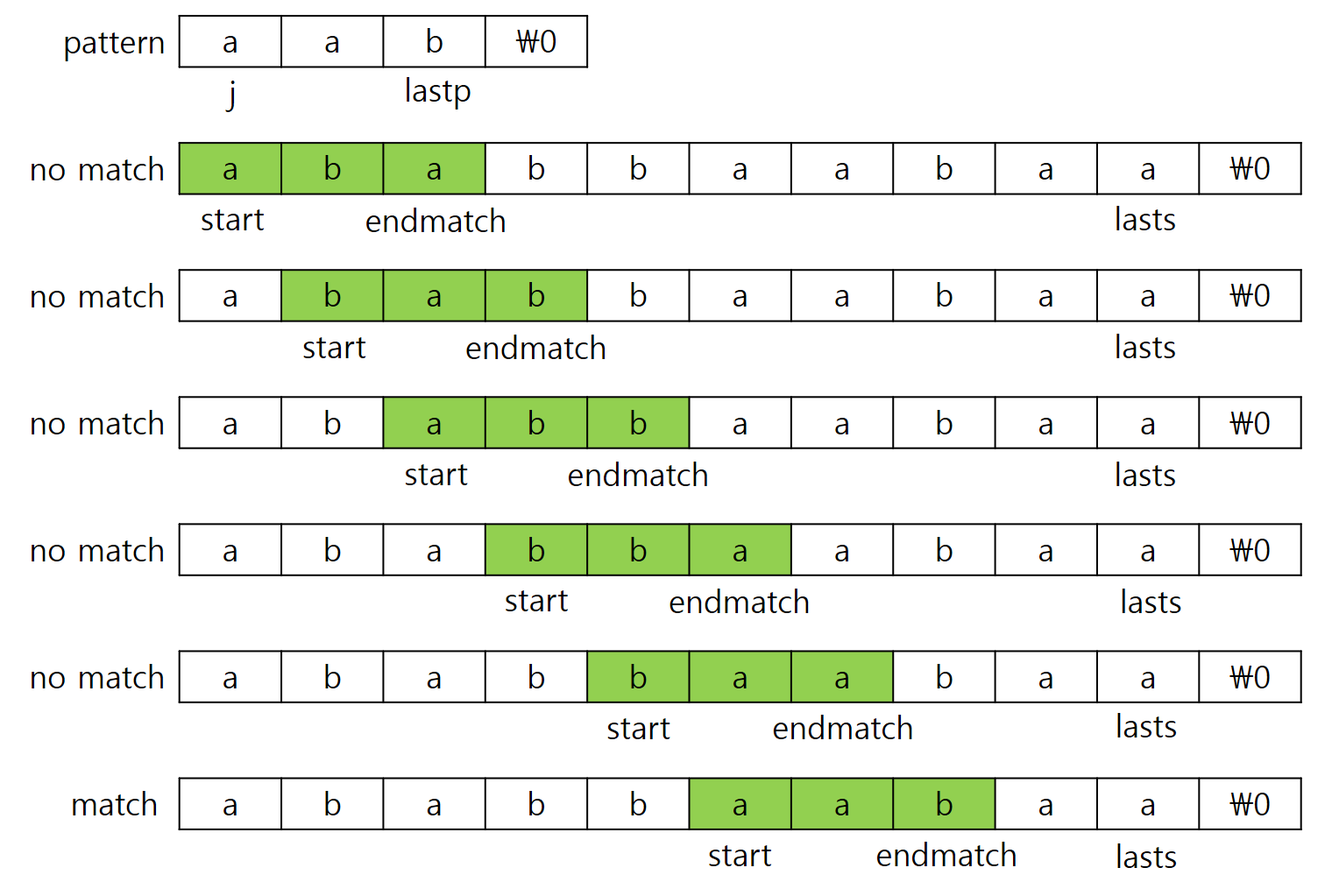
nfind 함수에 main 함수를 포함하여 전체 프로그램을 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <stdio.h>
#include <string.h>
#define MAX_SIZE 100
int nfind(char* string, char* pat);
int main() {
char pat[MAX_SIZE] = "aab";
char string[MAX_SIZE] = "ababbaabaa";
int t;
t = nfind(string, pat);
if (t != -1)
printf("The index number in string where the pattern starts: %d", t);
else
printf("The pattern was not found with nfind");
return 0;
}
int nfind(char* string, char* pat)
{
/* match the last character of the pattern first, and then match from the beginning */
int i, j, start = 0;
int lasts = strlen(string) - 1;
int lastp = strlen(pat) - 1;
int endmatch = lastp;
for (i = 0; endmatch <= lasts; endmatch++, start++) {
if (string[endmatch] == pat[lastp])
for (j = 0, i = start; j < lastp && string[i] == pat[j]; i++, j++)
;
if (j == lastp) return start; /* successful */
}
return -1;
}
이제 nfind가 기존보다 얼마나 효율적으로 변했는지 계산해보겠습니다. 우선 string이 “aa…a”로 주어지고, pat가 “aa…ab”로 주어진 경우 pat의 처음과 끝만 비교하고 넘어가기 때문에 시간 복잡도는 string의 길이에만 의존하는 $O(m)$이 됩니다. 그러나 만약 pat가 “aa…ba”와 같이 주어진 경우에는 처음과 끝이 일치하기 때문에 pat의 마지막 바로 전에 있는 b까지 비교해봐야 하고, 이럴 경우 이전과 다를 바 없는 $O(mn)$의 시간 복잡도를 갖게 됩니다.
따라서 시간 복잡도를 줄이기 위해서는 다른 방법이 필요합니다.
주어진 문자열이 위와 같이 string = “ababbaabaa”, pat = “aab”라고 가정해봅시다. 이 때, 맨 먼저 string[0]~string[2] 부분과 “aab”를 비교해보면 당연히 문자열이 일치하지 않습니다. 그런데, string[0]~string[2] 부분은 “aba”이기 때문에, string[1]~string[3]은 일단 문자열이 b로 시작한다는 것을 알 수 있습니다. 그러면 이런 경우 나머지를 비교해보지 않아도 당연히 일치하지 않을테니 건너뛸 수 있지 않을까? 하는 생각이 듭니다. 첫 글자부터가 다른걸 이미 알고 있는데, 굳이 나머지를 비교할 필요가 없으니까요.
이 과정을 명확하게 하기 위해 다음과 같은 정의를 먼저 제시하겠습니다.
Definition If $p = p_0 p_1 p_2 \cdots p_{n-1}$ is a pattern, then its failure function, $f$ , is defined as:
\[f(j)= \begin{cases} \text{largest } i<j \text{ such that } p_0 p_1 \cdots p_i = p_{j-i} p_{j-i+1} \cdots p_j, & \mbox{if such an }i \ge 0\mbox{ exists} \\ -1, & \mbox{otherwise} \end{cases}\]정의만으로 $f(j)$의 정의가 잘 감이 안오실겁니다. 쉽게 예를 들어서 pat = “abcabcacab”로 가정하고 각각의 $j$에 대하여 $f(j)$를 계산해봅시다.
$f(j)$를 계산하는 방법은 생각보다 간단합니다. 먼저 $j = 0$일 때는 $i < j$를 만족하는 $i \ge 0$이 존재하지 않으니 such that 부분을 볼 필요도 없이 $f(0) = -1$이 나옵니다. $j = 1$일 때는 가능한 $i$가 0밖에 없으므로 $i = 0$만 체크해보면 됩니다. $i = 0$일 때 such that 부분은 $p_0 = p_1$이 되는데, $a \ne b$ 이므로 $f(1) = -1$이 됩니다. 마찬가지로 $j = 2$일 때 가능한 $i$는 0, 1이므로 이 두개를 체크해야 합니다. $i = 0$인 경우 $p_0 = p_2$이 성립해야 하는데 $a \ne c$이므로 해당되지 않고, $i = 1$인 경우 $p_0 p_1 = p_1 p_2$인지 확인해봐도 $ab \ne bc$이므로 $f(2) = -1$임을 알 수 있습니다.
이번에는 $j = 3$일 때 계산해봅시다. 가능한 $i$는 0, 1, 2입니다. $i = 0$인 경우 $p_0 = p_3$이 되는데, $a = a$이므로 드디어 통과가 됨을 알 수 있습니다. 하지만 $i = 1$인 경우 $p_0 p_1 = p_2 p_3$이 성립해야 하는데, $ab \ne ca$이므로 X, $i = 2$인 경우 $p_0 p_1 p_2 = p_1 p_2 p_3$이 성립해야 하는데 $abc \ne bca$이므로 역시 X임을 알 수 있습니다. 즉, 가능한 최대의 $i$값은 0이 되므로 $f(3) = 0$이 되는 것입니다. 이런 방법으로 나머지 $f(j)$를 계산해보면 다음과 같이 나타낼 수 있습니다.

그렇다면 failure function의 의미는 무엇일까요? 계산하는 과정을 통해 아셨겠지만, 이것은 패턴 안에서 같은 부분이 얼마나 반복되는지를 확인하는 함수입니다. 예를 든 pat는 abc가 두 번 반복되면서 시작하고 있습니다. 이 경우, 패턴을 비교할 때 굳이 한 칸씩 비교하지 않고, 반복되는 부분은 그만큼 한번에 이동시킴으로써 비교하는 횟수를 줄일 수 있습니다. 따라서 failure function은 패턴을 확인함으로써 다음 비교 시 얼만큼 건너뛸지를 판단하는 함수라고 보시면 됩니다.
이제 pat = “abcabcacab”, string = “babcbabcabcaabcabcabcacabc”으로 주어졌을 때, 실제로 failure function을 사용하여 어떻게 패턴 매칭을 확인하는지 따져보겠습니다.

(1) 먼저 pat[0]과 string[0]을 비교해봅시다. 이 경우, 첫 글자부터 다르기 때문에 나머지를 비교할 필요 없이 바로 다음 단계로 넘어갑니다.

(2) 다음으로 pat[0]과 string[1]을 비교해봅시다. 첫 글자가 같기 때문에 계속 비교를 수행합니다.

(3) 비교를 수행하다보면 pat[3]과 string[4]를 비교할 때 두 문자열이 다르다는 것을 알 수 있습니다. 이 때가 계산해놓은 failure function의 값을 활용할 때입니다. failure function은 현재 pat의 index보다 한 칸 낮은 곳을 확인해야 하는데, 그 값을 확인해보면 f(2) = -1입니다. 따라서 현재까지는 반복된 값이 없다는 의미가 됩니다. 이제 pat과 string의 index를 정해야 하는데, pat의 index는 failure function의 값에 1을 더한 0이 되고, string은 다음 index인 5가 됩니다.

(4) 이제 pat[0]과 string[5]를 비교해봅시다.

(5) 비교를 수행하다보면 pat[7]과 string[12]를 비교할 때 두 문자열이 다르다는 것을 알 수 있습니다. 마찬가지로, 현재 pat의 index보다 하나 낮은 failure function의 값을 확인해야합니다. $f(6)$의 값을 확인해보니 3입니다. 이전과 마찬가지로 pat의 index는 이 값에 1을 더한 4가 되는데, string의 index는 변하지 않고 그대로 12가 유지됩니다.

(6) 이제 pat[4]와 string[12]를 비교하는데, 이번에도 같지 않습니다. 마찬가지로, 현재 pat의 index보다 하나 낮은 failure function의 값을 확인해야합니다. $f(3)$의 값을 확인해보니 0입니다. 이전과 마찬가지로 pat의 index는 이 값에 1을 더한 1이 되는데, string의 index는 변하지 않고 그대로 12가 유지됩니다.

(7) 이제 pat[1]과 string[12]를 비교하는데, 이번에도 같지 않습니다. 마찬가지로, 현재 pat의 index보다 하나 낮은 failure function의 값을 확인해야합니다. $f(0)$의 값을 확인해보니 -1입니다. 즉, 이제는 pat을 다시 처음부터 확인해야 한다는 뜻입니다. pat의 index는 -1에 1을 더한 0이 되고, string의 index는 13으로 증가합니다.

(8) 먼저 pat[0]과 string[13]을 비교해봅시다. 이 경우, 첫 글자부터 다르기 때문에 나머지를 비교할 필요 없이 바로 다음 단계로 넘어갑니다.

(9) 먼저 pat[0]과 string[14]을 비교해봅시다. 이 경우, 첫 글자부터 다르기 때문에 나머지를 비교할 필요 없이 바로 다음 단계로 넘어갑니다.

(10) 먼저 pat[0]과 string[15]을 비교해봅시다. 첫 글자가 같기 때문에 계속 비교를 수행합니다. 그런데 끝까지 수행해봐도 다른 점이 없습니다. 즉, 패턴 매칭을 찾았습니다! 따라서 알고리즘이 종료됩니다.
이러한 방법으로 패턴 매칭을 찾는 알고리즘을 KMP 알고리즘이라고 합니다. KMP는 이 알고리즘을 개발한 사람들인 Knuth, Morris, Pratt의 앞 글자를 따서 붙인 이름입니다. 이 알고리즘은 다음 논문에서 발표되었습니다.
- D. E. Knuth, J. H. Morris, Jr., and V. R. Pratt, “Fast pattern matching in strings,” SIAM J. Comput., vol. 6, no. 2, pp. 323–350, Jul. 1977. [link]
KMP 알고리즘을 C 언어로 구현하면 다음과 같이 작성할 수 있습니다.
Program 2.14 Knuth, Morris, Pratt pattern matching algorithm
int pmatch(char* string, char* pat)
{
/* Knuth, Morris, Pratt string matching algorithm */
int i = 0, j = 0;
int lens = strlen(string);
int lenp = strlen(pat);
while (i < lens && j < lenp) {
if (string[i] == pat[j]) {
i++; j++;
}
else if (j == 0) i++;
else j = failure[j - 1] + 1;
}
return ((j == lenp) ? (i - lenp) : -1);
}
pmatch 함수의 시간 복잡도를 계산해봅시다. while문은 string이나 pat의 끝을 만나게 되면 반복됩니다. 이 때 사용하는 변수는 string의 index를 나타내는 i, pat의 index를 나타나는 j가 있습니다. i는 프로그램 내에서 증가만 하고 감소하지 않기 때문에 최대 string의 길이만큼만 반복할 수 있습니다. j는 failure[j - 1] + 1로 인해 감소될 수 있지만, 프로그램에서 j가 증가할 때는 i도 반드시 증가하기 때문에 j 또한 string의 길이에만 의존한다고 볼 수 있습니다. 따라서 pmatch 함수는 오로지 string의 길이에만 영향을 받으므로, 시간 복잡도는 $O(strlen(string))$, 즉 $O(m)$임을 알 수 있습니다.
그렇다면 이제 failure function을 계산하는데 시간 복잡도가 얼마나 소요되는지 계산해야합니다. pmatch 함수는 failure function이 이미 계산된 상황에서만 사용할 수 있기 때문입니다. 다행히 failure function을 $O(strlen(pat)) = O(n)$ 내에 계산할 수 있는 방법이 연구되었으며, 이 방법을 찾기 위해서는 먼저 failure function을 다음과 같이 재정의해야합니다.
Definition Another definition of failure function
\[f(j)= \begin{cases} -1, & \mbox{if }j = 0 \\ f^m (j-1)+1, & \mbox{where } m \mbox{ is the least integer } k \mbox{ for which } p_{f^k (j-1)+1} = p_j \\ -1, & \mbox{if there is no } k \mbox{ satisfying the above} \end{cases}\]이렇게 재정의된 failure function을 C 언어로 구현하면 다음과 같습니다.
Program 2.15 Computing the failure function
void fail(char* pat)
{
/* compute the pattern’s failure function */
int i, j, n = strlen(pat);
failure[0] = -1;
for (j = 1; j < n; j++) {
i = failure[j - 1];
while ((pat[j] != pat[i + 1]) && (i >= 0))
i = failure[i];
if (pat[j] == pat[i + 1])
failure[j] = i + 1;
else failure[j] = -1;
}
}
fail 함수의 시간 복잡도를 계산해봅시다. 먼저 가장 안쪽에 있는 while 문을 보시면 i의 값은 failure[i]의 값으로 설정됩니다. 그런데 failure function의 정의를 보시면 아시겠지만 failure[i] 값은 절때 i보다 클 수 없습니다. 따라서 while 문을 반복할수록 i의 값은 감소된다고 볼 수 있습니다. i의 값이 재설정되는 부분은 for 문이 시작할 때인데, 이 때 i의 값은 failure[j] = -1로 인해 -1로 초기화되거나 failure[j] = i + 1로 인해 이전 반복에서 1 큰 값으로 초기화됩니다. pat의 길이가 n으로 정의되어 있는데, for 문은 n-1회 만큼만 반복되므로 i값은 최대 n-1만큼만 증감될 수 있습니다. 따라서 while 문은 for 문이 반복되는 동안 아무리 많아야 n-1회 반복되므로, fail 함수의 시간 복잡도는 $O(strlen(pat)) = O(n)$ 임을 알 수 있습니다.
fail 함수, pmatch 함수에 main 함수를 포함하여 전체 프로그램을 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <stdio.h>
#include <string.h>
#define max_string_size 100
#define max_pattern_size 100
int pmatch(char* string, char* pat);
void fail(char* pat);
int failure[max_pattern_size];
int main() {
char pat[max_pattern_size] = "abcabcacab";
char string[max_string_size] = "babcbabcabcaabcabcabcacabc";
int t;
fail(pat);
t = pmatch(string, pat);
if (t != -1)
printf("The index number in string where the pattern starts: %d", t);
else
printf("The pattern was not found with nfind");
return 0;
}
int pmatch(char* string, char* pat)
{
/* Knuth, Morris, Pratt string matching algorithm */
int i = 0, j = 0;
int lens = strlen(string);
int lenp = strlen(pat);
while (i < lens && j < lenp) {
if (string[i] == pat[j]) {
i++; j++;
}
else if (j == 0) i++;
else j = failure[j - 1] + 1;
}
return ((j == lenp) ? (i - lenp) : -1);
}
void fail(char* pat)
{
/* compute the pattern’s failure function */
int i, j, n = strlen(pat);
failure[0] = -1;
for (j = 1; j < n; j++) {
i = failure[j - 1];
while ((pat[j] != pat[i + 1]) && (i >= 0))
i = failure[i];
if (pat[j] == pat[i + 1])
failure[j] = i + 1;
else failure[j] = -1;
}
}
이로써 길었던 배열과 구조체가 끝났습니다. 읽어주셔서 감사합니다!

Leave a comment