Basic Concepts (2)
Data Abstraction
C언어의 기본 데이터 타입(Data Type)은 int, float, char, … 등이 있습니다. 이러한 기본 데이터 타입을 그룹화하여 배열(Array)과 구조체(Structure)라는 방법으로 데이터 타입을 표현할 수도 있습니다. 그런데 데이터 타입의 명확한 정의는 무엇일까요? 교재에는 다음과 같이 정의하고 있습니다.
Definition A data type is a collection of objects and a set of operations that act on those objects.
이를 해석하면 데이터 타입은 객체와 그 객체 위에서 동작하는 연산의 모음이다라는 뜻이 됩니다. 정의대로라면 프로그램을 작성할 때 어떤 데이터 타입을 사용하든 객체와 연산을 고려해야 합니다. 예를 들어 정수 데이터 타입 int는 {0, +1, -1, +2, -2, …, INT_MAX, INT_MIN}의 객체로 구성됩니다. (INT_MAX = 정수 최대값, INT_MIN = 정수 최소값) 정수 데이터 타입은 여러 연산 종류가 있는데, 대표적으로 +, -, *, / 같은 사칙연산이나 % 같은 나머지 연산이 있습니다. 이러한 연산들을 사용할 때는 반드시 언어나 라이브러리 같은 것으로 정의되어 연산 이름/매개 변수/결과 등이 명세되어야 합니다.
데이터 타입에 대한 연산 뿐만 아니라 데이터 타입의 객체가 어떻게 표현되는지 또한 알 필요가 있습니다. 예를 들어, int는 사용하는 컴퓨터에 따라 2바이트로 표현될 수도 있고, 4바이트로 표현될 수도 있습니다.
다만 프로그램을 설계한 사람과는 달리, 프로그램의 사용자들은 데이터 타입의 객체 표현에 대해 모두 알 필요는 없습니다. 설계자에 의해 제공되는 함수를 통해 객체를 처리하는 간접적인 방법이 있기 때문입니다. 이런 개념으로부터 출발한 것이 추상 데이터 타입(Abstract Data Type ; ADT)입니다. 교재에서는 ADT에 대해 다음과 같이 정의하고 있습니다.
Definition An abstract data type is a data type that is organized in such a way that the specification of the objects and the specification of the operations on the objects is separated from the representation of the objects and the implementation of the operations.
이를 해석하면 추상 데이터 타입은 객체의 명세와 그 연산의 명세가 객체의 표현과 연산의 구현으로부터 분리되어 있는 데이터 타입이다라는 뜻이 됩니다. 이러한 명세와 구현 사이를 구별하는 것을 명시적으로 제공하는 프로그래밍 언어도 있습니다. 예를 들어, C++의 클래스(Class)가 이에 해당됩니다. C언어에서는 이런 기능은 없지만, 같은 개념을 사용하여 데이터 타입을 설계하는 것은 가능합니다.
데이터 타입의 함수는 다음과 같은 종류로 구분할 수 있습니다.
- Creator/Constructor (생성자) : 지정된 타입에 맞는 새로운 인스턴스 생성
- Transformers (변환자) : 1개 이상의 다른 인스턴스를 사용하여 지정된 타입의 인스턴스를 생성
- Observers (관찰자)/Reporters (보고자) : 데이터 타입의 인스턴스에 대한 정보를 제공
추상 데이터 타입에 대해 좀 더 자세하게 설명하기 위해, 다음과 같은 예시를 소개합니다.
ADT Natural_Number is
Object : an ordered subrange of the integers starting at zero and ending at the maximum integer (INT_MAX) on the computer
Functions :
for all x, y IN Natural_Number ; TRUE, FALSE IN Boolean and where +, -, <, and == are usual integer operations
Natural_Number Zero() ::= 0
Boolean Is_Zero(x) ::= if (x) return FALSE
else return TRUE
Natural_Number Add(x, y) ::= if ((x+y) <= INT_MAX) return x+y
else return INT_MAX
Boolean Equal(x, y) ::= if (x == y) return TRUE
else return FALSE
Natural_Number Successor(x) ::= if (x == INT_MAX) return x
else return x+1
Natural_Number Subtract(x, y) ::= if (x < y) return 0
else return x-y
end Natural_Number
추상 데이터 타입의 정의는 이름으로 시작합니다. 이 정의에는 객체와 함수가 있습니다. 객체는 정수로 정의되어 있지만, 그 표현에 대해서는 명확한 참조를 하지 않습니다. 함수의 정의에서는 Natural_Number 데이터 타입의 두 원소를 나타내기 위해 x와 y를 사용합니다. 이 정의를 잘 보시면 덧셈(Add), 뻴셈(Subtract) 그리고 같음(Equal) 등의 함수를 사용합니다. 이것은 하나의 데이터 타입을 정의하기 위해, 다른 데이터 타입의 연산자를 사용할 필요가 있기 때문입니다. 각 함수의 정의에서는 결과 데이터 타입을 먼저 작성하고, 함수 이름, 그리고 오른쪽에는 함수의 정의를 작성해야 합니다. 기호 ::=는 오른쪽의 내용으로 정의된다는 뜻입니다.
위의 예제에서 특이한 점은, 연산의 특정 상황이 발생하면 현재의 값을 그대로 반환하게 정의되어 있다는 점입니다. 예를 들어 Add는 x와 y의 합이 INT_MAX보다 크다면 INT_MAX를 반환합니다. 이것은 이 교재의 저자의 선호에 따라 이렇게 표현이 되었지만, 원한다면 오류를 반환하게 설정할 수도 있습니다.
위의 예시는 추상 데이터 타입의 형식적인 정의를 보여주고 있습니다. 이 교재에서는 C언어와 이러한 추상 데이터 타입의 정의와 구분하기 위해, C언어의 정의에서는 소문자로 시작하고 추상 데이터 타입의 정의에서는 대문자로 시작한다고 명시되어 있습니다.
Performance Analysis
프로그램을 완성한 후에는 그 프로그램이 올바르게 작성되었는지 판단하는 기준이 필요합니다. 교재에서는 필수적으로 만족해야하는 기준을 먼저 소개합니다.
- 프로그램이 원래 명세대로 작동하는가? (Does the program meet the original specification of the task?)
- 제대로 작동하는가? (Does it work correctly?)
- 프로그램이 잘 정리되어 있는가? (Is the program well documented?)
- 프로그램이 논리적인 단위를 만들기 위해 함수를 효과적으로 사용하는가? (Does the program effectively use functions to create logical units?)
- 프로그램이 읽을만 한가? (Is the program’s code readable?)
위의 다섯가지 기준들은 프로그램 개발에 있어 반드시 필요한 요소지만, 구체적으로 프로그램을 분석하기 위해 다음 두 가지 기준이 추가됩니다.
- 프로그램이 메인 메모리와 보조 기억 장치를 효율적으로 사용하는가? (Does the program efficiently use primary and secondary storage?)
- 작업에 대한 프로그램의 실행 시간은 허용 가능한 정도인가? (Is the program’s running time acceptable for the task?)
추가된 두 개의 기준은 성능 평가에 초점을 맞추고 있습니다. 성능 평가 방버은 크게 두 가지로 나눌 수 있는데, 이론적인 시간 복잡도와 공간 복잡도를 계산하는 성능 분석(Performance Analysis), 컴퓨터 성능에 기반해 실제 작동 시간을 측정하는 성능 측정(Performance Measurement)로 나뉩니다. 이번 파트에서는 성능 분석만 다루게 되지만, 성능 측정 또한 무시할 수 없는 중요한 부분입니다.
성능 분석에서 사용되는 시간 복잡도와 공간 복잡도에 대한 정의는 교재에 다음과 같이 나와 있습니다.
Definition The space complexity of a program is the amount of memory that it needs to run to completion. and the time complexity of a program is the amount of computer time that it needs to run to completion.
해석하면 공간 복잡도는 프로그램 수행을 완료하는데 걸리는 메모리의 양이고, 시간 복잡도는 프로그램 수행을 완료하는데 걸리는 컴퓨터 시간의 양이라는 뜻이 됩니다. 공간 복잡도부터 구체적으로 살펴보도록 하겠습니다.
Space Complexity
프로그램 수행에 필요한 공간은 다음 요소들로 분류할 수 있습니다.
- 고정적인 공간 요구량(Fixed Space Requirements) : 프로그램의 입출력 횟수에 관계없는 공간 요구량을 의미. 변수 선언, 구조체 선언, 상수 등이 있다.
- 가변적인 공간 요구량 (Variable Space Requirements) : 프로그램의 특정 인스턴스 $I$에 영향받는 공간 요구량을 의미. 이 때, 프로그램 $P$의 인스턴스 $I$에 대한 가변적인 공간 요구량은 $S_P(I)$로 표현한다. 인스턴스 $I$는 보통 입출력의 횟수나 크기, 값 등으로 정해진다. 예를 들어, 입력 $n$에 대해 크기가 $n$인 배열을 생성하는 프로그램이라면 인스턴스는 $n$이 되고, 이것이 그 프로그램의 유일한 인스턴스라면 해당 프로그램의 가변 공간 요구량은 $S_P(n)$이 된다.
임의의 프로그램에서 총 공간 요구량 $S(P)$는 아래의 수식처럼 정의됩니다. 이 때, $c$는 고정적인 공간 요구량을 의미합니다.
\[S(P) = c + S_P(I)\]보통 프로그램의 공간 복잡도를 분석할 때 고정적인 공간 요구량은 크게 신경쓰지 않습니다. 예를 들어, 다음 예제의 프로그램을 살펴보겠습니다.
float abc (float a, float b, float c){
return a + b + b * c + (a + b + c) / (a + b) + 4.00;
}
Example 1.6 함수 abc()의 공간 복잡도를 구하시오.
위의 abc() 함수는 어떤 경우에도 3개의 float 자료형 매개 변수를 넘겨받아 하나의 단순 산술 계산을 반환하는 함수입니다. 변수 a, b, c 중 어떤 값이 변한다고 해도 프로그램의 실행 코드는 동일하므로, 이 프로그램은 고정적인 공간 요구량만 존재합니다. 즉, $S_{abc}(I) = 0$ 입니다.
float sum(float list[], int n) {
float tempsum = 0;
int i;
for (i = 0; i < n; i++)
tempsum += list[i];
return tempsum;
}
Example 1.7 함수 sum()의 공간 복잡도를 구하시오.
위의 sum() 함수는 반환값이 단순하지만, 입력에 배열 list[]가 들어있습니다. 따라서 이 경우에는 배열이 함수로 어떻게 전달되는지에 따라 가변적인 공간 요구량이 달라집니다. 만약 이 프로그램을 구현한 언어가 Call by Value 방식이라면, 함수가 수행되기 전에 배열 전체가 임시 저장소에 복사되므로 $S_{sum}(I) = S_{sum}(n) = n$가 됩니다. 그러나 이 언어가 Call by Reference 방식이라면 배열 복사라 일어나지 않으므로 $S_{sum}(n) = 0$입니다.
float rsum(float list[], int n){
if(n)
return rsum(list, n-1) + list[n-1];
return list[0];
}
Example 1.8 함수 rsum()의 공간 복잡도를 구하시오.
위의 rsum() 함수는 sum() 함수와 역할은 동일하지만, 재귀 호출 방식을 사용했다는 차이가 있습니다. 어셈블리 언어를 공부해보신 분이라면, 함수 호출을 할 때마다 매개 변수, 지역 변수, 그리고 함수 호출이 끝나고 돌아갈 복귀 주소를 저장해야 한다는 것을 알고 계실 겁니다. 각각의 변수를 저장하는데 필요한 공간은 언어마다 차이가 있지만, 만약 4바이트라고 가정한다면 필요한 총 가변적인 공간 요구량은 $S_{sum}(I) = S_{sum}(n) = 12 \times n$이 됩니다. 즉, 이것으로 재귀 호출 방식은 반복문을 사용하는 것보다 공간 복잡도에 있어 불리하다는 것을 알 수 있습니다.
Time Complexity
프로그램 $P$에 소요되는 시간은 $T(P)$로 정의됩니다. $T(P)$는 아래의 두 요소의 합으로 구성되어 있습니다.
- 컴파일 시간(Compile Time) : 인스턴스 특성에 의존하지 않으며, 한 번 컴파일 하면 다시 컴파일 하지 않고도 실행을 여러번 할 수 있음. 공간 복잡도의 고정적인 공간 요구량과 유사함.
- 실행 시간(Execution Time, 또는 Running Time) : 매번 실행할 때마다 걸리는 시간으로, 공간 복잡도의 가변적인 공간 요구량과 유사함.
공간 복잡도와 비슷하게, 시간 복잡도에서는 컴파일 시간은 고려하지 않고, 실행 시간만을 고려합니다. 시간복잡도에서 실행 시간은 $T_P$로 표현하는데, $T_P$는 인스턴스 특성 $n$에 대해 다음과 같은 식으로 정의할 수 있습니다.
\[T_P(n) = c_a ADD(n) + c_s SUB(n) + c_l LDA(n) + c_{st} STA(n)\]여기서 $c_a$, $c_s$, $c_l$, $c_{st}$는 각각의 연산을 수행하는데 필요한 시간을 나타내는 상수이고, $ADD$, $SUB$, $LDA$, $STA$는 인스턴스 특성 $n$에 대해 프로그램을 수행하기 위해 덧셈, 뻴셈, 적재, 저장 연산을 수행하는 횟수입니다. (LDA는 Load Accumulator의 약자이고, STA는 Store Accumulator의 약자입니다.)
사실 프로그램의 실행 시간을 계산할 때, 이렇게 엄격한 계산을 할 필요는 없습니다. 왜냐하면 각각의 연산 시간은 컴퓨터의 성능에 영향을 받기 때문입니다. 컴퓨터에 독립적인 실행 시간을 계산하기 위해서는 먼저 다음의 정의를 알고 넘어갈 필요가 있습니다.
Definition A program step is a syntactically or semantically meaningful program segment whose execution time is independent of the instance characteristics.
정의대로라면, 프로그램 단계(Program Step)는 인스턴스 특성에 상관없이 실행 시간이 결정되는 프로그램의 단위라고 이해하시면 됩니다. 이 단계를 계산하는 가장 간단한 방법은 새로운 정수형 변수 count를 정의하여 프로그램의 단계마다 이를 증가시켜 최종 결과를 확인하는 것입니다. 다음 예제들을 통해 어떤 방식으로 count을 계산하는지 알아보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <stdio.h>
#include <stdlib.h>
float sum(float[], int);
int count = 0;
int main(){
float *list;
int n, i;
printf("list의 크기를 입력하시오 : ");
scanf("%d", &n);
list = (float*)malloc(sizeof(float) * n);
for(i = 0; i < n; i++)
list[i] = (float)i;
sum(list, n);
printf("%d\n", count);
return 0;
}
float sum(float list[], int n){
float tempsum = 0; count++; /* 대입 연산 */
int i;
for (i = 0; i < n; i++){
count++; /* 반복문 for의 루프를 위한 연산 */
tempsum += list[i]; count++; /* 대입 연산 */
}
count++; /* 반복문 for의 마지막 실행 */
count++; /* 반환 연산 */ return tempsum;
}
교재에서는 sum() 함수만 구현했지만, 결과를 보여드리기 위해 main() 함수도 임의로 구현했습니다. sum() 함수의 핵심은 count의 증가가 어디서 이루어지느냐를 확인하는 것입니다. 대입을 위한 연산, 반복문이 돌 때마다 수행하는 증가 연산, 그리고 반환을 위한 연산이 있습니다. n의 값을 바꾸어가며 프로그램을 테스트해보면, 프로그램 단계는 $2n + 3$임을 알 수 있습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <stdio.h>
#include <stdlib.h>
float rsum(float[], int);
int count = 0;
int main(){
float *list;
int n, i;
printf("list의 크기를 입력하시오 : ");
scanf("%d", &n);
list = (float*)malloc(sizeof(float) * n);
for(i = 0; i < n; i++)
list[i] = (float)i;
rsum(list, n);
printf("%d\n", count);
return 0;
}
float rsum(float list[], int n){
count++; /* if 문을 위한 연산 */
if (n) {
count++; /* 반환과 rsum 호출을 위한 연산 */
return rsum(list, n-1) + list[n-1];
}
count++; /* 반환을 위한 연산 */
return 0;
}
역시 마찬가지로 교재와 달리 rsum() 함수를 제외한 나머지 부분을 임의로 구현하였습니다. list 배열의 크기를 바꿔가며 입력함으로써 프로그램 단계가 어떻게 변하는지 쉽게 확인할 수 있습니다. 계산해보면, 프로그램 단계는 $2n + 2$가 됩니다.
공간 복잡도에서는 재귀 호출 방법이 반복문 사용보다 더 많은 공간 요구량를 가지지만, 시간 복잡도에서는 프로그램 단계 수의 큰 차이가 없습니다. 그러나 프로그램 단계의 수가 작다고 해서 실제 프로그램 실행 시간이 더 짧은 것은 아닙니다. 비록 한 단계라도 함수 호출에는 더 많은 실행 시간이 필요하기 때문입니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <stdio.h>
#define MAX_ROWS 10
#define MAX_COLS 10
void add(int [][MAX_COLS], int [][MAX_COLS], int [][MAX_COLS], int, int);
int count = 0;
int main(){
int a[MAX_ROWS][MAX_COLS], b[MAX_ROWS][MAX_COLS], c[MAX_ROWS][MAX_COLS];
int i, j;
for(i = 0; i < MAX_ROWS; i++){
for (j = 0; j < MAX_COLS; j++){
a[i][j] = i + j;
b[i][j] = i * j;
}
}
add(a, b, c, MAX_ROWS, MAX_COLS);
printf("%d\n", count);
return 0;
}
void add(int a[][MAX_COLS], int b[][MAX_COLS], int c[][MAX_COLS], int rows, int cols){
int i, j;
for(i = 0; i < rows; i++){
count++; /* 첫 번째 for문을 위한 연산 */
for (j = 0; j < cols; j++){
count++; /* 두 번째 for문을 위한 연산 */
c[i][j] = a[i][j] + b[i][j];
count++; /* 대입을 위한 연산 */
}
count++; /* 두 번째 for문의 마지막 연산 */
}
count++; /* 첫 번째 for문의 마지막 연산 */
}
add() 함수는 2차원 배열 a와 b의 합을 계산하여 그 결과를 2차원 배열 c에 저장하는 함수입니다. 함수 입장에서 보면, 세 2차원 배열은 $row \times col$의 크기를 가집니다. 이것으로 프로그램 단계를 계산해보면, $2 \times rows \times cols + 2 \times rows + 1$이 됨을 알 수 있습니다. 이 계산 결과를 토대로, 만약 $rows \gg cols$인 경우 행과 열의 순서를 바꾸면 프로그램 단계가 줄어듬을 알 수 있습니다.
Tabular Method
지금까지 프로그램 단계를 계산하기 위해서는 프로그램 내에 count 같은 변수를 삽입하여 함수를 실행해보는 방식을 사용했습니다. 그러나 모든 프로그램에 이러한 count 함수를 삽입하면서 프로그램 단계를 계산할 수는 없습니다. 단순히 이것을 계산하기 위해 별도의 함수를 선언하는 것도 공간의 낭비이고, 연산이 일어날 때마다 count 변수를 증가시키는 것도 프로그램에서는 쓸데없는 연산만 추가하는 것이기 때문입니다.
프로그램을 수정하지 않고 단계 수를 계산하는 방법으로 테이블 방법(Tabular Method)이 있습니다. 이 테이블에서는 각각의 statement마다 명령문에 대한 단계 수(steps/execution ; s/e), 그 명령문이 실행되는 횟수(Frequency)를 계산해야 합니다. s/e와 Frequency를 곱하면 총 단계 수(Total Steps)를 구할 수 있는데, 총 단계 수를 모두 더하면 전체 함수의 단계 수가 됩니다. 다음 예제들로부터 구체적으로 어떻게 계산하는지를 알아보겠습니다.
Example 1.12 [Iterative Summing of a List of Numbers]
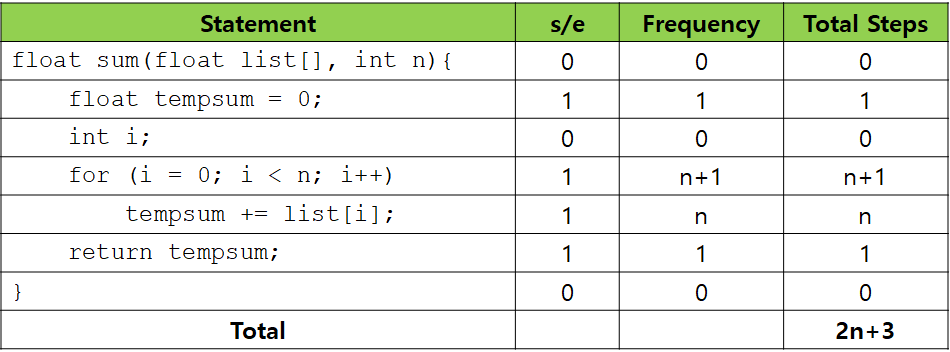
위의 표는 테이블 방법으로 Example 1.9에서 sum() 함수의 프로그램 단계 수를 계산하는 과정을 보여주고 있습니다. 이렇게 테이블 방법을 사용할 때는 s/e를 먼저 다 계산하고, Frequency를 그 다음에 계산하는 것이 좋습니다. for문에서 n번 반복하는 것이 아니라 n+1번 반복한다는 점에 주의하시기 바랍니다. i가 0부터 시작해 n과 같아질 때 빠져나오기 때문입니다. Total Steps은 단순히 s/e와 Frequency를 곱하기만 하면 되고, 총 프로그램 단계 수는 Total Steps를 더하기만 하면 됩니다.
Example 1.13 [Recursive Summing of a list of Numbers]
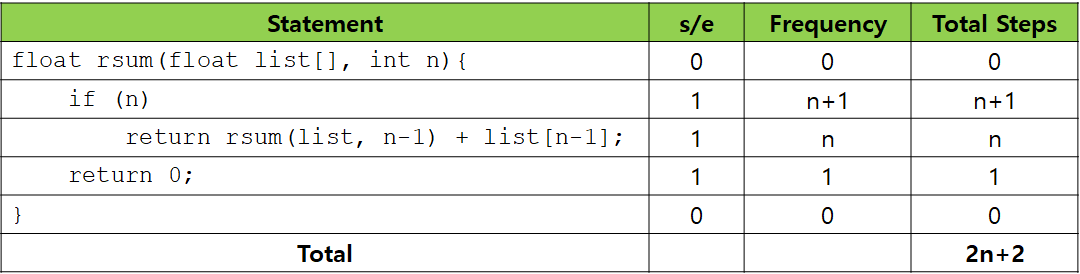
위의 표는 테이블 방법으로 Example 1.10에서 rsum() 함수의 프로그램 단계 수를 계산하는 과정을 보여주고 있습니다. 재귀 호출 함수의 경우 Frequency를 직관적으로 구하기가 힘든 점이 특징입니다.
Example 1.14 [Matrix Addition]
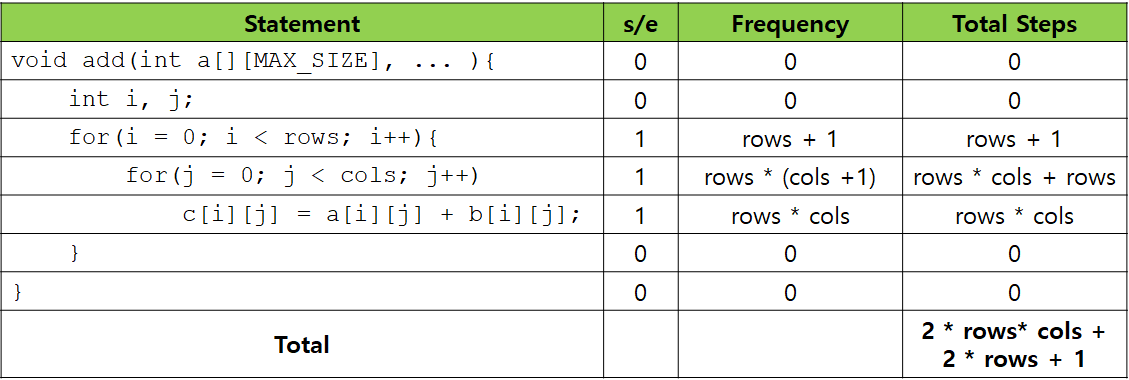
위의 표는 테이블 방법으로 Example 1.11에서 add() 함수의 프로그램 단계 수를 계산하는 과정을 보여주고 있습니다. 무난한 이중 for문이다보니 계산하는데 큰 어려움은 없습니다.
Summary of Time Complexity
- 프로그램의 시간 복잡도는 그 프로그램의 기능을 수행하기 위해 프로그램이 취한 단계의 수로 표현됩니다.
- 프로그램 단계의 수는 인스턴스 특성을 갖는 함수입니다. 인스턴스 특성은 입력의 수, 출력의 수, 입력과 출력의 크기 등으로 정의됩니다.
- 프로그램의 단계 수를 결정하기 전에 어떤 문제의 특성을 사용해야하는지 정확히 알아야 합니다.
- 많은 프로그램에서 시간 복잡성은 지정된 특성에만 의존하지 않습니다. 같은 크기의 입력이라고 하더라도 최상의 경우(Best Case), 최악의 경우(Worst Case), 그리고 평균(Average)에 따라 시간 복잡도가 달라질 수 있습니다.

Leave a comment