Basic Concepts (3)

Asymptotic Notation

지난 포스트에서 시간 복잡도를 계산할 때, 프로그램 단계 수를 체크하여 실행 시간을 계산하였습니다. 이러한 계산의 목적은 같은 기능을 가진 다른 프로그램의 시간 복잡도를 비교하거나, 인스턴스 특성이 변화함에 따라 실행 시간이 어떻게 변하는지를 알아보기 위함이었습니다.

하지만 단순히 프로그램의 단계 수로 실행 시간을 계산하는 것은 정확하지 않을 가능성이 높습니다. 왜냐하면 프로그램의 한 “단계”라는 개념 자체가 모호하기 때문입니다. 예를 들어, x = y와 x = y + z + (x / y) + ( x * y * z - x / t)는 연산의 복잡함의 차이가 있음에도 모두 한 단계로 계산됩니다.

또한 단계 수는 프로그래머에 따라 달라질 수 있습니다. 예를 들어, x = y = z를 x = y와 y = z로 나누어 표현할 수도 있습니다. 즉, 프로그램 단계 수가 $50n$인 것과 $100n$인 것은 큰 차이가 없습니다.

하지만 임의의 상수 $c_1$, $c_2$에 대해 $c_1 n^2$과 $c_2 n$을 비교해봅시다. $c_1$과 $c_2$의 값에 따라 다르겠지만, $n$이 점점 커진다면 결국에는 $c_1 n^2$이 $c_2 n$보다 커지는 시점이 올 것입니다. 이 때의 $n$ 값을 균형 분기점(Break Even Point)라고 합니다. 균형 분기점을 넘는다면, 그 이후의 $n$의 값에 대해서는 항상 $c_1 n^2$이 더 크다는 것은 자명합니다.

이러한 접근 방법으로, 시간 복잡도를 계산하는 새로운 이론인 Big-O 표기법이 등장합니다.

Big-Oh Notation

Definition [Big “O”]  $f(n) = O(g(n))$ iff there exist positive constants $c$ and $n_0$ such that $f(n) \le c g(n)$ for all $n$, $n \ge n_0$

iff는 if and only if를 의미합니다. 고등학교 때 배우는 필요충분조건으로 이해하시면 됩니다. Big-O 표기법을 사용하면 시간 복잡도를 표현하는 것이 굉장히 간단합니다. 어떤 프로그램이든 단계 수의 최고차항만 고려하면 되니까요. 다음의 예제들을 통해 시간 복잡도를 어떻게 계산하는지 알아보도록 하겠습니다.

Example 1.15  다음 프로그램 단계 수의 Big-O 표기법을 구하시오.

• $3n + 2$ : $n \ge 2$일 때 $3n + 2 \le 4n$이므로 $3n + 2 = O(n)$이다.
• $3n + 3$ : $n \ge 3$일 때 $3n + 3 \le 4n$이므로 $3n + 3 = O(n)$이다.
• $100n + 6$ : $n \ge 10$일 때 $100n + 6 \le 101n$이므로 $100n + 6 = O(n)$이다.
• $10n^2 + 4n + 6$ : $n \ge 5$일 때 $10n^2 + 4n + 6 \lt 11n^2$이므로 $10n^2 + 4n + 6 = O(n^2)$이다.
• $1000n^2 + 100n - 6$ : $n \ge 100$일 때 $1000n^2 + 100n - 6 \lt 1001n^2$이므로 $1000n^2 + 100n - 6 = O(n^2)$이다.
• $6 \times 2^n + n^2$ : $n \ge 4$일 때 $6 \times 2^n + n^2 \lt 7 \times 2^n$이므로 $6 \times 2^n + n^2 = O(2^n)$이다.
• $3n + 3$ : $n \ge 2$일 때 $3n + 3 \le 3n^2$이므로 $3n + 3 = O(n^2)$이다.
• $10n^2 + 4n + 2$ : $n \ge 2$일 때 $10n^2 + 4n + 2 \lt 10n^4$이므로 $10n^2 + 4n + 2 = O(n^4)$이다.
• $3n + 2$ : 모든 $n$과 임의의 상수 $c$에 대해 $3n + 2$이 $c$에 대한 균형 분기점이 없으므로 $3n + 2 \ne O(1)$이다.
• $10n^2 + 4n + 2$ : 모든 $n$과 임의의 상수 $c_1$, $c_2$에 대해 $10n^2 + 4n + 2$이 $c_1 n + c_2$에 대한 균형 분기점이 없으므로 $10n^2 + 4n + 2 \ne O(n)$이다.

각각의 Big-O 표기법이 의미하는 바를 알아봅시다. 수학에서 함수를 표현할 때와 같이, $O(1)$은 상수(Constant), $O(logn)$은 로그형(Logarithm), $O(n)$은 선형(Linear), $O(2^n)$은 지수형(Exponential) 등으로 부릅니다. 영어로는 $O(n^2)$과 $O(n^3)$에 대한 표현(Quadratic, Cubic)도 있지만, 한국어로는 딱히 이를 평방형, 입방형으로 부르지는 않습니다.

Big-O 표기법의 정의대로라면 $f(n) = O(g(n))$의 조건은 $n \ge n_0$인 모든 $n$에 대해 $g(n)$이 $f(n)$의 상한이라는 것만 보이면 됩니다. 그 말은 Example 1.15의 $3n + 3$처럼 같은 프로그램 단계라도 여러 Big-O 표기법이 존재한다는 것입니다.

하지만 수학에서 상한을 보일 때 최소상한 말고는 크게 따지지 않는 것과 마찬가지로, Big-O 표기법에서도 일반적으로 가장 작은 Big-O 표기법만을 사용합니다. 즉, $3n + 3$을 Big-O 표기법으로 표현할 때 $O(n)$, $O(n^2)$, $O(n^{10})$, $O(2^n)$ 모두 맞는 표현이지만, 의미를 살리기 위해서 가장 작은 $O(n)$만을 사용한다는 것입니다. 따라서 Big-O 표기법에서 $f(n) = O(g(n))$와 $O(g(n)) = f(n)$은 동일하지 않습니다.

다음의 정리에서는 $f(n)$이 다항함수일 때, Big-O 표기법은 그의 최고차항만으로 결정할 수 있다는 것을 보여줍니다.

Theorem 1.2  If $f(n) = a_m n^m + … + a_1 n + a_0$, then $f(n) = O(n^m)$

Proof

\[f(n) \le \sum_{i=0}^m|a_i|n^i \le n^m \sum_{i=0}^m|a_i|n^{i-m} \le n^m \sum_{i=0}^m|a_i|\]

so, $f(n) = O(n^m)$

□

Omega Notation

Definition [Omega]  $f(n) = \Omega(g(n))$ iff there exist positive constants $c$ and $n_0$ such that $f(n) \ge c g(n)$ for all $n$, $n \ge n_0$

오메가 표기법은 Big-O 표기법의 반대라고 생각하시면 됩니다. Big-O 표기법이 상한을 표현한다면, 오메가 표기법은 하한을 표기합니다. 오메가 표기법을 어떻게 계산하는지 다음 예제를 통해 살펴보도록 하겠습니다.

Example 1.16  다음 프로그램 단계 수의 오메가 표기법을 구하시오.

• $3n + 2$ : $n \ge 1$일 때 $3n + 2 \ge 3n$이므로 $3n + 2 = \Omega(n)$이다.
• $3n + 3$ : $n \ge 1$일 때 $3n + 3 \ge 3n$이므로 $3n + 3 = \Omega(n)$이다.
• $100n + 6$ : $n \ge 1$일 때 $100n + 6 \ge 100n$이므로 $100n + 6 = \Omega(n)$이다.
• $10n^2 + 4n + 2$ : $n \ge 1$일 때 $10n^2 + 4n + 2 \ge 10n^2$이므로 $10n^2 + 4n + 6 = \Omega(n^2)$이다.
• $6 \times 2^n + n^2$ : $n \ge 1$일 때 $6 \times 2^n + n^2 \ge 2^n$이므로 $6 \times 2^n + n^2 = \Omega(2^n)$이다.
• $10n^2 + 4n + 2$ : $n \ge 1$일 때 $10n^2 + 4n + 2 \ge 10n$이므로 $10n^2 + 4n + 6 = \Omega(n)$이다.
• $10n^2 + 4n + 2$ : 임의의 상수 $c$에 대해 $10n^2 + 4n + 2 \ge c$를 만족하는 $n$이 항상 존재하므로 $10n^2 + 4n + 6 = \Omega(1)$이다.
• $6 \times 2^n + n^2$ : $n \ge 993$일 때 $6 \times 2^n + n^2 \ge n^{100}$이므로 $6 \times 2^n + n^2 = \Omega(n^{100})$이다.
• $6 \times 2^n + n^2$ : $n \ge 1$일 때 $6 \times 2^n + n^2 \ge n^2$이므로 $6 \times 2^n + n^2 = \Omega(n^2)$이다.
• $6 \times 2^n + n^2$ : $n \ge 1$일 때 $6 \times 2^n + n^2 \ge n$이므로 $6 \times 2^n + n^2 = \Omega(n)$이다.
• $6 \times 2^n + n^2$ : 임의의 상수 $c$에 대해 $6 \times 2^n + n^2 \ge c$를 만족하는 $n$이 항상 존재하므로 $6 \times 2^n + n^2 = \Omega(1)$이다.

Big-O 표기법과 마찬가지로, 오메가 표기법도 단순히 프로그램 단계 수의 하한만을 의미합니다. 따라서 같은 프로그램 단계 수라도 여러 오메가 표기법이 존재할 수 있지만, 하한의 의미를 살리기 위해서는 최대하한만을 사용하는 것이 좋습니다. 즉, $6 \times 2^n + n^2$의 오메가 표기법은 $\Omega(1)$, $\Omega(n)$, $\Omega(n^2)$, $\Omega(n^{100})$, $\Omega(2^n)$ 모두 맞는 표현이지만, 일반적으로는 $\Omega(2^n)$만을 의미합니다.

다음의 정리에서는 Big-O 표기법과 마찬가지로, $f(n)$이 다항함수일 때, 오메가 표기법은 그의 최고차항만으로 결정할 수 있다는 것을 보여줍니다.

Theorem 1.3  If $f(n) = a_m n^m + … + a_1 n + a_0$ and $a_m \gt 0$, then $f(n) = \Omega(n^m)$

Theta Notation

Definition [Theta]  $f(n) = \Theta(g(n))$ iff there exist positive constants $c_1$, $c_2$ and $n_0$ such that $c_1 g(n) \ge f(n) \ge c_2 g(n)$ for all $n$, $n \ge n_0$

세타 표기법은 Big-O 표기법과 오메가 표기법을 합친 것이라고 보시면 됩니다. 단순히 상한이나 하한만을 고려하는 것이 아니라, $g(n)$이 $f(n)$에 대해 상한과 하한을 모두 가져야만 $f(n) = \Theta(g(n))$가 됩니다. 세타 표기법을 계산하는 방법은 다음 예제를 통해 살펴보도록 하겠습니다.

Example 1.17  다음 프로그램 단계 수의 세타 표기법을 구하시오.

• $3n + 2$ : $n \ge 2$일 때 $3n + 2 \ge 3n$이고, $n \ge 2$일 때 $3n + 2 \le 4n$이므로 $3n + 2 = \Theta(n)$이다.
• $3n + 3$ : $n \ge 3$일 때 $3n + 3 \ge 3n$이고, $n \ge 3$일 때 $3n + 3 \le 4n$이므로 $3n + 3 = \Theta(n)$이다.
• $10n^2 + 4n + 2$ : $n \ge 5$일 때 $10n^2 + 4n + 2 \ge 10n^2$이고, $n \ge 5$일 때 $10n^2 + 4n + 2 \le 11n^2$이므로 $10n^2 + 4n + 2 = \Theta(n^2)$이다.
• $6 \times 2^n + n^2$ : $n \ge 4$일 때 $6 \times 2^n + n^2 \ge 6 \times 2^n$이고, $n \ge 4$일 때 $6 \times 2^n + n^2 \le 7\times 2^n$이므로 $6 \times 2^n + n^2 = \Theta(2^n)$이다.
• $10 \times logn + 4$ : $n \ge e^4$일 때 $10 \times logn + 4 \ge 10 \times logn$이고, $n \ge e^4$일 때 $10 \times logn + 4 \le 11 \times logn$이므로 $10 \times logn + 4 = \Theta(logn)$이다.
• $3n + 2 \ne \Theta(1)$ (상한 조건 불가능)
• $3n + 2 \ne \Theta(n^2)$ (하한 조건 불가능)
• $10n^2 + 4n + 2 \ne \Theta(n)$ (상한 조건 불가능)
• $10n^2 + 4n + 2 \ne \Theta(1)$ (상한 조건 불가능)
• $6 \times 2^n + n^2 \ne \Theta(n^{100})$ (상한 조건 불가능)
• $6 \times 2^n + n^2 \ne \Theta(n^2)$ (상한 조건 불가능)
• $6 \times 2^n + n^2 \ne \Theta(1)$ (상한 조건 불가능)

Big-O 표기법과 오메가 표기법과는 달리, 세타 표기법은 상한과 하한 조건을 동시에 만족해야 하므로 유일하게 존재합니다. $f(n)$이 다항함수인 경우, Big-O 표기법이나 오메가 표기법과 같이 최고차항의 계수만 고려하면 간단하게 세타 표기법을 구할 수 있습니다.

Theorem 1.4  If $f(n) = a_m n^m + … + a_1 n + a_0$ and $a_m \gt 0$, then $f(n) = \Theta(n^m)$

Asymptotic Complexity

지난 포스트에서의 시간 복잡도 분석을 다시 해봅시다. 그 당시에는 프로그램 단계 수만 계산해서 sum() 함수는 $2n +3$라고 결론지었습니다. 이것을 방금 배운 세타 표기법으로 표현하면 $\Theta(n)$이 됨을 알 수 있습니다. 물론 이 때는 프로그램 단계 수를 정확하게 계산하였기 때문에 즉각적으로 세타 표기법으로 변환할 수 있었지만, 실제 프로그램을 보고 바로 Big-O, 오메가, 세타 표기법으로 표현하려고 하면 어떻게 해야 할까요? 결론부터 말씀드리면 이런 표기법으로 시간 복잡도를 표현할 때는 프로그램 단계 수를 ‘정확하게’ 계산할 필요가 없습니다. 프로그램의 각 부분의 시간 복잡도를 먼저 대략적으로 계산한 뒤, 이 것들을 합산하면 됩니다.

Example 1.18 [Complexity of Matrix Addition]

이 방법은 지난 포스트에서 다루었던 테이블 방법(Tabular Method)과 비슷합니다. 하지만 테이블 방법에서 엄격하게 계산했던 Step/Execution, Frequency 등을 오차없이 정확하게 계산하는 것이 아니라, 대략적으로 이정도의 세타 표기법을 갖는다는 것만 보이고 넘어가면 훨씬 간단합니다. 또한 합산할 때도 가장 큰 시간 복잡도만 고려하면 된다는 장점이 있습니다.

Example 1.19 [Binary Search]

지난 포스트에서 나왔던 함수 binsearch()의 시간 복잡도를 점근 표기법으로 구해봅시다. 함수 binsearch()의 인스턴스 특성은 list의 원소의 수 $n$이고, while 루프 내부 연산은 인스턴스 특성에 관여하지 않으므로 시간 복잡도는 $\Theta(1)$임을 알 수 있습니다. while 루프가 반복되는 횟수는 list를 절반씩 줄여나가며 실행되므로, 최악의 경우라도 $\lceil log_2(n+1) \rceil$번만 돌면 끝나게 됩니다. 따라서 최악의 경우를 고려한 시간 복잡도는 $\Theta(logn)$이 됩니다. 만약 한번에 숫자를 찾는 최상의 경우라면 $\Theta(1)$이 됩니다.

Example 1.20 [Permutation]

지난 포스트 마지막에 다룬 순열 알고리즘의 시간 복잡도를 점근 표기법으로 구해봅시다. 함수 perm()의 인스턴스 특성은 list의 길이 $n$입니다. 함수 내부를 한줄한줄 따라가보면, $i = n$일 때 $\Theta(n)$의 시간 복잡도가 소요되고, $i < n$일 때는 else 문으로 넘어가게 됩니다. else문의 for 루프는 $n - i + 1$번 수행되며 for 루프가 한 번 돌때마다 내부의 perm 호출로 인해 $\Theta(n + T_{perm}(i + 1, n))$의 시간이 걸립니다.

$T_{perm}(i + 1, n)$은 $i + 1 \le n$일 때 적어도 $n$번 수행되므로, $i < n$에 대해 $T_{perm}(i, n) =$ $\Theta((n - i + 1) \times T_{perm}(i + 1, n))$이라는 결론이 나옵니다. 이 식을 계산하면 최종적으로 $T_{perm}(i, n)$ $= \Theta(n(n!))$가 됩니다.

Example 1.21 [Magic Square]

이번에는 마방진(Magic Square) 생성 문제의 시간 복잡도를 구해보겠습니다. 마방진은 1부터 $n^2$까지의 자연수를 $n \times n$ 크기의 행렬에 집어넣어 각각의 행, 열, 그리고 주 대각선(Major Diagonal)의 합이 모두 같은 특징을 가지고 있습니다.  예를 들어, 다음은 $n = 5$일 때의 마방진 예시입니다. 이 마방진은 각각의 행, 열, 주 대각선의 합이 65로 동일함을 확인할 수 있습니다.

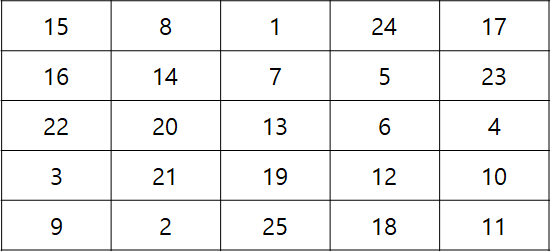
마방진을 만드는 방법은 복잡해 보이지만, $n$이 홀수일 때는 Coxeter의 규칙을 사용하여 쉽게 만들 수 있습니다. 이 규칙에 따르면 먼저 1을 첫째 행 가운데에 놓고, 왼쪽 위 대각선 방향으로 올라가면서 1씩 큰 수를 삽입하는 것입니다. 만약 왼쪽이나 위로 올라갈 수 없다면, 반대편 자리로 이동해서 반복합니다. 예를 들어, 첫째 행 가운데의 1에서 왼쪽 위로 올라갈 수 없으니, 왼쪽 마지막 행에 2를 삽입하는 방식입니다. 만약 다음에 들어갈 자리가 빈 칸이 아니라면, (ex. 5 다음 위치에 1이 채워져 있는 경우) 바로 아래에 다음 번호를 삽입합니다.

위의 $n = 5$일 때의 마방진은 Coxeter의 규칙대로 만들어진 마방진입니다. 생성 과정을 따라가보시면, Coxeter의 규칙이 어떠한지 쉽게 이해할 수 있을 것입니다. 이것을 C언어로 구현하면, 다음과 같이 구현할 수 있습니다.

#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 15    /* 마방진의 최대 크기 */

int main(){
    static int square[MAX_SIZE][MAX_SIZE];
    int i, j, row, column;
    int count;
    int size;
    
    printf("마방진의 크기를 입력하시오 : ");
    scanf("%d", &size);
    
    /* 입력이 최대/최소 크기를 벗어나거나, 짝수면 오류 판정 */
    if( (size < 1) || (size > MAX_SIZE + 1) ){
        fprintf(stderr, "오류 : 크기가 범위를 벗어났습니다.");
        exit(1);
    }
    
    if ( !(size %2) ){
        fprintf(stderr, "오류 : 크기가 짝수입니다.");
        exit(1);
    }
    
    /* 마방진을 0으로 초기화 */
    for(i = 0; i < size; i++){
        for(j = 0; j < size; j++)
            square[i][j] = 0;
    }
    
    /* 첫째 행 가운데에 1을 삽입 */
    square[0][(size-1)/2] = 1;
    
    /* 첫째 행 가운데의 위치를 i, j에 저장 */
    i = 0;
    j = (size - 1) / 2;
    
    /* 반복문을 사용하여 마방진 생성 */
    for (count = 2; count <= size * size; count++){
        row = (i - 1 < 0) ? (size - 1) : (i - 1);       /* 위로 이동 */
        column = (j - 1 < 0) ? (size - 1) : (j - 1);    /* 왼쪽으로 이동 */
        if (square[row][column])                        /* 아래로 이동 */
            i = (++i) % size;
        else {              /* 현재 좌표가 0인 경우 (비어있는 경우) */
            i = row;
            j = (j - 1 < 0) ? (size - 1) : --j;
        }
        square[i][j] = count;
    }
    
    /* 생성된 마방진 출력 */
    printf("크기가 %d인 마방진 생성 결과 :\n", size);
    for(i = 0; i < size; i++){
        for(j = 0; j < size; j++)
            printf("%5d", square[i][j]);
        printf("\n");
    }
}

프로그램을 분석해보면, 첫 2개의 if 문은 모두 $\Theta(1)$, 다음으로 나오는 이중 for 문은 둘다 size에 비례해 반복하므로 $\Theta(n^2)$, 다음 for문은 size * size 만큼 반복하므로 역시 $\Theta(n^2)$, 나머지 부분은 모두 $\Theta(1)$ 만큼의 시간 복잡도가 소요됩니다. 총 시간 복잡도를 계산하면, 가장 큰 부분만 확인하면 되므로,  $\Theta(n^2)$가 됩니다.

지금까지 시간 복잡도를 표현할 때는 가장 엄격한 조건인 세타 표기법을 사용하였지만, 일반적으로 시간 복잡도는 상한만을 많이 고려합니다. 따라서 앞으로는 Big-O 표기법만으로 시간 복잡도를 표현하겠습니다.

Practical Complexities

지금까지는 프로그램의 시간 복잡도를 계산할 때, 인스턴스 특성에 대한 함수로 표현하였습니다. 이런 표현 방법은 인스턴스 특성의 변화에 따라 실행 시간이 어떻게 변하는지, 그리고 같은 작업을 수행하는 두 프로그램을 비교하는데 유용합니다. 예를 들어, 동일한 작업을 수행하는 프로그램 P와 Q에 대해서, P는 시간 복잡도가 $\Theta(n)$이고, Q는 시간 복잡도가 $\Theta(n^2)$이라면, 충분히 큰 $n$에 대해 P가 Q보다 더 빠르다고 말할 수 있다는 뜻입니다.

충분히 크다는 말에 강조를 한 이유는, 실제로 구현한 프로그램의 인스턴스 특성이 충분히 큰 것인가를 확인해야 하기 때문입니다. 만약 프로그램 P가 $10^6n$ms의 수행 시간을 가지고, 프로그램 Q가 $n^2$ms의 수행 시간을 가진다고 가정해봅시다. 시간 복잡도 측면에서는 프로그램 P가 더 우수하지만, 만약 프로그램의 인스턴스 특성이 항상 $n \le 10^6$이라면 프로그램 Q가 더 빠르게 수행될 것입니다.

다음 그림은 인스턴스 특성 $n$에 따라 각 시간 복잡도가 어떻게 변하는지 나타낸 그래프입니다. 비록 그래프 상에서는 지수형태의 시간 복잡도가 결과적으로 가장 높게 나오지만, $n \le 5$인 경우에서는 그렇게 큰 차이가 나지 않음을 알 수 있습니다.

Performance Measurement

이제는 프로그램을 수행할 때 걸리는 실제 시간을 측정해보도록 하겠습니다. 시간을 재는데 필요한 함수는 C언어의 라이브러리인 time.h에 정의되어 있습니다. 시간을 재는 방법은 2가지가 있는데, clock을 사용하는 방법과 time을 사용하는 방법이 있습니다.

clock을 사용하는 방법은 프로그램이 시작하고 난 후부터 소요된 프로세스 시간의 양을 나타냅니다. 시작 시간과 끝나는 시간에 각각 clock을 체크해서, 그 사이에 소요된 clock 수를 계산합니다. 컴퓨터에서는 clock을 실제 시간으로 변환할 수 있는 CLOCK_PER_SEC 이라는 상수가 정의되어 있으므로, clock수를 이 값으로 나누게 되면 실제 시간을 계산할 수 있습니다.

두 번째 방법은 실제 시간을 계산하는 time을 사용하는 방법입니다. clock과 유사하게, 시작 시간과 끝나는 시간을 각각 체크해서, 그 시간차를 계산하면 간단하게 소요 시간을 계산할 수 있습니다. clock을 계산할 필요가 없는 장점이 있습니다.

두 방법 모두 독립적인 자료형을 사용하기 때문에, 실제 초 단위 시간으로 변환하기 위해서는 타입 변환이 필요합니다. 다음은 두 방법의 차이를 간략하게 정리했습니다.

1. clock을 사용하는 방법

• 시작 시간 체크 : start = clock();
• 종료 시간 체크 : end = clock();
• 반환 타입 : clock_t
• 초 단위로 변환 : duration = ((double)(end-start)/CLOCKS_PER_SEC;

2. time을 사용하는 방법

• 시작 시간 체크 : start = time(NULL);
• 종료 시간 체크 : end = time(NULL);
• 반환 타입 : time_t
• 초 단위로 변환 : duration = (double)difftime(end, start);

다음 예제를 통해 정확한 사용 방법을 보여드리겠습니다.

Example 1.22 [Timing for Selection Sort] clock을 사용하여 최악의 경우 시간을 측정할 수 있게 선택 정렬 프로그램을 수정한다.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_SIZE 10000
#define SWAP(x, y, t)  ((t) = (x), (x) = (y), (y) = (t))
void sort(int [], int);  /* 선택 정렬 */
int main(){
    int i, n;
    int list[MAX_SIZE];
    clock_t start, end;
    double duration;
    
    printf("생성할 숫자의 갯수를 입력하시오 : ");
    scanf("%d", &n);
    
    
    if( (n < 1) || n > MAX_SIZE) {      /* 비정상적인 입력에 대한 예외처리 */
        fprintf(stderr, "적절하지 않은 n값입니다.");
        exit(EXIT_FAILURE);
    }
    
    printf("정렬 전 : ");
    for(i = 0; i < n; i++){             /* 입력한 수 만큼 역순으로 데이터 생성 */
        list[i] = n - i;
        printf("%d ", list[i]);
    }
    
    start = clock();                    /* 시작 시간 체크 */
    sort(list, n);                      /* 선택 정렬 수행 */
    end = clock();                      /* 종료 시간 체크 */
    
    printf("\n정렬 후 : ");               /* 정렬 결과 출력 */
    for(i = 0; i < n; i++)
        printf("%d ", list[i]);
    printf("\n");
    
    duration = ((double)(end - start))/CLOCKS_PER_SEC;      /* 소요 시간 초 단위로 변환 */
    printf("소요 시간 : %f\n", duration);       /* 소요 시간 출력 */
    
    return 0;
}

void sort(int list[], int n){
    int i, j, min, temp;
    for (i = 0; i < n-1; i++){
        min = i;
        for (j = i+1; j < n; j++){
            if (list[j] < list[min])
                min = j;
        }
        SWAP(list[i], list[min], temp);
    }
}

리스트에 무작위 수를 삽입했던 선택 정렬과 다르게, 이 예제는 최악의 경우에서의 시간을 측정하는 것이 목표입니다. 선택 정렬에서 최악의 경우는 역순으로 정렬된 상황이기 때문에, 크기를 입력받으면 역순으로 숫자가 배열되게 수정하였습니다. 이후로는 선택 정렬 앞 뒤로 clock을 체크하여 소요시간을 측정하였습니다.

다만 프로그램을 이용해 정확한 시간의 변화를 알아보기 위해서는 같은 인스턴스 특성에 대해 여러 번 실행해 본 다음 평균 값을 계산해야 합니다. 아래의 그래프는 교재의 저자가 실제로 다수의 테스트를 통해 얻은 소요 시간 그래프입니다. Big-O 표기법과 완벽하게 일치하지는 않지만, 대략적으로 $n^2$을 따르는 것을 확인할 수 있습니다.

Generating Test Data

보통 시간 복잡도에서는 최악의 경우를 가정하기 때문에 테스트 데이터도 프로그램에서 발생할 수 있는 최악의 경우가 나오게 생성해야 합니다. 하지만 최악의 경우가 발생하는 데이터를 만드는 것이 쉽지만은 않습니다. 대부분의 경우 프로그램을 사용해서 최악의 경우를 만들 수도 있지만, 이것이 불가능한 문제가 나올 수도 있기 때문입니다.

이런 경우에는 인스턴스 특성 값에 대해 적당히 큰 규모의 무작위 테스트 데이터를 생성하는 수밖에 없습니다. 이러한 테스트 데이터 각각에 대해 실행 시간을 계산하여, 이 중 최대값을 해당 인스턴스 특성 값에 대한 최악의 경우 소요되는 시간으로 판단합니다.

최악의 경우가 아닌 평균적인 경우의 시간을 측정하는 것은 더욱 어렵습니다. 모든 인스턴스 특성에 대해 소요 시간을 계산한 뒤, 이를 평균을 내야 하므로 시간이 굉장히 오래 걸리기 때문입니다. 예를 들어, 정렬 프로그램의 경우에는 모든 데이터가 다르다고 가정했을 시, 인스턴스 특성 $n$에 대해 $n!$ 만큼의 경우의 수가 생깁니다.

최악의 경우이던, 평균적인 경우이던 간에 테스트를 하는 인스턴스의 수는, 실제 모든 경우의 수보다 확실히 적습니다. 그러므로 시간을 측정하는 데이터를 추려내는 작업은 문제에 따라 천차만별이며, 이를 위해서는 전문적으로 알고리즘을 분석하는 작업이 필요합니다. 다만 이 부분을 다루는 것은 본 과목의 범주 외이므로, 여기서는 다루지 않겠습니다.