Is Learning Feasible?

2장은 지난 장의 마지막 이슈였던 학습은 가능한 것인가? 라는 의문을 해결하는 강의입니다.

Outline

이번 장은 총 4부분으로 구성되어 있습니다. 먼저 확률론적으로 예제를 통해 접근하고, 이를 기계학습과 연결하는 과정을 거칩니다. 하지만 이 과정에서 몇 가지의 문제가 생기는데, 이 원인과 그 해결책은 무엇인지까지 다루게 됩니다.

Probability to the rescue

가장 먼저, 위 슬라이드의 오른쪽 그림과 같이 빨간색 구슬과 초록색 구슬이 들어있는 통(Bin)을 생각해 봅시다. 이 통에서 무작위로 구슬을 하나 뽑았을 때, 그 구슬이 빨간색일 확률을 $\mu$라고 한다면 자연스럽게 초록색 구슬을 뽑을 확률은 $1-\mu$이 됩니다. 그런데 문제는, 우리는 이 통에 빨간색 구슬이 얼마나 들었는지 모르기 때문에 정확한 $\mu$은 모르는 상태입니다. 그래서 이를 확인하기 위해, 이 통에서 무작위로 $N$개의 구슬을 뽑기로 했습니다. 뽑은 $N$개의 구슬에서 빨간색 구슬의 비율을 $\nu$라고 정의합니다.

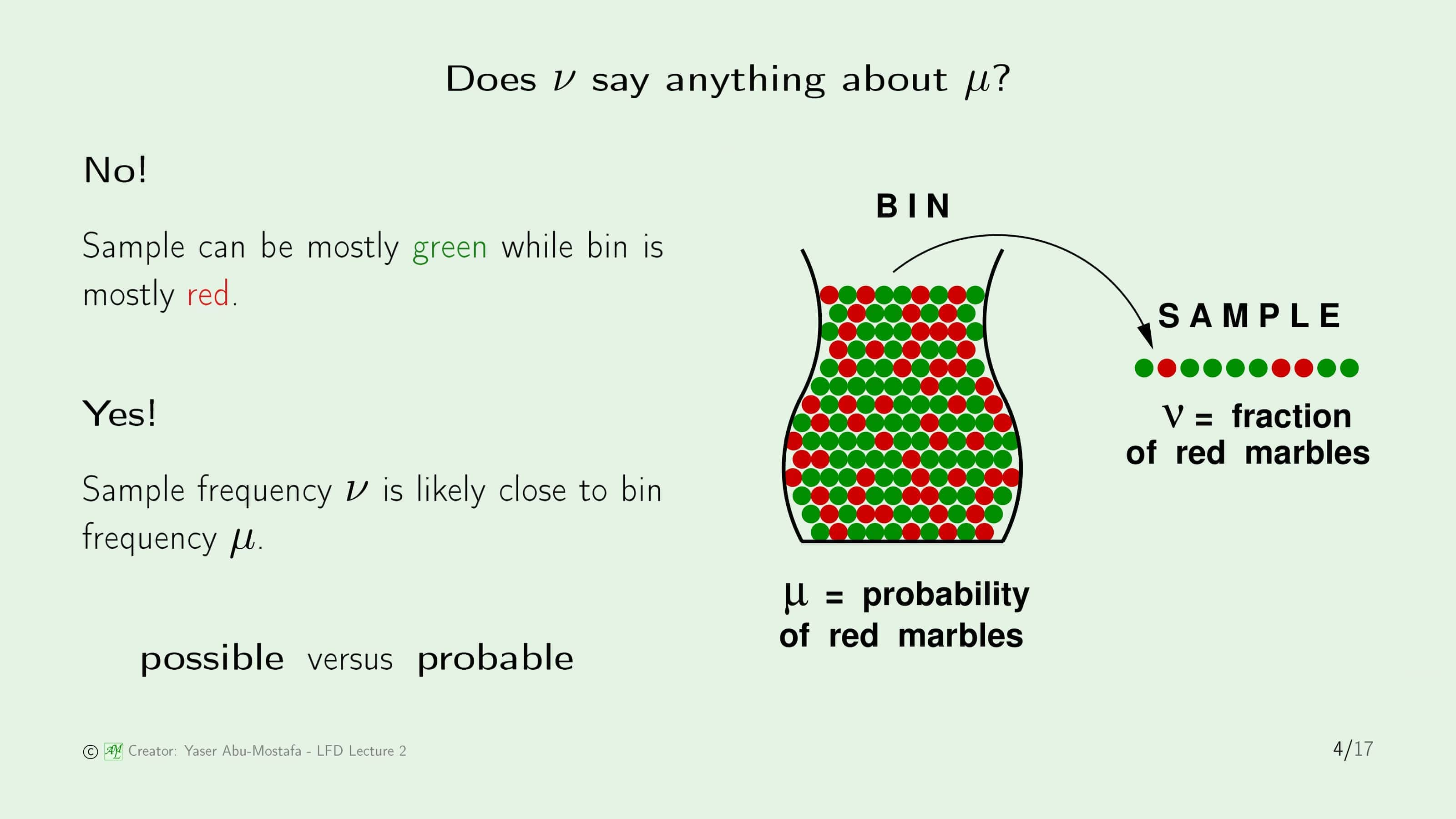
그렇다면 $\nu$를 가지고 $\mu$를 알 수 있을까요? 상황에 따라서 그렇다고 볼 수도 있고, 아닐 수도 있습니다.

먼저, 할 수 없다고 말할 수 있는 이유는 $\nu$는 통에서 일부분만을 꺼낸 구슬이기 때문에, 통에 들어있는 구슬의 비율과 다르게 나올 가능성이 존재합니다. 예를 들어, 통에 빨간색 구슬이 90개, 초록색 구슬이 10개가 들어있다고 가정해봅시다. 이 통에서 무작위로 10개의 구슬을 뽑았을 때, 정말 낮은 확률로 초록색 구슬만 10개가 나올 수도 있습니다. 따라서 이러한 경우엔 $\nu$가 $\mu$와 같다고 말할 수 없습니다. 하지만 만약 한번에 뽑는 구슬의 수가 많아진다면 (다시말해 $N$이 커진다면) $\nu$가 $\mu$와 같지는 않더라고 점점 가까워짐을 알 수 있습니다.

유튜브 강의에서는 이를 가지고 Possible vs Probable 이라 설명합니다. 아마 Possible이라는 것은 $\nu$와 $\mu$가 다를 수 있다는 예제를 말하는 것 같고 Probable이라는 것은 $N$이 커졌을 때 $\nu$와 $\mu$가 가까워 진다는 것을 말합니다.

이전 슬라이드 마지막에서 말했던 것처럼 $N$이 커졌을 때 $\nu$와 $\mu$이 가까워질 수 있다는 것을 알았습니다. 이를 수학적으로 표현한다면 슬라이드에 나와있는 부등식처럼 표현할 수 있습니다. 이를 Hoeffding’s Inequality라고 부릅니다.

이 부등식이 무엇을 의미하는지 하나씩 따져봅시다. 먼저 $| \nu - \mu |$라는 것은 샘플로 뽑은 $N$개의 구슬에서 빨간색 구슬의 비율과 실제 통에 들어있는 구슬에서 빨간색 구슬의 비율의 차이를 의미합니다. 궁극적으로 우리가 원하는 것은 이 둘이 차이가 거의 없는 것이기 때문에 $| \nu - \mu | > \epsilon$의 의미는 우리가 원하지 않는 상황(유튜브 강의에서는 Bad Event로 지칭합니다)으로 볼 수 있습니다. 따라서 왼쪽 항이 의미하는 것은 우리가 원하지 않는 상황(즉, $\nu$와 $\mu$의 차이가 일정 이상 벌어지는 상황)이 일어날 확률을 의미하는 것이 됩니다.

이번엔 오른쪽 항을 분석해 봅시다. 왼쪽 항이 확률을 의미하는 식이었으니 당연히 오른쪽 항은 0과 1 사이의 값이 나와야 합니다. 오른쪽 항은 $\epsilon$과 $N$에 영향을 받는 지수함수이니 이 두 변수에 어떤 값이 들어오는지에 따라 결정됨을 쉽게 알 수 있습니다. 간단하게 표현하면, $\epsilon$과 $N$의 값이 크면 클수록 오른쪽 항의 값이 작아집니다.

이렇게 Hoeffding’s Inequality로 표현한 것을 다른 말로 하면 “$\mu = \nu$”는 P.A.C (Probably Approximate Correct)라 합니다. 쉽게 말하면 “아마 대략적으로 맞다” 라는 것입니다.

이전 슬라이드에서 설명했던 Hoeffding’s Inequality는 모든 $\epsilon$과 $N$에 대해 성립하고, 마침 오른쪽 항은 $\mu$ 에도 영향을 받지 않으니 부등식이 매우 간단해졌습니다. 왜냐하면 $\mu$는 우리가 모르는 값이기 때문에 이게 오른쪽 항에도 있었다면 계산이 상당히 껄끄러웠을 겁니다.

다만 이 부등식이 의미있는 식이 되기 위해서는 오른쪽 항이 0과 1 사이의 값이 되어야 하는데, 이 문제가 조금 복잡합니다. 지수함수 $e^{-2 \epsilon ^{2} N}$의 계수가 2이므로 이 지수함수 $e^{-2 \epsilon ^{2} N}$의 값은 0.5보다 작아야 오른쪽 항이 1보다 작을 수 있습니다. 그런데 이 지수함수 $e^{-2 \epsilon ^{2} N}$의 값이 0.5보다 작아지려면 가급적 지수부분 $2 \epsilon ^{2} N$이 커야 함을 알 수 있습니다. 그런데 여기서 문제가 생기는 것이, $\epsilon$은 $| \nu - \mu |$와 관련이 있으므로 최대한 작게 잡아야합니다. 보통 매우 작은 소수 (예를 들면 0.001)로 정하는데 이걸 제곱까지 해주기 때문에 $N$의 값이 매우매우매우 커야 한다는걸 의미합니다. 다만 여기서는 일단 이 문제는 제쳐놓고, $\nu$와 $\mu$의 값이 유사해진다라는 결론만을 짚고 넘어가겠습니다.

Connection to learning

그럼 지금까지 이야기했던 구슬 문제를 기계학습에 적용시켜 보겠습니다. 통 안에 들어있는 구슬들은 모든 데이터라고 가정해봅시다. (이전 장에서 얘기했던 카드 발급 문제를 예시로 들자면, 카드를 발급하러 신청한 모든 사람들이 통 속의 구슬이 됩니다.) 그리고 통 안에 들어있는 구슬중에 초록색 구슬은 Hypothesis $h$가 정확하게 분류한 데이터(즉, $h(x) = f(x)$), 빨간색 구슬은 Hypothesis $h$가 잘못 분류한 데이터(즉, $h(x) \neq f(x)$)라고 합시다.

이전 장에서 나왔던 그림이 또 나왔습니다. 이 때에는 Traning Examples들이 우리가 모르는 Target Function $f$으로부터 생성된 데이터라고 했지만, 지금까지 기계학습 문제를 확률적인 얘기로 예시를 들었으니, 이 Traning Examples들의 데이터 $x_1, x_2, …, x_N$들이 어떠한 확률 분포(이 확률 분포가 무엇인지는 중요하지 않습니다)를 따른다고 가정한다면 앞부분에서 설명한 구슬 문제에 완벽하게 매칭이 됩니다.

Connection to real learning

그럼 이제 끝난 것일까요? 아쉽게도 그렇지 않습니다. 왜냐면 지금까지 비유를 든 예제는 오로지 특정한 ‘단 하나’의 Hypothesis인 $h$에 대해서만을 가정했기 때문입니다. 이전 장에서 Hypothesis는 한 개가 아니라 set이 존재한다고 했었기 때문에 지금까지 다루었던 가정들을 다른 모든 Hypothesis에 대해서도 마찬가지고 적용해야 합니다. 사족으로, 이렇게 단 하나의 Hypothesis $h$만을 다룬 것은 학습(Learning)이 아니라 검증(Verification)이라고 합니다.

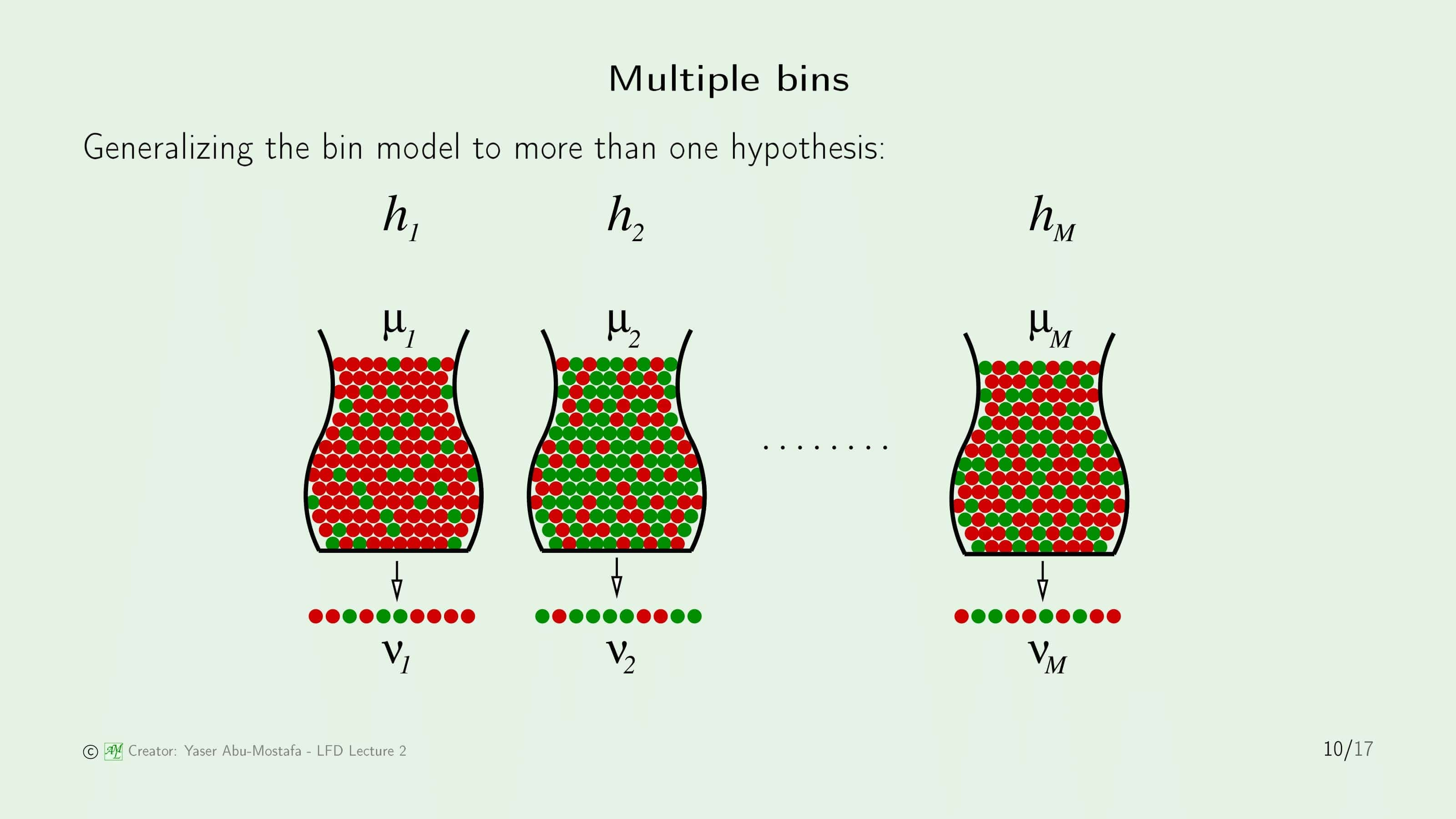
따라서 이를 일반화하기 위해서는, 위 슬라이드의 그림과 같이 많은 통들을 생각해 보아야 합니다. 구슬(데이터)이 빨간색일지 초록색일지는 Hypothesis들에 따라 다르기 때문에 각각의 통에서 뽑아낸 샘플에서의 빨간색 구슬의 비율(=$\nu$)은 각자 다르다는 것을 알 수 있습니다. 이 문제를 쉽게 다루기 위해, 통의 개수는 $M$개로 유한하다고 가정하겠습니다.

이제 구슬의 예제에서 벗어나 완벽하게 학습 문제에 적용시키이 위해, 용어를 좀 바꾸어 보겠습니다. 우리가 직접 뽑은 구슬에서의 빨간색 구슬의 비율 $\nu$를 학습 문제에 매칭시킨다면, Hypothesis $h$가 잘못 분류한 데이터(즉, $h(x) \neq f(x)$)를 의미합니다. 이를 $E_{in} (h)$ (In Sample Error)라고 합니다. 마찬가지로 통 안에 들어있는 전체 구슬 중에 빨간색 구슬의 비율 $\mu$를 학습 문제에 매칭시킨다면, 이를 $E_{out} (h)$ (Out of Sample Error)라고 합니다.

앞으로는 $\nu$와 $\mu$ 기호 대신 $E_{in} (h)$, $E_{out} (h)$를 쭉 사용하게 되니 이 정의를 잘 기억하고 계셔야 합니다. 위 슬라이드 마지막에는 앞에서 설명한 Hoeffding’s Inequality에서 $\nu$와 $\mu$ 기호 대신 $E_{in} (h)$, $E_{out} (h)$를 사용한 식으로 바꾸어 표현하였습니다.

앞의 여러개의 통을 사용한 예시를 $E_{in} (h)$, $E_{out} (h)$를 사용한 표현으로 바꾼 것을 보여주는 슬라이드입니다.

A dilemma and a solution

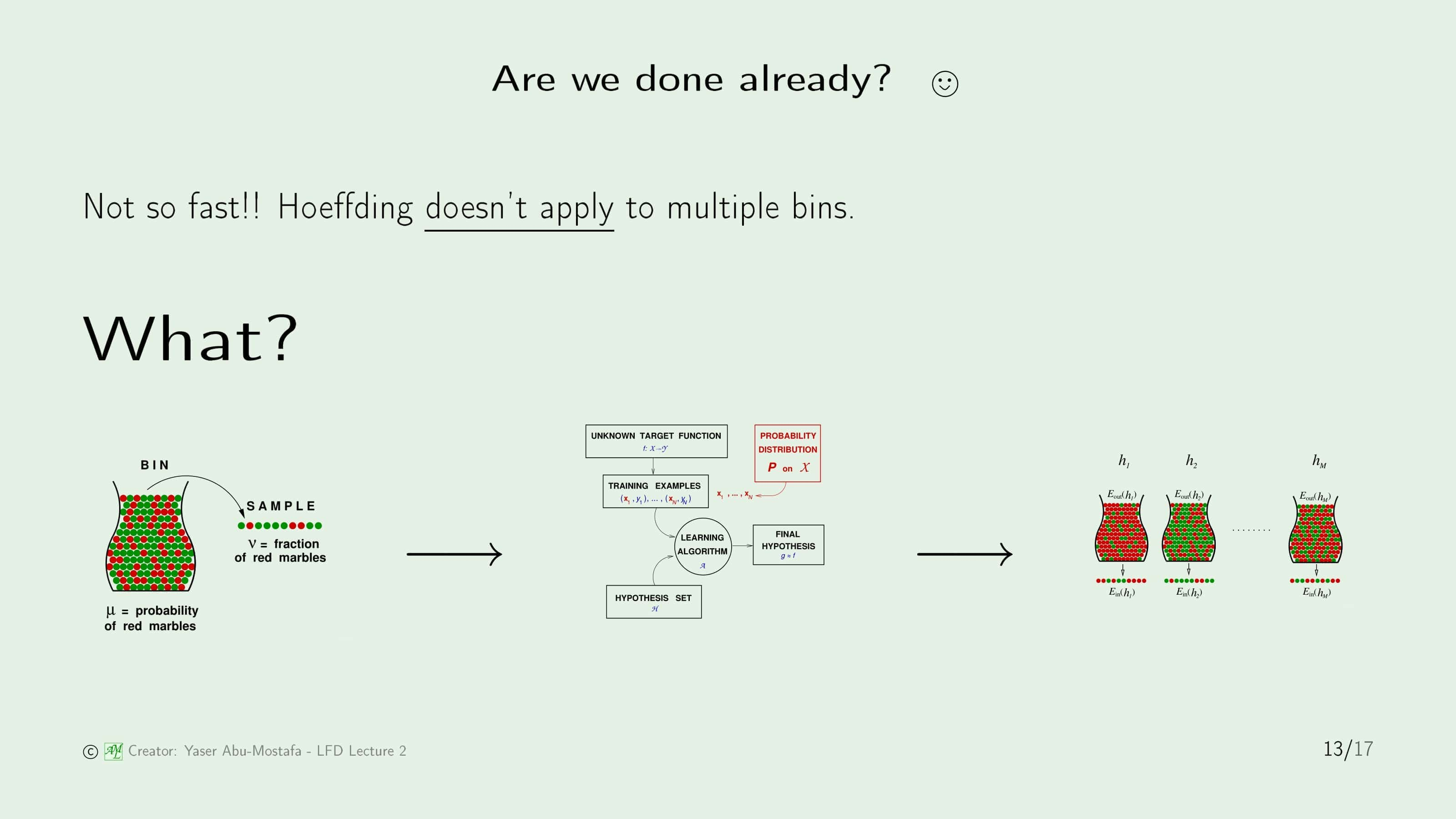
자 그럼 모든 Hypothesis에서 적용되게 만든 것으로 바꾼 것으로 문제가 해결되었을까요? 아니, 근데 더 큰 문제가 생겼습니다. 하나의 Hypothesis 가정을 전체의 Hypothesis 가정으로 바꿨더니 이제는 Hoeffding’s Inequality가 적용되지 않는 문제가 발생했습니다!

왜 Hoeffding’s Inequality가 적용되지 않는지 동전 던지기 예제를 통해 알아봅시다. 만약에 공평한 동전(던졌을 때 앞이 나올 확률과 뒤가 나올 확률이 같은 동전) 한개를 10번 던졌을 때 10번 전부 앞면이 나올 확률은 0.1% 정도 됩니다. 그런데 1000개의 동전을 10번 던졌을 때 10번 전부 앞면이 나오는 동전이 1개 이상 있을 확률이 63%나 됨을 알 수 있습니다. 아까 구슬의 들어있는 통들과 연결이 되시나요?

이 예제에서 동전을 우리가 생각했던 Hypothesis(=구슬이 들어있는 통)로 매칭시킨다면 여러개의 Hypothesis를 사용했을 때에도 확률이 더해짐을 알 수 있습니다. 조금 더 세부적으로, 우리가 직접 확인하는 Sample data (In Sample)도 전체 중에서 무작위로 뽑히므로, 이 중에는 정말 운이 좋게도 모든 Sample이 Hypothesis에 들어맞는 경우(즉, $E_{in} (h) = 0$)도 나올 수 있습니다. 그럼 이게 바로 정답일까요? 하지만 슬프게도 당연히 아니겠죠. 이건 정말 운좋게 Sample이 이렇게 나온 것일 뿐이니까요.

이전의 우리의 문제는 여러개의 Hypothesis를 사용했을 때 Hoeffding’s Inequality가 적용되지 않는 것이였으므로, 방금 전의 동전 예제를 이용해 적용이 되게끔 식을 바꾸어봅시다. 눈썰미가 좋으신 분이면 위 슬라이드 식의 좌항이 $h$에 대한 In Sample/Out of Sample Error가 아니라 $g$에 관한 In Sample/Out of Sample Error로 바뀌었다는 것을 눈치채셨을 겁니다. 여기서의 $g$는 이전 장에서 언급했듯이 Hypothesis set에서 가장 성능이 좋은 Hypothesis를 의미하는 겁니다. 성능이 가장 좋다는 뜻은, ($g$에서 In Sample Error와 Out of Sample Error의 차이가 $\epsilon$보다 클 확률)이 다른 모든 Hypothesis와 비교해 보았을 때, (임의의 $h$에서 In Sample Error와 Out of Sample Error의 차이가 $\epsilon$보다 클 확률) 이하라는 의미입니다.

오른쪽 항에서는 각각의 Hypothesis에 대해서 각각 Hoeffding’s Inequality가 적용되므로, 간단하게 이를 합친다면 각각 Hypothesis에서 발생하는 Hoeffding’s Inequality를 더한 값으로 볼 수 있습니다.

결과적으로 $g$에서의 Hoeffding’s Inequality는 기존의 Hoeffding’s Inequality 좌항에 Hypothesis의 개수인 $M$을 곱한 값이 되었습니다. 이 식은 겉으로 보기엔 아무 문제가 없지만, 오른쪽 항의 $M$이 아주 큰 문제를 야기할 수 있습니다. 아까도 설명드렸다시피 오른쪽 항이 의미가 있으려면 0과 1 사이의 값으로 나와야 하는데, 만약 Hypothesis의 개수(=$M$)가 엄청나게 많다면 1보다 작다는 것을 보장할 수 업습니다. 오른쪽 항이 1보다 크게 된다면 결과적으로 이 식은 아무런 의미를 가질 수가 없습니다. 불행하게도, 일반적인 문제에서 Hypothesis의 개수는 매우 많습니다. 이 부등식을 의미있게 하기 위해서는 좀 더 tight한 범위로 잡을 필요가 있습니다. 궁금하시겠지만, 이 이야기는 5장에서 이어지게 됩니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.