Regularization

12장은 지난 시간에 배웠던 문제점인 Overfitting을 해결하는 방법 중 Regularization (정규화)에 대해 배우게 됩니다.

Outline

이번 장에서는 먼저 직관적인 접근 방식으로 정규화가 무엇인지 알아보고, 그 후에 수학적인 방법으로 정규화가 정확하게 무엇인지 알아봅니다. 그 후 정규화에서 중요한 Weight Decay가 무엇인지 배운 다음, Regularizer를 선택하는 방법을 공부하게 됩니다.

Regularization - informal

정규화에 접근하는 방식은 두 가지 방법이 있습니다. 먼저 수학적으로 문제점을 분석해 해결하는 방법을 유도하는 방법이 있고, 다른 방법으로는 단지 $E_{in}$을 최소화하는 것을 방해하는 요소가 무엇이었는지를 따져가며 해결하는 방법을 찾는 방법입니다. 여기서는 두 번째 방법을 먼저 사용한다고 합니다.

이 예제는 8장에서 사용했던 예제입니다. Target Function이 $y=\sin(\pi x)$이고 가설 모델이 1차 함수인 상황에서 무작위로 2개의 데이터가 주어졌을 때 발생하는 가설을 그린 것입니다. 이 당시에는 Variance가 너무 컸기 때문에 상수 함수보다 나쁜 가설 모델임을 밝혔습니다. 그런데 오른쪽 그림처럼 이 가설 모델에 정규화를 도입하고 나니 가설들이 발생 분포가 조금 작아진 것처럼 보입니다. 여기서는 가설의 기울기에 제한을 두어 기울기가 너무 가파른 직선은 가설에서 제외하는 방법을 사용하였다고 합니다.

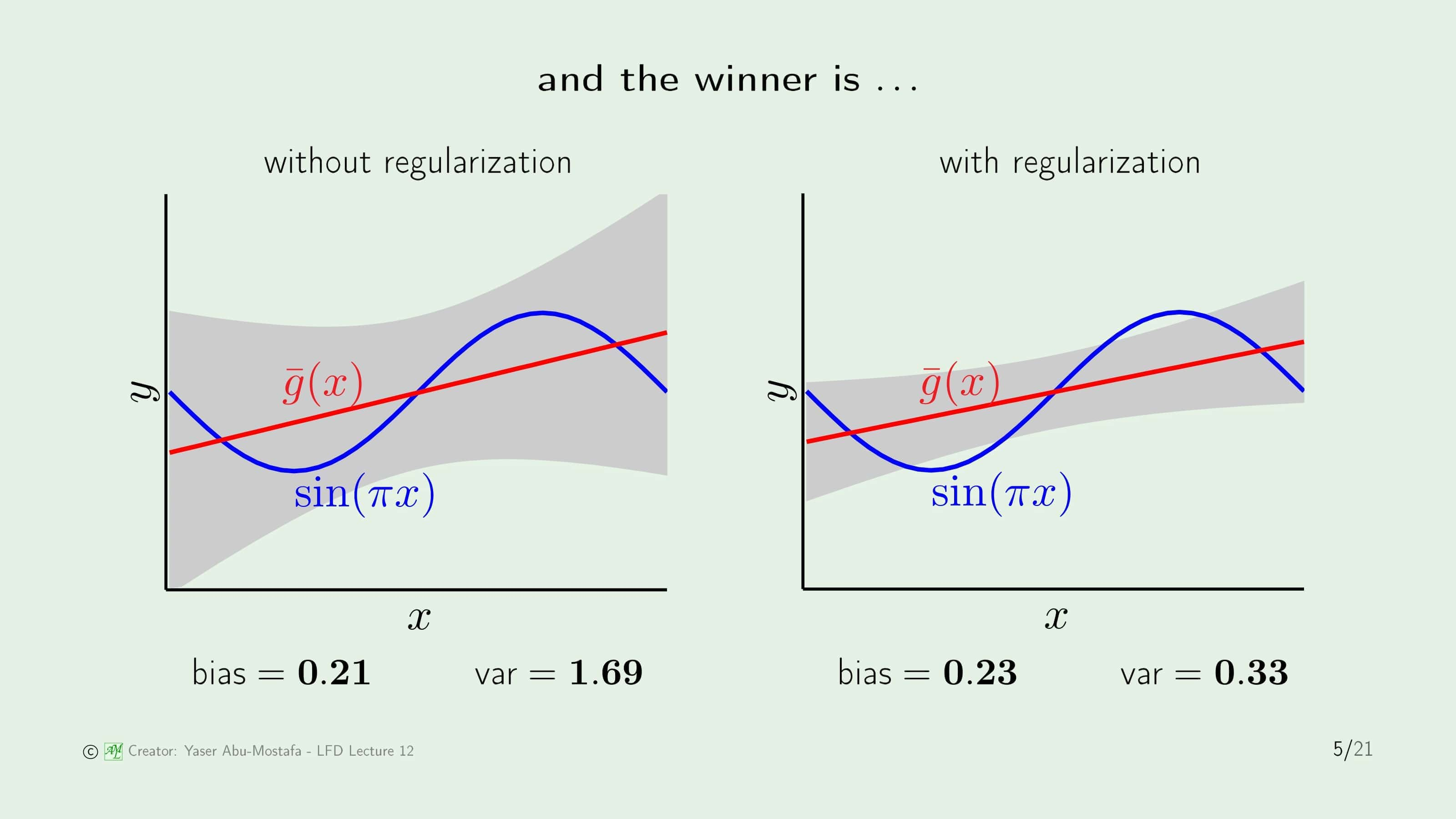
예상대로 정규화를 거친 경우 그렇지 않은 경우에 비해 성능이 좋아진 것을 볼 수 있습니다. 빨간색 선의 위치는 동일한 것처럼 보이지만, 실제로는 모델의 분포가 줄어들었기 때문에 살짝 틀어져 Bias는 약간 높게 나오지만, Target Function의 범위를 초과하는 영역은 모두 사라졌기 때문에 Variance는 급격하게 줄어들었습니다.

Regularization - formal

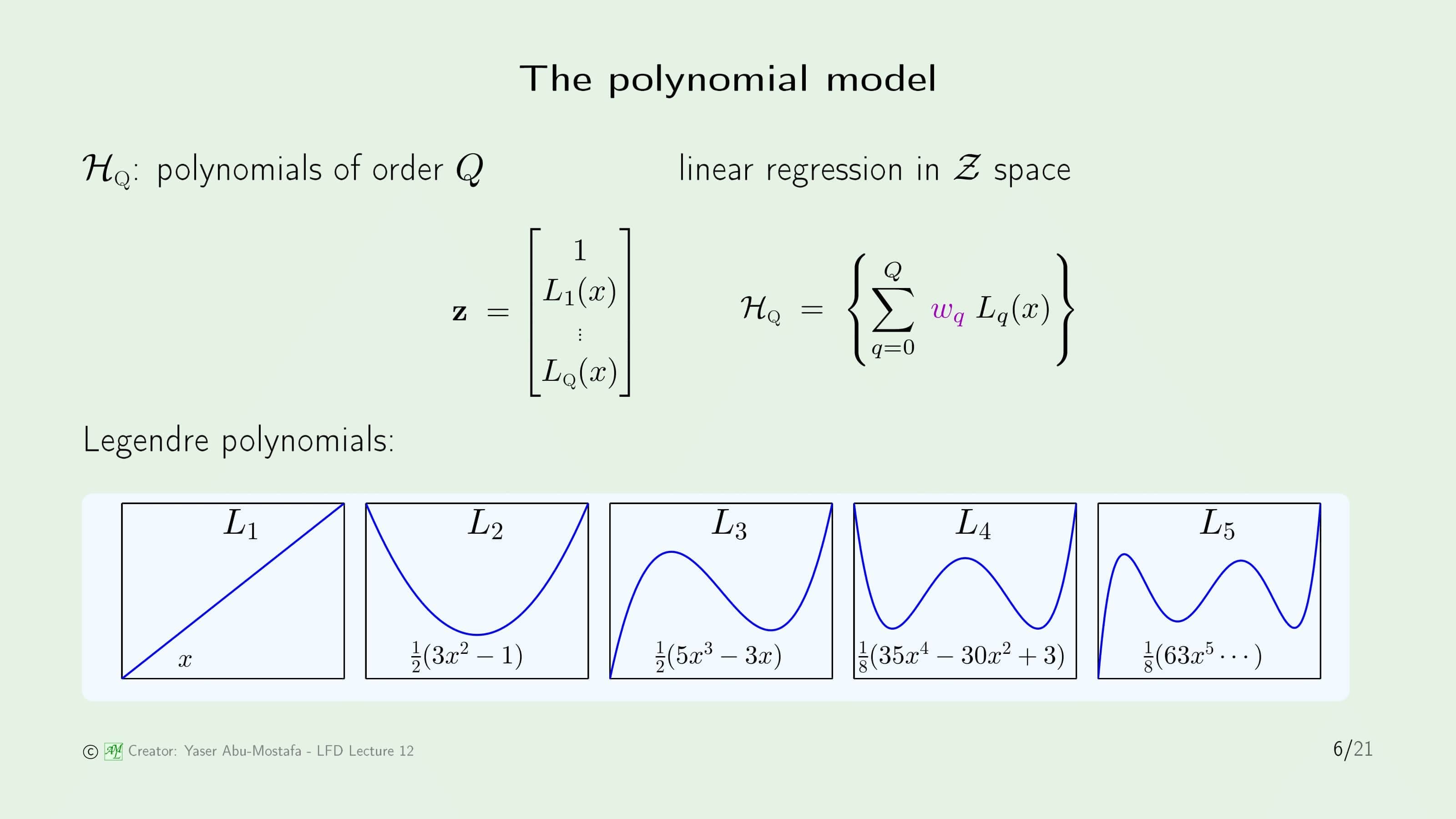
이제 이런 정규화를 수학적으로 유도해볼 차례입니다. 이번에도 예를 들어 설명할텐데, 조금 복잡한 방법으로 Legendre Polynomials (르장드르 다항식)을 사용한 Transform을 예제로 다루게 됩니다.

Legendre Polynomial은 Legendre Differential Equation (르장드르 미분 방정식)의 해가 되는 함수들을 일컫는데, 여기서는 구체적으로 Legendre Polynomial이 무엇인가까지 알 필요는 없습니다.

다만 Legendre Polynomial은 최고차항이 1, 2, 3, … 일 때 각각 고유한 함수를 갖는데, 그 고유한 함수를 각각 $L_1, L_2, L_3, …$로 정의합니다. 위의 슬라이드에서는 $L_1$부터 $L_5$까지의 르장드르 다항식이 어떤 함수인지를 나타내고 있습니다.

가설 모델 $\mathcal{H}_Q$는 최고차항이 $Q$인 다항식이라 가정합니다. 비선형 변환 $\mathbf{z}$는 1(=$L_0$)부터 $L_Q$까지를 원소로 갖는 벡터입니다. 이것을 사용하여 구체적인 $\mathcal{H}_Q$를 유도하면 각 Legendre Polynomial에 Weight $w_q$를 곱한 후 더한 형태로 만들 수 있습니다.

그렇다면 주어진 데이터 $(x_1, y_1), … ,(x_N, y_n)$을 Transform을 통해 $(\mathbf{z}_1, y_1),$ $…, (\mathbf{z}_N, y_n)$를 만들면 $\mathbf{z}$에 대한 새로운 In Sample Error $E_{in}$을 유도할 수 있습니다. 이후의 전개는 3장에서 배운 Pseudo Inverse (유사 역행렬)을 구하시면 됩니다.

즉, 임의의 일반적인 데이터 $\mathbf{x}$가 주어진다면, 이를 Legendre Polynomial을 벡터로 갖는 $\mathbf{z}$로 Transform을 하고 Pseudo Inverse를 통해 가중치 벡터 $\mathbf{w}$를 구할 수 있습니다.

만약에 가중치 벡터가 제한된 상황에서는 어떻게 변하는지 알아봅시다. 지난 시간에 가설 모델 중 2차 방정식 모델 $\mathcal{H}_2$와 10차 방정식 모델 $\mathcal{H}_{10}$을 비교하였습니다. 그런데 생각해보면, $\mathcal{H}_2$는 $\mathcal{H}_{10}$의 제한된 버전, 즉 3차 이상의 항의 계수를 0으로 한 모델임을 알 수 있습니다.

이 것과 비슷하게 각 가중치를 제곱한 합을 일정 값 $C$ 이하로 제한하는 방법을 생각해볼 수 있습니다. 제곱이 되는 이유는 In Sample Error를 계산하는 식에 가중치 벡터 $\mathbf{w}$의 제곱이 들어가기 때문입니다. 이 제한이 들어갔을 때 나오는 해답을 이전의 해답과 비교하기 위해 $\mathbf{w}_{reg}$라고 정의합니다.

제한 조건이 없는 In Sample Error $E_{in}$을 상수값과 같다고 식을 놓고 2차원으로 표현하면 오른쪽과 같은 파란색 타원으로 표현할 수 있습니다. 원의 중심으로 갈수록 $E_{in}$의 값이 낮아지기 때문에 제한조건이 없을 때의 해답 $\mathbf{w}_{lin}$은 원의 중심이 됩니다. 마찬가지로 제한 조건만을 2차원으로 표현한다면 빨간색 원으로 그릴 수 있습니다. 제한조건을 만족하면서 $E_{in}$을 최소화하는 점은 파란색 타원과 빨간색 원이 겹치는 영역에 포함됨을 알 수 있습니다.

$E_{in}$을 최소로 만드는 점을 찾기 전에, 영역에 포함되는 점 중 하나인 $\mathbf{w}$를 하나 가정해봅시다. 이 점에서의 기울기(Gradient)를 구하게 되면 파란색 원의 바깥쪽을 향하게 됩니다. (경사하강법에서 목적지에 도달하기 위해 기울기의 반대 방향으로 갔던 것을 떠올리면 됩니다) 그리고 빨간색 원을 기준으로 $\mathbf{w}$에서 법선 벡터(Normal Vector)를 구하게 되면 역시 원 바깥으로 향하는 벡터가 생성됨을 쉽게 알 수 있습니다. 그렇다면 여기서 $E_{in}$을 최소화하려면 $\mathbf{w}$를 어느 방향으로 움직여야 할까요? 당연히 빨간색 원을 따라 움직여서 $\mathbf{w}_{lin}$에 최대한 가까운 점으로 움직이면 될 것입니다. 그 방향을 $\mathbf{w}$를 기준으로 표현한다면, $E_{in}$ 기울기의 반대 방향과 제한조건의 법선벡터 반대 방향으로 움직여야 함을 알 수 있습니다.

이를 수학적으로 표현하면 $E_{in}$의 변화량 $\nabla E_{in}(\mathbf{w}_{reg})$은 $-\mathbf{w}_{reg}$에 비례한다고 말할 수 있습니다. 정확한 값으로는 $-2 \times \frac{\lambda}{N}\mathbf{w}_{reg}$로 표현하는데, 왜 갑자기 이 식이 나왔는지는 강의를 들어도 잘 이해가 되지 않습니다. 알게 되면 글을 수정하겠습니다. 혹시 아시는 분은 댓글로 알려주시면 감사하겠습니다.

어쨌든 $\nabla E_{in}(\mathbf{w}_{reg})$의 오른쪽 항을 이항하면 오른쪽 항에는 0벡터만 남게 됩니다. 그런데 이 식은 어떤 식을 미분한 식처럼 보입니다. 쉽게 말해, $E_{in}(\mathbf{w}) + \frac{\lambda}{N}\mathbf{w}^{\sf T}\mathbf{w}$을 최소화하기 위하여 이를 미분했을 때의 결과로 보입니다.

여기서 문제는 제한이 들어갔을 때의 상수 $C$가 이 식에는 사라져 있다는 것입니다. 대신 다른 상수 $\lambda$가 존재합니다. 다행히도 이 두 상수간에는 관계가 존재하는데, $C$가 증가할수록 $\lambda$가 줄어든다는 것이고 그 반대도 성립한다는 겁니다. 즉, 우리가 $C$의 값을 조절하고 싶다면 그 대신 $\lambda$를 조절함으로써 동일한 결과를 얻을 수 있다는 것입니다.

이번에는 Augmented Error가 무엇인지 살펴보겠습니다. 이전 슬라이드에서 유도한 $E_{in}(\mathbf{w}) + \frac{\lambda}{N}\mathbf{w}^{\sf T}\mathbf{w}$식을 간단하게 $E_{aug}(\mathbf{w})$로 정의합니다. 여기서 $E_{in}$을 우리가 아는 식으로 대입하고, 그 식을 정리하면 이전 슬라이드에서 처음 시작했던 식과 동일한 결과가 나옵니다. (전개 과정은 추후에 글을 수정함으로써 보충하도록 하겠습니다)

이 식은 가설 집합을 명시적으로 제한하고 있기 때문에 7장에서 배웠던 VC Analysis에 적합하다고 합니다.

이전 슬라이드에서 정의했던 $E_{aug}(\mathbf{w})$을 최소화하는 계산을 시도해봅시다. 식을 정리하여 미분값이 0이 되는 점을 찾으려면 $Z^{\sf T}(Z\mathbf{w}-\mathbf{y})+\lambda\mathbf{w})=\mathbf{0}$을 계산하면 됩니다. 이를 정리하여 $\mathbf{w}$를 계산하면 $(Z^{\sf T}Z + \lambda\mathbf{I})^{-1}Z^{\sf T}\mathbf{y}$을 됩니다. 정규화를 적용하기 전에 구했던 $\mathbf{w}_{lin}$과는 $\lambda\mathbf{I}$ 만큼의 차이가 있다는 것이 쉽게 보입니다.

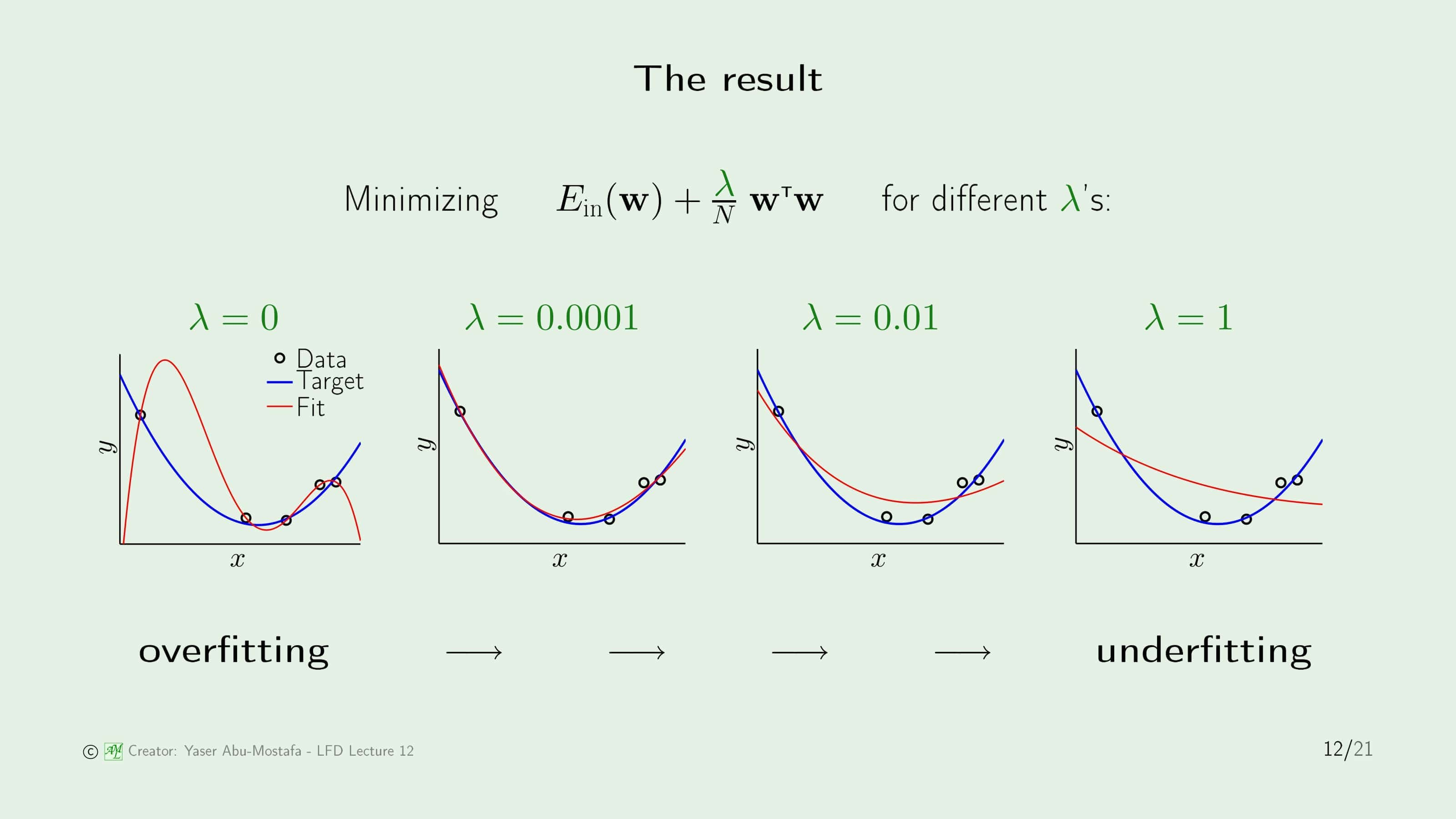
그렇다면 이번에는 $\lambda$의 값을 변화시킴으로써 학습 결과가 어떻게 변하는 지 알아보겠습니다. $\lambda=0$일 때는 정규화를 사용하지 않는 것과 같으므로 Overfitting이 일어납니다. 그런데 $\lambda$를 0.0001로 아주 약간만 올리게 되면 Target Function과 거의 비슷한 결과가 나오게 됩니다. $\lambda$를 조금 더 증가시켜 0.01로 설정하면 오히려 이전보다 Target Function과 더 멀어지지만, 그래도 Overfitting이 일어났을 때보다는 결과가 좋습니다. $\lambda$를 1까지 증가시키게 되면 오히려 학습을 제대로 하지 못하는 Underfitting이 일어나버립니다. $\lambda$가 커질수록 학습 결과는 점점 더 평평해지고, 너무 크게 정한다면 Underfitting이라는 새로운 문제가 생기기 때문에 적절한 $\lambda$의 값을 찾는 것이 중요하지만, 안타깝게도 최선의 $\lambda$를 찾을 수 있는 방법이 존재하지 않기 때문에 아주 작은 값부터 값을 올려가며 $\lambda$을 찾는 경험적인 방법을 사용할 수밖에 없습니다.

Weight decay

지금까지 설명했던 방법을 Weight Decay라고 부릅니다. 왜 그런지 이유를 알아보기 위해 인공신경망 모델에서 경사하강법을 사용하는 상황을 가정해봅시다. 원래의 경사하강법의 수식에서 정규화를 적용한다면 $-2\eta\frac{\lambda}{N}\mathbf{w}(t)$ 항이 추가됩니다. 이 항이 포함된 식을 정리한다면 $\mathbf{w}(t)$가 $(1-2\eta\frac{\lambda}{N})$ 로 묶이게 됩니다. 즉, $t$가 한 단계 증가할 때마다 $\mathbf{w}(t)$는 조금씩 작아지게 됩니다. 이것이 바로 Weight Decay라고 불리게 되는 이유입니다.

Weight Decay의 변형에는 어떤 것들이 있는지 알아보겠습니다. 가중치 벡터의 각 Element $w_q^2$를 제곱한 값에 $\gamma_q$를 곱해준 것을 Regularizer라고 가정해봅시다. 여기서 $\gamma_q$를 어떻게 정하느냐에 따라 가중치 벡터의 Element의 크기를 정해줄 수 있습니다. 시그마 수식의 전체 총합은 일정한 상수 $C$ 보다 작아야 하기 때문인데요, 만약에 $\gamma_q$가 크다면 제한 사항을 만족해야 하기 때문에 가중치 벡터의 Element들은 크기가 작을 수밖에 없고, 반대로 $\gamma_q$가 작다면 Element를 그보다 크게 정할 수 있기 때문입니다.

여기에서는 두 가지 반대 케이스를 보여주는데, $\gamma_q=2^q$인 경우에는 함수의 차수를 작게 맞추려고 합니다. 예를 들어 가설 모델이 고차 다항식인 경우에는 낮은 차수의 다항식과 맞추려는 역할을 하게 된다는 뜻입니다. 반대로 $\gamma_q=2^{-q}$인 경우라면 좀 더 고차인 다항식에 맞추려고 하기 때문에 Target Function이 복잡한 함수로 예상되는 경우에 좋은 퍼포먼스를 보일 수 있을 것입니다.

인공신경망에서는 각 레이어마다 다른 $\gamma$의 값을 정해준다고 합니다. 가장 유명한 식은 Tikhonov Regularizer라는 것인데, 처음 주어졌던 식과는 다르게 완전한 2차식으로 표현됩니다. 그냥 이런 것이 있구나 정도만 이해하시면 되겠습니다.

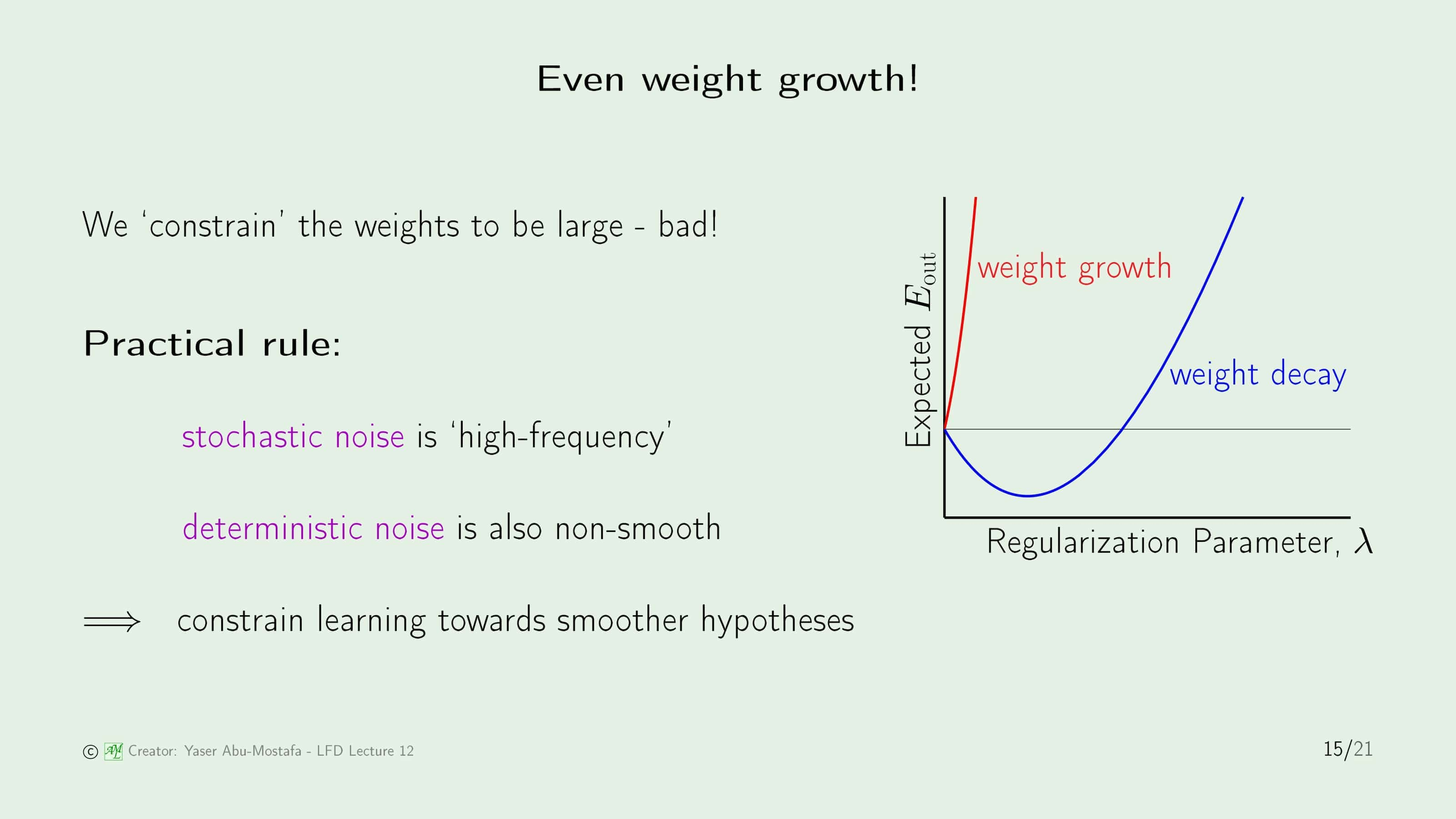
Weight Decay를 배웠으니 그 반대의 경우도 떠올려볼 수 있습니다. 만약에 Weight를 반대로 크게 만든다면 어떻게 될까요?

우선 Weight Decay의 효과를 알기 위해 오른쪽 그림처럼 $\lambda$의 크기를 증가시킬 때 예상되는 Out of Sampel Error $E_{out}$이 어떻게 변하는지 보면, 일정 지점까지는 $\lambda$를 증가시킬 때 $E_{out}$이 감소하지만, 그 이후부터는 오히려 증가함을 알 수 있습니다. 만약에 Weight growth를 시키는 상황에서 $\lambda$를 증가시킨다면? 그냥 $E_{out}$이 바로 수직 상승해 버립니다. 이렇게 되면 Weight Growth를 하게 되면 엄청나게 큰 문제가 생길 것 같지만, 실제로 계산을 해보면 Weight Growth에서는 $\lambda$를 0으로 유도하기 때문에 계산의 낭비만을 제외하고는 정규화를 사용하지 않는 것과 차이는 없다고 합니다.

또한 여기서 실용적인 규칙을 하나 알려주는데, Stochastic Noise는 High-frequency이고 Deterministic Noise는 Non-smooth라고 합니다. (강의에서 정말 간단하게 알려주고 넘어가는데, 저는 강의만 보고서는 이게 무슨 의미인지는 알지 못하겠습니다. 혹시라도 아시는 분은 댓글로 부탁드립니다.) Regularize는 더 Smooth 한 가설을 선택하는 경향이 있다고 합니다.

Weight Decay의 Regularizer를 $\Omega$라고 정의해 봅시다. $E_{aug}$는 $\Omega$의 형태로 표현할 수 있습니다. 여기서 $h$는 $\mathbf{w}$에 영향을 주는 변수라고 생각하시면 됩니다. 그런데 이 식을 조금만 변형시키면, 7장에서 보았던 Generalization Bound와 유사함을 알 수 있습니다. 물론 이 때는 $E_{aug}$가 아니라 $E_{out}$이었습니다. 그다음 문장이 조금 이해하기 어려운데, $E_{aug}$는 $E_{out}$에 대한 대용물로써 $E_{in}$보다 낫다고 합니다. 그 이유를 인터넷 강의에서 자세하게 설명해주지 않아서 이 부분은 추후에 공부한 후 보강하겠습니다.

Choosing a regularizer

그렇다면 문제별로 어떻게 빠르게 Regularizer를 선택하는지 그 방법을 알아보도록 하겠습니다.

완벽한 Regularizer가 무엇일까요? Target Function은 알 수 없지만 그 방향으로 갈 수 있게 만드는, 즉 Target Function과 최대한 가까워질 수 있게 만드는 Regularizer일 것입니다. Regularization은 기본적으로 Overfitting을 완화시키는 목적으로 사용되기에, Noise를 손상시키게 됩니다. Perfect Regularizer는 Closed Form을 구하는 것이 아닌, 경험적인 방법으로 유도하게 됩니다. 여기에서는 가이드라인으로 Smooth 하거나 간단한 방향으로 움직여야 한다고 말합니다. 그 이유는 Noise가 Smooth 하지 않기 때문입니다. 그 방향으로 가게 되면 Noise를 더 손상시킬 수 있다고 합니다.

만약에 나쁜 $\Omega$를 선택한다면 어떻게 될까요? 다행히도 $\lambda$의 값을 잘 조절한다면 나쁜 $\Omega$를 선택한다고 해도 Overfitting을 해결할 수 있다고 합니다.

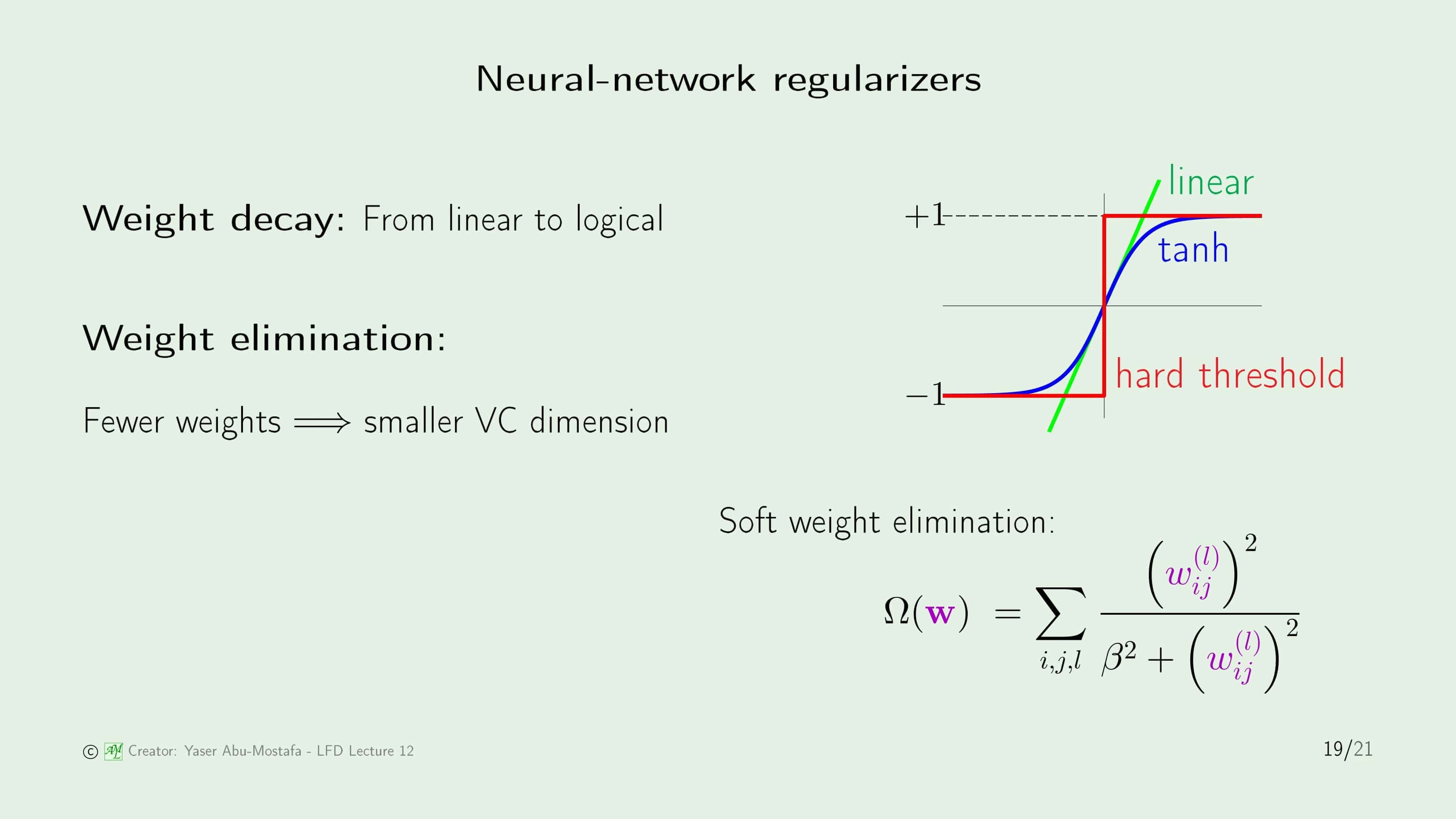
이번에는 특별한 예제로 인공신경망 모델에서의 Regularizer를 직관적으로 선택해보겠습니다. 인공신경망 모델에서 큰 가중치와 작은 가중치를 사용하는 경우를 각각 따져봅시다. 만약에 매우 작은 가중치를 선택한다면, 가중치는 원점 근처, 즉 Linear 함수와 다르지 않은 부분에 분포해 있을 것입니다. 결과적으로 매우 작은 가중치에서는 간단한 선형 함수를 구현하는 것입니다. 반대로 가중치가 큰 경우라면 선형 부분을 넘어 Logical 한 부분으로 가게 됩니다.

인공신경망에서는 Overfitting을 해결하는 방법 중 하나로 Weight Elimination이 있습니다. 이름 그대로 몇 개의 Weight를 아예 0으로 만들어 버리는 방법입니다. Weight의 수가 적어진다면 그만큼 VC Dimension이 줄어들기 때문입니다. 다만 여기서는 완전히 0으로 만들어버리기보다는 Soft 한 방법을 제시하고 있는데, $\gamma$를 $\frac{\beta^2}{(w_{ij}^{(l)})^2}$로 정의하는 것입니다. 이렇게 되면 $w$가 작은 경우에는 $\frac{1}{\beta^2}$에 가깝게 될 것이고 $w$가 큰 경우라면 1에 가깝게 될 것입니다. 결과적으로 덜 중요한 Weight들은 0에 가깝게 되지만 중요한 Weight들은 그 값이 그대로 유지되게 됩니다.

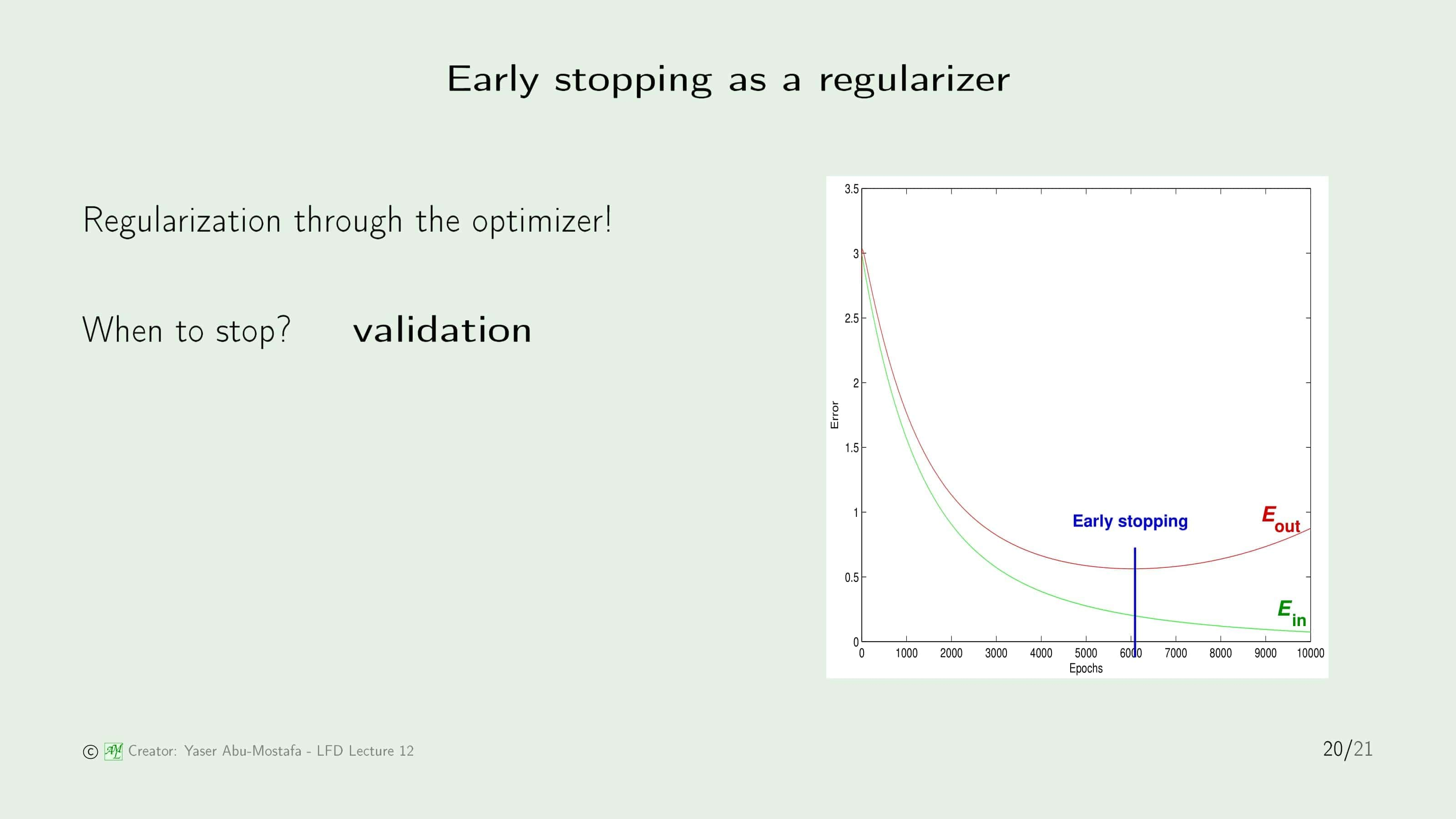
지난 장에서 살짝 언급하였던 Early Stopping 또한 Regularizer의 한 형태입니다. 이 방법은 특이하게 목적 함수를 변화시키지 않습니다. 학습을 언제 멈춰야 할지를 선택하는 방식이기 때문입니다. 이런 해결 방법을 Validation이라고 부르는데, 이것은 다음 장에서 더 자세하게 다루도록 하겠습니다.

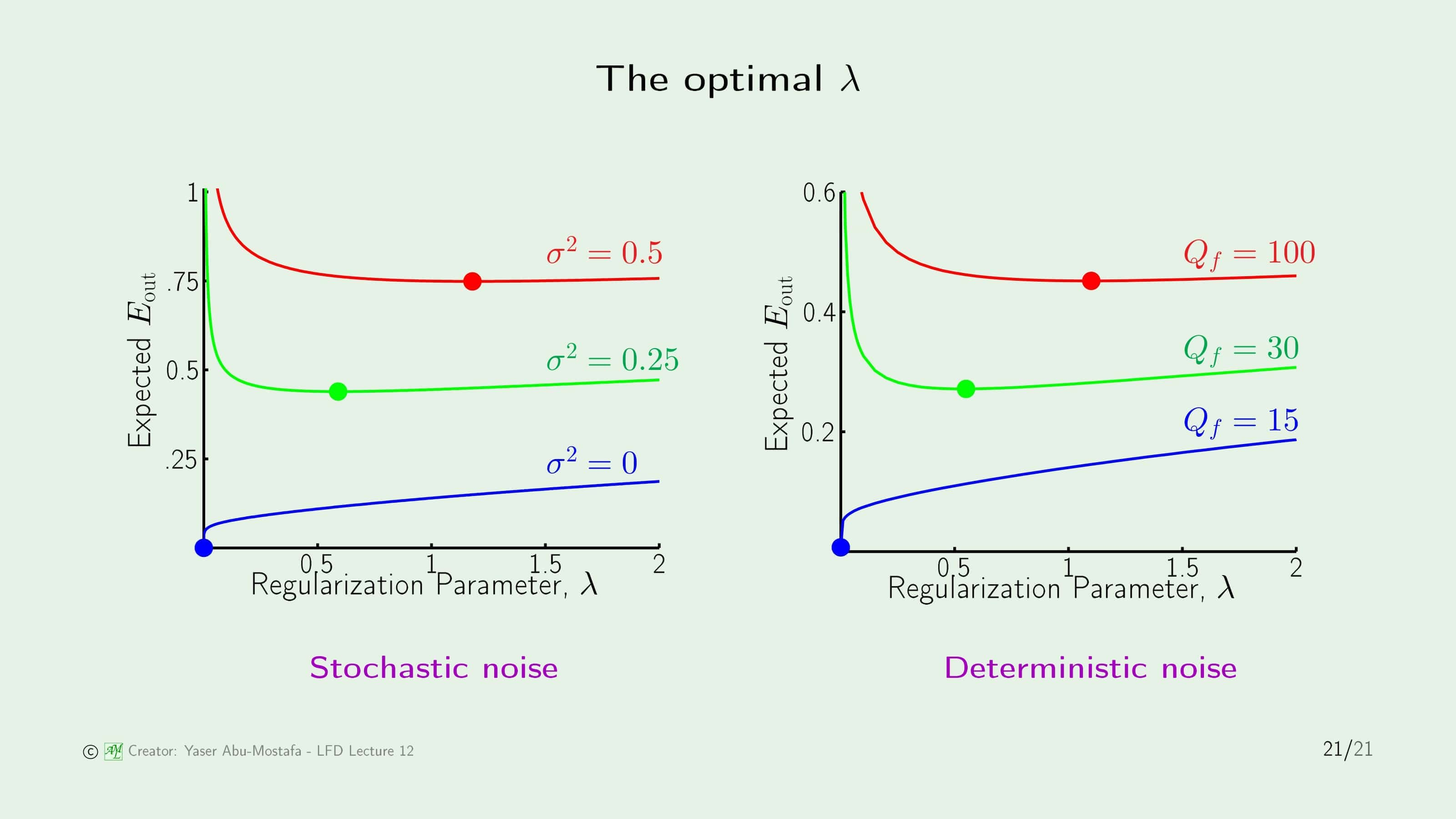
이제는 최적의 $\lambda$를 찾는 방법을 알아봅시다. 왼쪽의 그래프는 Stocahstic Noise가 정규분포를 따른다고 가정했을 때 Variation 별 $\lambda$와 예상되는 Out of Sample Error를 나타낸 것입니다. 만약에 Variation이 0이라면(=Stochastic Noise가 없다면) 정규화 자체를 할 필요가 없음을 알 수 있습니다. Variation이 0.25일 때와 0.5일 때를 비교하면 Variation이 클수록 $\lambda$의 값 또한 커져야 함이 보입니다.

오른쪽 그래프는 Deterministic Noise인 Target Function의 차수에 따른 $\lambda$와 Out of Sample Error의 상관관계를 나타내고 있습니다. 이 역시 Stochastic Noise 때와 비슷하게, 차수가 높을수록 높은 $\lambda$값으로 정해야 함을 알 수 있습니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.