Support Vector Machines

14장은 새로운 기계학습의 방법인 Support Vector Machine을 배우게 됩니다. 지금처럼 Neural Network가 유명해지기 전까지는 가장 널리 쓰이던 방법이었습니다.

Outline

이번 장은 Classification 문제에서 Margin을 최대화하는 것부터 시작해서, 그것을 찾는 해법, 그리고 Nonlinear Transform에 응용하는 방법까지를 다루게 됩니다.

Maximizing the margin

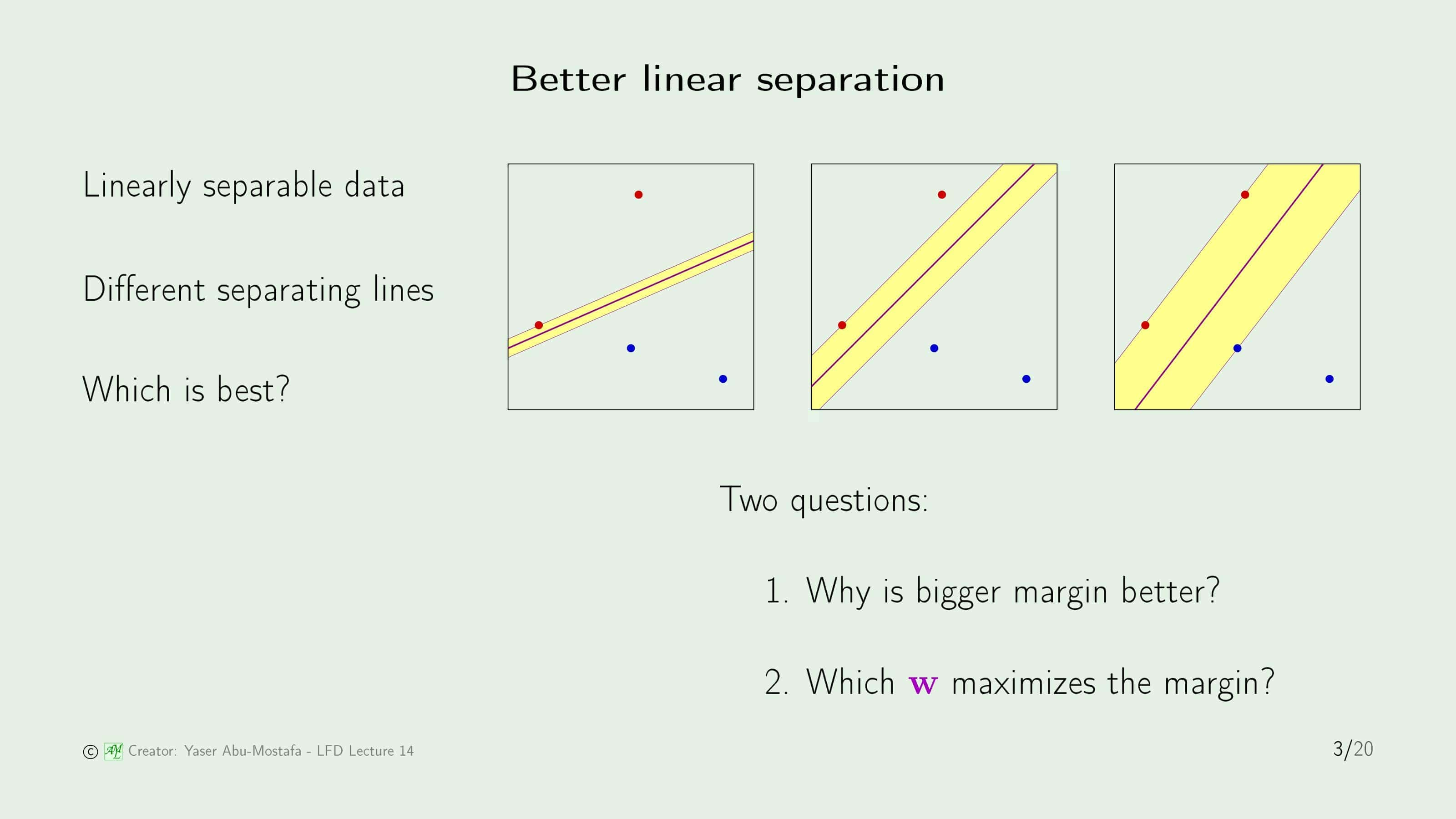
먼저, 선형 분리가 가능한 데이터 집합이 있다고 가정해봅시다. 간단하게 표현하기 위해, 상단의 그림처럼 4개의 데이터만 존재하고, 빨간색과 파란색으로 분류하는 문제를 예로 들어보겠습니다. 이 문제를 해결하기 위해 두 데이터 종류를 분리하는 선을 그어야 하는데, 빨간색과 파란색을 분리하기만 하면 되므로 해답은 무수히 많습니다. 슬라이드에는 그 중 3가지의 해답을 보여주고 있습니다.

위의 그림에 나온 분리선을 위 아래로 평행이동시킨다고 가정해봅시다. 어느 방향으로 움직이든 처음으로 데이터를 만나는 곳까지를 Margin으로 정의합니다. Margin의 의미는 데이터 분리에 오류가 발생하기 전까지 움직일 수 있는 영역을 의미합니다. 이를 3개의 그림에서 노란색 영역으로 표시한 것을 알 수 있습니다.

세 그림에서 분리선은 모두 주어진 데이터를 올바르게 나누고 있습니다. 하지만 만약에 이 중 하나를 고르라고 하면 많은 분들이 3번째 그림을 고를 것입니다. 왜냐하면 3번째 그림의 Margin이 가장 크다는 것을 알기 때문입니다. 여기서 두 가지 의문이 생깁니다.

1. 왜 Margin이 클 수록 좋은가?
2. Margin을 크게 만들기 위해서 $\mathbf{w}$를 어떻게 설정해야 하는가?

첫 번째 의문에 대한 답은 Margin이 크다면 데이터에 Noise가 있는 경우 Error를 일으킬 확률이 줄어들기 때문입니다. 첫 번째와 같이 나누게 되면, 빨간 점의 노이즈로 인해 분리선을 넘는 데이터가 발생할 확률이 상당히 높게 발생할 수 있습니다. 그에 반해 세 번째 그림의 분리선은, 데이터와 멀리 떨어져 있기 때문에 그럴 위험이 상대적으로 적음을 쉽게 알 수 있습니다.

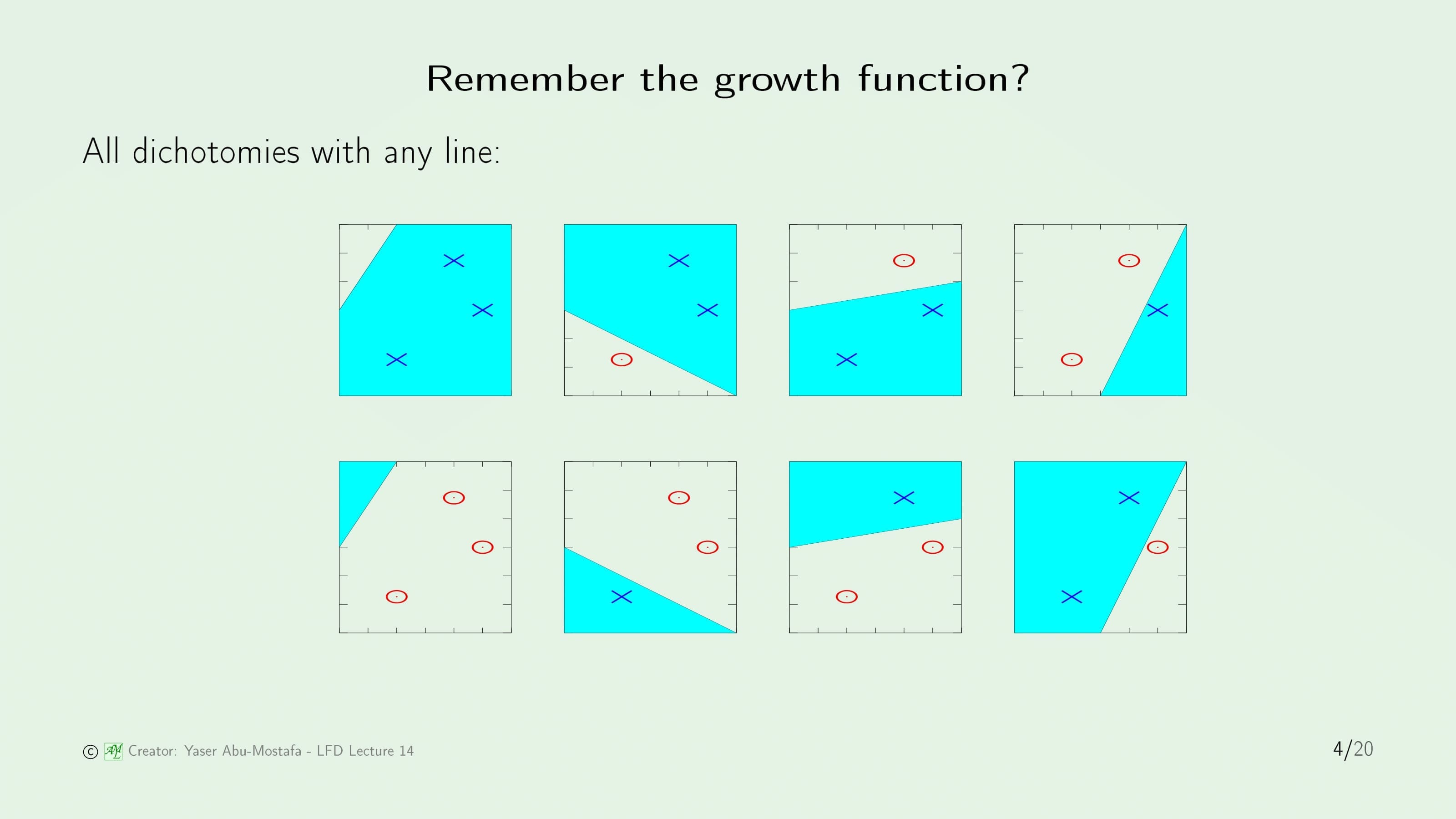
잠시 5장에서 배운 Growth Function을 떠올려봅시다. 만약에 데이터가 3개이고, 선으로 데이터를 나누는 예제가 있다고 가정합니다. 이 예제에서는 3개의 점으로 가능한 모든 경우인 $2^3=8$개의 경우의 수가 나왔습니다. 이 말은 Growth Function이 크다는 것이고, Growth Function이 크다는 것은 일반화가 쉽지 않다는 말과 같습니다.

일반화 문제를 해결하기 위해서, 먼저 똑같은 예제에서 8개의 경우를 각각 Margin이 가장 큰 방법으로 나누어보겠습니다. 데이터가 무작위로 분포해있기 때문에, 그림을 보시면 아시겠지만 나누었을 때 Margin이 큰 경우도 있고, 작은 경우도 있습니다. 만약에 우리가 Margin이 Fat한 경우만 허용한다면, 위의 3번째 그림과 같은 경우는 사용할 수 없으므로, 경우의 수가 줄어들게 됩니다. 즉, Fat Margin은 Dichotomy의 수를 줄인다라는 것을 의미합니다.

그렇다면 이제는 선형 분류에서, 두 종류의 데이터를 나누는 작업에 Margin이 커야 한다는 조건이 추가된 것입니다. 그렇게 만들기 위해 $\mathbf{w}$를 어떻게 찾아야하는지를 알아보겠습니다.

Margin은 단순하게 나누는 평면에서 데이터 점까지의 거리입니다. 그 거리를 계산하기 위해, 먼저 데이터를 나누는 평면 $\mathbf{w}^{\sf T} \mathbf{x} = 0$ 과 가장 가까운 점 $\mathbf{x}_n$를 가정합니다. 데이터를 나누는 것을 선이 아니라 평면이라고 지칭하는 이유는 2차원이 아닌 일반적인 차원을 기준으로 계산해야하기 때문입니다.

그렇다면 이제는 평면과 점 사이의 거리를 계산해야 합니다. 그 전에 먼저 알아야 할 것은 첫째로 $\mathbf{w}$를 정규화하는 것입니다.

둘째로 $w_0$를 식에서 따로 분리하는 것입니다. 기존의 선형 분류에서 $w_0$는 Threshold를 위해 만든 가중치였습니다. 그렇기 때문에 $w_0$의 역할은 $w_1 ~ w_d$까지의 역할과 완전히 다른 역할을 하므로 $\mathbf{w}$에서 따로 분리하는 것이 추후 계산에서 좀 더 편합니다. 이제 $\mathbf{w}$는 $w_1 ~ w_d$으로만 이루어진 벡터라고 가정하고, $w_0$는 $b$로 바꾸어서 더해줄 것입니다. 즉, 이제 평면의 방정식은 $\mathbf{w}^{\sf T} \mathbf{w} + b = 0$으로 바뀐 것입니다.

이제 점 $\mathbf{x}_n$과 평면 $\mathbf{w}^{\sf T} \mathbf{x} + b = 0$ 사이의 거리를 구하는 문제를 해결해야 합니다. $w_0$이 $b$로 바뀌고 $\mathbf{w}$ 밖으로 나왔기 때문에, 1로 정규화시킨 식 또한 약간 바뀐 것을 알 수 있습니다.

이해를 돕기 위해 위 슬라이드의 오른쪽 그림을 참고하면서 계산해봅시다. 고등학교 때 배운 평면의 방정식을 떠올려보면, $\mathbf{w}$는 평면의 법선벡터이기 때문에 평면과 직교하게 됩니다. 이를 보이려면 평면의 임의의 점 $\mathbf{x}^{\prime}$과 $\mathbf{x}^{\prime\prime}$을 잡습니다. 두 점은 평면 위의 점이기 때문에, 평면의 방정식에 대입해도 식이 변하지 않습니다. 식 $\mathbf{w}^{\sf T} \mathbf{x}^{\prime} + b = 0$에서 식 $\mathbf{w}^{\sf T} \mathbf{x}^{\prime} + b = 0$를 뺀다면 $\mathbf{w}^{\sf T} (\mathbf{x}^{\prime} - \mathbf{x}^{\prime\prime})$ 이 됩니다. $\mathbf{w}$와 $(\mathbf{x}^{\prime} - \mathbf{x}^{\prime\prime})$ 두 벡터의 내적이 0이 나오므로, 두 벡터는 직교하는 것이고 $\mathbf{x}^{\prime}$과 $\mathbf{x}^{\prime\prime}$는 평면 위의 임의의 점이므로, 평면과 $\mathbf{w}$는 직교한다고 볼 수 있습니다.

이제 평면 밖의 점 $\mathbf{x}_n$과 평면 사이의 거리를 계산해봅시다. 평면위에 임의의 점 $\mathbf{x}$를 잡고, 벡터 $\mathbf{x}_n - \mathbf{x}$를 $\mathbf{w}$에 사영(Projection)합니다. 이 길이를 구하기 위해, 먼저 $\mathbf{w}$의 단위벡터를 $\hat{\mathbf{w}}$로 정의합니다. 그렇다면 구하려는 거리는 $\hat{\mathbf{w}}^{\sf T} (\mathbf{x}_n - \mathbf{x})$ 벡터의 크기가 됩니다.

이 식에서 단위벡터를 풀고 정리하면, $b$를 한번 더해주고 빼주는 테크닉을 통해 평면의 방정식과 비슷한 형태로 정리할 수 있습니다. 여기서 $\mathbf{w}^{\sf T} \mathbf{x} + b$는 평면의 방정식 정의로 인해 0이고, $\mathbf{w}^{\sf T} \mathbf{x}_n + b$는 1로 정규화를 시켰었기 때문에, 결국 구하려는 거리를 표현한 식은 $\frac{1}{\lVert \mathbf{w} \rVert}$만 남게 됩니다.

결국 최적화해야하는 문제는 $\frac{1}{\lVert \mathbf{w} \rVert}$를 최대화하는 것입니다. Margin을 최대화하기 위해서는 분리 평면과 데이터 점 사이의 거리를 멀게 만들어야 하기 때문입니다. 여기에 조건으로, 분리 평면과 가장 가까운 점에서 $\mathbf{w}$를 $1$로 정규화하는 것을 추가해야 합니다.

그러나 조건에 Minimize가 들어있으면 최적화 문제를 풀기 어렵기 때문에, 문제를 조금 변형시킬 필요가 있습니다. $\lvert \mathbf{w}^{\sf T} \mathbf{x}_n + b\rvert$는 $y_n (\mathbf{w}^{\sf T} \mathbf{x}_n + b)$로 대체할 수 있습니다. 왜냐하면, 이 문제에서는 선형 분리가 가능한 데이터 집합을 가정했기 때문에, 모든 데이터가 올바르게 분류되는 상황만을 따지기 때문입니다. 만약에 데이터가 $+1$로 분류된다면 $y_n = 1, -1$로 분류된다면 $y_n = -1$이 되므로 절대값과 동일한 기능을 가짐을 알 수 있습니다.

또한 목적 함수도 분모에 Euclide Norm이 불편하기 때문에 식을 Maximize로 수정해주고, $\mathbf{w}$에 대한 2차식으로 바꾸어줍니다. (이 부분은 아직 이해가 덜 되어 추후 그 이유를 추가하겠습니다)

최종적으로 바꾼 식을 보시면 조건 부분이 $1$과 같은 것이 아니라 $1$ 이상으로 바뀌었습니다. 만약에 모든 조건식이 $1$보다 크다면, 단순히 $\mathbf{w}$와 $b$를 조절함으로써 제일 $1$에 가까운 식을 $1$로 맞춰줄 수 있기 때문입니다.

The solution

이제 이전 슬라이드에서 유도한 최적화 식을 해결하는 방법을 알아보겠습니다.

최적화 문제에서 많이 사용되는 라그랑주를 사용하고자 합니다. 그런데 조건에 부등식이 들어가 있습니다. 이렇게 조건에 부등식이 들어간 라그랑지안을 KKT (Karush Kuhn Tucker) 라고 합니다. KKT는 대학원 수업에서 다루는 Convex Optimization에 나오는 내용인데, 이 강의에서 구체적으로 KKT를 풀지는 않으니 일단 이런 것이 있다고만 생각하고 넘어가도록 합시다.

이 문제를 쉽게 풀기 위해 이전에 정규화에서 배웠던 방법을 생각해봅시다. 왜냐하면 이 때도 조건에 부등식이 들어간 목적 함수를 최소화하는 문제를 풀었기 때문입니다. 단지 차이는 목적 함수가 $E_{in}$이 $\mathbf{w}^{\sf T} \mathbf{w}$으로 바뀌고, 조건이 $\mathbf{w}^{\sf T} \mathbf{w}$에서 $E_{in}$으로 바뀌었을 뿐입니다. 갑자기 SVM의 조건에 $E_{in}$을 언급하는 이유는, 모든 데이터가 올바르게 분류된다고 가정했기 때문에 $E_{in}$이 0이여만 하기 때문입니다.

라그랑주 승수법(Lagrange Multiplier)에 의해, 조건으로 붙은 $y_n(\mathbf{w}^{\sf T} + b) - 1$은 목적 함수로 들어갑니다. 이 라그랑지안을 $\mathbf{w}$와 $b$에 대해 풀어야 합니다.

그 후 주어진 라그랑지안을 최소화하는 해법을 찾기 위해, $\mathbf{w}$에 대해 기울기(Gradient)가 0이 되는 지점을 구해야 합니다. 다행히도 라그랑지안의 첫번째 항은 $\mathbf{w}$에 대한 2차식, 두번째 항은 $\mathbf{w}$에 대한 1차식이기 때문에 기울기는 간단하게 구할 수 있습니다.

마찬가지로 라그랑지안을 $b$로 편미분을 하게 되면 첫번째 항은 $b$가 포함되지 않았으므로 0, 두번째 항은 $b$에 대한 1차식이므로 역시 간단하게 구할 수 있습니다. 이 편미분 식 역시 0이 되는 지점을 찾아야 합니다.

이전에 구한 식들을 정리해보겠습니다. 정리 자체는 매우 간단합니다. 기존의 라그랑지안 식에서, 이전에 구한 $\mathbf{w}$와 $\sum_{n=1}^{N} \alpha_n y_n$만 대입하면 라그랑지안 식에서 $\mathbf{w}$와 $b$는 모두 사라지게 되고, 라그랑지안 식은 $\alpha$에 관한 식으로 변하게 됩니다.

(추후에 자세한 정리 과정을 여기에 적겠습니다)

결국 최종적으로 풀어야 하는 식은 Quadratic Programming 문제가 됩니다. 여기서 직접 QP 문제를 풀 필요는 없습니다. 왜냐하면 MATLAB, Python 등의 라이브러리에서 QP를 풀어주는 기능이 이미 존재하기 때문입니다. 지금까지 유도한 QP 문제만 넣어주면 알아서 답이 나오기 때문에, 여기에서는 QP 문제 해결 방법은 생략하도록 하겠습니다.

다만 주어진 문제는 Maximize를 해야 하는데, QP 문제는 일반적으로 Minimize를 시키게 되어있습니다. 따라서 식의 부호를 반대로 하고 Maximize를 Minimize하는 문제로 바꾸겠습니다.

그리고 앞의 식에서 $\alpha$와 $\mathbf{x}$, $y$를 구분해주기 위해 식을 변형시켜 $\alpha$를 앞으로 따로 빼고 나머지는 Matrix로 표현했습니다.

식 자체가 매우 복잡해보이지만, 단지 프로그램에 넣기 편하게 만들기 위해 식을 풀어쓴 것입니다. 간단하게는 아래처럼 표현할 수 있습니다.

\[\min \frac{1}{2} \alpha^{\sf T} \mathbf{Q} \alpha - \mathbf{1}^{\sf T} \alpha\] \[\text{subject to }\mathbf{y}^{\sf T} \alpha = 0; \alpha \ge 0\]

QP 문제를 제시하는 것까지는 성공적이었으나, QP 문제를 컴퓨터가 풀어준다고 해도 여전히 문제점이 있습니다. 특히, Quadratic Coefficients로 표현된 Matrix는 $N \times N$ 크기이기 때문에 데이터가 많이 주어질수록 푸는데 시간이 오래 걸린다는 문제가 있습니다. 그렇기에 현재 이런 문제를 쉽게 풀기 위한 경험적인 방법이 연구되고 있습니다.

계산상의 문제는 별개의 문제이기 때문에 여기서는 일단 성공적으로 $\alpha$를 구했다고 가정해봅시다. 그 다음에는 당연히 $\mathbf{w}$를 구해야하는데, 이것은 굉장히 쉽습니다. $\mathbf{x}$와 $y$는 주어진 데이터이기 때문에 당연히 알고있는 것이고, 여기에 방금 구한 $\alpha$만 대입한다면 자연스레 $\mathbf{w}$가 계산되기 때문입니다.

둘째로 볼 것은 KKT 조건에서 Slack이라고 불렸던 식입니다. 이 식이 0이 되므로 $\alpha$ 또는 $(y_n ( \mathbf{w}^{\sf T} \mathbf{x}_n + b) - 1 )$이 0이 되어야 합니다. 이것은 이전에 정규화에서 배웠던 것과 비슷하게 볼 수 있습니다. $\alpha$가 0이라는 것은 라그랑지안이 0이 되었다는 뜻이므로 데이터 점이 아예 Margin 바깥에 있음을 의미합니다. 즉, 이것은 신경을 쓸 필요가 없습니다.

중요한 점은 $(y_n ( \mathbf{w}^{\sf T} \mathbf{x}_n + b) - 1 )$이 0이 되는 지점입니다. 이 말은 데이터 점이 정확하게 Margin의 경계선에 있다는 것을 의미하기 때문입니다. 이 때의 점 $\mathbf{x}_n$은 Margin의 범위를 도와주기 때문에 Support Vector라고 부릅니다.

Support Vector를 직관적으로 이해하려면, 위 슬라이드의 오른쪽 그림을 참고하시면 됩니다. 보라색 선은 데이터 집합을 구분하는 분리 평면이 되고, 노란색 영역은 Margin이 됩니다. 노란색 영역의 경계선을 보시면 경계에 걸쳐있는 점이 표시되어 있는데, 이 점들이 바로 Support Vector입니다. 이전 슬라이드에서 $(y_n ( \mathbf{w}^{\sf T} \mathbf{x}_n + b) - 1 )$이 0이 되는 점이었습니다. 그리고 바로 이전 슬라이드에서 $\alpha$가 0이 되는 점들이 Margin 밖에 있는 데이터입니다.

지금까지 $\alpha$와 $\mathbf{w}$만 구했지, $b$를 아직 구하지 않았습니다. $b$를 구하는 방법도 간단한데, Support Vector가 아닌 데이터에서는 $\alpha$가 0이 되므로 $b$를 구하는데 쓸 수 없습니다. 그렇기에 Support Vector를 먼저 구한 다음, 아무 Support Vector 데이터를 가져오면 $y_n ( \mathbf{w}^{\sf T} \mathbf{x}_n + b) = 1$이란 간단한 식이 나오므로, $\mathbf{w}$만 대입하면 $b$를 구할 수 있습니다.

Nonlinear transforms

지금까지는 선형 분리가 가능한 경우를 가정했지만, 이제 Support Vector를 Nonlinear Transform에 응용해보도록 하겠습니다.

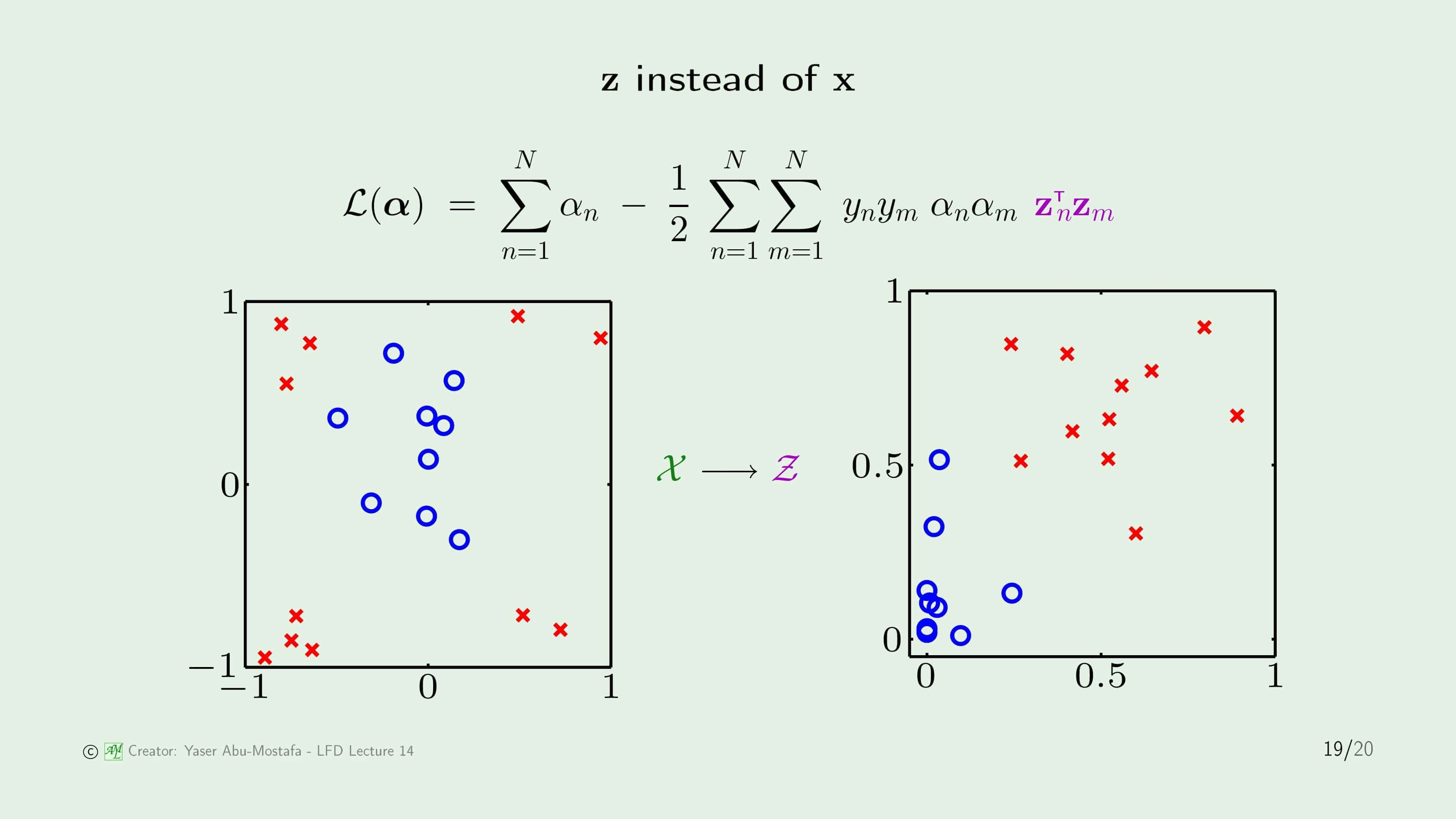
일반적이 Nonlinear Transform은 기존의 데이터 $\mathbf{x}$를 Transform Function을 통해 $\mathbf{z}$으로 바꾸어줬습니다. $\mathbf{x}$는 선형 분리가 불가능한 데이터이지만, Transform을 통해 선형 분리가 가능한 $\mathbf{z}$로 바꾼 것입니다.

데이터를 Transform 해도 라그랑지안은 그렇게 크게 바뀌지 않다는 걸 눈치채셨을 겁니다. $\alpha$를 푸는 QP 문제는 어차피 데이터의 “수”에만 영향을 받기 때문입니다. 즉, 데이터를 Transform 하는 것은 Support Vector를 구하는 것을 어렵게 만들지 않습니다.

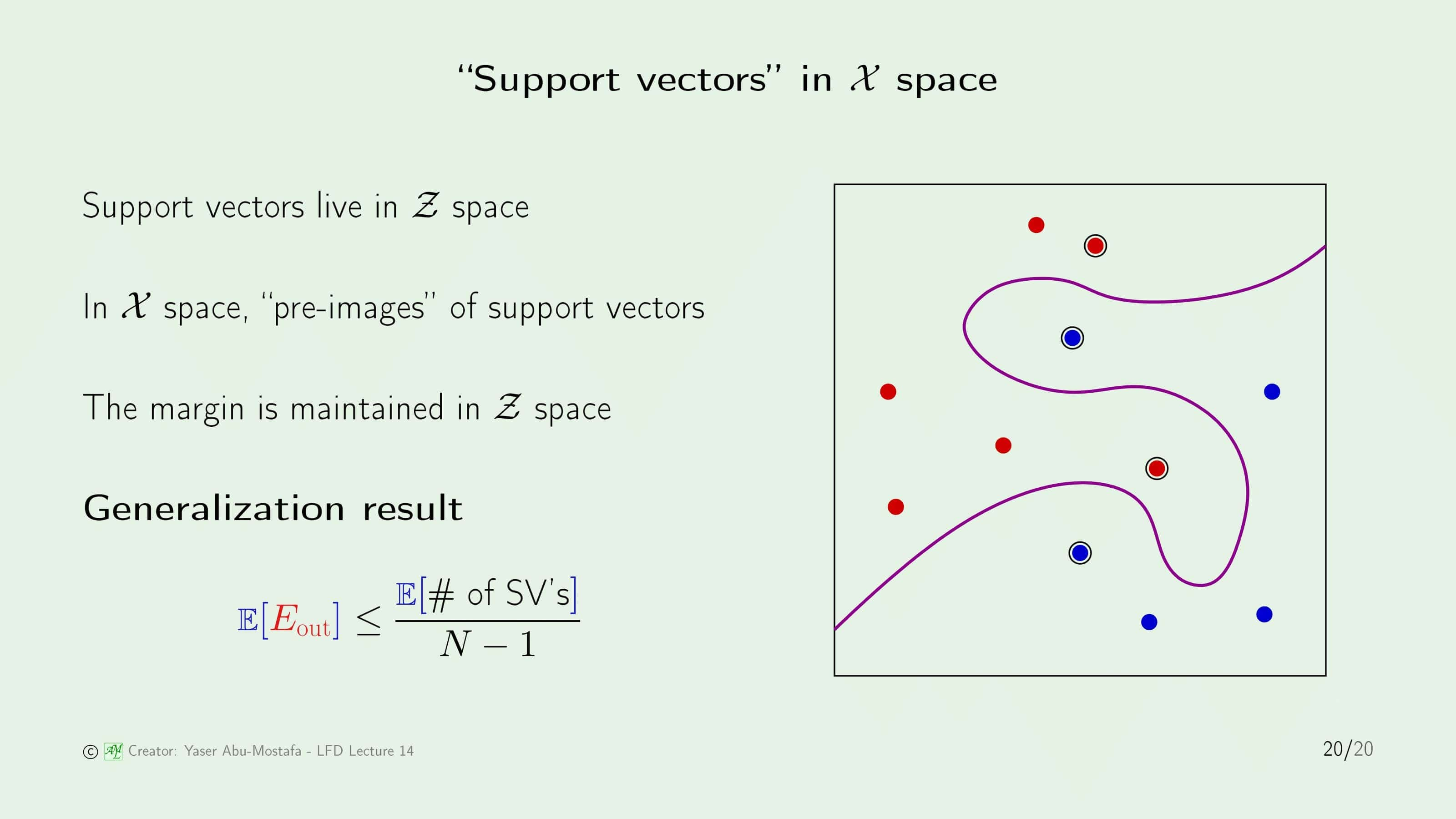
$\mathcal{Z}$ 공간에서 $\alpha$와 Support Vector를 구한 다음 데이터 집합을 다시 $\mathcal{X}$ 공간으로 Transform하게 되면 위 그림과 같은 분리 평면이 나오게 됩니다. $\mathcal{Z}$ 공간에서는 분리 평면이 직선과 같은 형태지만, $\mathcal{X}$ 공간에서는 이렇게 곡선 형태로 나오게 됩니다. Support Vector는 그림상에 특별하게 표시가 되어있습니다.

분리 평면을 언뜻 보면 Overfitting을 일으킬 것처럼 생겼습니다. 하지만 이 문제에서는 Support Vector가 4개로 나오는데, 이 말은 $\mathcal{Z}$ 공간에서 $\mathbf{w}$는 4개의 Parameter만 있다는 뜻입니다. 그렇기에 Support Vector는 일반화에 매우 적합한 특징을 갖고 있다고 볼 수 있습니다.

Support Vector에서의 일반화를 명확하게 정리하면, 평균적인 Out of Sample Error는 Support Vector의 수의 평균을 $N-1$로 나눈 것보다 작습니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.