The Learning Problem

1장은 어떤 것이 Learning Problem인가에 대해 설명하는 강의입니다.

타이틀 슬라이드의 오른쪽 아래를 보시면 무언가 기하학적인 모양이 나와있는 그림이 있는데, 저번 글과 비교해 보시면 교재 표지에 똑같은 그림이 나와있다는 것을 알 수 있습니다. 이 그림은 추후 또 나올 그림이니 기억해 두시길 바랍니다. 나중에 이 그림이 다시 나왔을 때 또 언급하겠습니다.

Outline

이번 장은 총 다섯 부분으로 구성되어 있습니다. 첫째로 기계학습의 예시를 보여주고, 둘째로 기계학습의 구성 요소를 설명합니다. 셋째로 간단한 예시 모델을 설명하며, 넷째로 기계학습의 종류를 설명합니다. 마지막으로 간단한 퍼즐을 통해 이번 장에서 배운 내용을 점검하게 됩니다.

Example of Machine Learning

먼저 간단한 기계 학습의 예시를 들면서 시작하겠습니다.

만약 관객이 영화를 관람한 후, 그 영화에 평점을 몇 점 매길 것인가 예측하는 문제가 있다고 가정해봅시다. 넷플릭스 같이 영화를 판매하는 회사들은 해당 유저가 높은 평점을 매길 영화(즉, 좋아할 만한)를 예측하여 유저에게 추천하는 기능이 있습니다. 당연히 예측의 정확도가 높을 수록 그 회사의 수익이 증가하게 되므로, 이 정확도를 높일 수 있는 방법을 꾸준히 연구하고 있습니다. 강의에서 언급하길, 실제로 넷플릭스의 추천 기능을 10% 향상을 시키는 사람에게 백만달러의 상금을 걸었다고 합니다.

이런 문제를 기계학습으로 해결 할 수 있을까요?

주어진 문제를 기계학습으로 해결하기 위해서는 다음 3가지 조건이 반드시 필요합니다.

1. 패턴이 존재해야 한다.
2. 이를 수학적으로 나타낼 수 없어야 한다. (예를 들면 정확한 함수)
3. 데이터를 가지고 있어야 한다.

1번 조건부터 하나씩 따져봅시다. 만약 데이터에 패턴이 존재하지 않고 결과값이 무작위로 나온다면 해당 문제는 기계학습으로 풀 수 없습니다. 하지만 영화 추천 문제의 경우, 사람마다 선호하는 영화의 스타일이 존재하므로 패턴이 존재한다고 말할 수 있습니다.

2번 조건은 조금 이상하게 느껴질 수도 있습니다. 이 말은 만약 사람을 입력으로 넣고, 그 사람의 취향이 완벽히 반영되어 어떤 영화를 선호하는지 결과값으로 출력할 수 있는 함수를 구할 수 있으면 안된다는 것입니다. 만약 구할 수 있다면, 그것을 그냥 계산하면 되므로 굳이 기계학습을 쓸 필요가 없습니다. 위에서 언급한 넷플릭스의 예시는 영화의 선호도를 완벽하게 나타낼 수 있는 함수를 구할 수 없으므로, 이 조건도 만족한다는 것을 알 수 있습니다.

3번 조건은 너무나 당연한 조건입니다. 예를 들어, 만약 어떤 사람이 태어나서 영화를 한 편도 보지 않았다면 이 사람이 어떤 영화를 좋아하는지 전혀 알 수 없을 것입니다. 이 조건은 셋 중 가장 중요한 조건으로써, 책 제목조차 Learning From Data 로 이 조건을 강조하신 걸 아실 수 있을 것입니다. 영화 추천 대상을 영화를 한번 이상 본 사람들로 한정한다면, 이 조건도 만족하다고 볼 수 있습니다.

따라서, 세 조건을 모두 만족하므로 영화를 추천하는 문제는 기계학습으로 해결할 수 있다고 말할 수 있습니다.

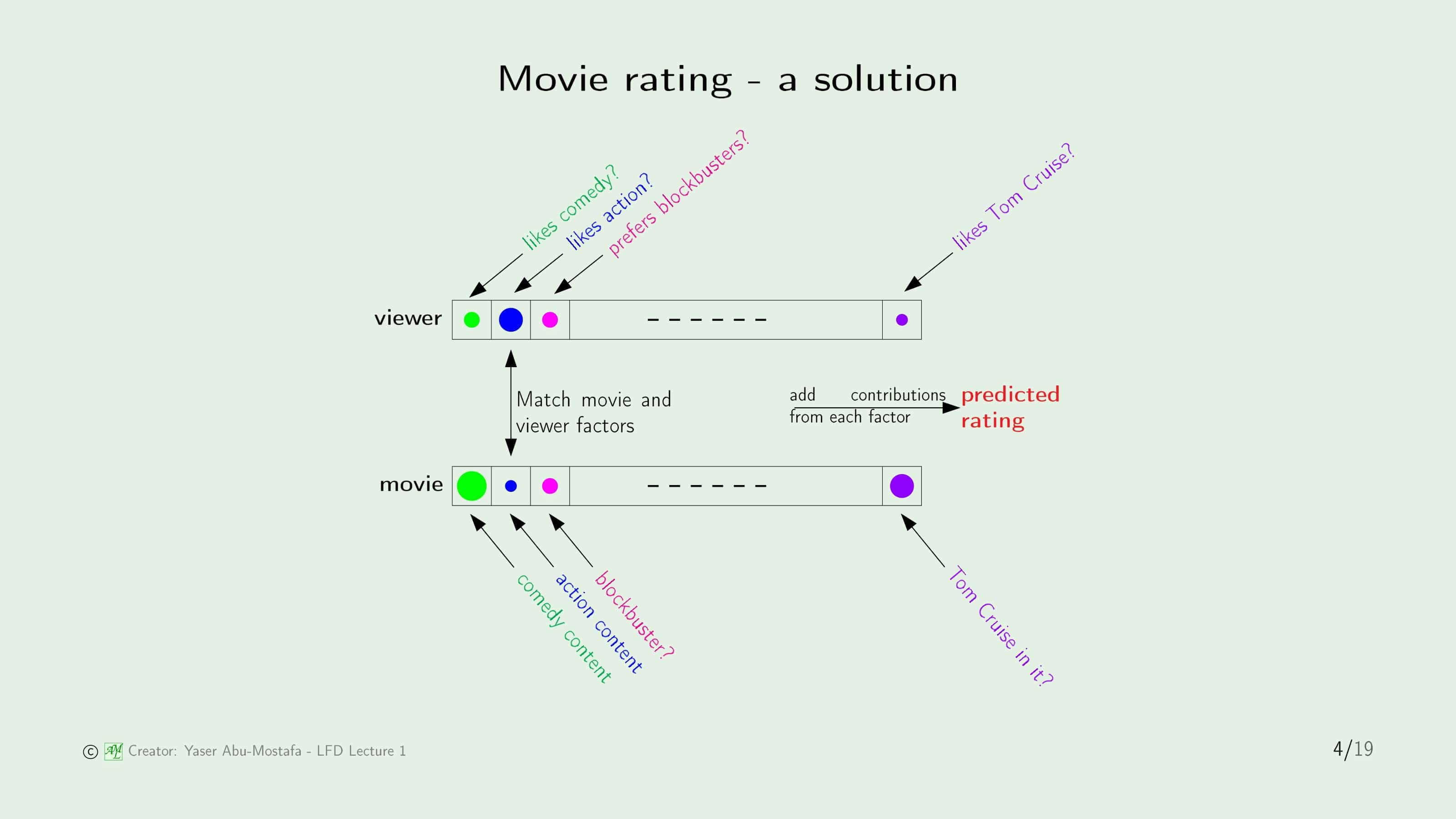
그럼 이 문제를 한번 분석해봅시다.

사람마다 어떤 요소를 선호하는지 위의 그림과 같이 Vector (벡터)로 표현한다고 가정해 보겠습니다. Viewer Vector에서 각 요소의 동그라미 크기는 이 사람이 해당 요소를 얼마나 좋아하는지에 대한 수치입니다. comedy를 나타내는 원의 크기보다 action을 나타내는 원의 크기가 더 크므로, 이 Viewer는 action 영화를 comedy 영화보다 더 좋아한다는 것을 알 수 있습니다. 영화의 종류 외에도, 배우에 대한 선호도도 영화를 평가하는데 중요한 요소일 것입니다. 이 예시에서는 해당 Viewer가 톰 크루즈를 얼마나 좋아하는가를 예시로 들었습니다.

비슷한 방법으로 영화들도 이러한 Vector로 표현할 수 있을 것입니다. 이 영화의 comedy 요소는 어느 정도인가, action 요소는 어느 정도인가, 톰 크루즈가 나오는가 같은 방식으로 말입니다. 이렇게 Viewer와 영화를 각각 벡터로 표현한다면, 이 두 벡터를 비교하여 Viewer가 과연 해당 영화를 좋아할지 아닐지에 대한 평가가 가능합니다. 대표적으로 두 벡터 사이의 Norm (거리)을 계산하는 방법이 있습니다.

그러나, 이 방법은 단순한 해결 방법의 한 종류일 뿐, 기계학습으로 해결했다고 말할 수 없습니다.

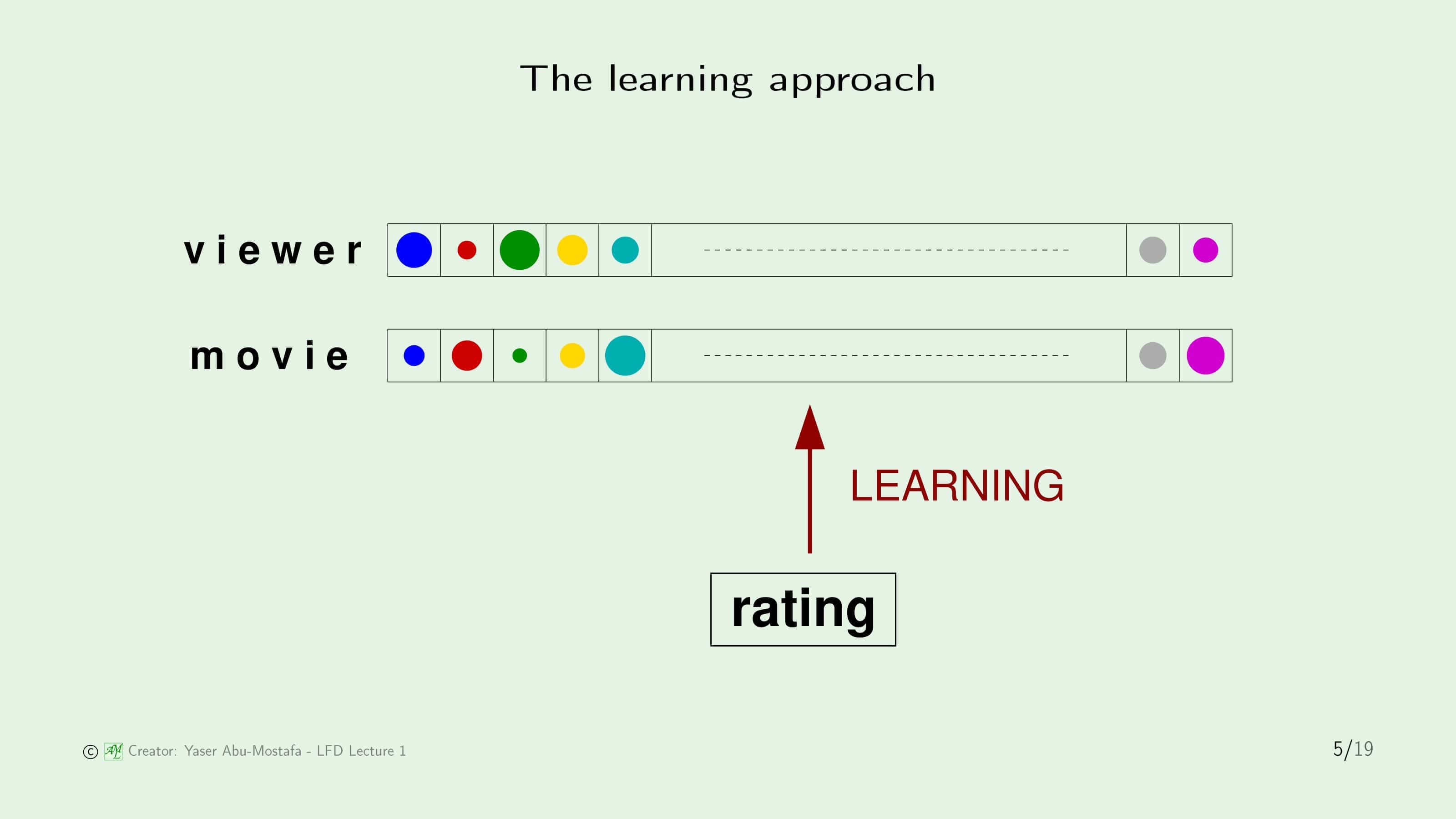
그럼 어떤 방식으로 해결해야 기계학습으로 해결했다고 말할 수 있을까요?

이전 슬라이드에서는 Viewer의 Vector와 영화의 Vector가 얼마나 다른가에 따라 선호도를 파악할 수 있다고 했습니다.

그런데, 과연 이 차이만으로 Viewer가 어떤 영화를 선호할 지 구분할 수 있을까? 라는 의문이 생깁니다.

쉽게 설명하기 위해, 예시를 하나 들어보겠습니다. Viewer A, B 두 사람이 존재한다고 가정해보겠습니다. 그리고 정말 우연히도, 이 두 사람이 둘다 comedy를 싫어하고 톰 크루즈를 좋아한다고 가정해봅시다. 그리고 새로운 영화가 나왔습니다. 이 영화는 톰 크루즈가 나오는 comedy 영화라고 가정해봅시다. 그렇다면 A, B 두 사람이 이 영화에 내리는 판단이 같을까요? 조금만 생각해봐도 당연히 아니라는 것을 알 수 있습니다. 예를 들어, A는 톰 크루즈를 너무 좋아해서 비록 싫어하는 comedy 영화라도 높은 평가를 할 수 있고, B는 comedy가 너무 싫어서 아무리 좋아하는 톰 크루즈가 나왔다고 해도 낮은 평가를 내릴 수 있기 때문입니다.

따라서, 사람들마다 각 요소에 다른 가중치를 갖고 있다는 것을 알 수 있습니다. 어떤 사람은 장르에 더 비중을 둘 수 있고, 어떤 사람은 배우에 더 비중을 둘 수도 있습니다. 이러한 가중치까지 반영하여 각 Viewer가 어떤 영화를 좋아할 지(=높은 평가를 할지) 예측하는 것이 바로 기계학습이라고 할 수 있습니다.

Components of Learning

이제 다른 예시를 하나 더 들어봅시다.

만약 당신이 카드 회사에서 카드를 발급해주는 직원이라고 가정해보겠습니다. 그리고 어떤 사람이 당신에게 카드 발급 신청서를 작성하여 제출했습니다. (그 신청서의 내용은 슬라이드에 나와있는 표와 같다고 생각합시다) 이제 당신은 이 사람에게 카드를 발급해 줄 지, 아니면 거부할지 판단해야 합니다.

이 문제를 구체적으로 모델링을 해봅시다. 이전 슬라이드에 나와있는 표의 요소를 Input $\mathbf{x}$로 설정합니다. 즉, $\mathbf{x} =$ (나이, 성별, 연봉, …) 으로 이루어진 Vector입니다. $y$는 해당 Input $\mathbf{x}$에 대한 Output입니다. 카드를 발급해준다면 $y = +1$, 그렇지 않다면 $y = -1$ 입니다. 그리고 Input $\mathbf{x}$와 결과 $y$를 완벽하게 매칭한 함수 $f$가 있다고 가정해봅시다. 3번 슬라이드에서도 언급했듯이, 이 함수는 당연히 구할 수 없습니다. 하지만 이 함수를 구하는 것이 궁극적인 목적이므로, 이 함수의 이름을 Target Function이라 부릅니다.

Data는 지금까지 카드를 발급하거나 거부했던 지원자들의 목록입니다. 이를 기반으로 새로운 지원자의 카드 발급 여부를 결정할 것입니다. 이를 통하여 우리의 목적은 ($f$라고 예상되는) Hypothesis function $g$를 도출하는 것입니다.

이전 슬라이드의 요소들을 도식화하면 위와 같습니다.

먼저, Target function $f$가 존재하지만(당신의 개인적인 카드 발급 기준) 그걸 구할 수는 없습니다. 하지만 지금까지 카드를 발급해주거나 거부했던 기록들은 모두 이 함수 $f$로부터 도출된 데이터라고 볼 수 있습니다.

이 기록들을 Training Examples, Training Set, 또는 간단하게 Sample 로 부릅니다.

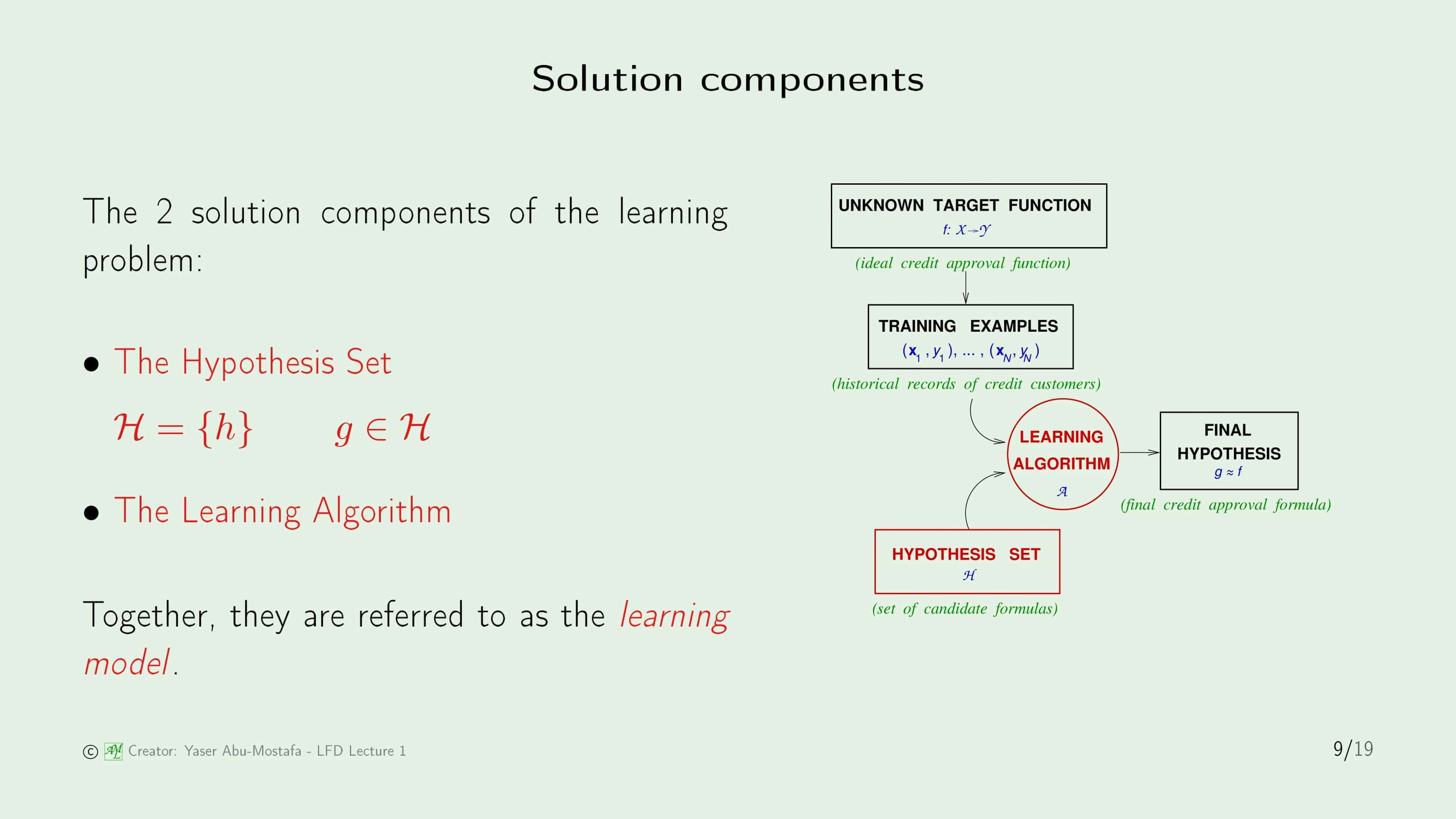
Hypothesis Set은 이 데이터를 통해 함수 $g$를 구할 수 있는 후보입니다. 가령 모든 지원자들의 카드 발급을 거부한다는 것도 하나의 Hypothesis라고 볼 수 있습니다. 이런 것들을 포함해 모든 Hypothesis들의 집합이 바로 Hypothesis Set입니다. 쉽게 얘기하자면, 정답 후보들의 집합이라고 이해하시면 됩니다. 그렇다면 이제 정답(이라고 생각되는 것)을 구하기 위해 여러분이 갖고있는 데이터와 이런 가설을 묶어 Learning Algorithm을 사용해 Final Hypothesis를 결과물로 도출합니다. Learning Algorithm이라는 것은 앞으로 배울 Perceptron Learning Algorithm이라던가, Neural Network라던가, Support Vector Machine 등을 일컫는 말입니다. 이 두 가지를 합쳐 Learning Model 이라 부릅니다.

당연히 Final Hypothesis는 이들 중에 가장 정확도가 높은(갖고있는 데이터에 가장 잘 들어맞는) 것을 고르는 것이 됩니다.

A Simple Model

이해를 돕기 위해 구체적인 하나의 Model로 예시로 들어보겠습니다. 이 방법은 Perceptron이라고 합니다.

Input $\mathbf{x}$는 앞에서 언급한 바와 같이 고객의 정보를 Vector로 나타낸 것입니다. 이 Vector에는 총 $d$ 종류의 값이 저장되어 있습니다.

영화 예제에서와 같이, 고객의 정보에서 특히 중요한 요소도 있고, 그렇지 않은 요소도 있을 것입니다. 이렇게 중요도를 표현한 값을 Weight (가중치)라 하고, 이들을 모은 것을 Weight Vector $\mathbf{w}$ 라고 정의하겠습니다. 당연히 모든 고객의 정보에 대한 Weight를 곱해줘야하니, $\mathbf{w}$는 $d$차원의 Vector임을 알 수 있습니다. 즉, $\mathbf{w} = (w_1, w_2, …, w_d)$ 라 쓸 수 있습니다. 고객의 정보에서 이 Weight들을 곱해 하나의 Scalar로 표현해봅시다. 그럼 아래와 같이 정리할 수 있습니다.

\[w_1 x_1 + w_2 x_2 + ... + w_d x_d = \sum_{i=1}^d w_i x_i\]

이제 이 계산된 Scalar을 기준으로 카드를 발급할 지, 거부할 지 결정해야 합니다. 당신이 생각한 기준치를 Threshold라고 합시다. 위의 가중치가 반영된 고객 정보의 총 합이 Threshold보다 크다면 당신은 카드를 발급해줄 것이고, 아니라면 거부할 것입니다. 이를 하나의 Hypothesis $h$ 라 한다면, 위 슬라이드의 마지막 식처럼 표현할 수 있습니다.

$\text{sign}$의 의미는 괄호 안의 값이 양수이면 $+1$이고 음수이면 $-1$의 값으로 정한다는 뜻입니다. 예를 들어 $\text{sign}(-0.2) = -1$, $\text{sign}(3.4) = +1$ 입니다. 식에서 빨간색으로 표현된 값들이 구해야 할 값들입니다. ($x_i$는 고객의 데이터로 처음부터 주어진 값이기 때문에 구할 필요가 없습니다)

표현을 조금 간단하게 하기 위해, 식을 수정해보겠습니다.

Threshold를 $w_0$으로 표현하겠습니다. 눈썰미가 좋으신 분들은 이전 슬라이드와 비교해보시고 왜 Threshold를 빼는 식이 갑자기 덧셈으로 바뀌냐? 라고 생각하실겁니다. 하지만 덧셈으로 하든 뻴셈으로 하든 큰 차이는 없습니다. $w_0$를 음수로 설정한다면 어차피 똑같은 식이 되니까요. 굳이 음수로 설정하면서까지 덧셈으로 바꾼 이유는 앞의 Sigma 연산과 합치기 위해서입니다.

하지만 Weight Vector $\mathbf{w}$와 Input Vector $\mathbf{x}$는 모두 $d$차원 Vector였기 때문에, Sigma 연산과 하나로 합치기 위해서는 $x_0$이 필요합니다. $w_0$은 어차피 Threshold 값이라 $x_0$가 의미 없으므로, 편의상 $x_0 = 1$로 설정합니다. 그렇게 되면 결국 괄호 안의 Sigma 연산은 $w_0 x_0 + w_1 x_1 + … + w_d x_d$가 되므로 두 Vector $\mathbf{w}$와 $\mathbf{x}$의 Inner Product (내적)라 할 수 있을 것입니다.

이를 Matrix (행렬)로 표현한다면, 위 식의 마지막 식 처럼 $\mathbf{w}$의 Transpose Matrix (전치행렬)과 $\mathbf{x}$의 곱으로 표현할 수 있습니다.

방금까지 유도해낸 Hypothesis $h$ (Perceptron)는 결국 두 Vector(또는 Matrix)의 곱으로 이루어진 Linear (선형)식이기 때문에 이 방법으로 데이터를 완벽하게 구분하려면(카드를 발급해줄 사람과 거부해줄 사람을 구분하려면) 반드시 데이터를 직선 하나로 나눌 수 있어야 합니다. 이것을 Linearly Separable 데이터라고 합니다.

그럼 이 Perceptron에서 Weight Vector $\mathbf{w}$를 구하는 것이 목적이 되었습니다. 여기서는 간단한 알고리즘인 Perceptron Learning Algorithm (PLA)을 소개합니다.

알고리즘을 시작하기 전에, Weight Vector $\mathbf{w}$는 임의의 값으로 초기화합니다. (Zero Vector로 초기화하는 것이 가장 무난합니다)

방금까지 정한 Perceptron Hypothesis $h$ 에 기존에 갖고있던 Training Set을 하나씩 대입합니다. (이 Training Set은 과거에 당신이 카드를 발급해주거나 거부했던 데이터이기 때문에 올바른 $y$ 값이 존재합니다) 대입을 했을 때 올바른 결과가 나오는 경우 (즉, $sign(\mathbf{w}^T \mathbf{x}_n) = y_n$인 경우)에는 그냥 넘어갑니다. 하지만 만약 Training Data를 넣었을 때 다른 경우가 나온다면 (즉, $sign(\mathbf{w}^T \mathbf{x}_n) \neq y_n$인 경우) 아래와 같이 Weight Vector $\mathbf{w}$를 업데이트 합니다.

\[\mathbf{w} = \mathbf{w} + y_n \mathbf{x}_n\]

그렇게 하면 위 슬라이드의 오른쪽 그림과 같이 Weight Vector $\mathbf{w}$의 방향이 수정됩니다.

이것을 11번 슬라이드에서 보았던 그림처럼 표현한다면 13번 슬라이드의 오른쪽 그림과 같습니다. 분홍색 선이 현재의 Weight Vector $\mathbf{w}$의 위치입니다. (13번 슬라이드 식의 빨간색 $\mathbf{w}$를 의미합니다) 동그라미 친 파란색 (+) 데이터가 Perceptron 식에 대입이 되었다고 가정해봅시다. 그렇다면 이 (+) 데이터는 Misclassified (잘못 분류된) 데이터이기 때문에 (양의 값을 가지는 Output인데 음의 값을 가지는 Output들과 같이 분류되어 있으므로) Weight Vector $\mathbf{w}$의 업데이트가 필요합니다. 따라서 현재의 분홍색 선이 왼쪽방향으로 살짝 휘게 되어 새로운 Weight Vector $\mathbf{w}$가 나오게 됩니다. (13번 슬라이드 식의 파란색 $\mathbf{w}$를 의미합니다)

이 과정이 반복해서 $N$개의 모든 데이터가 올바르게 분류된다면, 이 알고리즘이 끝나게 되고 주어진 데이터를 분류할 수 있는 Weight Vector $\mathbf{w}$가 Output으로 나오게 됩니다.

이 알고리즘이 왜 Linearly Separable 데이터를 정확하게 분류할 수 있는지 의문을 가지시는 분도 계실 것입니다. 당연한 의문입니다. 직관적으로는 왜 이 방법이 분류가 되는지 이해하기 어려워 증명이 필요하기 때문입니다. 다만 여기에 이 증명까지 싣게 되면 분량이 너무 늘어나기 때문에, 대표적인 2개의 증명이 나와있는 링크만 남기겠습니다.

• Haim Sompolinsky 교수님의 증명 [pdf]
• Michael Collins 교수님의 증명 [pdf]

이 외에도 구글에 검색해보시면 여러 증명 방법들이 있습니다.

Types of Learning

이제 기계학습에 어떤 종류가 존재하는지 하나씩 살펴보겠습니다.

기본적으로 학습의 전제는 A Set of Observations (관찰된 결과의 집합)을 사용하여 Underlying Process (근본적인 과정)를 밝혀낸다 입니다. 여기서 Underlying Process가 의미하는 것은 어떤 데이터를 출력하는지에 대한 Probability Distribution (확률 분포)이고, A Set of Observations이란 그 Probability Distribution으로부터 생성된 Data(=Sample)라는 뜻입니다. 이 전제가 굉장히 방대하기 때문에, 이 전제를 만족하는 방법은 수많은 종류가 있습니다.

여기서는 크게 3가지로 나누어 Supervised Learning, Unsupervised Learning, 그리고 Reinforcement Learning이 소개되어 있습니다.

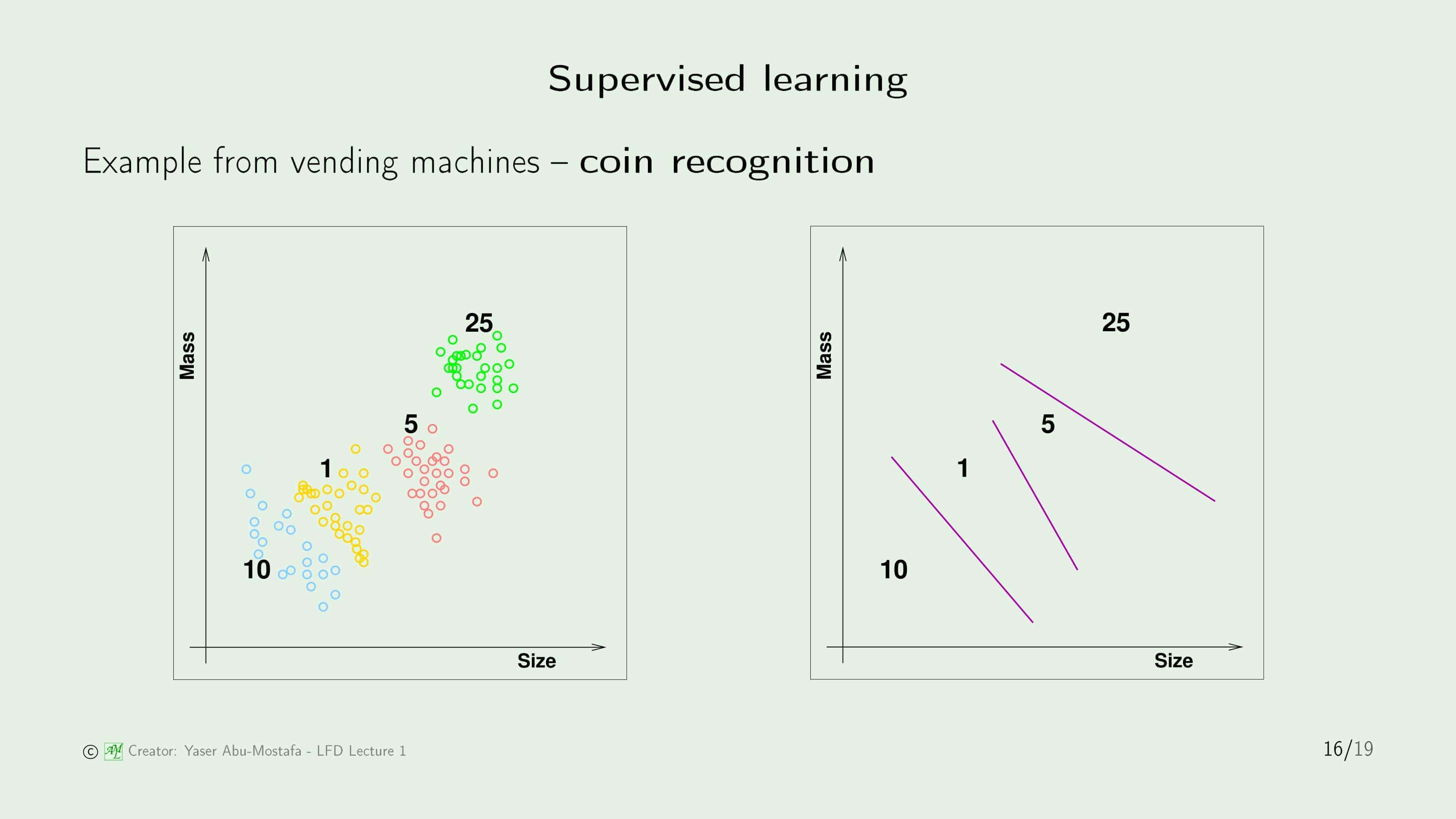
Supervised Learning (지도학습)이란 사람이 데이터를 학습시킬 때 Input $\mathbf{x}$와 정답 Label $y$를 주고 학습시키는 방법입니다.

슬라이드의 예제에서는 자판기에서 사용되는 동전 분류 방법을 제시하고 있습니다. 동전은 종류에 따라(각인되어있는 액수에 따라) 각각 크기와 질량이 다릅니다. 다만 같은 액수의 동전이라고 해도 이것들이 완벽하게 같지는 않습니다. 왜냐하면 동전은 사용되면서 이물질이 묻을 수도 있고, 닳을 수도 있기 때문입니다. 이 예제에서 Supervised Learning을 사용한다면 자판기에 동전을 넣어주면서 이것이 10센트 동전이다, 이것이 25센트 동전이다라고 정답을 입력해주는 것입니다. 이렇게 되면 위 슬라이드의 왼쪽 그림과 같이 각 동전의 크기와 질량 분포를 알 수 있고, 이를 사용하여 오른쪽 그림과 같이 동전을 분류할 수 있는 것입니다.

다음으로 Unsupervised Learning (비지도학습)은 Supervised Learning과는 다르게 Input $\mathbf{x}$만 주고 정답 $y$를 제공하지 않는 방법입니다. 자판기 예제로 돌아가보면, 동전의 크기와 질량을 기준으로 위의 그래프와 같이 명확하게 구분할 수는 있지만, 어느 분포가 어느 액수의 동전인지를 구분할 수 없습니다. 언뜻 보면 왜 쉬운 Supervised Learning을 놔두고 Unsupervised Learning을 사용하는지 의문이 들 수도 있습니다만, 일반적으로 정답이 주어져 있는 데이터보다 주어져 있지 않은 데이터가 훨씬 많으므로 이 방법을 연구하는 것도 상당히 중요합니다. Unsupervised Learning은 주로 Clustering (군집화)을 통해 구현합니다.

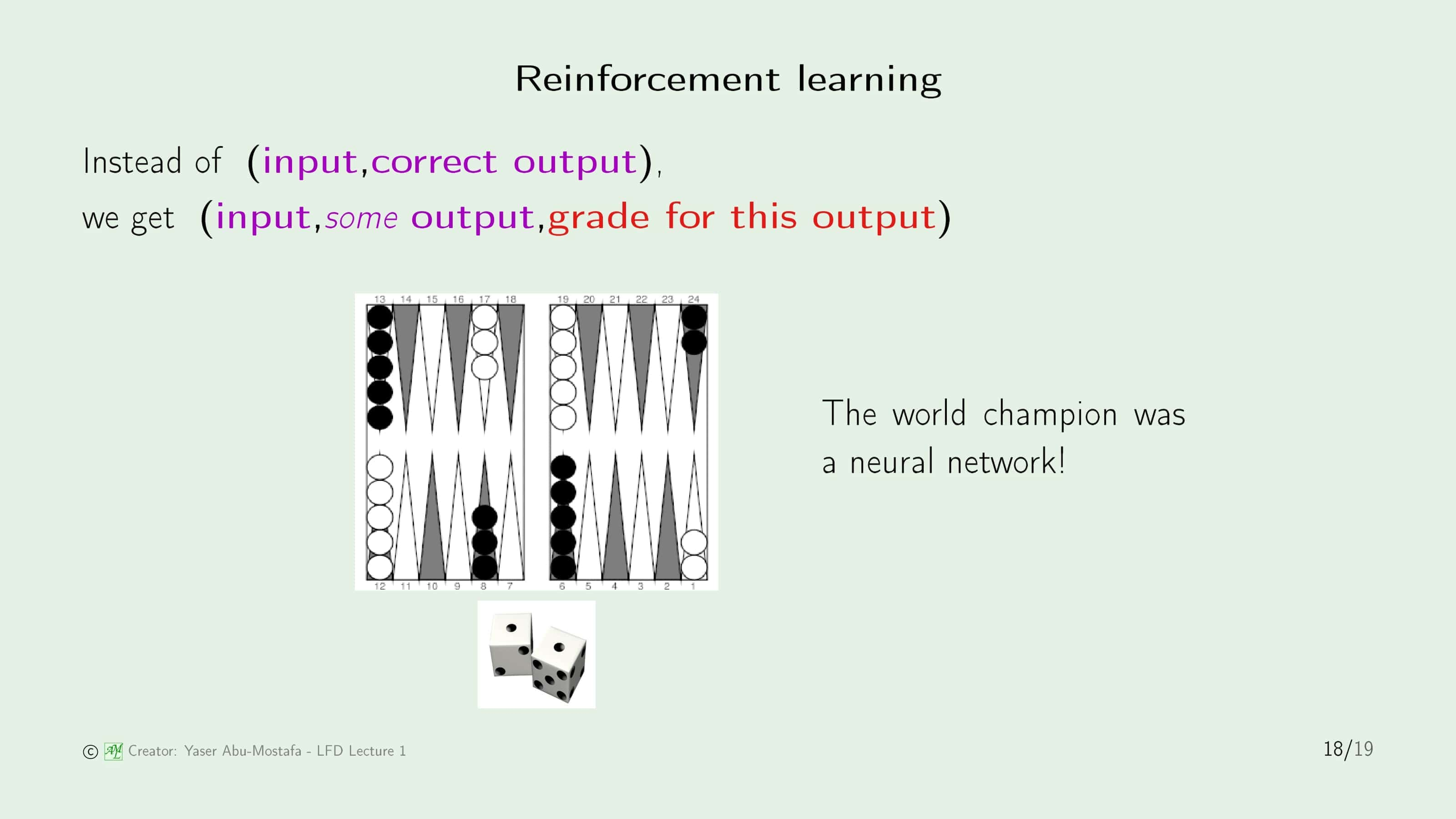
마지막으로 Reinforcement Learning (강화학습)은 Supervised Learning이나 Unsupervised Learning과는 전혀 다른 구조를 갖고 있습니다. Reinforcement Learning도 앞의 두 방법과 마찬가지로 Input $\mathbf{x}$가 주어집니다. 그러나 이 Input에 대해 정답이 주어지는 것이 아니라 이것이 얼마나 괜찮은지에 대한 평가를 하게 됩니다.

이해를 돕기 위해 재밌는 예시를 하나 들겠습니다. 아기들은 손에 잡히는건 뭐든지 입에 넣으려고 합니다. 젖병도 입에 넣고, 사탕도 입에 넣고, … 심지어 신발까지 입에 넣습니다. 이렇게 하나하나 입에 넣어보다가 먹을 수 있는 것들(젖병, 사탕 등)은 긍정적인 평가를 내립니다. 따라서 학습을 한 후 동일한 물건을 발견했을 때엔 역시 입에 넣게 됩니다. 하지만 신발을 입에 넣고 나서는 이게 먹을 수 없는 것이란걸 깨닫습니다. 이런 경우 아기 스스로 신발에 대한 부정적인 평가를 내리고, 다음에 또 다시 신발이 손에 잡힌다면 그 때는 입에 넣지 않는 판단을 하게 됩니다.

이러한 원리 때문에 Reinforcement Learning의 경우 게임과 같은 문제를 해결하는데 가장 널리 이용되고 있습니다. 대표적으로 한창 화제가 되었던 AlphaGo도 Reinforcement Learning을 이용하여 구현한 프로그램입니다. (물론 Reinforcement Learning ‘만’ 사용한 것은 아닙니다)

현재 가장 Hot한 방법으로써 많은 논문에서 언급되고 있습니다. 다만, 본 교재에서는 전반적인 기계학습에 대한 내용만 다루고 있어 이후로는 본 교재나 강의에서 Reinforcement Learning에 대한 언급은 없습니다. 제 연구분야 중 하나가 Reinforcement Learning이기 때문에, 추후 Reinforcement Learning 만을 따로 정리하여 별도로 게시하도록 하겠습니다.

A Learning Puzzle

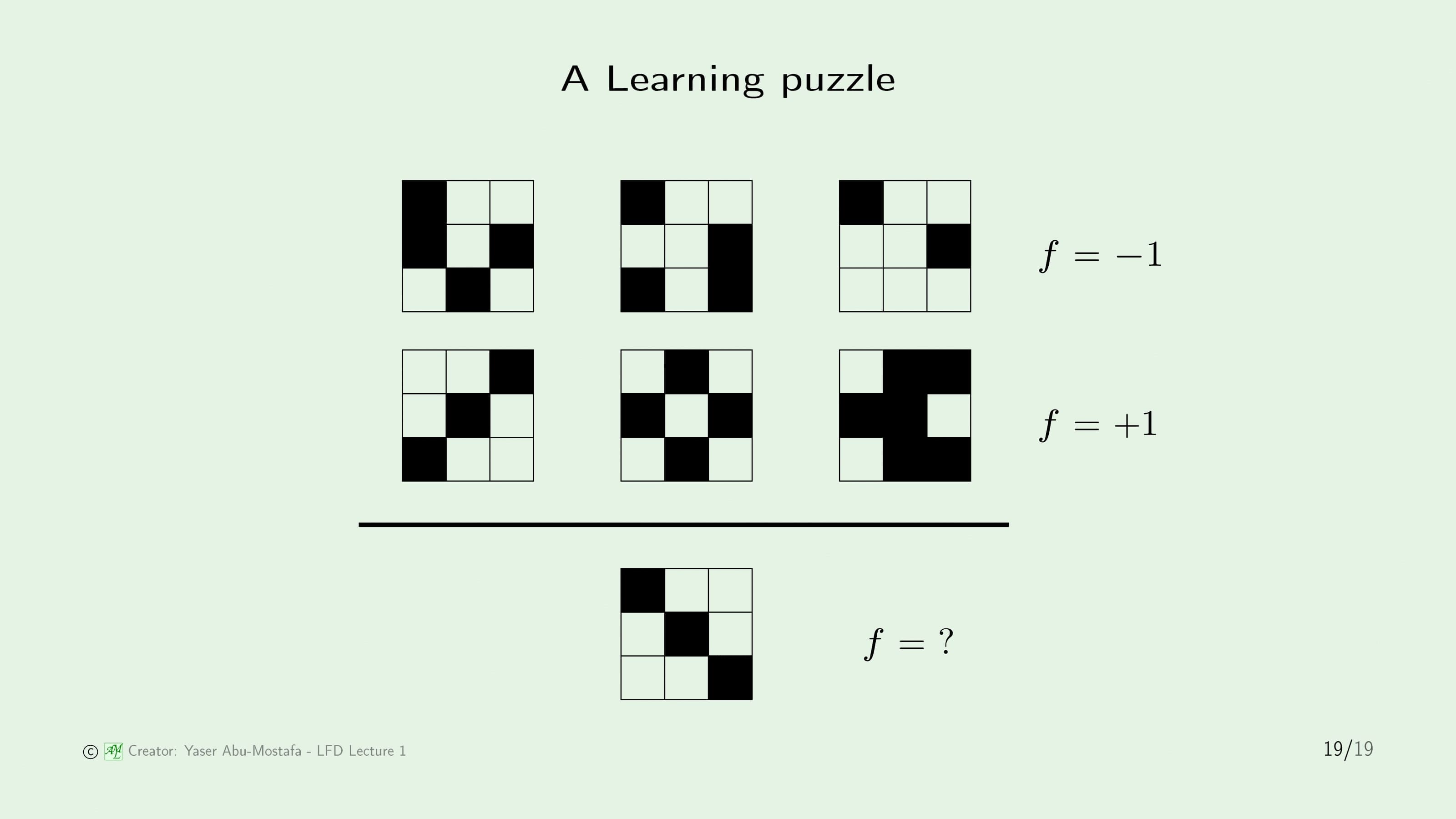
지금까지 배운 내용을 토대로 간단한 퍼즐 문제를 풀어보도록 하겠습니다.

위 3개의 Data는 -1로 분류되었고, 아래 3개의 Data는 +1로 분류되어 있습니다.

그럼 맨 아래의 퍼즐은 무엇으로 분류할 수 있을까요?

정답은 “이 데이터만으로는 +1인지 -1인지 확실하게 결정할 수 없다” 입니다. 앞부분에서 언급했다시피 Target function $f$는 아무도 모르는 것이기 때문입니다. 주어진 데이터만으로 아래의 퍼즐을 분류하기에는 -1로 분류할 수 있는 근거도 있고, +1로 분류할 수 있는 근거도 있습니다. 만약 첫번째 칸이 색칠되어 있는게 -1로 분류하는 기준이다 라고 하면 문제의 퍼즐은 -1로 분류될 것이고, 또는 대칭되어 있는 퍼즐이 +1이다 라고 하면 문제의 퍼즐은 +1로 분류할 수 있기 때문입니다.

그렇다면 데이터를 가지고 학습을 하는건 불가능한 것이 아닌가 하는 의문이 생기게 됩니다. 그 답은 다음 장에 이어서 설명하도록 하겠습니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.