Dynamic Programming

Dynamic Programming은 Markov Decision Process (MDP)와 같이 완벽한 Environment Model이 주어졌을 때 Optimal Policy을 계산할 수 있는 알고리즘입니다. Dynamic Programming은 학부 알고리즘 수업에서도 다루는 중요한 알고리즘이지만, 완벽한 Model이 주어져야 한다는 가정과 막대한 계산 비용으로 인해 강화학습에 직접적으로 적용하기는 힘든 단점이 있습니다. 다만 Dynamic Programming으로 강화학습 문제를 해결하는 과정은 다른 강화학습 해결 방법을 이해하는데 큰 도움이 되기 때문에 반드시 짚고 넘어가야 합니다.

Dynamic Programming을 시작하기 전에, 일단 주어진 Environment가 Finite MDP라고 가정합시다. 지난 장에서 배운 것처럼 Finite MDP는 State, Action, Reward이 유한하고 모든 State $s$와 Action $a$에 대해 Transition Probability $p ( s’, r \mid s, a )$가 제공된 Environment를 말합니다.

강화학습 문제를 Dynamic Programming으로 해결하는 핵심 아이디어는 지난 장에서 배운 Value Function를 계산하여 좋은 Policy을 찾는 것입니다. 즉, Bellman Optimality Equation을 만족하는 최적의 Value Function $v_{*}$ 또는 $q_{*}$를 Dynamic Programming을 사용해 계산하는 것을 보여드리겠습니다.

Policy Evaluation (Prediction)

먼저 임의의 Policy $\pi$에 대해, State-Value Function $v_{\pi}$를 계산하는 방법을 생각해봅시다. Dynamic Programming에서는 이것을 Policy Evaluation이라고 합니다. 또 다른 말로는 Prediction Problem라고도 합니다. 지난 장에서 State-Value Function는 다음과 같이 전개했었습니다.

\[\begin{align} v_{\pi} & \doteq \mathbb{E}_{\pi} \left[ G_t \mid S_t = s \right] \\ \\ &= \mathbb{E}_{\pi} \left[ R_{t+1} + \gamma G_{t+1} \mid S_t = s \right] \tag{from (3.9)} \\ \\ &= \mathbb{E}_{\pi} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) \mid S_t = s \right] \tag{4.3} \\ \\ &= \sum_a \pi (a \mid s) \sum_{s', r} p (s', r \mid s, a) \left[ r + \gamma v_{\pi} (s') \right] \tag{4.4} \end{align}\]

식 (4.4)에서 $\pi (a \mid s)$는 Policy $\pi$에 따라 State $s$에서 Action $a$를 선택할 확률입니다. 기대값 $\mathbb{E}$에서 $\pi$를 붙이는 이유는 Policy $\pi$를 따르기 때문입니다. 만약 $\gamma < 1$이거나 끝이 보장된다면 $v_{\pi}$ 또한 Policy $\pi$에 대해 유일하게 존재한다는 것이 보장됩니다.

Environment를 완벽하게 알 수 있다면 식 (4.4)는 $v_{\pi}$에 대한 연립 일차방정식으로 해결할 수 있습니다. 여기서는 $v_{\pi}$에 대한 근사값을 반복적으로 계산합니다. 초기 근사값 $v_0$를 임의로 정의한 후, 다음과 같이 Bellman Equation의 업데이트 규칙을 사용하여 정확한 $v_{\pi}$에 수렴하게 만들 수 있습니다.

\[\begin{align} v_{k+1} (s) & \doteq \mathbb{E}_{\pi} \left[ R_{t+1} + \gamma v_k (S_{t+1}) | S_t = s \right] \\ \\ &= \sum_a \pi (a | s) \sum_{s', r} p (s', r | s, a) \left[ r + \gamma v_k (s') \right] \tag{4.5} \end{align}\]

Sequence $\{ v_k \}$는 $k \to \infty$일 때 $v_{\pi}$에 수렴합니다. 식 (4.5)와 같은 방법을 Iterative Policy Evaluation이라고 합니다. 구체적인 Iterative Policy Evaluation의 알고리즘은 아래의 Pseudocode를 읽어주시기 바랍니다. 유의하실 점으로 실제 Iterative Policy Evaluation 알고리즘은 이론과 달리 무한히 반복하지 않습니다. 대신 $v_{k+1} (s) - v_{k} (s)$가 임의의 작은 실수 $\theta > 0$보다 작으면 끝나게 됩니다.

Policy Improvement

4.1절에서 Policy에 대한 Value Function을 계산했던 이유는 더 나은 Policy를 찾기 위함입니다. 임의의 Deterministic Policy $\pi$에 대해 Value Function $v_{\pi}$를 구했다면, 이제는 Policy를 변경할 것인지를 고민해봐야합니다. 간단하게 기존 Policy에 대한 Value를 평가했었기 때문에, Policy를 변경했을 때 Value가 높아지는지 그렇지 않은지를 확인해보면 됩니다. 현재 State $s$에서 Action을 $a$로 변경했을 때 Value는 다음과 같습니다.

\[\begin{align} q_{\pi} (s, a) & \doteq \mathbb{E} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s, A_t = a \right] \\ \\ &= \sum_{s', r} p( s', r | s, a) \left[ r + \gamma v_{\pi} (s^{\prime}) \right] \tag{4.6} \end{align}\]

식 (4.6)에서의 핵심은 이것이 과연 $v_{\pi} (s)$ 보다 큰가입니다. 만약 식 (4.6)이 더 크다면 State $s$에 도달할 때마다 Action $a$를 선택하면 기존 Policy보다 더 낫기 때문입니다. 결론부터 말씀드리면 이것은 Policy Improvement Theorem라는 특별한 상황을 만족시킬 경우 참이 됩니다. Policy Improvement Theorem란 모든 State $s \in \mathcal{S}$에 대해, 서로 다른 Deterministic Policy $\pi$와 $\pi^{\prime}$가 주어졌을 때

\[q_{\pi} (s, \pi^{\prime}(s)) \ge v_{\pi}(s) \tag{4.7}\]

를 만족한다면 Policy $\pi^{\prime}$는 Policy $\pi$보다 좋거나 같다는 정리입니다. 즉, 다음과 같이 모든 State $s \in \mathcal{S}$에 대해 기대 Reward가 좋거나 같아야 합니다.

\[v_{\pi^{\prime}}(s) \ge v_{\pi}(s) \tag{4.8}\]

만약 식 (4.7)에서 $\ge$가 아니라 $\gt$를 만족한다면, 식 (4.8) 또한 $\gt$를 만족합니다.

Policy Improvement Theorem는 두 Policy $\pi$와 $\pi^{\prime}$에서 State $s$를 제외한 상황에서 동일한 경우에도 적용됩니다. 식 (4.7)은 양쪽 항이 같을 경우에도 만족하기 때문입니다. 따라서 정확히 하나의 State $s$에서만 $q_{\pi} (s, a) > v_{\pi}(s)$를 만족한다고 해도, Policy $\pi^{\prime}$가 Policy $\pi$보다 낫다고 말할 수 있습니다.

Policy Improvement Theorem는 다음과 같이 전개함으로써 증명할 수 있습니다.

Proof of Policy Improvement Theorem)

\[\begin{align} v_{\pi} (s) & \le q_{\pi} (s, \pi '(s)) \\ \\ &= \mathbb{E} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s, A_t = \pi '(s) \right] \tag{by (4.6)} \\ \\ &= \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s \right] \\ \\ &\le \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma q_{\pi} (S_{t+1}, \pi ' (S_{t+1})) | S_t = s \right] \tag{by (4.7)} \\ \\ &= \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma \mathbb{E} \left[ R_{t+2} + \gamma v_{\pi} (S_{t+2}) | S_{t+1}, A_{t+1} = \pi ' (S_{t+1}) \right] | S_t = s \right] \\ \\ &= \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma R_{t+2} + \gamma^2 v_{\pi} (S_{t+2}) | S_t = s \right] \\ \\ &\le \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 v_{\pi}(S_{t+3}) | S_t = s \right] \\ &\qquad \qquad \qquad \qquad \qquad \vdots \\ & \le \mathbb{E}_{\pi '} \left[ R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \cdots | S_t = s \right] \\ \\ &= v_{\pi '} (s) \end{align}\]

□

이렇게 Policy와 Value Function이 주어지면 특정한 단일 State에서 Policy를 변경했을 때 그 Value를 쉽게 평가할 수 있는 방법을 알게 되었습니다. 이 개념을 확장하여 각각의 State에서 $q_{\pi}(s, a)$에 따라 가장 좋은 Action을 선택하는 Greedy한 Policy를 $\pi^{\prime}$이라고 했을 때, 새로운 Greedy Policy $\pi^{\prime}$는 다음과 같이 정의할 수 있습니다.

\[\begin{align} \pi ' (s) & \doteq \underset{a}{\operatorname{argmax}} q_{\pi} (s, a) \\ \\ &= \underset{a}{\operatorname{argmax}} \mathbb{E} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s, A_t = a \right] \tag{4.9} \\ \\ &= \underset{a}{\operatorname{argmax}} \sum_{s', r} p (s', r | s, a) \left[ r + \gamma v_{\pi} (s') \right] \end{align}\]

이러한 Greedy Policy는 $v_{\pi}$에 따라 단기적으로 가장 좋은 Action을 선택하는 방식으로 Policy Improvement Theorem (4.7)의 조건을 만족합니다. 이렇게 기존 Policy의 Value Function을 사용하여 기존 Policy를 개선하는 새로운 Policy를 만드는 과정을 Policy Improvement라고 합니다.

만약 새로운 Greedy Policy $\pi^{\prime}$이 이전 Policy인 $\pi$만큼 좋지만, 더 좋지는 않다고 가정하면, 식 (4.9)로부터 $v_{\pi} = v_{\pi^{\prime}}$ 이고 모든 State $s \in \mathcal{S}$에 대해 다음과 같이 표현할 수 있습니다.

\[\begin{align} v_{\pi '}(s) &= \max_a \mathbb{E} \left[ R_{t+1} + \gamma v_{\pi '} (S_{t+1}) | S_t = s, A_t = a \right] \\ \\ &= \max_a \sum_{s', r} p(s', r | s, a) \left[ r + \gamma v_{\pi'} (s') \right] \end{align}\]

위 식은 Bellman Optimality Theorem과 동일하므로 $v_{\pi’}$는 $v_{*}$와 동일함을 알 수 있습니다. 즉, Policy $v_{\pi}$와 $v_{\pi’}$는 모두 Optimal Policy입니다. 따라서 Policy Improvement은 원래 Policy가 Optimal인 경우를 제외하고는 반드시 더 나은 Policy를 제공해야 합니다.

지금까지는 모두 Deterministic Policy만을 고려했으나, Stochastic Policy에서도 Policy Improvement Theorem은 동일하게 적용됩니다. 위의 그림은 GridWorld Environment에서 반복적으로 Policy Evaluation를 시행함으로써 Stochastic Policy에서 Optimal Policy을 찾는 과정을 보여주고 있습니다.

주어진 Environment는 모든 Action에 대해 Reward가 $R_t = -1$로 주어져 있기 때문에 최대한 빨리 출발점(왼쪽 맨위)에서 도착점(오른쪽 맨아래)에 도달하는 것이 목표입니다. 가능한 Action은 $\text{UP}$, $\text{DOWN}$, $\text{LEFT}$, $\text{RIGHT}$ 4방향이며 초기 Policy $\pi$는 모든 방향에 대해 동일한 확률 $0.25$로 Action을 선택합니다.

Policy Improvement를 위해서는 왼쪽의 State-Value Function을 토대로 Greedy하게 Policy를 선택합니다. State-Value Function은 식 (4.5)를 사용하여 계산합니다. 예를 들어, 맨 윗줄에서 왼쪽 두 번째 State를 $s_1$이라 하면, $k=1$에서의 State-Value Function $v_1$은  $v_1 (s_1) =$ $\pi (\text{RIGHT} \mid s_1) \cdot \left[-1 + 0 \right]$ $+$ $\pi (\text{LEFT} \mid s_1) \cdot \left[-1 + 0 \right]$ $+$ $\pi (\text{UP} \mid s_1) \cdot \left[-1 + 0 \right]$ $+$ $\pi (\text{DOWN} \mid s_1) \cdot \left[-1 + 0 \right]$ $= -1$ 와 같이 계산할 수 있습니다.

사실 주어진 Environment에서 State $s_1$에서 Action $\text{UP}$은 불가능하지만, 여기서는 일단 무시하고 넘어가겠습니다. 이러한 방법으로 모든 시간 단계 $k$ 마다 State-Value Function Table을 갱신할 수 있다라는 것만 이해하시면 됩니다.

Policy Iteration

Policy Iteration은 지금까지 배운 Policy Evaluation과 Policy Improvement를 반복하여 Optimal Policy를 찾는 방법입니다. 이 과정을 표현하면 아래와 같습니다.

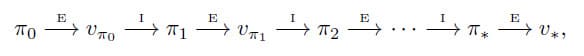
그림에서 E는 Policy Evaluation, I는 Policy Improvement를 의미합니다. Optimal Policy가 아닌 이상 새로 만들어지는 Policy는 이전의 Policy보다 확실히 우수함을 보장하며 Finite MDP에는 유한한 수의 Deterministic Policy만 있기 때문에 이 과정은 유한한 반복 횟수로 Optimal Policy와 최적의 Value Function으로 수렴되어야 합니다. Policy Iteration 알고리즘은 다음과 같습니다.

Policy Iteration에 대한 예제가 교재에 몇 개 나와있긴 하지만, 여기서는 그보다 더 간단한 예제를 통해 Policy Iteration이 Optimal Policy에 수렴하는 것을 보여드리도록 하겠습니다.

Example) State와 Action이 각각 $\mathcal{S} = \{ s_1, s_2 \}$, $\mathcal{A} (s_1) = \{ a, b \}$, $\mathcal{A} (s_2) = \{ c \}$로 주어져 있다. Action $a$는 0.5의 확률로 5의 Reward를 받고 다음 State가 $s_1$으로 되며, 0.5의 확률로 5의 Reward를 받고 다음 State가 $s_2$가 된다. Action $b$는 1의 확률로 10의 Reward를 받고 다음 State가 $s_2$가 된다. 또한 Action $c$는 1의 확률로 -1의 Reward를 받고 다음 State가 $s_2$가 된다. 이를 그림으로 표현하면 다음과 같다.

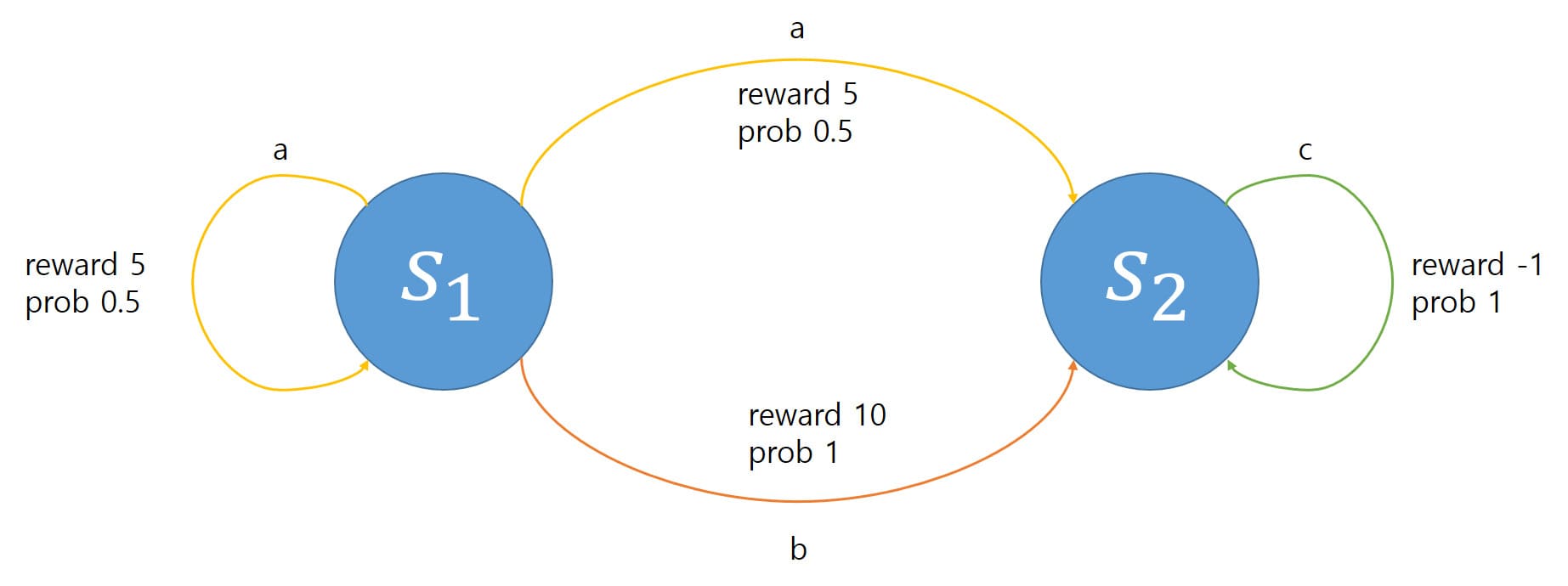
Policy Iteration에서 Discount factor $\gamma$는 0.95로 설정되어 있으며, 초기 Policy $\pi_0$는 $\pi_0 (s_1) = b$, $\pi_0 (s_2) = c$로 주어져 있다. 이를 사용하여 Optimal Policy를 찾야아 한다.

Solution)

Step 1. Policy Evaluation

\[\begin{align} v_{\pi_0} (s_1) &= 10 + 0.95 \cdot v_{\pi_0} (s_2) \\ \\ v_{\pi_0} (s_2) &= -1 + 0.95 \cdot v_{\pi_0} (s_2) \end{align}\]

두 식을 $v_{\pi_0} (s_1)$, $v_{\pi_0} (s_2)$에 대해 연립방정식을 풀면, $v_{\pi_0} (s_1) = -9$, $v_{\pi_0} (s_2) = -20$을 구할 수 있음

Step 2. Policy Improvement

\[\begin{align} \pi_1 (s_1) &= \underset{a}{\operatorname{argmax}} \left\{ 5 + 0.475 \cdot v_{\pi_0} (s_1) + 0.475 \cdot v_{\pi_0} (s_2) , 10 + 0.95 \cdot v_{\pi_0} (s_2) \right\} \\ \\ &= \underset{a}{\operatorname{argmax}} \left\{ -0.8775, -9 \right\} \end{align}\]

Policy Improvement를 통해 새로운 Policy를 계산 $\Rightarrow \pi_1 (s_1) = a, \pi_1 (s_2) = c$

Step 3. Policy Evaluation

\[\begin{align} v_{\pi_1} (s_1) &= 5 + 0.475 \cdot v_{\pi_1} (s_1) + 0.475 \cdot v_{\pi_1} (s_2) \\ \\ v_{\pi_1} (s_2) &= -1 + 0.95 \cdot v_{\pi_1} (s_2) \end{align}\]

또 다시 $v_{\pi_1} (s_1)$, $v_{\pi_1} (s_2)$에 대해 연립방정식을 풀면, $v_{\pi_1} (s_1) \approx -8.57$, $v_{\pi_1} (s_2) = -20$을 구할 수 있음

Step 4. Policy Improvement

\[\begin{align} \pi_2 (s_1) &= \underset{a}{\operatorname{argmax}} \left\{ 5 + 0.475 \cdot v_{\pi_1} (s_1) + 0.475 \cdot v_{\pi_1} (s_2) , 10 + 0.95 \cdot v_{\pi_1} (s_2) \right\} \\ \\ &= \underset{a}{\operatorname{argmax}} \left\{ -12.595, -9 \right\} \end{align}\]

Policy Improvement를 통해 새로운 Policy를 계산 $\Rightarrow \pi_2 (s_1) = a, \pi_2 (s_2) = c$

모든 State $s_1$, $s_2$에 대해 $\pi_2 (s_1) = \pi_1 (s_1)$, $\pi_2 (s_2) = \pi_1 (s_2)$가 성립하므로 Policy-stable. 따라서 Policy Iteration이 종료된다.

\[\therefore \pi_{*} (s_1) = a, \pi_{*} (s_2) = c\]

□

Value Iteration

Policy Iteration의 단점은 매 시간 단계마다 Policy Evaluation이 포함된다는 것입니다. 위에 보여드린 예제에서는 State가 단 2개였기 때문에 Policy Evaluation이 비교적 간단하였으나, 복잡한 문제에서는 이 과정 자체가 매우 오래 걸릴 수 있습니다. 만약 Policy Iteration을 무한히 반복한다면, GridWorld 예제처럼 $k=3$ 이후로 Policy가 변하지 않는데도 계속 Policy Evaluation을 수행하는 것을 볼 수 있습니다.

Policy Iteration에서의 수렴 보장을 유지하면서 Policy Evaluation 단계를 줄일 수도 있습니다. 여러 방법 중 각 State를 단 한번만 업데이트 하는 특별한 방법을 Value Iteration이라고 부릅니다. 이 때, Policy Improvement와 줄여낸 Policy Evaluation을 결합하여 다음과 같이 Value Function을 업데이트할 수 있습니다.

\[\begin{align} v_{k+1} (s) &\doteq \max_a \mathbb{E} \left[ R_{t+1} + \gamma v_k (S_{t+1}) | S_t = s , A_t = a \right] \\ \\ &= \max_a \sum_{s', r} p (s', r | s, a) \left[ r + \gamma v_k (s') \right] \tag{4.10} \end{align}\]

식 (4.10)은 모든 State $s \in \mathcal{S}$에 대해 성립하며, 수열 $\{ v_k \}$는 임의의 $v_0$에서부터 $v_{*}$로 수렴합니다.

Value Iteration을 쉽게 설명하면 단순히 Bellman Optimality Equation을 업데이트 규칙으로 바꾼 것입니다. 매 시간 단계마다 Value Iteration의 업데이트가 항상 최대값을 취해야 한다는 점을 제외하면 식 (4.5)와 매우 유사함을 알 수 있습니다. Value Iteration은 Policy Iteration과 마찬가지로 $v_{*}$에 정확히 수렴하기 위해서는 무한히 반복해야 합니다. 다만 실제 Value Iteration 알고리즘에서는 무한히 반복할 수 없기 때문에 Policy Iteration 알고리즘과 마찬가지로 종료 조건이 있습니다. Value Iteration 알고리즘에서는 Value Function의 변동이 매우 작을 때(임의의 작은 값 $\triangle$) 종료됩니다. 전체 Value Iteration 알고리즘은 다음과 같습니다.

Value Iteration은 Policy Iteration과 다르게 Evaluation과 Improvement 과정이 한번에 일어납니다. 따라서 구현 방법은 Value Iteration이 더 간단합니다. 이렇게 보면 Value Iteration이 Policy Iteration보다 우수해보이지만, 실제로는 그렇지 않습니다. Value Iteration은 각각의 단계가 짧은 대신, 그만큼 계산량이 더 많습니다. 또한 Policy 자체를 업데이트하는 Value Iteration은 Value Function을 먼저 구한 다음 Policy를 구하기 때문에 두 알고리즘을 비교했을 때 평균적으로 Policy Iteration이 더 빠르게 수렴합니다.

Value Iteration도 마찬가지로 간단한 예제를 통해 실제로 어떻게 Optimal Policy을 구할 수 있는지 알아보도록 하겠습니다. 예제는 Policy Iteration에서 사용했던 예제를 그대로 사용해서, 해결 방법만 Value Iteration으로 바꾸어 풀어보겠습니다.

Solution)

Step 1. Initialization

\[\begin{align} v_0 (s_1) &= 0 \\ \\ v_0 (s_2) &= 0 \\ \\ \triangle &= 0.1 \end{align}\]

Step 2. 1st Loop

\[\begin{align} v_1 (s_1) &= \max \left\{ 0.5 \cdot (5 + 0.95 \cdot v_0 (s_1) + 0.5 \cdot (5 + 0.95 \cdot v_0 (s_2), 10 + 0.95 \cdot v_0 (s_2) \right\} \\ \\ v_1 (s_2) &= \max \left\{ -1 + 0.95 \cdot v_0 (s_2) \right\} \\ \\ &\Rightarrow v_1 (s_1) = 10, v_1 (s_2) = -1 \end{align}\]

$v_1 (s_1) - v_0 (s_1) = 10 > 0.1 = \triangle$이므로 종료하지 않음

Step 3. 2nd Loop

\[\begin{align} v_2 (s_1) &= \max \left\{ 9.275, 9.05 \right\} \\ \\ v_2 (s_2) &= \max \left\{ -1.95 \right\} \\ \\ &\Rightarrow v_2 (s_1) = 9.275, v_2 (s_2) = -1.95 \end{align}\]

$v_2 (s_1) - v_1 (s_1) = 0.725 > 0.1 = \triangle$이므로 종료하지 않음

Step 4. 3rd Loop

\[\begin{align} v_3 (s_1) &= \max \left\{ 8.48, 8.15 \right\} \\ \\ v_3 (s_2) &= \max \left\{ -2.85 \right\} \\ \\ &\Rightarrow v_3 (s_1) = 8.48, v_3 (s_2) = -2.85 \end{align}\]

$v_3 (s_1) - v_2 (s_1) = 0.795 > 0.1 = \triangle$이므로 종료하지 않음

이런식으로 계속 Step을 밟아가며 $v_{t+1} - v_t < 0.1$이 될 때 까지 반복합니다. Step이 너무 길어져서 임의로 Step 4에서 끝났다고 가정하면, Policy를 구하는 것은 마지막 Step (여기서는 Step 4)에서 Value Function을 최대화했던 Action, 즉 $s_1$에서 $a$, $s_2$에서 c가 됩니다. 따라서 Optimal Policy는 Policy Iteration과 마찬가지로 $ \pi_{*} (s_1) = a, \pi_{*} (s_2) = c$ 입니다.

□

위의 예제에서 원래는 종료 조건을 확인할 때, $s_1$에 대한 Value Function 뿐만 아니라 $s_2$에 대한 Value Function까지 확인해야 하지만, 편의상 $s_1$만 확인하였습니다.

Asynchronous Dynamic Programming

지금까지 다루었던 DP 방법의 가장 큰 단점은 MDP의 전체 State 집합을 한번에 다룬다는 것입니다. 따라서 State 집합이 크다면 한 단계에서의 계산량이 매우 크다는 문제가 있습니다. 예를 들면 Backgammon이라는 보드게임이 있는데 (아래 그림 참고), 이 게임에는 $10^{20}$개의 State가 존재합니다. 이것을 Value Iteration으로 풀 때, 1초에 100만개의 State를 업데이트할 수 있다고 쳐도 단 한번에 Step을 완료하는데 천 년 이상이 걸립니다.

Asynchronous DP Algorithm은 State의 Value를 업데이트할 때, 이미 알고 있는 State의 Value를 사용하여 업데이트하는 방법입니다. 물론 수렴성이 보장되려면 모든 State의 Value를 업데이트해야하는 것은 같습니다.

예를 들면, Value Iteration 업데이트 식 (4.10)을 사용하여 각 단계 $k$마다 단 하나의 State $s_k$의 값만을 업데이트합니다. 물론 $v_{*}$로 수렴을 보장하려면 이것을 무한히 반복해야 합니다.

하지만 이렇게 전체 State에 대한 업데이트를 피한다고 해서 계산량이 줄어든다는 의미가 아닙니다. Asynchronous DP Algorithm의 목적은 한 단계에 너무 오래 갇히는 것을 피할 뿐입니다. 또한 이것을 응용한다면, 최적의 Action과 관련이 없는 State에 대해서는 업데이트를 줄일 수도 있는데, 이것에 대한 자세한 내용은 8장에서 다룰 예정입니다.

Asynchronous DP Algorithm의 또 다른 장점은 Agent가 MDP를 수행하는 것과 동시에 수행할 수 있다는 것입니다. 즉, Agent가 State를 방문할 때, 이것을 바로 업데이트에 적용할 수 있습니다. 추후 다룰 강화학습에서는 이렇게 Agent의 수행과 State의 Value 업데이트가 동시에 발생하는 경우가 많습니다.

Generalized Policy Iteration

Policy Iteration은 매 단계마다 Policy Evaluation과 Policy Improvement가 수행되며 Policy를 업데이트하지만, 이것이 동시에 수행되지는 않습니다. 즉, Policy Evaluation이 끝나야 Policy Improvement가 수행되고, Policy Improvement가 끝나야 다음 단계의 Policy Evaluation이 시작된다는 뜻입니다. 하지만 Asynchronous DP Algorithm처럼 꼭 이렇게 수행할 필요는 없습니다. 어차피 Policy Evaluation과 Policy Improvement를 계속 수행하기만 하면 언젠가 최적의 Policy에 도달하기 때문입니다.

Generalized Policy Iteration (GPI)는 Policy Evaluation과 Policy Improvement가 상호 작용하도록 하는 일반적인 개념을 말합니다. 즉, Policy는 항상 Value Function에 의해 개선되고, Policy로부터 항상 Value Function이 계산됩니다. Evalution과 Improvement가 모두 안정화된다면 Value Function과 Policy가 최적이라는 뜻입니다. 이 때 Bellman Optimality Equation이 성립하기 때문입니다. 대부분의 강화학습은 GPI 관점에서 잘 설명할 수 있습니다.

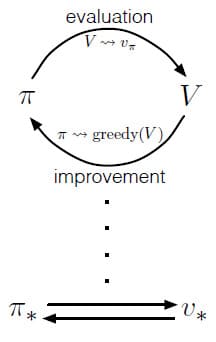
GPI의 Evaluation과 Improvement 과정은 여러 가지 관점에서 볼 수 있습니다. 예를 들어, Value Function으로 Policy를 greedy하게 만드는 것은 변경된 Policy로 인해 Value Function을 틀리게 만들고, Value Function과 Policy을 일관되게 만들면 Policy가 greedy하지 않는 문제가 생깁니다. 하지만 장기적으로 두 과정은 최적의 Value Function과 최적의 Policy를 찾기 위해 상호 작용하기 때문에, 경쟁과 협력 관계로 볼 수 있습니다.

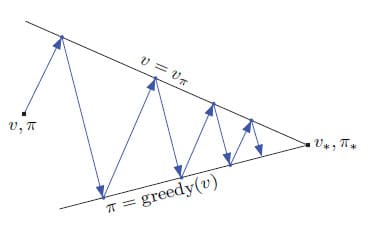
또 다른 관점으로는 두 가지 제약 조건, 또는 목표라고 볼 수도 있습니다. 위의 그림은 이 관계를 대략적으로 도식화한 모습인데, Evaluation과 Improvement의 각 과정은 서로의 목표에 도달할 수 있는 하나의 솔루션을 도출합니다. (Value Function을 통해 조금 더 최적의 Policy를 유도하며, 그 반대도 성립) 그림의 화살표를 따라가다보면 하나의 목표를 향하게 될 때 다른 하나의 목표는 멀어지게 됩니다. 하지만 두 과정의 목표는 결국 하나로 이어지기 때문에 결국에는 두 과정의 목표가 함께 달성됩니다.

Efficiency of Dynamic Programming

지금까지 배운 DP는 다른 방법들과 비교했을 때 매우 효율적입니다. 물론 State의 수 $n$과 Action의 수 $k$가 매우 크다면 그렇지 않을 수 있지만, 일반적인 상황에서 DP는 (Deterministic) Policy의 수가 $k^n$개인 경우라도 다항식 시간에 Optimal Policy를 찾는 것이 보장됩니다. Linear Programming 방법과 비교해 봤을 때, 최악의 경우 수렴에 대한 보장이 DP 방법보다 낫다는 장점이 있지만, State의 수가 적을 때 약 100배나 비효율적입니다. 게다가 정 반대로 State가 매우 많은 상황에서는 DP 방법만 가능하다는 문제도 있습니다.

DP 방법의 단점으로 계속 수많은 State에서 계산이 어렵다는 점을 지적해왔으나(Curse of Dimensionality), 현재 컴퓨터의 수준으로 수백만 개의 State 정도는 DP 방법으로 해결이 가능합니다. 많은 문제가 Policy Iteration과 Value Iteration으로 해결되고 있으며 보통 초기 Value나 Policy를 예제처럼 완전 무작위로 설정하지 않고 어느 정도 최적에 가깝게 주어지기 때문에 이론상 최악의 실행 시간보다 빠르게 수렴합니다.

매우 큰 State 집합의 문제에서는 마지막으로 다루었던 Asynchronous DP Algorithm이 선호됩니다. 동기식 방법은 한 Step 마다 모든 State에 대한 계산과, 저장할 메모리가 필요하기 때문에 비효율적이기 때문입니다. Asynchronous DP Algorithm 외에도 계산량과 메모리의 낭비를 줄이기 위해 GPI를 변형하는 방법도 연구되고 있습니다.

Summary

이번 장에서는 Finite MDP를 풀기 위해 Dynamic Programming의 기본 아이디어와 알고리즘을 익혔습니다. Policy Evaluation은 주어진 Policy로 반복적인 계산을 통해 Value Function을 계산합니다. Policy Improvement는 Policy Evaluation으로 구한 Value Function을 이용하여 개선된 Policy를 계산합니다. 이 두 가지 절차를 반복하거나, 혼합하는 방식으로 DP의 핵심 알고리즘인 Policy Iteration과 Value Iteration을 얻을 수 있습니다. 이 두 방법은 MDP에 대한 완전한 지식이 주어졌을 때, Optimal Policy 및 Value Function을 계산할 수 있습니다.

이러한 DP 방법은 매 Step마다 모든 State 집합에 대해 업데이트 작업을 수행합니다. (이것을 Sweep이라고 부릅니다) 이러한 작업은 Bellman Optimality Equation을 이용하여 가능한 모든 후속 State의 Value와 전이 확률을 기반으로 업데이트합니다. 업데이트 후 더 이상 변경되는 값이 없다면 수렴했다고 볼 수 있습니다.

DP 방법을 포함하여 대부분의 강화학습 방법에 대한 기본 아이디어는 Generalized Policy Iteration (GPI)의 개념에서 얻을 수 있습니다. GPI는 근사적인 Policy과 근사적인 Value Function 사이의 상호 작용 프로세스에 대한 일반적인 개념입니다. 주어진 Policy를 토대로 Value Function을 Policy에 대한 실제 Value Function과 유사하게 맞추는 프로세스와, 주어진 Value Function을 토대로 현재 Policy보다 더 나은 Policy로 변경하는 프로세스가 같이 일어납니다. 이번 장에서 다룬 DP 방법은 GPI가 Optimal Policy와 Value Function에 수렴하는 것이 보장되어 있지만, 모든 GPI가 그러한 것은 아닙니다.

또한 DP에서 매 Step 마다 모든 State 집합을 한번에 업데이트할 필요는 없습니다. Asynchronous DP Algorithm은 이미 구한 State의 정보를 토대로 새로운 State를 업데이트 함으로써 일부분의 State만 업데이트 하는 방식입니다. Asynchronous DP Algorithm라고 해도 결국 모든 State를 업데이트 해야하는 것은 동일하지만, DP 알고리즘이 지나치게 오랜 시간동안 한 Step에 머무는 것을 방지해줍니다.

마지막으로 DP 방법은 모두 이어지는 State의 추정 Value를 기반으로 State의 추정 Value를 업데이트합니다. 즉, 다른 추정치를 기반으로 현재의 추정치를 업데이트합니다. 이것을 Bootstrapping이라고 부릅니다. 이번 장에서는 Environment에 대한 Model이 정확하게 주어진 상황에서 Bootstrapping을 수행하였지만,  그렇지 않은 경우에도 Bootstrapping을 사용할 수 있습니다. 우선 다음 장에서는 Environment에 대한 Model이 주어지지 않은 상황에서 Bootstrapping을 사용하지 않는 강화학습 방법을 먼저 소개하도록 하겠습니다.

4장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!