Finite Markov Decision Processes

이번 장에서는 이 책에서 해결하고자 하는 목표인 Finite Markov Decision Processes (Finite MDP)에 대해 소개합니다. $k$-armed bandit 문제에서는 즉각적인 Reward에 대한 피드백만 고려하였으나, MDP는 즉각적인 Reward와 더불어 이어지는 State와 미래에 받을 Reward 등을 모두 포함한 의사 결정이 필요합니다. 수식으로 표현하면 bandit 문제에서는 각각의 Action $a$에 대하여 $q_* (a)$를 추정하였으나, MDP에서는 각각의 State $s$와 Action $a$를 모두 포함한 $q_* (s, a)$를 추정하거나, State $s$에 대한 Value $v_* (s)$를 추정합니다.

MDP는 강화학습 문제를 이론적으로 접근하기 위해 수학적으로 표현된 형태입니다. MDP에서 핵심적으로 다루게 될 요소는 Return, Value Function, Bellman Equation입니다. 그리고 여기서는 Finite MDP에만 한정하여 접근할 예정입니다.

The Agent–Environment Interface

MDP는 목표를 달성하기 위해 상호 작용을 통해 학습하는 문제의 간단한 프레임을 의미합니다. 의사결정을 통해 학습을 하는 주체를 Agent로 정의하고, Agent가 상호작용하는 모든 외부적인 것들을 Environment라고 합니다. Agent가 Action을 선택하고 수행하면 Environment로부터 Reward를 제공받습니다.

시간은 $t = 0, 1, 2, … $와 같이 이산적으로 주어지며, 각 시간 단계 $t$에서 Agent는 Environment에 포함된 State $S_t$를 인지하고 이를 기반으로 Action $A_t$를 선택합니다. 그로부터 Agent는 Environment으로부터 Reward $R_{t+1} \in \mathbb{R}$를 받고 다음 State $S_{t+1}$에 도달합니다. 이 과정을 아래와 같이 나열한 것을 Sequence 또는 Trajectory라고 부릅니다.

\[S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, ... \tag{3.1}\]

또한 이것을 그림으로 표현하면 다음과 같습니다. 강화학습을 다루는 논문에는 이것과 비슷한 그림이 들어가는 경우가 많으니 참고해주시기 바랍니다.

Finite MDP에서 State set $\mathcal{S}$, Action set $\mathcal{A}$, Reward set $\mathcal{R}$은 모두 유한집합입니다. 이 때, 확률변수 $R_t$와 $S_t$는 이전 State와 Action에 따른 이산 확률 분포가 됩니다. 이것을 확률적으로 표현하면 다음과 같습니다.

\[p(s', r | s, a) \doteq Pr \left\{ S_t = s', R_t = r | S_{t-1} = s, A_{t-1} = a \right\} \tag{3.2}\]

함수 $p$는 MDP의 Dynamics를 정의합니다. 식 (3.2)의 오른쪽 항을 해석하면 $t-1$ 시간의 State가 $s$이고 Action이 $a$일 때, 다음 시간 $t$에서의 State가 $s’$, Reward가 $r$일 확률이라는 뜻이 됩니다. 중간의 $\mid$는 조건부 확률이라는 의미입니다. 확률이기 때문에 다음과 같이 모든 State와 Action에 대해서 확률의 합이 1이 나와야 합니다.

\[\sum_{s' \in \mathcal{S}} \sum_{r \in \mathcal{R}} p(s', r | s, a) = 1, \quad \text{for all } s \in \mathcal{S}, a \in \mathcal{A} (s) \tag{3.3}\]

MDP에서 특이한 점은 현재의 State와 Reward는 오직 직전의 State와 Action에만 영향을 받는다는 것입니다. 실제 확률식을 보더라도 조건으로 걸린 부분은 직전 State $S_{t-1}$와 Action $A_{t-1}$ 뿐입니다. 다시 말해서, 그보다 이전에 발생했던 State와 ACtion에는 전혀 영향받지 않는다는 뜻입니다. 이것을 Markov Property라고 합니다. 이 책에서 다루는 강화학습은 모두 Markov Property를 가정하고 있습니다.

방금 소개한 확률식은 다양한 변형이 가능합니다. 먼저 Reward $r$을 제외한다면 다음과 같이 쓸 수도 있습니다.

\[\begin{align} p(s' | s, a) & \doteq Pr \left\{ S_t = s' | S_{t-1} = s, A_{t-1} = a \right\} \\ \\ &= \sum_{r \in \mathcal{R}} p(s', r | s, a) \tag{3.4} \end{align}\]

또는 다음과 같이 Reward를 State와 Action으로 표현한 식도 있습니다.

\[\begin{align} r(s, a) & \doteq \mathbb{E} \left[ R_t | S_{t-1} = s, A_{t-1} = a \right] \\ \\ &= \sum_{r \in \mathcal{R}} r \sum_{s \in \mathcal{S}} p(s', r | s, a) \tag{3.5} \end{align}\]

마지막으로 Reward를 이전 State와 Action, 다음 State로 표현할 수도 있습니다.

\[\begin{align} r(s, a, s') & \doteq \mathbb{E} \left[ R_t | S_{t-1} = s, A_{t-1} = a, S_t = s' \right] \\ \\ &= \sum_{r \in \mathcal{R}} \frac{p(s', r | s, a)}{p(s'| s, a)} \tag{3.6} \end{align}\]

이렇게 여러 표현이 존재하지만, 이 책에서는 식 (3.2)와 같은 표현을 주로 사용할 예정입니다.

Goals and Rewards

강화학습에서 Agent의 목표는 Environment으로부터 주어지는 Reward의 총합을 최대화하는 것으로 정의할 수 있습니다. 각 시간 단계에서의 Reward는 $R_t \in \mathbb{R}$로 정의합니다. 하지만 Agent는 즉각적인 Reward $R_t$가 아니라 장기적으로 받을 수 있는 누적 Reward를 극대화해야 합니다. 교재에서는 이것을 다음과 같이 말하고 있습니다.

That all of what we mean by goals and purposes can be well thought of as the maximization of the expected value of the cumulative sum of a received scalar signal (called reward).

Reward는 Agent의 목표를 공식화하는데 사용합니다. 예를 들면 미로를 탈출하는 최단 경로를 찾을 때 모든 시간 단계에 -1의 Reward를 주고, 목적지에 도달하면 10의 Reward을 주는 방식으로 설계하여 최대한 빨리 미로를 탈출하게 만들 수 있습니다.

하지만 이것이 Agent에게 사전 지식을 전달하는 역할은 아닙니다. 바둑을 예로 들면 축을 만들거나 돌을 딴다고 해서 Reward를 주는 것이 아니라, 게임에서 승리해야 Reward를 주는 방식으로 설계해야 합니다. 즉, 하위 목표를 따로 설계하는 것이 아닙니다.

Returns and Episodes

직전 부분에서 Agent의 목표는 장기적으로 받는 누적 Reward를 극대화하는 것이라고 정의했습니다. 이번에는 이것을 구체적으로 정의해보겠습니다. 먼저 시간 단계 $t$ 이후로 받은 Reward를 순서대로 $R_{t+1}, R_{t+2}, R_{t+3}, …$로 표현하도록 하겠습니다. Agent가 시간 단계 $t$ 이후부터 마지막 시간 단계인 $T$까지 받을 수 있는 기대 이익를 $G_t$라고 정의하면, $G_t$는 다음과 같이 Reward의 합으로 정의할 수 있습니다. $G_t$는 Return이라고 부릅니다.

\[G_t \doteq R_{t+1} + R_{t+2} + R_{t+3} + \cdots + R_{T} \tag{3.7}\]

이러한 정의는 마지막 시간 단계라는 개념이 있는 상황에서만 의미가 있습니다. 예를 들어 위에서 언급한 미로 탈출 문제에서는 목적지에 도달하면 끝나기 때문에 마지막 시간 단계가 존재합니다. 이렇게 처음부터 끝까지 Agent와 Environment의 상호작용을 마치는 것을 하나의 Episode라 부릅니다. 각 Episode는 독립적이며 게임의 승리/패배와 같이 서로 다른 Reward를 받을 수도 있습니다. 이러한 Episode에서 마지막 State는 $\mathcal{S}$로 표현한 일반적인 State와 구분짓기 위해 $\mathcal{S^+}$로 표현합니다. 또한 이렇게 Episode로 이루어진 문제를 Episodic Task라고 부릅니다. 각각의 Episode마다 마지막 State에 도달하는 시간이 차이가 날 수 있기 때문에 마지막 시간 단계 $T$는 Random Variable (확률 변수)입니다.

하지만 모든 문제들이 Episode를 갖고 있는 것은 아닙니다. 끊임없이 프로세스를 할당하는 작업 관리자처럼 마지막 시간 단계라는 것이 존재하지 않고 무한히 이어지는 문제도 많습니다. 이러한 문제들을 Continuing Task이라고 부릅니다. Continuing Task에서 식 (3.7)을 그대로 사용한다면 Return $G_t$가 무한대가 될 가능성이 크다는 문제가 있습니다.

이 때 사용되는 개념이 Discounting입니다. 이것은 미래에 받는 Reward을 일정 비율로 줄임으로써 현재로부터 멀어질수록 Reward에 대한 Value를 낮추는 방법입니다. 이것을 Discounted Return이라고 정의하며 다음과 같이 표현됩니다.

\[G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \tag{3.8}\]

위 식에서 $0 \le \gamma \le 1$은 Discount Rate라고 부릅니다. Discount Rate는 미래에 받을 Reward가 현재에 얼마나 Value가 있는지 판단하는 기준입니다. 만약 $k$ 시간 단계 후에 받을 Reward를 지금 당장 받는다면 $\gamma^{k-1}$ 배의 Value가 있습니다. 만일 $\gamma = 0$인 경우에는 눈앞에 있는 Reward만을 최대화하는 근시적 판단을 하게 되고, $\gamma$가 1에 가까워질수록 미래의 Reward를 더 많이 반영하게 됩니다.

식 (3.8)은 다음과 같이 표현할 수도 있습니다. 이렇게 변경한 식은 Continuing Task가 아니라도 사용할 수 있습니다.

\[\begin{align} G_t &\doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \\ \\ &= R_{t+1} + \gamma \left( R_{t+2} + \gamma R_{t+3} \cdots \right) \\ \\ &= R_{t+1} + \gamma G_{t+1} \tag{3.9} \end{align}\]

식 (3.8)은 항의 개수가 무한대지만, $\gamma < 1$이고 Reward가 0이 아닌 상수라면 그 합은 유한합니다. 예를 들어, Reward가 1이라면 다음과 같이 간단하게 정리할 수 있습니다.

\[G_t = \sum_{k=0}^{\infty} \gamma^k = \frac{1}{1 - \gamma} \tag{3.10}\]

Unified Notation for Episodic and Continuing Tasks

지금까지 강화학습에서 사용되는 Return $G_t$를 Episodic Task의 경우와 Continuing Task의 경우로 나누어 다루었습니다. 이번에는 두 경우 모두 사용할 수 있는 통일된 표기법을 소개하도록 하겠습니다.

먼저 Episodic Task를 고려해보면, 각각의 Episode를 구분해야하고 Episode별 시간 단계 또한 구분해야 합니다. 따라서 원래는 Episode 숫자와 시간 단계 숫자가 모두 표기된 $S_{t, i}$와 같은 표기 방식이 필요하지만($i$는 에피소드 숫자), 여기서는 보통 특정 Episode를 고려하거나 모든 Episode에 해당하는 것들을 다루기 때문에 이러한 명시적인 표기를 사용하지 않고, 그냥 $S_t$를 사용하기로 합니다.

다음은 Return에 대한 표기입니다. 이전에는 Episodic Task에서 식 (3.7)로 표기하였고 Continuing Task에서는 식 (3.8)로 표기하였습니다. 이것은 Episodic Task를 Continuing Task와 같은 식으로 바꾸는 것으로 해결할 수 있습니다. 아래 그림과 같이 Episodic Task가 끝난 이후로는 모든 Reward를 0으로 정의하고 같은 State에 반복적으로 돌아오게 설계하면 됩니다.

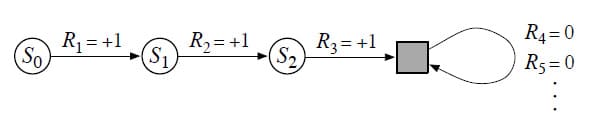
위의 State Diagram에서 마지막 사각형은 Episode의 끝을 나타내며, 이를 Absorbing State라고 부릅니다. 위의 예제에서 모든 Reward를 합쳐도 $R_4$ 이후로는 Reward가 0이기 때문에 $R_1$, $R_2$, $R_3$을 더한 값과 동일합니다. Discounting을 포함해도 마찬가지입니다. 이로써 다음과 같이 Return $G_t$를 통합하여 표기할 수 있습니다.

\[G_t \doteq \sum_{k=t+1}^T \gamma^{k-t-1} \tag{3.11}\]

식 (3.11)은 $T = 1$ 또는 $T = \infty$도 상관없이 유효합니다. 이 책의 나머지 부분에서는 이렇게 표기를 단순화함으로써 Episodic Task나 Continuing Task를 구분하지 않고 문제를 다루도록 하겠습니다.

Policies and Value Functions

대부분의 강화학습 알고리즘은 Agent가 주어진 State에 있는 것이 얼마나 좋은지(또는 주어진 State에서 특정 Action을 수행하는 것이 얼마나 좋은지)를 추정하는 Value Function을 가지고 있습니다. 여기서 얼마나 좋은가를 판단하는 기준은 받을 수 있는 미래의 Reward, 즉 총 Reward의 기대값으로 정의됩니다. 이 때의 기대값은 어떤 Action을 선택하는지에 따라 다르며, Value Function은 Policy를 기반으로 정의됩니다.

Policy은 각 State에서 각각의 Action을 선택할 확률로 정의됩니다. Agent가 시간 $t$에서 Policy $\pi$를 따르는 경우 $\pi (a \mid s)$는 State $S_t = s$일 때 $A_t = a$일 확률입니다. Policy $\pi$는 강화학습이 진행되는 동안 계속 업데이트됩니다.

Value Function은 State $s$에서 Policy $\pi$를 따를 때 예상되는 Return을 의미합니다. Value Function는 $v_{\pi} (s)$로 표기하며 다음과 같이 정의할 수 있습니다.

\[\begin{align} v_{\pi} (s) & \doteq \mathbb{E}_{\pi} \left[ G_t | S_t = s \right] \\ \\ &= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg| S_t = s \right], \text{ for all } s \in \mathcal{S} \tag{3.12} \end{align}\]

$v_{\pi} (s)$는 Policy $\pi$에 대한 State-Value Function이라고 부릅니다. State-Value Function과는 다르게 State 뿐만 아니라 Action을 포함한 Value Function도 있습니다. State와 Action을 모두 고려하는 Value Function을 Action-Value Function이라고 부르고, 이를 $q_{\pi} (s, a)$으로 표현합니다. $q_{\pi} (s, a)$는 다음과 같이 정의합니다.

\[\begin{align} q_{\pi} (s, a) & \doteq \mathbb{E}_{\pi} \left[ G_t | S_t = s , A_t = a \right] \\ \\ &= \mathbb{E}_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \bigg| S_t = s , A_t = a \right] \tag{3.13} \end{align}\]

Value Function $v_{\pi} (s)$와 $q_{\pi} (s, a)$는 경험을 통해 추정할 수 있습니다. 예를 들어, Agent가 Policy $\pi$를 따를 때 발생하는 각각의 State에 대해 실제 얻게 되는 Reward의 평균을 구하게 되면 실제 $v_{\pi} (s)$ 값에 수렴하게 됩니다. $q_{\pi} (s, a)$도 이와 마찬가지로 각 State에 대해 특정 Action을 선택했을 때 받는 Reward의 평균을 계산하면 됩니다. 이러한 방법을 Monte Carlo Method이라고 합니다. Monte Carlo Method는 많은 무작위 샘플을 구한 다음 그것들의 평균을 계산하는 방법입니다. Monte Carlo Method에 대한 구체적인 내용은 5장에서 다룰 예정입니다.

그러나 State와 Action이 매우 많은 경우 그만큼 Sample이 많이 필요하게 되고, 어지간한 수의 Sample로는 평균이 정확한 값에 수렴하지 않을 수도 있습니다. 이 때는 Value Function를 매개 변수들로 표현하고 Sample에 맞게 함수 자체를 추정하는 방법을 사용합니다. 이것은 9장 이후로 다룰 예정입니다.

강화학습은 4장에서 다룰 Dynamic Programming과 매우 밀접한 관련이 있는데, Value Function 또한 Dynamic Programming처럼 표현할 수 있습니다. 식 (3.9)와 연관되어 모든 Policy $\pi$ 및 모든 State $s$에 대해, 다음 관계가 성립합니다.

\[\begin{align} v_{\pi} (s) & \doteq \mathbb{E}_{\pi} \left[ G_t | S_t = s \right] \\ \\ &= \mathbb{E}_{\pi} \left[ R_{t+1} + \gamma G_{t+1} | S_t = s \right] \tag{by 3.9} \\ \\ &= \sum_{a} \pi (a | s) \sum_{s'} \sum_{r} p ( s' , r | s, a ) \left[ r + \gamma \mathbb{E}_{\pi} [ G_{t+1} | S_{t+1} = s' ] \right] \\ \\ &= \sum_{a} \pi (a | s) \sum_{s', r} p ( s' , r | s, a ) \left[ r + \gamma v_{\pi} (s') \right], \quad \text{for all } s \in \mathcal{S} \tag{3.14} \end{align}\]

식 (3.14)를 $v_{\pi}$에 대한 Bellman Equation이라고 합니다. Bellman Equation은 현재 State의 Value와 이어지는 State의 Value 사이의 관계를 표현합니다. 아래에 있는 Backup Diagram을 보시면 현재 State $s$에서 이어질 수 있는 모든 후속 State $s’$을 고려하는 것을 알 수 있습니다. 앞에서 말씀드렸듯이 Policy $\pi$는 Action을 선택할 확률을 의미하기 때문에, 각 Action을 선택했을 때 받을 수 있는 Reward에 확률 가중치를 포함한 평균을 계산하게 됩니다.

Value Function $v_{\pi}$는 Bellman Equation에 대한 유일한 해법입니다. 4장에서 Bellman Equation이 어떻게 $v_{\pi}$를 계산하고, 근사화하고, 학습하는지를 자세하게 다룰 예정입니다.

Optimal Policies and Optimal Value Functions

강화학습 문제를 해결한다는 것은 장기적인 관점에서 최대의 보상을 얻을 수 있는 Policy를 찾는다는 것과 동일한 의미입니다. 먼저 두 개의 Policy가 존재할 때, 어떤 Policy가 더 좋은가를 판단하는 방법부터 알아보도록 하겠습니다. Finite MDP에서, Policy $\pi$가 Policy $\pi^{\prime}$보다 좋다는 것은(즉, $\pi \ge \pi^{\prime}$) 모든 State $s \in \mathcal{S}$에 대해 Value Function $v_{\pi}$가 작지 않다는 것입니다. (즉, $v_{\pi} (s) \ge v_{\pi^{\prime}}$) Finite MDP에서는 항상 다른 모든 Policy보다 좋거나 같은 Policy가 하나 이상 존재하는데, 이것을 Optimal Policy라고 부릅니다. 최적의 Policy가 여러 개 존재할 수도 있지만, 어차피 동일하기 때문에 모두 $\pi_{*}$라고 표기합니다. 또한 이 때의 State-Value Function를 Optimal State-Value Function이라고 부르고, $v_{*}$로 표기하며, 다음과 같이 정의합니다.

\[v_{*} (s) \doteq \max_{\pi} v_{\pi} (s) \quad \text{for all } s \in \mathcal{S} \tag{3.15}\]

마찬가지로, Optimal Action-Value Function는 $q_{*}$로 표기하며, 다음과 같이 정의합니다.

\[q_{*} (s, a) \doteq \max_{\pi} q_{\pi} (s, a) \quad \text{for all } s \in \mathcal{S} \text{ and } a \in \mathcal{A} (s) \tag{3.16}\]

최적의 Policy를 따르는 $q_{*}$에서 예상되는 Reward는 다음과 같이 표현할 수 있습니다.

\[q_{*} (s, a) = \mathbb{E} \left[ R_{t+1} + \gamma v_{*} ( S_{t+1} ) | S_t = s, A_t = a \right] \tag{3.17}\]

$v_{*}$는 Policy에 대한 Value Function이기 때문에 식 (3.14)의 Bellman Equation에 의해 주어진 Self-Consistency 조건을 만족해야 합니다. 즉, Bellman Equation에서 최적의 Policy를 따른다는 것은 $v_{*}$에 대한 Bellman Equation이 Bellman Optimality Equation이 된다는 것을 의미합니다. 따라서 Bellman Optimality Equation에서의 Value Function는 각 State에서 최적의 Action을 수행한다는 것이며, 그 결과로 최대의 Reward를 받아야 합니다. 이것을 수식으로 전개하면 다음과 같습니다.

\[\begin{align} v_{*} (s) &= \max_{a \in \mathcal(A) (s)} q_{\pi_*} (s, a) = \max_a \mathbb{E}_{\pi_*} \left[ G_t | S_t = s, A_t = a \right] \\ \\ &= \max_a \mathbb{E}_{\pi_*} \left[ R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a \right] \tag{by (3.9)} \\ \\ &= \max_a \mathbb{E} \left[ R_{t+1} + \gamma v_{*} (S_{t+1}) | S_t = s, A_t = a \right]\tag{3.18} \\ \\ &= \max_a \sum_{s', r} p ( s', r | s, a ) \left[ r + \gamma v_{*} (s') \right] \tag{3.19} \end{align}\]

식 (3.18)과 (3.19)는 $v_{*}$에 대한 Bellman Optimality Equation의 두 가지 형태입니다. $q_{*}$에 대한 Bellman Optimality Equation은 다음과 같습니다.

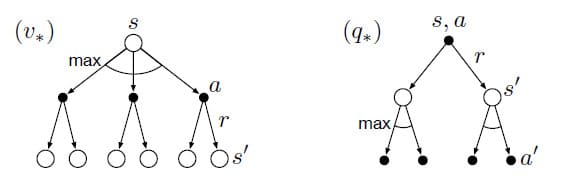
\[\begin{align} q_{*} (s, a) &= \mathbb{E} \left[ R_{t+1} + \gamma \max_{a'} q_{*} (S_{t+1}, a') \bigg| S_t = s, A_t = a \right] \\ \\ &= \sum{s', r} p (s', r | s, a) \left[ r + \gamma \max_{a'} q_{*} (s', a') \right] \tag{3.20} \end{align}\]

아래 그림은 $v_{*}$와 $q_{*}$에 대한 Bellman Optimality Equation에서 고려되는 미래의 State와 Action의 범위를 표현한 Backup Diagram입니다. 왼쪽은 식 (3.19)를 표현한 그림이고, 오른쪽은 식 (3.20)을 표현한 그림입니다.

Finite MDP에서 $v_{*}$에 대한 Bellman Optimality Equation에는 고유한 해법이 있습니다. Bellman Optimality Equation에서는 각각의 State에 대해 하나의 방정식이 있는 구조이기 때문에, $n$개의 State가 있으면 $n$개의 미지수가 있는 $n$개의 방정식이 나옵니다. 만약 Environment에서 $p$를 알 수 있다면 Nonlinear Equation을 품으로써 $v_{*}$를 구할 수 있습니다. (ex. Newton-Raphson Method) 같은 이유로 $q_{*}$도 마찬가지입니다.

$v_{*}$를 구한 이후, 각각의 State에서 Bellman Optimality Equation에서 최대값을 얻는 하나 이상의 Action을 찾습니다. 이런 Action에만 0이 아닌 확률을 할당하는 Policy이 바로 최적의 Policy입니다. $q_{*}$를 구했다면 최적의 Policy을 찾기 더 쉽습니다. 모든 State $s$에 대해 $q_{*}(s, a)$를 최대화하는 Action을 선택하면 됩니다.

하지만 Bellman Optimality Equation을 푸는 것으로 강화학습 문제를 해결하는 것은 사실 유용한 방법이 아닙니다. Bellman Optimality Equation을 풀기 위해서는 (1) Environment가 정확하게 알려져 있고, (2) 계산하기 위한 자원이 충분해야 하며, (3) Markov Property를 갖고 있어야 한다는 3가지 조건이 필요합니다. 하지만 대부분의 문제에서는 이 3가지 조건을 모두 갖고있지 않습니다. Environment가 정확하게 알려져있는 문제는 사실상 인위적으로 만든 문제들 뿐이고, 최신 슈퍼 컴퓨터로도 간단한 문제의 Bellman Equation을 푸는데 굉장히 오랜 시간이 걸리는데다 대부분의 문제에서 Markov Property를 갖고있다는 증명을 하기가 어렵기 때문입니다. 따라서 대부분의 강화학습 문제에서는 근사적인 솔루션으로 해결하는 수밖에 없습니다. 근사적인 솔루션 중 대표적인 방법이 바로 Dyanmic Programming 방법인데, 다음 장에서 어떤 방법으로 해결하는지 더 자세히 다룰 예정입니다.

Optimality and Approximation

지금까지 최적의 Value Function와 최적의 Policy을 정의했습니다. 하지만 Bellman Optimality Equation을 통해 최적의 Policy을 찾는 방법은 매우 많은 계산량으로 인해 실제 문제에서는 사용하기 어려운 방법입니다. 근사적인 솔루션으로 접근해도 Value Function나 Policy, 그리고 Model의 근사치를 구축하기 위해서는 많은 크기의 메모리가 필요합니다. State과 Action의 집합이 작은 경우에는 행과 열을 State/Action으로 정의하여 표로 나타낼 수 있지만, State와 Action이 엄청나게 많은 경우에는 매개변수화하여 함수 자체를 근사해야할 수도 있습니다.

이러한 근사적인 접근에서 가장 중요한 것은 기회를 최소한으로 낭비함으로써 최적의 Action을 찾는 것입니다. 쉽게 표현하면 지금 당장 보이는 가장 좋은 Action을 고를 수도 있지만, 내가 선택해보지 않은 Action이 장기적으로 봤을 때 더 좋은 Reward를 제공할 수 있으므로 선택해봐야할 수도 있습니다. 이 경우 높은 Reward를 제공하면 기회를 낭비한 것이 아니지만, 생각한 것과 다르게 실제로도 낮은 Reward를 제공하는 Action이었다면 그 기회를 낭비한 것이 됩니다. 앞으로 많은 강화학습 방법에서는 최적의 Policy을 근사화하기 위해 기회를 최소한으로 낭비하는 많은 노력들을 다룰 예정입니다.

Summary

3장은 꽤 많은 내용을 다뤘습니다. 배운 내용을 요약해보면 강화학습은 Environment와의 상호 작용을 통해 목표를 달성하기 위한 방법을 배우는 것입니다. Agent는 매 시간 State를 마주하고, 해당 State에서 어떤 Action을 선택할 것인지 결정합니다. Agent의 Action에 따라 Environment는 Agent에게 Reward를 제공합니다. 강화학습의 목적은 이러한 구조에서 최대의 누적 Reward를 받기 위한 방법인 Policy를 구하는 것입니다.

이러한 강화학습을 수식화한 것이 Markov Decision Process (MDP)입니다. 특히 여기서는 유한개의 State, 유한개의 Action과 유한개의 Reward가 있는 Finite MDP에 집중합니다. 강화학습에서의 대부분의 이론은 Finite MDP에만 제한적으로 적용되기 때문입니다.

Return은 Agent가 최대화하려는 미래의 Reward를 나타냅니다. 강화학습 환경에서 끝이 존재하는 Episodic Task는 Reward의 합으로 간단하게 표현이 가능하지만, Continuing Task는 Reward의 합이 무한대일 수도 있기 때문에 Reward에 보정값이 필요합니다. 이 때, 받게 되는 Reward가 현재로부터 멀어질수록 작아지는 가중치를 곱해주는데, 이것을 Discounting라고 합니다.

Policy의 Value Function $v_{\pi}$와 $q_{\pi}$는 Agent가 Policy $\pi$를 사용할 때 State, 또는 State-Action 쌍에서 예상되는 수익을 나타냅니다. 최적의 Value Function은 최적의 Policy를 사용했을 때 받을 수 있는 총 Reward의 기대값입니다. 최적의 Value Function는 고유하지만, 최적의 Policy는 여러 개가 있을 수도 있습니다. Bellman Optimality Equation은 최적의 Value Function을 계산하고 이를 통해 최적의 Policy를 구할 수도 있습니다. 하지만 계산량과 같은 현실적인 문제로 인해 대부분 문제에서 Bellman Optimality Equation으로 직접 강화학습 문제를 해결하지는 못합니다.

따라서 강화학습 문제는 앞으로 근사적인 방법을 사용하여 접근할 예정입니다. 안타깝게도 강화학습에서 완벽한 최적의 솔루션을 찾을 수 없지만, 어떻게 최적의 솔루션에 가깝게 근사할 수 있는지를 다양한 한 시도를 통해 알아볼 것입니다.

3장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!