Monte Carlo Methods

이번 장에서는 지난 장과 마찬가지로 Value Function을 추정하고 Optimal Policy를 찾기 위한 방법을 다루지만, 지난 장과는 달리 MDP에 대한 완전한 정보를 알고 있다고 가정하지 않습니다. Monte Carlo Method는 Environment와의 상호 작용을 통해 얻은 경험을 기반으로 Optimal Policy를 찾는 방법입니다. 이 때 Environment와의 상호작용은 실제로 이루어지는 경험 뿐만이 아니라 시뮬레이션된 경험이라도 상관 없습니다.

3장에서 MDP를 끝이 존재하는 Episodic Task와 끝이 없는 Continuing Task로 분류하였는데, 이번 장에서는 일단 Episodic Task 상황만 가정하도록 하겠습니다. Monte Carlo Method 또한 지난 장에서 배운 Generalized Policy Iteration (GPI)의 아이디어를 기반으로 하지만, 그 때와 달리 MDP에서 직접 Value Function을 계산하지 않고 Sample로부터 Value Function을 계산합니다. 물론 여전히 그 때처럼 Optimal Value Function에 수렴하기 위해 상호작용하는 것은 같습니다.

Monte Carlo Prediction

가장 먼저 Policy가 주어졌을 때 State-Value Function을 학습하기 위해 Monte Carlo Method를 고려해보겠습니다. State의 Value는 해당 State에서 시작했을 때 얻을 수 있는 기대 수익이므로, 경험으로 이를 추정하기 위해서는 해당 State를 여러 번 방문한 후 얻은 수익의 평균을 구하면 됩니다. 당연히 많이 방문할수록 평균값이 정확한 State의 Value에 가까워집니다. 이것이 바로 Monte Carlo 방법의 기본 아이디어입니다.

Monte Carlo Method는 두 가지 방법으로 나눌 수 있습니다. 만약 Policy가 $\pi$로 주어지고 이 Policy를 따랐을 때 어떤 Epiosde에서 State $s$를 방문했다고 가정해봅시다. 그런데 한 Episode에서 State $s$를 꼭 한 번만 방문한다는 보장은 없습니다. 한 Episode에서 State $s$를 여러 번 방문했을 때 $v_{\pi}(s)$를 어떻게 구해야 할까요?

Monte Carlo 방법에는 First-visit MC Method와 Every-visit MC Method가 있습니다. 두 방법 모두 State $s$를 방문한 후, 얻은 Reward의 평균을 추정하는 것은 같습니다. 하지만 First-visit MC Method는 가장 처음에 방문한 것만 계산에 사용하고, Every-visit MC Method는 방문한 모든 것을 계산에 사용한다는 차이가 있습니다. 두 방법 모두 State $s$를 무한히 방문했을 때 $v_{\pi}(s)$에 수렴한다는 것은 같습니다.

이번 장에서는 First-visit MC Method를 위주로 살펴볼 예정이며, Every-visit MC Method는 9장과 12장에서 다시 다룰 예정입니다.

First-visit MC Method의 Pseudocode는 다음과 같습니다. 이 알고리즘을 Every-visit MC Method로 수정하려면 Unless ~ 로 시작하는 조건문을 삭제하면 됩니다.

Example 5.1) Blackjack

Blackjack 게임은 카지노에서 자주 보이는 카드 게임 중 하나로써, 딜러와 플레이어가 승부하는 게임입니다. 플레이어가 가지고 있는 카드의 합이 딜러가 가지고 있는 카드의 합보다 높거나 플레이어 카드의 합이 21일 경우 무조건 승리하지만, 21을 초과할 경우에는 무조건 패배합니다. 이 때, 특수한 카드인 Jack (J), Queen (Q), King (K)은 10으로 취급합니다. Ace (A)는 플레이어의 선택에 따라 1로 취급할 수도 있고 11로 취급할 수도 있습니다.

게임은 플레이어와 딜러가 각각 무작위한 2장의 카드를 받고 시작합니다. 이 때 플레이어의 카드는 모두 오픈하지만, 딜러는 1개만 오픈하고 1개는 뒤집어 놓습니다.

플레이어가 선택할 수 있는 Action은 Hit과 Stand입니다. Hit을 선택하면 무작위 카드를 한 장 더 받을 수 있고, Stand를 선택하면 카드를 더 받지 않습니다. 만약 Hit을 선택했을 때, 새로 받은 카드를 포함하여 합이 21을 초과할 경우 플레이어는 즉시 패배합니다. 이것을 Bust라고 합니다.

플레이어가 Stand를 선택하고 카드의 합이 21을 넘지 않는다면, 딜러가 게임을 시작합니다. 이 때 딜러는 자신의 의지대로 플레이할 수 없고, 카드의 합이 17보다 작으면 무조건 Hit을 해야하고, 그렇지 않으면 무조건 Stand를 해야합니다. 딜러가 Bust가 된다면 플레이어의 승리입니다.

만약 플레이어와 딜러 두 명 모두 Bust가 아니라면, 그 때 카드의 합을 비교하여 높은 쪽이 승리합니다.

Solution)

먼저 Blackjack 게임의 State와 Action, 그리고 Reward를 정의해봅시다.

• State

초기에 플레이어가 받은 카드 2장의 합 : 최소 12 - 최대 21 딜러가 가지고 있는 카드 중 공개된 1장의 숫자 : 최소 1 (Ace) - 최대 10 내가 Ace를 가지고 있는지에 대한 여부 : 예 or 아니오

따라서 State의 총 갯수는 10 * 10 * 2 = 200개입니다.

State는 (플레이어 카드의 합, 딜러의 카드, Ace 보유 여부) 로 표기합니다.

• Action

플레이어의 Action만 고려하면 되므로 Hit 또는 Stand로 2개입니다.

• Reward

플레이어가 게임에서 승리하면 +1, 패배하면, -1, 무승부일시 0으로 정의합니다.

다음으로 Policy를 세팅해보겠습니다. 교재에서는 현재 플레이어가 가지고 있는 카드의 합이 20, 21이면 Stand를 하고, 그 이외는 Hit을 선택하도록 Policy를 정의하였습니다. 이것을 가지고 Python을 사용하여 구현하면 다음과 같습니다.

import gym
import pandas as pd
from collections import defaultdict

env = gym.make('Blackjack-v1')
num_timesteps = 100

def policy(state):
    return 0 if state[0] > 19 else 1

def generate_episode(policy):
    episode = []
    state = env.reset()
    for t in range(num_timesteps):
        action = policy(state)
        next_state, reward, done, info = env.step(action)
        episode.append((state, action, reward))
        if done:
            break
        state = next_state

    return episode

total_return = defaultdict(float)
N = defaultdict(int)

num_iterations = 500000
for i in range(num_iterations):
    episode = generate_episode(policy)
    states, actions, rewards = zip(*episode)
    for t, state in enumerate(states):
        if state not in states[0:t]:
            R = (sum(rewards[t:]))
            total_return[state] = total_return[state] + R
            N[state] = N[state] + 1

total_return = pd.DataFrame(total_return.items(), columns=['state', 'total_return'])
N = pd.DataFrame(N.items(), columns=['state', 'N'])
df = pd.merge(total_return, N, on='state')
df['value'] = df['total_return'] / df['N']
print(df.head(10))

위의 코드는 First-visit MC Method로 Blackjack 게임에서 각 State의 Value를 추정한 프로그램입니다. (프로그램을 실행하기 위해서는 gym과 pandas 라이브러리를 설치하셔야 합니다) 만약 이 프로그램을 Every-visit MC Method로 바꾸고 싶다면, 32번째 Line의 if 문을 삭제하시면 됩니다.

프로그램을 실행하게 되면 많이 방문한 State 순으로 10개를 보여주고, 얻은 총 Return과 방문 횟수, 그리고 추정한 State의 Value를 출력합니다. 이 프로그램은 단순히 State의 Value만 추정하는 것이기 때문에 Policy를 변경하지는 않습니다. 이러한 방법으로 1만개와 50만개의 Episode를 경험한 후, State의 Value를 도식화하면 아래와 같습니다.

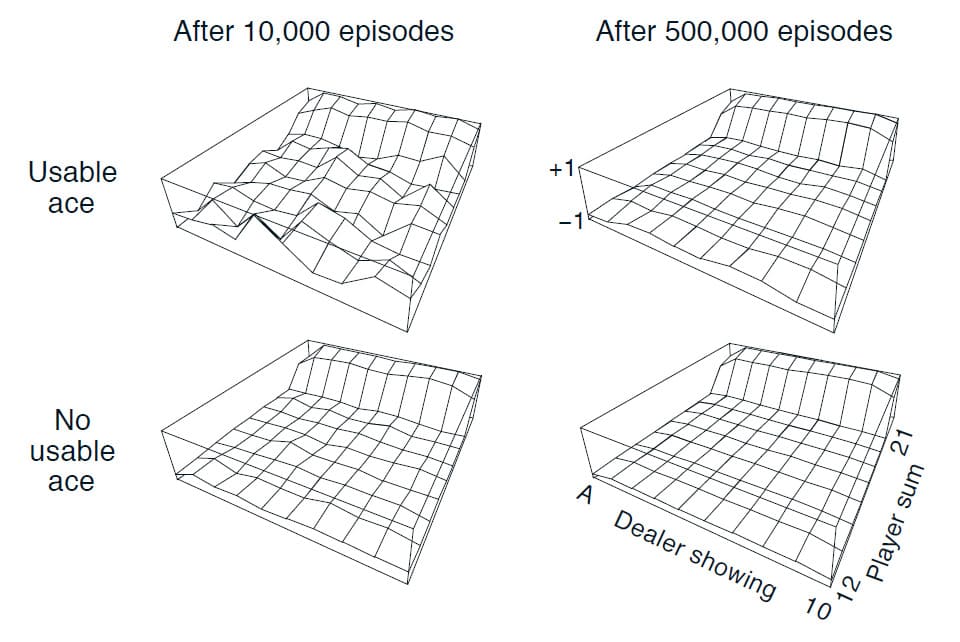
결과를 보면 State의 Value가 높은 경우는 카드의 합이 20과 21일 경우밖에 없습니다. 어떻게 보면 당연한게, 저희가 설정한 Policy는 20과 21에서만 Stand를 하기 때문입니다. Blackjack 게임에 대해서 잘 아는 것은 아니지만 18이나 19에서 Hit을 한다면 Bust할 확률이 높기 때문에 승률이 낮을 수밖에 없습니다.

□

예제로 보여드린 Blackjack 게임은 Environment에 대해 완전한 정보를 가지고 있습니다. 하지만 지난 장에서 배운 DP 방법으로 Blackjack 게임의 Value Function을 계산하는 것은 쉽지 않습니다. 가장 어려운 점은 Transition Probability를 계산하는 것입니다. 예를 들어, 현재 플레이어가 가지고 있는 카드의 합이 14이고 플레이어가 Stand를 선택했다고 가정했을 때, 플레이어가 이길 확률을 계산하면 얼마일까요? 이것부터가 쉽지 않은데 모든 State에 대해 이것을 계산해야 한다고 생각하면 막막할 따름입니다. 그렇기 때문에 Environment에 대한 지식을 알고있는지 여부에 상관없이 Monte Carlo Method는 DP보다 간단할 수 있습니다.

Monte Carlo Method에서 중요한 점은 각 State에 대해 추정한 Value가 독립적이라는 것입니다. 이것은 어떤 State에 대해 추정한 Value가 다른 State에 대해 추정한 Value에 영향을 끼치지 않는다는 뜻이므로, Bootstrap하지 않는다고 해석할 수 있습니다.

또한 Monte Carlo Method는 Episode에 기반하기 때문에, 특정(단일) State의 Value를 추정할 때의 계산 비용은 State의 수가 매우 많더라도 간단하게 계산할 수도 있습니다. 지난 장에서 DP를 사용할 때는 State의 Value를 추정하기 위해서 모든 State를 고려한 것을 생각해보면 확실히 낫다고 볼 수 있습니다.

Monte Carlo Estimation of Action Values

Model을 사용할 수 없는 경우, 즉 Environment에 대한 완전한 정보가 없는 경우에는 State-Value를 사용하는 것 보다 Action-Value를 사용하는 것이 더 좋습니다. Value를 기반으로 Policy를 만들 때는 각 Action에 대한 Value를 명시적으로 추정해야하기 때문입니다. 따라서 Monte Carlo Method의 주요 목표 중 하나는 $q_{*}$를 추정하는 것입니다. 그 목표를 이루기 위해서는 먼저 Action-Value에 대한 Policy Evaluation을 고려해야 합니다.

Action-Value에 대한 Policy Evaluation은 State $s$에서 시작하여 Action $a$를 선택한 후, Policy $\pi$를 따를 때의 기대 Reward인 $q_{\pi} (s, a)$를 추정하는 것입니다. 추정 방법은 State-Value를 추정하는 방법과 거의 유사합니다.

Action-Value에 대한 Policy Evaluation을 할 때 유일한 문제는 많은 State-Action 쌍이 방문되지 않을 수 있다는 것입니다. 특히 $\pi$가 Deterministic Policy인 경우, 각 State에 대해서는 하나의 Action만 선택하기 때문에 Policy가 선택하는 Action 외에는 모두 방문하지 않기 때문입니다. 2장에서 언급했듯이 Policy에 대한 평가가 제대로 작동하기 위해서는 지속적인 탐색이 보장되어야 합니다.

이 문제를 해결하기 위해서는 모든 State-Action 쌍이 선택될 확률을 0보다 크게 만드는 것입니다. 아무리 작은 확률이라도 무한한 샘플을 얻게 되면 모든 State-Action 쌍을 많이 방문하게 되므로 제대로 Policy Evaluation을 할 수 있습니다. 이것을 Assumption of Exploring Starts라고 부릅니다.

Assumption of Exploring Starts는 때때로 유용하지만, Environment와 실제 상호 작용을 하며 직접 학습할 때는 일반적으로 신뢰할 수 없습니다. 모든 State-Action 쌍을 방문할 수 있게 만들기 위해서는 차라리 Stochastic Policy를 고려하는 것이 낫습니다. 이번 장 뒷부분에서는 그렇게 접근하는 2가지 방법에 대해 설명하겠지만, 일단 지금은 Assumption of Exploring Starts를 유지하면서 Monte Carlo Control 방법을 소개하도록 하겠습니다.

Monte Carlo Control

Monte Carlo Prediction의 기본 아이디어는 지난 장에서 배웠던 Generalized Policy Iteration (GPI)과 동일합니다. 교재에서는 Monte Carlo Method가 DP와 달리 Environment에 대한 지식 없이 샘플 Episode 만으로 Optimal Policy와 Value Function을 찾는 데 사용할 수 있다는 것을 보여주지만, 굳이 이 부분까지 설명할 필요는 없을 것 같아서 생략하도록 하겠습니다.

Monte Carlo Method로 수렴한다는 보장을 얻기 위해서 저희는 2가지 가정을 했습니다. 하나는 Assumption of Exploring Starts이고, 다른 하나는 무한한 수의 Episode가 있다는 가정입니다. 하지만 두 가정 모두 현실적이지 않기 때문에 Monte Carlo 알고리즘을 만들기 위해서는 이 두 가정을 모두 제거할 필요가 있습니다. 첫 번째 가정은 나중에 고려하도록 하고, 우선 무한한 수의 Episode에 대해서만 생각해보도록 하겠습니다.

첫 번째로 생각할 수 있는 해결 방법은 각각의 Policy Evaluation이 $q_{\pi_k}$를 근사화한다는 아이디어를 유지하는 것입니다. 즉, 어느 정도 근사치까지 정확한 수렴을 보장한다는 의미이지만, 문제의 크기가 조금만 커져도 실제와 가깝게 근사화하기 위해서는 너무 많은 Episode가 필요하다는 문제가 있습니다.

두 번째로 생각할 수 있는 해결 방법은 Policy Improvement를 하기 전에 Policy Evaluation을 끝내지 않는 것입니다. Policy Evaluation은 매 단계마다 Value Function을 $q_{\pi_k}$에 가까워지게 하는 시도를 하지만, 어차피 후반 몇몇 단계를 제외하고는 실제로 그렇게 가깝지 않습니다. 지난 장에서 GPI를 처음 소개할 때 잠깐 소개했었는데, 극단적으로는 Policy Evaluation을 한 번만 수행하는 것도 가능하다고 했었습니다.

Monte Carlo Method에서의 Policy Iteration은 각 Episode별로 Evaluation과 Improvement를 번갈아 수행합니다. 각 Episode에서 발생한 Reward는 Policy Evaluation에 사용되며, Episode에서 방문한 모든 State에서 Policy가 Improve 됩니다. 이것을 Monte Carlo with Exploring Starts라고 하며 Pseudocode는 다음과 같습니다.

Monte Carlo with Exploring Starts는 초기 Policy에 상관없이 모든 State-Action 쌍에 대한 평균적인 Reward를 얻을 수 있습니다. 이전에 Monte Carlo Prediction에서는 Policy에 대한 평가만 했다면, Monte Carlo with Exploring Starts는 Policy를 업데이트하는 기능이 추가되며, Optimal Policy로 수렴할 것이라고 생각됩니다. 생각됩니다 라고 쓰는 이유는 아직 공식적으로 증명되지 않았기 때문입니다.

Example 5.3) Solving Blackjack

Example 5.1에서 다루었던 Blackjack 게임을 다시 언급해보겠습니다. Example 5.1에서는 Policy에 대한 Value만을 계산했지만, Monte Carlo with Exploring Starts을 적용하게 되면 Optimal Policy를 구할 수 있습니다. 이를 도식화하면 아래 그림과 같습니다.

□

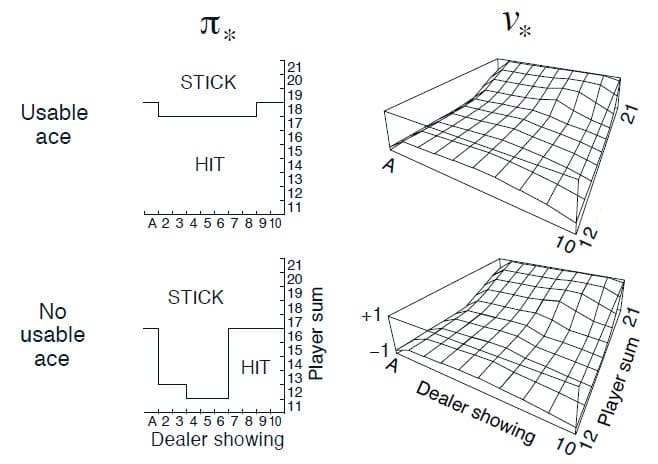
Monte Carlo Control without Exploring Starts

이번에는 Assumption of Exploring Starts를 제거해보도록 하겠습니다. Assumption of Exploring Starts 없이 모든 Action이 선택될 수 있게 하는 유일한 방법은 Agent로 하여금 모든 State를 골고루 선택하게 설계하는 것입니다. 이를 보장하는 방법이 2가지 있는데, 하나는 On-policy 방법이고 다른 하나는 Off-policy 방법입니다. On-policy 방법은 Agent가 실제로 사용한 Policy를 Evaluation하거나 Improvement하는 방법이고, Off-policy 방법은 실제로 사용한 Policy와 다른 Policy를 Evaluation하거나 Improvement하는 방법입니다. 직전에 다룬 Monte Carlo with Exploring Starts는 On-policy 방법의 한 종류라고 볼 수 있습니다. 먼저 On-policy에 대해 알아본 다음, Off-policy 방법은 다음 섹션에서 다루도록 하겠습니다.

On-policy 방법은 모든 State $s \in \mathcal{S}$와 모든 Action $a \in \mathcal{A} (s)$에 대해 $\pi (a \mid s) > 0$으로 시작하지만, 점차적으로 (Optimal) Deterministic Policy에 가까워집니다. 이것을 유도하는 방법은 여러 개가 있지만, 우선 가장 많이 쓰이는 $\epsilon$-Greedy Policy를 먼저 소개하도록 하겠습니다. $\epsilon$-Greedy Policy는 일반적으로 Value가 가장 높은 Action을 선택하지만, 낮은 확률로 무작위 Action을 선택하는 방법입니다. 조금 더 구체적으로 설명하자면 $\epsilon > 0$의 확률로 무작위 Action을 선택하고 $1 - \epsilon$의 확률로 Value가 가장 높은 Action을 선택하는 것입니다.

$\epsilon$-Greedy Policy에서 $\epsilon$의 값은 고정된 값이 아닙니다. Value가 제대로 추정되지 않은 초기에는 $\epsilon$을 크게 만들어서 여러 Action을 선택하게 유도하고, 어느 정도 추정이 끝난 다음에는 $\epsilon$를 작게 만들어 최선의 선택을 하도록 유도하는 것입니다.

On-policy Monte Carlo Control에서도  현재 Policy에 대한 Action-Value Function을 추정하기 위해 First-visit MC Method를 사용합니다. Monte Carlo with Exploring Starts와 달리 Assumption of Exploring Starts를 하지 않고, 대신 $\epsilon$-Greedy Policy를 사용합니다. $\epsilon$-Greedy와 같은 Policy를 $\epsilon$-soft라고도 부릅니다. On-policy Monte Carlo Control의 Pseudocode는 다음과 같습니다.

$\epsilon$-Greedy Policy로부터 $q_{\pi}$를 개선하는 것은 Policy Improvement Theorem에 의해 보장됩니다. 이에 대한 유도는 다음과 같습니다.

\[\begin{align} q_{\pi} (s, \pi' (s)) &= \sum_a \pi' (a | s) q_{\pi} (s, a) = \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a q_{\pi} (s, a) + (1 - \epsilon) \max_a q_{\pi} (s, a) \tag{5.2} \\ \\ &\ge \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a q_{\pi} (s, a) + (1 - \epsilon) \sum_a \frac{\pi (a | s) - \frac{\epsilon}{|\mathcal{A}(s)|}}{1-\epsilon} \\ \\ &= \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a q_{\pi} (s, a) - \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a q_{\pi} (s, a) + \sum_a \pi (a | s) q_{\pi} (s, a) = v_{\pi} (s) \end{align}\]

위의 전개식은 Policy Improvement Theorem에 의해 $\pi^{\prime} \ge \pi$임을 보여주고 있습니다. 두 번째로 증명해야할 부분은 두 Policy $\pi^{\prime}$와 $\pi$가 최적의  $\epsilon$-soft Policy일 때, 다른 $\epsilon$-soft Policy보다 좋거나 같아야 한다는 것입니다.

이것을 증명하기 위해 먼저 Policy가 $\epsilon$-soft 로 이동되어야 한다는 조건을 제외하고 원래 Environment과 동일한 새 Environment를 가정해보겠습니다. 새 Environment에서는 원래 Environment와 동일한 State와 Action 집합이 설정되어 있습니다. 새 Environment에서는 State $s$에서 Action $a$를 선택했을 때 $1 - \epsilon$ 확률로 원래 Environment와 동일하게 동작하며, $\epsilon$ 확률로 무작위 Action을 선택한 다음 새로운 Action으로 이전 Environment처럼 동작합니다. 이런 새로운 Environment에서 할 수 있는 최선의 Policy는 원래 Environment에서 할 수 있는 최선의 Policy와 동일합니다. $\tilde{v}_{*}$와 $\tilde{q}_{*}$를 새 Environment에서 Optimal Value Function라고 정의하면, Policy $\pi$는 $v_{\pi} = \tilde{v}_{*}$인 경우에만 $\epsilon$-soft Policy 중 최선의 Policy입니다. 먼저 Transition Probability가 변경되었을 때 $\tilde{v}_{*}$는 Bellman Optimality Equation (식 3.19)에 대한 고유한 해법임을 다음을 통해 알 수 있습니다.

\[\begin{align} \tilde{v}_* &= \max_a \sum_{s', r} \left[ (1 - \epsilon) p (s', r | s, a) + \sum_{a'} \frac{\epsilon}{|\mathcal{A}(s)|} p (s', r | s, a') \right] \left[ r + \gamma \tilde{v}_* (s') \right] \\ \\ &= (1 - \epsilon) \max_a \sum_{s', r} p(s', r | s, a) \left[ r + \gamma \tilde{v}_*(s') \right] + \frac{\epsilon}{|\mathcal{A(s)}|} \sum_a \sum_{s', r} p (s', r |s, a) \left[ r + \gamma \tilde{v}_*(s') \right] \end{align}\]

다음으로 $\epsilon$-soft Policy $\pi$가 더 이상 개선되지 않고, $v_{\pi} = \tilde{v}_*$가 성립하면 식 (5.2)에 의하여 다음이 성립합니다.

\[\begin{align} v_{\pi} (s) &= (1 - \epsilon) \max_a q_{\pi} (s, a) + \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a q_{\pi} (s, a) \\ \\ &= (1 - \epsilon) \max_a \sum_{s', r} p (s', r | s, a) \left[ r + \gamma v_{\pi} (s') \right] + \frac{\epsilon}{|\mathcal{A}(s)|} \sum_a \sum_{s', r} p (s', r |s, a) \left[ r + \gamma v_{\pi} (s') \right] \end{align}\]

그러나 이 방정식은 $\tilde{v}_{*}$를 $v_{\pi}$로 대입한 것을 제외하고는 앞의 방정식과 동일합니다. 여기서 $\tilde{v}_{*}$는 유일한 해법이므로 $v_{\pi} = \tilde{v}_{*}$일 수밖에 없습니다.

결과적으로 $\epsilon$-soft Policy에서 Policy Iteration은 정상적으로 작동한다는 것을 알 수 있습니다. 또한 이제는 Assumption of Exploring Starts 없이 $\epsilon$-soft Policy에 대한 Improvement만으로 Optimal Policy를 찾을 수 있다는 것을 보장할 수 있습니다.

Off-policy Prediction via Importance Sampling

이전 섹션에서 배운 On-policy 방법의 가장 큰 단점은 Policy를 평가하기 위해서 실제로 경험해봐야 한다는 것입니다. 이 말은 최적의 Action을 찾기 위해 그렇지 않은 Action을 반드시 해봐야한다는 의미입니다. 이것을 해결하는 방법은 Target Policy와 Behavior Policy를 분리하는 것입니다. 이렇게 두 Policy를 분리하여 학습하는 방법을 Off-policy 방법이라고 합니다. 이렇게 이름을 붙이는 이유는 Target Policy에 Off 된다는 의미이기 때문이라고 합니다.

Off-policy 방법은 On-policy 방법에 비해 일반적으로 많이 사용합니다. 특히 인간 전문가로부터 생성되는 데이터나, 비학습적인 컨트롤러로부터 생성되는 데이터를 학습하는데 우수한 성능을 가지고 있습니다. 그러나 Off-policy 방법은 On-policy 방법에 비해 추가적인 개념이 필요하기 때문에 더 복잡하고, 학습 데이터가 다르게 주어지기 때문에 분산이 더 크며, 수렴 속도 또한 더 느리다는 단점이 있습니다. 그렇기 때문에 On-policy 방법과 Off-policy 방법은 서로 우열을 가리기 어려우며, 두 방법 모두 상황에 따라 잘 사용되고 있습니다.

이번 섹션에서 다룰 Off-policy 방법에서 Target Policy는 $\pi$, Behavior Policy는 $b$로 표기하며, 두 Policy 모두 고정되어 주어진 것으로 가정하겠습니다.

Policy $b$로부터 생성된 Episode를 사용하여 Policy $\pi$를 추정하기 위해서는 $\pi$에서 수행한 모든 Action이 적어도 가끔은 $b$에서도 수행되어야 합니다. 즉, 여기에는 $\pi (a \mid s) > 0$일 경우 반드시 $b(a \mid s) > 0$라는 것을 의미합니다. (이것을 Assumption of Coverage라고 합니다) 또한 Policy $\pi$는 Deterministic일 수 있으나, Policy $b$는 Stochastic이어야 합니다.

Off-policy 방법에서 또 한가지 중요한 것은 바로 Importance Sampling입니다. 처음 강화학습을 공부했을 때 Importance Sampling에 대한 개념이 난해해서 이해하기 힘들었는데, 좋은 포스팅을 발견하여 여기에 잠깐 소개하도록 하겠습니다. (원본 포스트 링크)

Example of Importance Sampling)

어느 섬에 키다리족과 난장이족이 있습니다. 문제를 쉽게 하기 위해 이 섬의 사람은 키가 160cm 아니면 180cm 둘 중 하나라고 가정하도록 하겠습니다. 오랜 시간에 걸쳐 키다리족과 난장이족의 인구 분포를 조사한 결과, 다음과 같은 키의 분포가 나왔습니다. 이 때, 확률 변수 X를 키다리족, 확률 변수 Y를 난장이족이라고 정의하도록 하겠습니다.

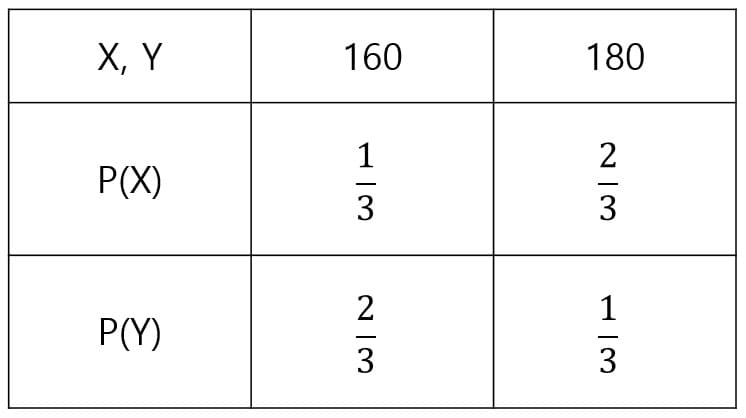
그리고 이번에는 두 부족의 평균 키를 구하려고 합니다. 먼저 키다리족의 사람 중 무작위로 10명의 표본을 뽑았더니, 다음과 같은 키의 분포가 나왔습니다.

160 160 160 160 180 180 180 180 180 180

이 분포를 토대로 표본집단의 평균을 구하는 것은 간단합니다. 표본집단의 평균은 모집단의 평균과 유사하니 완벽하게 일치하지는 않겠지만 모집단의 평균을 대략적으로 유추할 수 있습니다.

이번에는 난장이족의 평균 키를 구하려고 합니다. 난장이족도 마찬가지로 무작위 표본을 뽑아 평균을 구하면 간단하지만, 모종의 문제로 난장이족의 표본을 구할 수 없다고 가정해봅시다. 대신 우리는 키다리족의 표본을 구했었고, 난장이족과 키다리족의 키의 분포를 알고 있습니다.

이 키다리족의 표본을 토대로 난장이족의 키의 표본을 생성해봅시다. 먼저, 키가 160cm인 사람의 비율은 난장이족이 키다리족보다 2배가 많습니다. 그렇기 때문에 키가 160cm인 사람의 비율을 2배로 늘립니다.

160 160 160 160 160 160 160 160 180 180 180 180 180 180

다음으로 키가 180cm인 사람의 비율을 보면 키다리족이 난장이족보다 2배가 많습니다. 그래서 키가 180cm인 사람의 비율을 절반으로 줄입니다.

160 160 160 160 160 160 160 160 180 180 180

이렇게 구한 표본을 토대로 평균을 구한다면, 이것은 난장이족의 평균 키라고 말할 수 있습니다. 이것이 바로 Importance Sampling의 한 예입니다.

□

이번에는 강화학습에서의 Importance Sampling이 무엇인지 알아보겠습니다. 위의 예제에서 키다리족의 표본으로 난장이족의 데이터를 추정했듯이, Off-policy에서도 Behavior Policy $b$로부터 생성되는 데이터를 토대로 Target Policy $\pi$를 추정해야 합니다. 예제에서는 키다리족과 난장이족의 키의 분포가 미리 주어졌으나, 여기에서는 문제마다 다르기 때문에 직접 계산해야합니다. 이렇게 두 데이터 사이의 비율을 Importance Sampling Ratio라고 합니다. 이것을 수식으로 표현하기 위해, 먼저 State $S_t$에서 시작하여 State-Action Trajactory를 얻을 확률을 구하도록 하겠습니다.

\[\begin{align} &Pr \left\{ A_t, S_{t+1}, A_{t+1}, ... , S_T | S_t, A_{t:T-1} ~ \pi \right\} \\ \\ &= \pi (A_t | S_t ) p (S_{t+1} | S_t, A_t) \pi (A_{t+1} | S_{t+1}) \cdots p (S_T | S_{T-1}, A_{T-1}) \\ \\ &= \prod_{k=t}^{T-1} \pi (A_k | S_k) p ( S_{k+1} | S_k, A_k) \end{align}\]

위 식에서 $p$는 식 (3.4)에서 정의한 State Transition Probability입니다. 위 식을 토대로 Target Policy와 Behavior Policy 간의 Importance Sampling Ratio를 구하면 다음과 같습니다.

\[\rho_{t:T-1} \doteq \frac{\prod_{k=t}^{T-1} \pi (A_k | S_k) p ( S_{k+1} | S_k, A_k)}{\prod_{k=t}^{T-1} b (A_k | S_k) p ( S_{k+1} | S_k, A_k)} = \prod_{k=t}^{T-1} \frac{\pi (A_k | S_k)}{b (A_k | S_k)} \tag{5.3}\]

$p$는 MDP에서 주어지지 않는 한 구하기 가장 어려운 데이터지만, 운이 좋게도 분자와 분모 모두 있기 때문에 약분이 가능합니다. 즉, 두 Policy $\pi$와 $b$의 Importance Sampling Ratio는 두 Policy가 각 State에서 특정 Action을 선택할 확률이 얼마인지만 알면 구할 수 있습니다. 즉, Importance Sampling Ratio는 MDP에 독립적입니다.

Target Policy에서의 기대 Reward를 추정할 때 주의할 점은, Behavior Policy로 인한 Return인 $G_t$만 주어졌다는 것입니다. 이것으로는 $\mathbb{E} \left[ G_t \mid S_t = s \right] = v_b (s)$을 구할 수 있기 때문에 $v_{\pi}$를 얻을 수 없습니다. 그렇기 때문에 Importance Sampling이 필요한 것입니다. Importance Sampling Ratio $\rho_{t:T-1}$를 추가하면 원하는 $v_{\pi}$를 얻을 수 있습니다.

\[\mathbb{E} \left[ \rho_{t:T-1} G_t | S_t = s \right] = v_{\pi} (s) \tag{5.4}\]

이로써 Behavior Policy $b$로 생성된 Episode를 토대로 $v_{\pi} (s)$를 추정하는 Monte Carlo 알고리즘을 만들 준비가 되었습니다. 하나 추가할 점은 앞으로 각 Episode에서의 시간 단계는 이어지게 표현하겠습니다. 예를 들어, 첫 번째 Episode가 $t = 100$에서 종료되었다면, 다음 Episode는 $t = 101$에서 시작하는 방식입니다. 이를 통해 특정 Episode의 특정 단계를 참조하기 위해 시간 단계를 사용할 수 있고, $\mathcal{T}(s)$라는 표기로 State $s$를 방문하는 모든 시간 단계 집합을 정의할 수 있습니다. 이 표기가 유용한 이유는 Every-visit MC 알고리즘을 사용할 때 표현이 간단해지기 때문입니다. 또한 $T(s)$라는 표기를 통해 시간 단계 $t$ 이후 처음으로 Episode가 종료되는 시점을 나타나게 하겠습니다. 이렇게 되면 $G_t$가 시간 단계 $t$ 이후에서 $T(s)$까지의 Return을 의미하게 됩니다. 또한 $\{ G_t \}_{t \in \mathcal{T}(s)}$는 State $s$에 대한 Return을 의미하고, $\{ \rho_{t:T(t)-1} \}_{t \in \mathcal{T}(s)}$는 Importance Sampling Ratio를 의미합니다. 여러 표기가 갑자기 나와서 헷갈리실 수 있는데, 어쨌든 중요한 것은 이게 다 $v_{\pi} (s)$를 간단하게 표현하기 위함입니다. 방금 새로 정의한 표기를 사용하여 $V(s)$를 표현하면 다음과 같습니다.

\[V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \rho_{t:T(t)-1} G_t}{|\mathcal{T}(s)|} \tag{5.5}\]

식 (5.5)와 같이 Importance Sampling을 단순한 평균으로 계산하는 것을 Ordinary Importance Sampling이라고 합니다. 단순한 평균 대신 Weighted Average를 사용할 수도 있는데, 이 때는 Weighted Importance Sampling이라고 하며, $V(s)$는 다음과 같이 정의됩니다.

\[V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \rho_{t:T(t)-1} G_t}{\sum_{t \in \mathcal{T}(s)} \rho_{t:T(t)-1}} \tag{5.6}\]

식 (5.6)에서 만약 분모가 0인 경우에는 $V(s)$를 그냥 0으로 정의합니다.

이 두 가지 Importance Sampling를 비교하기 위해 State $s$에서 단 하나의 Return을 관찰한 후 First-visit MC Method를 사용한다고 가정해보겠습니다. Weighted Importance Sampling에서는 ($\Sigma$ 기호가 없어지기 때문에) $\rho_{t:T(t)-1}$가 약분되므로 $V(s)$가 Return $G_t$와 동일해집니다. 단 하나의 Return만 관찰되었기 때문에 이것이 합리적으로 보일 수 있지만, 이것은 $v_b (s)$의 기대값이기 때문에 통계적으로 Bias되었다고 볼 수 있습니다. 반대로 Ordinary Importance Sampling에서는 단 하나의 Return이더라도 $v_{\pi} (s)$의 기대값이기 때문에 Bias되지는 않지만, 값 자체는 극단적일 수 있습니다. 예를 들어 Importance Sampling Ratio가 10이라면 관찰된 Trajactory가 Behavior Policy보다 Target Policy에서 10배 더 가치가 있다고 판단되고, 해당 Episode Trajactory가 Policy를 훌륭하게 대표한다고 가정해도 실제로 관측되는 Reward와는 크게 차이나는 문제가 있습니다.

따라서 First-visit MC Method에서 두 가지 Importance Sampling에 대한 차이는 Bias와 Variance의 차이라고 볼 수 있습니다. Ordinary Importance Sampling은 Bias되지 않지만 Variance이 무한하게 커질 수 있으며, Weighted Importance Sampling은 극단적인 경우에도 Variance가 1이지만(위의 예제) Bias라는 문제가 있습니다. 두 방법 모두 장단점이 있지만, 일반적으로는 Bounded Return 환경에서 Variance가 0으로 수렴하는 Weighted Importance Sampling을 더 선호하는 편입니다.

Every-visit MC Method에서는 Ordinary Importance Sampling과 Weighted Importance Sampling 모두 Bias되지만 Sample의 수가 증가할수록 Bias가 0에 가까워집니다. 그렇기 때문에 Off-policy에서는 Every-visit MC Method가 선호됩니다. Weighted Importance Sampling을 사용한 Off-policy Every-visit MC 알고리즘은 다음과 같습니다.

Incremental Implementation

이번 Section의 이름은 2.4와 동일합니다. 그 때와 마찬가지로 On-policy Monte Carlo Method를 Recurrence Relation으로 표현하는 방법에 대해 알아보겠습니다. Off-policy Monte Carlo Method는 Importance Sampling을 어떻게 구현하는지에 따라 달라집니다. Ordinary Importance Sampling에서의 Return은 식 (5.3)처럼 $\rho_{t:T(t)-1}$의 비율로 조정되고 식 (5.5)처럼 평균화됩니다. 이렇게하면 Section 2.4에서 사용했던 방법을 그대로 사용할 수 있지만, Weighted Importance Sampling일 때 사용하기 위해서는 약간 다른 알고리즘이 필요합니다.

Return의 Sequence $G_1, G_2, \ldots, G_{n-1}$이 있다고 가정해봅시다. 이 Return들은 모두 동일한 State에서 시작하고 각각 해당하는 무작위 Weight $W_i$를 가집니다. 그렇다면 이것의 Value Function을 다음과 같이 추정할 수 있습니다.

\[V_n \doteq \frac{\sum_{k=1}^{n-1} W_k G_k}{\sum_{k=1}^{n-1} W_k}, \quad n \ge 2 \tag{5.7}\]

식 (5.7)을 그대로 사용하면 Return $G_n$을 얻을 때마다 $V_n$을 다시 계산해야하는 불편함이 있습니다. Weighted Expectation을 구하기 위해선 Section 2.4에서 다루었던 Recurrence Relation을 약간 변경하여, Cumulative Sum $C_n$를 추가합니다. 먼저 $V_n$의 Recurrence Relation은 다음과 같습니다.

\[V_{n+1} \doteq V_n + \frac{W_n}{C_n} \left[ G_n - V_n \right] , \quad n \ge 1, \tag{5.8}\]

그리고 $C_n$의 Recurrence Relation은 다음과 같습니다.

\[C_{n+1} \doteq C_n + W_{n+1}\]

이 때, $C_0 \doteq 0$으로 정의합니다. 이것을 반영한 Off-policy Monte Carlo Prediction 알고리즘은 다음과 같습니다. 아래 알고리즘은 Weighted Importance Sampling으로 구현되었습니다. 만약 On-policy로 바꾸고 싶다면, Target Policy와 Behavior Policy가 같다는 뜻이므로 ($\pi = b$), $W = 1$로 설정하면 됩니다.

Off-policy Monte Carlo Control

이제 Off-policy Monte Carlo Prediction을 완성했으니, Control 방법을 제시할 준비가 되었습니다. On-policy에서는 Control를 위해 Policy의 Value를 추정하면서 Policy를 사용했으나, Off-policy는 두 기능이 분리된다는 차이점이 있습니다. 그렇기 때문에 Behavior Policy는 Action을 선택하는데만 사용하고, Target Policy는 Policy를 Evaluation 및 Improvement하는데 이 둘이 전혀 연관이 없을 수 있습니다. 이렇게 구분하게 되면 각 Action의 Value에 상관 없이 모든 Action을 계속 Sampling할 수 있다는 장점이 있습니다.

Off-policy Monte Carlo Control 방법은 앞에 두 Section에서 제안한 기법 중 하나를 사용합니다. 이 때, Behavior Policy는 모든 State의 모든 Action에 대해서 선택할 확률이 0보다 커야합니다. (=Soft)

위의 의사 코드는 $\pi_{*}$와 $q_{*}$를 추정하기 위해 GPI와 Weighted Importance Sampling을 기반으로 하는 Off-policy Monte Carlo Control 알고리즘입니다. Target Policy $\pi \approx \pi_{*}$는 $q_{\pi}$의 추정치인 Q에 대해 Greedy한 Policy이고, Behavior Policy $b$는 $\epsilon$-soft로 선택함으로써 $\pi$의 수렴을 Optimal Policy로 보장하였습니다. 따라서 Policy $\pi$는 Policy $b$에 따라 Action을 선택하더라도 최적으로 수렴하는 것이 보장됩니다.

이 Control 방법의 문제는 Episode의 나머지 Action이 Greedy일 때 Episode의 마지막 부분에서만 학습이 된다는 것입니다. 만약 대부분의 Action이 greedy가 아니라면 학습 속도는 그만큼 느릴 수밖에 없습니다. 특히 Episode의 길이가 길수록 이 문제는 더욱 심각해집니다. 이것을 해결하기 위한 방법은 다음 장에서 주요하게 다룰 예정입니다. 지금은 $\gamma$가 1보다 작은 특수한 경우, 이것을 해결할 수 있는 간단한 방법을 다음 두 Section에 걸쳐 알아보겠습니다.

Discounting-aware Importance Sampling

지금까지 논의했던 Off-policy 방법은 Discount와 같은 Return의 구조를 고려하기 보단, Importance Sampling Ratio를 계산하는 것에 중점을 두었습니다. 이제는 이것을 토대로 Off-policy Prediction에서의 Variance를 줄이기 위한 아이디어를 논의해 보겠습니다.

예를 들어, Episode의 길이가 100단계이고 $\gamma = 0$인 상황이라고 가정하겠습니다. 그렇다면 $t=0$에서의 Return은 $G_0 = R_1$이지만, Importance Sampling Ratio는 $\frac{\pi (A_0 \mid S_0)}{b (A_0 \mid S_0)} \frac{\pi (A_1 \mid S_1)}{b (A_1 \mid S_1)} \cdots \frac{\pi (A_99 \mid S_99)}{b (A_99 \mid S_99)}$ 와 같이 100 항의 곱셉으로 이루어져 있습니다. Ordinary Importance Sampling에서의 Return은 실제로 첫 번째 항인 $\frac{\pi (A_0 \mid S_0)}{b (A_0 \mid S_0)}$외에는 독립적이지만, 대신 Variance가 엄청나게 커질 수 있습니다. 지금부터 이 Variance를 피하기 위한 아이디어를 논의하겠습니다.

아이디어의 핵심은 Discounting을 Episode가 종료될 확률이나 부분적으로 종료될 확률로 생각하는 것입니다. 임의의 $\gamma \in \left[ 0, 1 \right)$에 대해, Episode는 $t=1$에서 $1 - \gamma$ 확률로 부분 종료될 수 있습니다. 이 때의 Return은 $R_1$이 됩니다. 마찬가지로 $t=2$에서 Episode가 부분 종료될 확률은 $(1 - \gamma) \gamma$이며, 이 때의 Return은 $R_1 + R_2$가 되는 방식입니다. 이런 방식으로 얻은 Return을 Flat Partial Return이라고 합니다. 임의의 시간 $t$부터 $h$까지의 Flat Partial Return은 다음과 같이 정의됩니다.

\[\bar{G}_{t:h} \doteq R_{t+1} + R_{t+2} + \cdots + R_{h}, \quad 0 \le t < h \le T\]

Flat Partial Return에서 Flat은 Discounting이 없다는 것을 의미하고, Partial은 Return이 Episode가 종료되기 전인 Horizon $h$에서 중지된다는 것을 의미합니다. 기존의 전체 Return $G_t$는 다음과 같이 Flat Partial Return의 합계로 표현할 수 있습니다.

\[\begin{align} G_t & \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots \gamma^{T-t-1} R_T \\ \\ &= (1 - \gamma) R_{t+1} + (1 - \gamma) \gamma (R_{t+1} + R_{t+2}) + (1 - \gamma) \gamma^2 (R_{t+1} + R_{t+2} + R_{t+3}) \\ \\ & \cdots + (1 - \gamma) \gamma^{T-t-2} (R_{t+1} + R_{t+2} + \cdots +  R_{T-1}) + \gamma^{T-t-1} (R_{t+1} + R_{t+2} + \cdots +  R_{T}) \\ \\ &= (1 - \gamma) \sum_{h=t+1}^{T-1} \gamma^{h-t-1} \bar{G}_{t:h} + \gamma^{T-t-1} \bar{G}_{t:T} \end{align}\]

Flat Partial Return을 제대로 사용하기 위해서는 Importance Sampling Ratio 또한 적절하게 조절해야 합니다. Return $\bar{G}_{t:h}$는 $h$까지의 Reward만 포함하기 때문에 $h-1$까지의 Ratio를 구하면 됩니다. 식 (5.5)와 유사하게, Ordinary Importance Sampling은 다음과 같이 정의할 수 있습니다.

\[V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \left( (1 - \gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t:h-1} \bar{G}_{t:h} + \gamma^{T(t)-t-1} \rho_{t:T(t)-1} \bar{G}_{t:T(t)} \right)}{|\mathcal{T}(s)|} \tag{5.9}\]

Weighted Importance Sampling의 경우에는 식 (5.6)과 유사하게 다음처럼 정의할 수 있습니다.

\[V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \left( (1 - \gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t:h-1} \bar{G}_{t:h} + \gamma^{T(t)-t-1} \rho_{t:T(t)-1} \bar{G}_{t:T(t)} \right)}{\sum_{t \in \mathcal{T}(s)} \left( (1 - \gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t:h-1} + \gamma^{T(t)-t-1} \rho_{t:T(t)-1} \right)} \tag{5.10}\]

이렇게 $V(s)$를 추정하는 것을 Discounting-aware Importance Sampling Estimator라고 부릅니다. 가장 큰 특징은 이 추정 방법은 Discount Factor를 고려하지만 $\gamma = 1$인 경우는 효과가 없다는 것입니다. (Section 5.5의 Off-policy 추정과 동일함)

Per-decision Importance Sampling

Off-policy Importance Sampling에서 Discounting이 없는 경우(즉, $\gamma = 1$)에도 Variance를 줄일 수 있는 또 다른 방법이 있습니다. Off-Policy를 나타낸 식 (5.5)와 (5.6)에서 분자에 있는 합계의 각 항은, 각각이 Reward에 대한 Return으로 표현될 수 있습니다.

\[\begin{align} \rho_{t:T-1} G_t &= \rho_{t:T-1} \left( R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-t-1} R_T \right) \\ \\ &= \rho_{t:T-1} R_{t+1} + \gamma \rho_{t:T-1} R_{t+2} + \cdots + \gamma^{T-t-1} \rho_{t:T-1} R_T \tag{5.11} \end{align}\]

위의 식 (5.11)을 보시면 각각의 항은 Return과 Importance Sampling Ratio의 곱으로 이루어져 있습니다. 즉, 이것은 Importance Sampling Ratio 비율을 가중치로 사용한 Weighted Average라고 볼 수도 있습니다. 이것을 더 간단한 방법으로 표현하기 위해서는, 식 (5.3)을 이용할 수 있습니다. 예를 들어, 식 (5.3)을 사용하면 첫 번째 항을 다음과 같이 표현할 수 있습니다.

\[\rho_{t:T-1} R_{t+1} = \frac{\pi (A_t | S_t)}{b (A_t | S_t)} \frac{\pi (A_{t+1} | S_{t+1})}{b (A_{t+1} | S_{t+1})} \frac{\pi (A_{t+2} | S_{t+2})}{b (A_{t+2} | S_{t+2})} \cdots \frac{\pi (A_{T-1} | S_{T-1})}{b (A_{T-1} | S_{T-1})} R_{t+1} \tag{5.12}\]

식 (5.12)는 매우 길지만, 사실 이렇게 많은 항의 곱셈 중에서 첫 번째 항과 마지막 항(=$R_{t+1}$)만 유효합니다. 왜냐하면 나머지는 어차피 모두 Return을 얻은 후에 발생한 이벤트이기 때문입니다. 나머지 항에 대한 기대값은 다음과 같이 정리할 수 있습니다.

\[\mathbb{E} \left[ \frac{\pi (A_k | S_k}{b (A_k | S_k} \right] \doteq \sum_a b (a|S_k) \frac{\pi (a|S_k)}{b (a|S_k)} = \sum_a \pi (a|S_k) = 1 \tag{5.13}\]

이런 식으로 몇 가지 단계를 더 거치면 왜 첫 번째 항과 마지막 항 이외에는 유효하지 않은지 알 수 있습니다.

\[\mathbb{E} \left[ \rho_{t:T-1} R_{t+1} \right] = \mathbb{E} \left[ \rho_{t:t} R_{t+1} \right] \tag{5.14}\]

식 (5.11)의 $k$번째 항에 대해 이 과정을 반복하면 다음을 얻습니다.

\[\mathbb{E} \left[ \rho_{t:T-1} R_{t+k} \right] = \mathbb{E} \left[ \rho_{t:t+k-1} R_{t+k} \right]\]

따라서 식 (5.11)의 기대값은 다음과 같이 간단하게 표현 가능합니다.

\[\mathbb{E} \left[ \rho_{t:T-1} G_t \right] = \mathbb{E} \left[ \tilde{G}_k \right],\] \[\text{where  } \tilde{G}_t = \rho_{t:t} R_{t+1} + \gamma \rho_{t:t+1} R_{t+2} + \gamma^2 \rho_{t:t+2} R_{t+3} + \cdots + \gamma^{T-t-1} \rho_{t:T-1} R_T\]

위와 같은 식을 Per-decision Importance Sampling이라고 부릅니다. 이렇게 $\bar{G}_t$를 사용하면 식 (5.5)와 같이 Bias가 없어지는 $V(s)$의 추정이 나오는데, 식은 다음과 같습니다. (First-visit 이라고 가정)

\[V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \bar{G}_t }{|\mathcal{T}(s)|} \tag{5.15}\]

식 (5.15)는 Ordinary Importance Sampling으로부터 유도된 Per-decision Importance Sampling입니다. 이와 비슷한 방법으로 Weighted Importance Sampling으로부터 Per-decision Importance Sampling을 유도할 수 있을 것 같지만, 대부분의 경우 일관성이 없기 때문에 (무한 개의 데이터가 주어졌을 때, 올바른 값으로 수렴하지 않음) 존재가 명확하지 않습니다.

Summary

이번 장에서 다룬 Monte Carlo Method는 Episode라는 경험을 통해 Value Function과 Optimal Policy를 학습합니다. 이것이 DP보다 우수한 장점으로는 ① Environment에 대한 Model이 없어도 Environment와의 상호 작용을 통해 최적의 Action을 학습할 수 있고, ② 시뮬레이션이나 Sample Model과 함께 사용할 수 있으며, ③ State의 작은 부분 집합에 집중하는 것이 쉽고 효율적이라는 것입니다. (8장 참고)

이번 장에서 다루지는 않았지만, 추후 소개할 4번째 장점으로는 Markov Property를 위반했을 때 문제가 작다는 것입니다. 이것은 후속 State의 추정한 Value를 기반으로 현재의 Value를 추정하지 않기 때문입니다. (=Bootstrapping하지 않기 때문입니다)

Monte Carlo Control은 4장에서 소개했던 Generalized Policy Iteration (GPI)를 기반으로 설계하였습니다. GPI는 Policy Evaluation과 Policy Improvement의 상호 작용 과정을 포함합니다. Monte Carlo Method는 Model을 사용하는 대신 해당 State에서 시작했을 때 얻을 수 있는 수익을 평균화함으로써 대안적인 Policy Evaluation 방법을 제공합니다. 또한 Environment의 Transition Probability를 필요로 하지 않고 Policy를 개선할 수 있기 때문에 Action-Value Function을 추정하는데 유리합니다.

Monte Carlo Control에서는 충분한 탐색을 할 수 있도록 유지하는 것이 중요한 이슈입니다. 왜냐하면 현재 시점에서 가장 좋아보이는 Action이 궁극적으로 최선의 Action이 아닐 수 있기 때문입니다. 이것을 해결하기 위해 처음으로 생각할 수 있는 방법은 Episode가 무작위 State-Action에서 시작한다고 가정하는 것입니다. 하지만 이러한 Assumption of Exploring Starts는 실제 상황에서 적용하기 어렵습니다. 따라서 이에 대한 대안으로 Episode를 탐색하며 Optimal Policy를 찾는 On-policy 방법과, Target Policy와 Behavior Policy를 구분하여 Optimal Policy를 찾는 Off-policy 방법이 있습니다.

Off-policy 방법은 Behavior Policy에 의해 생성된 데이터로부터 Target Policy의 Value Function을 학습합니다. 이 학습 방법은 다른 표본(Behavior Policy)으로부터 생성된 데이터를 학습(Target Policy)에 사용하므로 Importance Sampling을 사용하여 Return에 가중치를 두는 방식으로 값을 보정합니다. 이 때 사용하는 방법은 두 가지가 있는데, Ordinary Importance Sampling은 단순한 평균을 사용하지만, Weighted Importance Sampling은 Weighted Avaerage를 사용한다는 차이가 있습니다. Ordinary Importance Sampling은 추정값이 Bias되지 않는다는 장점이 있지만, Variance가 크고 심지어 무한할 수도 있는 단점이 있는 반면, Weighted Importance Sampling은 추정값이 Bias될지언정 항상 유한한 Variance를 가진다는 장점이 있습니다. Off-policy 방법은 개념적으로 단순하지만, Prediction과 Control 모두 불안정하며 발전 가능성이 있기 때문에 지속적으로 연구되고 있습니다.

5장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!