$n$-step Bootstrapping

이번 장에서는 5장에서 배운 Monte Carlo Method과 6장에서 배운 Temporal Difference (TD)를 융합하여 만든 새로운 방법을 소개합니다. Monte Carlo Method는 항상 Episode가 끝난 후에야 학습이 가능했고, TD는 1단계만 관찰하면 학습이 가능했습니다. 그렇다면 그 사이의 단계인 $n$번째 단계까지 관찰한 다음 학습을 하게 되면 조금 더 일반화된 학습이 가능하지 않을까하는 아이디어가 떠오르게 됩니다.

이렇게 $n$개의 시간 단계 동안 관찰한 후 학습에 반영하는 것을 $n$-step Bootstrapping이라고 합니다. TD은 경험이 즉각적으로 학습에 반영되지만, 때때로 조금 더 장기적인 관점에서 바라봐야하는 문제가 있습니다. 이런 관점에서 $n$-step Bootstrapping은 12장에서 배울 Eligibility Traces의 기반이 됩니다.

이번 장 역시 이전 장들과 마찬가지로, 먼저 Prediction을 알아본 다음에 Control을 다루는 순서로 진행됩니다. 즉, 먼저 $n$-step Bootstrapping으로 $v_{\pi}$를 추정한 후, Optimal Policy를 찾기 위한 Control 방법을 논의할 예정입니다.

$n$-step TD Prediction

Policy $\pi$를 사용하여 생성된 Sample Episode에서 $v_{\pi}$를 추정할 때, Monte Carlo Method는 Episode가 끝날 때까지 해당 State부터 관찰된 전체 Reward의 합인 Return을 기반으로 업데이트하고, 1-step TD는 1개의 Reward만 관찰한 후 업데이트합니다. 이번에는 이 두 극단적인 방법의 중간점으로 $n$개의 Reward를 관찰한 후 업데이트를 수행하는 $n$-step TD에 대해 알아보겠습니다. 1-step TD, $n$-step TD, 그리고 Monte Carlo Method의 차이는 아래의 Backup Diagram을 보시면 쉽게 이해할 수 있습니다.

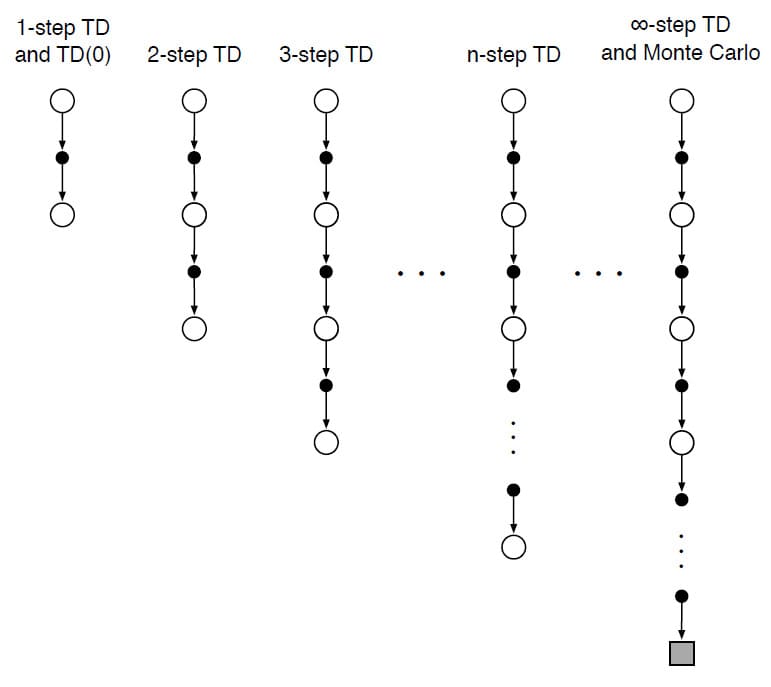
$n$-step 업데이트를 1-step TD와 마찬가지로 TD라고 부르는 이유는, 1-step TD처럼 이후의 추정이 어떻게 달라지는지에 따라 이전의 추정이 변하기 때문입니다. 다만 그 추정이 1-step 후가 아니라 $n$-step 후일 뿐입니다.

이들간의 차이를 수식으로 비교해봅시다. 먼저 Monte Carlo Method에서 Return $G_t$를 계산하는 식은 다음과 같았습니다.

\[G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots + \gamma^{T-t-1} R_T\]

위 식에서 $T$는 Episode의 마지막 시간 단계입니다. Monte Carlo Method에서는 Return을 각 시간 단계마다 받는 Reward에 Discount $\gamma$를 곱한 값의 합으로 계산합니다.

\[G_{t:t+1} \doteq R_{t+1} + \gamma V_t (S_{t+1})\]

반면에 1-step TD에서는 첫 번째 Reward와, 다음 State의 추정 Value에 Discount를 곱한 값의 합으로 계산됩니다. $V_t$는 시간 단계 $t$에서 추정한 $v_{\pi}$를 의미하며, $G_{t:t+1}$는 시간 단계 $t$부터 $t+1$까지 얻은 수익을 의미합니다. 이 개념을 확장하면 2-step의 Return은 다음과 같음을 알 수 있습니다.

\[G_{t:t+2} \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 V_{t+1} (S_{t+2})\]

위와 같은 방법으로 $n$-step의 Return을 만들면 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n V_{t+n-1} (S_{t+n}) \tag{7.1}\]

위 식에서 $n \ge 1$이고 $0 \le t < T - n$이라는 조건이 있습니다. 만약 $t + n \ge T$라면 $n$-step이 끝나기 전에 Episode가 끝난다는 이야기이므로 $T$ 이후의 항은 모두 0으로 처리하면 됩니다.

1-step에서 시간 단계 $t+1$에 도달해야 $t$에서의 Value Function을 업데이트 할 수 있던 것처럼, $n$-step 또한 시간 단계 $t+n$에 도달해야만 $t$에서의 Value Function을 업데이트 할 수 있습니다. 그렇기 때문에 $n$-step에서 가장 처음 학습을 하는 시간 단계는 $t+n$이 됩니다. 이 점을 반영하여 $V$의 업데이트 식을 정의하면 다음과 같습니다.

\[V_{t+n} (S_t) \doteq V_{t+n-1} (S_t) + \alpha \left[ G_{t:t+n} - V_{t+n-1} (S_t) \right], \quad 0 \le t < T \tag{7.2}\]

이 때, $S_t$ 이외의 State에서는 Value Function이 변하지 않습니다. 즉, 모든 $s \ne S_t$에 대해서 $V_{t+n} (s) = V_{t+n-1} (s)$입니다. 이것을 $n$-step TD라고 부릅니다. $n$-step TD의 모든 Episode에서는 처음 $n-1$ 시간 단계까지는 아무것도 변하지 않는데, 이를 보완하기 위해 각 Episode가 끝난 후 다음 Episode가 시작되기 전에 동일한 수의 추가적인 업데이트가 이루어집니다. 완전한 Pseudocode를 보시면 이것이 어떤 의미인지 이해가 되실 겁니다.

$n$-step Return은 Value Function $V_{t+n-1}$를 사용하여 $R_{t+n}$ 이후에 누락된 Reward를 보완합니다. $n$-step Return의 장점은 최악의 상황에서 $V_{t+n-1}$보다 $v_{\pi}$ 추정값이 더 낫다는 것입니다. 다시말해, $n$-step Return에서 가장 큰 오차는 $V_{t+n-1}$의 가장 큰 오차보다 $\gamma^n$ 배 만큼 작거나 같습니다. 이것을 수식으로 표현하면 다음과 같습니다.

\[\max_s \left| \mathbb{E}_{\pi} \left[ G_{t:t+n} | S_t = s \right] - v_{\pi} (s) \right| \le \gamma^n \max_s \left| V_{t+n-1} (s) - v_{\pi} (s) \right| \tag{7.3}\]

식 (7.3)은 모든 $n \ge 1$에 대해 성립합니다. 이것을 Error Reduction Property of $n$-step Returns라고 합니다. 이 수식 덕분에 모든 $n$-step TD 방법이 적절한 조건 하에 올바른 추정값으로 수렴한다는 것이 보장됩니다.

$n$-step Sarsa

이번에는 $n$-step과 Sarsa를 결합한 Control을 배우도록 하겠습니다. 새로 배우는 Sarsa와 구분하기 위해, 이전 장에서 배운 Sarsa를 1-step Sarsa, 또는 Sarsa(0)으로 표기하고, 이번 장에서 배우는 새로운 방법은 $n$-step Sarsa로 부르겠습니다. $n$-step Sarsa의 기본 개념은 아래의 Backup Diagram과 같습니다.

이를 기반으로 $n$-step Return을 재정의하면 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} \gamma^n Q_{t+n-1} (S_{t+n}, S_{t+n}), \quad n \ge 1, 0 \le t < T-n \tag{7.4}\]

물론 이전 Section에서 배운 대로 $t + n \ge T$라면 $G_{t:t+n} \doteq G_t$입니다. 식 (7.4)를 알고리즘에 맞게 수정하면 다음과 같습니다.

\[Q_{t+n} (S_t, A_t) \doteq Q_{t+n-1} (S_t, A_t) + \alpha \left[ G_{t:t+n} - Q_{t+n-1} (S_t, A_t) \right] \quad 0 \le t < T \tag{7.5}\]

$n$-step Return처럼 식 (7.5)도 모든 $s \ne S_t$, $a \ne A_t$에 대해 $Q_{t+n} (s, a) = Q_{t+n-1}$입니다. 즉, 학습하고 있는 State-Action 쌍을 제외하고는 $Q$ 값이 변하지 않습니다. 그렇기 때문에 $n$-step Sarsa라고 부르는 것입니다. $n$-step Sarsa의 완전한 Pseudocode은 다음과 같습니다.

$n$-step Sarsa의 장점은 1-step Sarsa보다 학습 속도가 빠르다는 점입니다. 아래 그림은 Grid World에서의 예시를 보여주고 있습니다. 첫 번째 그림과 같은 Episode에 대해, 1-step Sarsa는 가운데 그림처럼 마지막 State-Action 쌍에 대해서만 $Q$ 값의 업데이트가 일어납니다. 하지만 세 번째 그림을 보시면 10-step Sarsa는 Episode 뒤 10개의 State-Action 쌍이 모두 업데이트가 되는 장점이 있습니다. 즉, 하나의 Episode에서 더 많은 것을 학습할 수 있다는 장점이 있습니다.

$n$-step과 Expected Sarsa를 결합하는 방법도 동일합니다. 이에 대한 Backup Diagram은 $n$-step Sarsa의 Backup Diagram 맨 오른쪽에 나타나 있습니다. 주의할 점은 시간 단계 $t$부터 $t+n$까지 모두 평균값을 사용하는 것이 아니라, 마지막 단계에서만 평균값을 사용합니다. $n$-step Expected Sarsa의 Return 식은 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n \bar{V}_{t+n-1} (S_{t+n}) \quad t+n < T \tag{7.7}\]

마찬가지로 $t + n \ge T$인 경우에는 $G_{t:t+n} \doteq G_t$입니다. 또한 $\bar{V}_t (s)$는 State $s$의 Expected Approximate Value이고, 다음과 같이 정의됩니다.

\[\bar{V}_t (s) \doteq \sum_a \pi (a|s) Q_t (s, a) \quad \text{for all } s \in \mathcal{S} \tag{7.8}\]

식 (7.8)은 지금 뿐만이 아니라 다른 장에서도 사용되기 때문에 기억해두시는 것이 좋습니다. 또한 식 (7.8)에서 만약 State $s$가 마지막 State라면 $\bar{V}_t (s) $는 0으로 정의됩니다.

$n$-step Off-policy Learning

이번에는 Off-policy 학습의 $n$-step 버전을 배워보겠습니다. $n$-step 방법에서는 Return이 $n$ 단계에 걸쳐 생성됩니다. Off-policy에서 중요한 점은 Target Policy $\pi$와 Behavior Policy $b$가 구분되는 것인데, 이 때 두 Policy 간의 차이를 보정하기 위해 Importance Sampling을 사용하였습니다. 그렇다면 $n$-step 버전에서 두 Policy 간의 Weight를 어떻게 처리하는지 다음 식을 통해 살펴보겠습니다.

\[V_{t+n} (S_t) \doteq V_{t+n-1} (S_t) + \alpha \rho_{t:t+n-1} \bigg[ G_{t:t+n} - V_{t+n-1} (S_t) \bigg] \quad 0 \le t < T \tag{7.9}\]

식 (7.9)에서 $\rho_{t:t+n-1}$가 바로 Importance Sampling Ratio입니다. 5장에서 배운대로 Importance Sampling Ratio는 다음과 같이 계산합니다.

\[\rho_{t:h} \doteq \prod_{k=t}^{\min (h,T-1)} \frac{\pi (A_k | S_k)}{b (A_k | S_k)} \tag{7.10}\]

만약 Policy $\pi$에 의해 선택되지 않는 Action의 경우(즉, $\pi (A_k \mid S_k) = 0$)에는 $n$-step Return에 Weight를 0으로 주고 완전히 무시해야 합니다. 반대로 Policy $\pi$가 Policy $b$보다 더 높은 확률로 선택되는 Action의 경우에는 Weight가 증가합니다. 만약 두 Policy $\pi$와 $b$가 동일한 경우 Importance Sampling Ratio는 정확히 1이 됩니다. 따라서 식 (7.9)와 같은 업데이트 식이 유도된 것입니다.

이와 같은 방법으로, $n$-step Sarsa 또한 다음과 같이 Off-policy 방법으로 대체할 수 있습니다.

\[Q_{t+n} (S_t, A_t) \doteq Q_{t+n-1} (S_t, A_t) + \alpha \rho_{t+1:t+n} \left[ G_{t:t+n} - Q_{t+n-1} (S_t, A_t) \right] \tag{7.11}\]

여기서 Importance Sampling Ratio는 식 (7.9)의 $n$-step TD 보다 한 단계 늦게 시작하고 끝납니다. 왜냐면 Sarsa는 Q-learning과 달리 다음 Action을 선택한 후에 학습을 하기 때문입니다. 전체 Pseudocode는 다음과 같습니다.

$n$-step Expected Sarsa의 Off-policy 버전은 Importance Sampling Ratio만 약간 변형시키면 됩니다. $\rho_{t+1:t+n-1}$ 대신 $\rho_{t+1:t+n}$로 바꾼 다음 나머지는 동일합니다. (물론 Return 식은 식 (7.7)을 사용합니다)

Per-decision Methods with Control Variates

이전 Section에서 제시한 $n$-step Off-policy 방법은 간단하고 개념적으로 명확하지만, 그렇게 효율적인 방법은 아닙니다. 보다 정교하게 접근하는 방법은 Section 5.9에서 잠깐 소개한 Per-decision Importance Sampling을 사용해야 합니다. 이 접근 방식은 식 (7.1)과 같은 $n$-step Return을 다음과 같은 Recursive Form으로부터 시작합니다.

\[G_{t:h} = R_{t+1} + \gamma G_{t+1:h} \quad t<h<T \tag{7.12}\]

이 때, $G_{h:h} \doteq V_{h-1}(S_h)$입니다. Importance Sampling Ratio를 고려할 때, 만약 Policy $\pi$에서 시간 $t$에 방문하지 않는 Action에 대해서 $\rho_t$는 0입니다. 이렇게 계산하면 $n$-step Return 또한 0이되고, Target Policy에 대해 Variance가 높아지는 문제가 있습니다. 그렇기 때문에 여기서는 이보다 정교한 새로운 방법을 제안하며, Off-policy의 $n$-step Return을 다음과 같이 재정의합니다.

\[G_{t:h} \doteq \rho_t (R_{t+1} + \gamma G_{t+1:h}) + (1 - \rho_t) V_{h-1} (S_t) \quad t<h<T \tag{7.13}\]

식 (7.12)와 동일하게 $G_{h:h} \doteq V_{h-1}(S_h)$입니다. 식 (7.13)은 기존과 다르게 $\rho_t$가 0이라고 할지라도 Return이 0이 되지 않는 대신 기존 추정치인 $V_{h-1} (S_t)$와 동일해집니다. Importance Sampling Ratio가 0이라는 뜻은 Sample을 무시하라는 뜻이므로 추정치를 변경하지 않게 바꾼 것입니다. 이 때, 식 (7.13)에서 오른쪽 두 번째 항을 Control Variate라고 합니다. Importance Sampling Ratio의 기대값이 1이라면 추정값과 상관이 없으므로 Control Variate의 기대값은 0이 됩니다. 또한 식 (7.13)과 같은 Off-policy의 $n$-step Return 정의는 식 (7.1)과 같은 On-policy Return 정의를 엄격하게 일반화했다고 볼 수 있습니다. 실제로 식 (7.13)에서 $\rho_t$를 항상 1이라고 가정하면 식 (7.1)과 동일합니다. 식 (7.13)의 업데이트 식은 식 (7.2)를 그대로 사용하면 됩니다.

Action-Value 버전에서는 첫 번째 Action이 Importance Sampling에서 영향을 끼치지 않기 때문에 $n$-step Return의 Off-policy 정의는 약간 다릅니다. 식 (7.7)과 같이 Expectation Form으로도, 식 (7.12)와 같은 Recursive Form으로도 표현할 수 있기 때문에 두 가지 표현 방법을 모두 보여드리도록 하겠습니다. 다음 식은 Control Variate를 포함하였습니다.

\[\begin{align} G_{t:h} &\doteq R_{t+1} + \gamma \left( \rho_{t+1} G_{t+1:h} + \bar{V}_{h-1} (S_{t+1}) - \rho_{t+1} Q_{h-1} (S_{t+1}, A_{t+1}) \right) \\ \\ &= R_{t+1} + \gamma \rho_{t+1} \left( G_{t+1:h} - Q_{h-1} (S_{t+1}, A_{t+1}) \right) + \gamma \bar{V}_{h-1} (S_{t+1}), t < h \le T \tag{7.14} \end{align}\]

Recursive Form에서 $h < T$인 경우 $G_{h:h} \doteq Q_{h-1} (S_h, A_h)$로, $h \ge T$라면 $G_{T-1:h} \doteq R_T$로 끝납니다. 식 (7.5)와 결합하여 추정 알고리즘을 만들면 Expected Sarsa와 유사한 형태가 나옵니다.

지금까지 사용한 Importance Sampling은 Off-policy 학습을 가능하게 하지만 높은 Variance를 유발하기 때문에 Step-size parameter를 작게 설정해야 합니다. 다만 이로 인해 학습 속도는 느려질 수밖에 없습니다. 즉, Off-policy 방법은 On-policy 방법보다 학습 속도가 느립니다. 물론 이를 개선하기 위한 여러 연구가 진행되고 있습니다. 이번 Section에서 다룬 Control Variate가 그 예 중 하나이며, 이 외에도 Autostep (Mahmood, Sutton, Degris and Pilarski, 2012), Tian (Karampatziakis and Langford, 2010), Mahmood(2017; Mahmood and Sutton, 2015) 등이 방법이 제안되었습니다. 다음 Section에서는 또 다른 방법인 Importance Sampling을 사용하지 않는 Off-policy 학습 방법에 대해 다루어 보겠습니다.

Off-policy Learning Without Importance Sampling : The n-step Tree Backup Algorithm

6장에서 1-step  Q-learning과 Expected Sarsa를 배울 때 Importance Sampling을 사용하지 않는 방법에 대해 배웠습니다. 이를 $n$-step으로 확장한 방법으로 Tree-backup Algorithm이 있습니다.

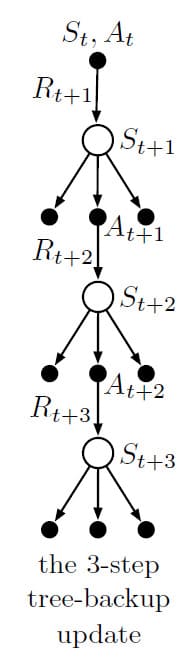
Tree-backup Algorithm의 기본 아이디어는 위의 Backup Diagram과 같습니다. Diagram의 각 단계에는 3가지 Sample State와 Reward, 그리고 2개의 Sample Action이 있습니다. 이것은 초기 State, Action 쌍인 $(S_t, A_t)$ 이후에 발생하는 이벤트를 나타냅니다. 각 State에서 가운데 Action을 제외한 나머지 Action은 선택되지 않은 Action입니다. 선택되지 않은 Action은 Sample 데이터가 없기 때문에 Bootstrap하고 Target Policy의 추정값을 업데이트하는데 사용합니다. 이것이 Backup Diagram처럼 나무 모양과 비슷하기 때문에 Tree-backup이라고 불립니다.

Tree-backup의 업데이트는 Tree의 Leaf Node로부터 추정된 Action-Value로부터 시작합니다. 각 Leaf Node는 Target Policy $\pi$로부터 선택될 확률에 비례하는 Weight를 기반으로 Target에 기여합니다. 따라서 첫 번째 Level의 Action은 $\pi (a \mid S_{t+1})$의 Weight로 기여하지만, 실제로 취한 Action $A_{t+1}$은 전혀 기여하지 않습니다. $\pi (A_{t+1} \mid S_{t+1})$은 두 번째 Level의 Action Value에 Weight를 부여하는데 사용됩니다. 즉, 선택되지 않은 두 번째 Level Action의 Weight는 $\pi (A_{t+1} \mid S_{t+1}) \pi (a’ \mid S_{t+2})$가 됩니다. 마찬가지로 세 번째 Level Action의 Weight는 $\pi (A_{t+1} \mid S_{t+1}) \pi (a’ \mid S_{t+2}) \pi (a’’ \mid S_{t+3})$이 됩니다. 쉽게 말해, Backup Diagram에서 각 Leaf Node가 의미하는 것은 Root State로부터 주어진 Policy $\pi$ 하에 해당 Action이 선택될 확률을 의미합니다.

3-step Tree-backup 업데이트는 각 State별로 가능한 모든 Action을 고려하는 과정과, 주어진 Policy에 따라 Action을 수행하는 과정이 포함되기 때문에 6개의 단계로 나눌 수 있습니다. 이것을 일반적인 $n$-step Tree-backup Algorithm으로 만들어보겠습니다. 먼저, 1-step의 Return은 다음과 같이 Expected Sarsa와 같은 모양으로 표현할 수 있습니다.

\[G_{t:t+1} \doteq R_{t+1} + \gamma \sum_a \pi(a | S_{t+1}) Q_t (S_{t+1}, a), \quad t < T-1 \tag{7.15}\]

같은 방식으로 2-step Tree-backup의 Return은 다음과 같습니다.

\[\begin{align} G_{t:t+2} & \doteq R_{t+1} + \gamma \sum_{a \ne A_{t+1}} \pi (a | S_{t+1}) Q_{t+1} (S_{t+1}, a) \\ \\ &+ \gamma \pi (A_{t+1} | S_{t+1}) \left( R_{t+2} + \gamma \sum_a \pi (a | S_{t+2}) Q_{t+1} (S_{t+2}, a) \right) \\ \\ &= R_{t+1} + \gamma \sum_{a \ne A_{t+1}} \pi (a | S_{t+1}) Q_{t+1}(S_{t+1}, a) + \gamma \pi (A_{t+1} | S_{t+1}) G_{t+1:t+2}, \quad t < T-2 \end{align}\]

이를 반복하여 일반적인 $n$-step Tree-backup Return의 Recursive Form은 다음과 같습니다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma \sum_{a \ne A_{t+1}} \pi (a | S_{t+1}) Q_{t+n-1} (S_{t+1}, a) + \gamma \pi (A_{t+1} | S_{t+1}) G_{t+1:t+n}   \tag{7.16}\]

단, $t < T - 1, n \ge 2$ 입니다. 만약 $n = 1$인 경우 식 (7.15)와 같으며, 예외적으로 $G_{T-1:t+n} \doteq R_T$입니다. 이것은 $n$-step Sarsa에서 다음과 같이 업데이트됩니다.

\[Q_{t+n} (S_t, A_t) \doteq Q_{t+n-1} (S_t, A_t) + \alpha \left[ G_{t:t+n} - Q_{t+n-1} (S_t, A_t) \right], \quad - \ge t < T\]

물론 학습에 사용되지 않는 모든 State $s \ne S_t$, 모든 Action $a \ne A_t$에 대해서는 Q 값이 변하지 않습니다. (즉, $Q_{t+n} (s, a) = Q_{t+n-1} (s, a)$) 전체 Pseudocode는 다음과 같습니다.

A Unifying Algorithm: $n$-step $Q(\sigma)$

지금까지 우리는 $n$-step Sarsa, $n$-step Tree-backup, 그리고 $n$-step Expected Sarsa에 대해 공부했습니다. 이 셋의 가장 큰 차이는 Sample로 인한 Importance Sampling의 여부입니다. $n$-step Sarsa는 매 단계마다 Importance Sampling Ratio를 보정해주어야 하고, $n$-step Expected Sarsa 또한 마지막을 제외한 모든 단계에서 Importance Sampling Ratio 보정이 필요합니다. $n$-step Tree-backup 알고리즘은 Importance Sampling이 필요없는 것이 특징입니다. 이번 Section에서는 이 3개의 알고리즘을 통합하는 방법을 알아보겠습니다.

기본적인 아이디어는 위의 그림에서 네 번째 Backup Diagram과 같습니다. 매 단계 Sarsa 처럼 처리할 것인지, 아니면 Tree-backup 처럼 처리할 것인지의 여부를 따로 정하는 것입니다. Expected Sarsa 처럼 처리하기 위해서는 마지막 단계를 Tree-backup 처럼 처리하면 됩니다.

단계 별로 어떻게 처리할 것인지는 $\sigma$의 값에 따라 달라집니다. $t$ 단계에서의 $\sigma$ 값을 $\sigma_t \in [0, 1]$라고 표기합니다. 만약  $\sigma = 1$인 경우 Sarsa와 동일해지고(=Full Sampling), $\sigma = 0$인 경우 Tree-backup과 동일해집니다(=Pure Expectation). 이 새로운 알고리즘을 $n$-step $Q(\sigma)$라고 합니다.

이제 $n$-step $Q(\sigma)$를 수식으로 표현해보겠습니다. 식 (7.16)의 Tree-backup $n$-step Return을 horizon $h = t + n$과 식 (7.8)의 $\bar{V}$로 표현합니다.

\[\begin{align} G_{t:h} &= R_{t+1} + \gamma \sum_{a \ne A_{t+1}} \pi (a | S_{t+1}) Q_{h-1} (S_{t+1}, a) + \gamma \pi (A_{t+1} | S_{t+1}) G_{t+1:h} \\ \\ &= R_{t+1} + \gamma \bar{V}_{h-1} (S_{t+1}) - \gamma \pi (A_{t+1} | S_{t+1}) Q_{h-1}(S_{t+1}, A_{t+1}) + \gamma \pi (A_{t+1} | S_{t+1}) G_{t+1:h} \\ \\ &= R_{t+1} + \gamma \pi (A_{t+1} | S_{t+1}) \left( G_{t+1:h} - Q_{h-1} (S_{t+1}, A_{t+1}) \right) + \gamma \bar{V}_{h-1} (S_{t+1}) \end{align}\]

그 이후로는 Importance Sampling Ratio $\rho_{t+1}$을 $\pi (A_{t+1} \mid S_{t+1})$로 대체한 것을 제외하고는 식 (7.14)와 같이 Control Variate가 있는 $n$-step Sarsa와 동일합니다. $Q(\sigma)$는 다음과 같이 표현할 수도 있습니다.

\[\begin{align} G_{t:h} & \doteq R_{t+1} + \gamma \left( \sigma_{t+1} \rho_{t+1} + (1 - \sigma_{t+1}) \pi (A_{t+1} | S_{t+1}) \right) \\ \\ &\times \left( G_{t+1:h} - Q_{h-1} (S_{t+1}, A_{t+1}) \right) + \gamma \bar{V}_{h-1} (S_{t+1}) \tag{7.17} \end{align}\]

이 때 $t < h \le T$ 입니다. Recursive Form에서 $h < T$인 경우 $G_{h:h} \doteq Q_{h-1} (S_h, A_h)$가 되고, $h = T$인 경우 $G_{T-1:T} \doteq R_T$가 됩니다. 그 후 식 (7.11) 대신 Importance Sampling Ratio가 없는 식 (7.5)를 사용하여 $n$-step Sarsa 업데이트를 사용합니다. Importance Sampling Ratio 자체가 $n$-step Return에 포함되기 때문입니다. $Q(\sigma)$의 완전한 Pseudocode는 다음과 같습니다.

Summary

이번 장에서는 1-step TD와 Monte Carlo Method의 중간으로 볼 수 있는 $n$-step TD에 대해 배웠습니다. 이렇게 극단적인 두 방법을 적절히 조절하여 중간 정도의 방법을 사용하는 것은 때때로 좋은 성능을 보입니다.

Section 7.6에서 사용했던 그림을 다시 가져와보면 이번 장에서 배운 내용이 요약되어 있습니다. $n$-step Sarsa나 Expected Sarsa는 기본적으로 Return을 계산할 때 Importance Sampling Ratio를 반드시 고려해야하며, 그 방법을 회피하기 위해 $n$-step Tree-backup을 고안하였습니다. 마지막으로는 이것들을 일반화할 수 있는 $n$-step $Q(\sigma)$를 제안하였습니다.

이러한 $n$-step 방법의 단점은 지난 장에서 배운 1-step 방법보다 각 시간 단계당 더 많은 계산이 필요할 뿐만 아니라 더 많은 메모리가 필요하다는 것입니다. 12장에서는 이 단점을 최소한으로 줄여 $n$-step TD를 구현하지만, 아무리 줄여도 항상 1-step보다는 계산량과 필요 메모리량이 많다는 한계가 있습니다. 하지만 이러한 단점을 감안하더라도 $n$-step 방법이 가지는 장점이(대표적으로 빠른 학습) 있기 때문에 고려할만한 가치는 있습니다.

Off-policy $n$-step은 추후 배울 Eligibility Traces보다 복잡하지만 개념적으로 명확하다는 장점이 있습니다. 이 장에서는 Off-policy $n$-step TD에 대해 2가지 방법으로 접근하였습니다. 첫 번째 방법은 기존에 배운 Importance Sampling을 이용하는 방법이었습니다. 이것은 개념적으로 간단하지만 Variance가 크다는 단점이 있습니다. 따라서 만약 Target Policy와 Behavior Policy가 매우 큰 차이가 나는 경우라면 이 방법은 적합하지 않습니다. 두 번째 방법으로 Tree-backup 방법을 제안하였습니다. 이것은 Stochastic Target Policy를 갖는 Q-learning을 $n$-step으로 확장한 개념입니다. Importance Sampling을 포함하지 않지만, Target Policy와 Behavior Policy의 차이가 클 경우 $n$이 크더라도 Bootstrapping이 간단하다는 장점이 있습니다.

7장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!