Temporal-Difference Learning

이번 장은 강화학습의 핵심 아이디어인 Temporal-Difference (TD) Learning을 다루게 됩니다. TD Learning은 Environment에 대한 정확한 Model 없이 경험을 통해 학습한다는 Monte Carlo의 아이디어와 Bootstrap 하지 않고 학습된 다른 추정치를 기반으로 추정치를 업데이트한다는 Dynamic Programming 아이디어를 결합하여 만들어졌습니다. 이번 장의 시작은 이전 장들과 같이 주어진 Policy $\pi$에 대한 Value Function $v_{\pi}$를 추정하는 문제로부터 시작하며, Optimal Policy을 찾는 Control 문제에서도 이전과 같이 GPI를 변형하여 접근합니다. 이전 장들과의 주요 차이점은 Prediction 문제에 대한 접근 방식입니다.

이번 장 이후로 나오는 대부분의 주제는 Dynamic Programming, Monte Carlo, TD Learning과 관련이 있으며, 특히 7장에서는 TD Learning과 Monte Carlo 방법의 중간 개념임 $n$-step Bootstrapping을 소개하고, 12장에서는 이것들을 매끄럽게 통합할 수 있는 TD($\lambda$)를 소개합니다.

TD Prediction

TD Learning과 Monte Carlo Method는 모두 경험을 사용하여 Value Function을 추정합니다. Monte Carlo 방법은 State를 방문 후, Return의 값을 알 수 있을 때까지 기다린 다음 그 값을 토대로 $V(S_t)$를 추정합니다. 간단한 Every-visit Monte Carlo Method의 $V(S_t)$ 업데이트 식은 이전 장에서 배운 대로 다음과 같습니다.

\[V(S_t) \gets V(S_t) + \alpha \left[ G_t - V(S_t) \right] \tag{6.1}\]

이전에 배운 대로 Return $G_t$는 시간 $t$ 이후에 얻는 기대 Reward이고, $\alpha$는 Step-size parameter 입니다. 만약 $\alpha$가 상수라면 식 (6.1)을 Constant-$\alpha$ Monte Carlo라고 부릅니다.

Monte Carlo Method에서는 $G_t$를 얻기 위해 Episode가 끝날 때까지 기다려야 하지만, TD Learning에서는 다음 시간 단계까지만 기다리면 된다는 차이가 있습니다. 시간 $t+1$에서 얻은 Reward $R_{t+1}$과 추정된 Value Function $V(S_{t+1})$을 사용하여 $V(S_t)$를 업데이트 할 수 있습니다. 가장 간단한 TD의 업데이트 식은 다음과 같습니다.

\[V(S_t) \gets V(S_t) + \alpha \left[ R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \right] \tag{6.2}\]

식 (6.2)와 같은 업데이트 식을 $TD(0)$, 또는 1-step TD 라고 부릅니다. 이렇게 부르는 이유는 추후 12장에서 다룰 $TD(\lambda)$와 7장에서 다룰 $n$-step TD의 특수한 형태이기 때문입니다. 아래는 $TD(0)$ 업데이트를 사용한 Value Function 추정 방법의 완전한 Pseudocode입니다.

TD(0) 알고리즘은 부분적으로 기존 추정값을 기반으로 업데이트 하기 때문에 DP와 같은 Bootstrapping 방법이라고 부를 수 있습니다. 또한 3장에서 다루었던 Value Function의 추정 식을 다시 가져와보면,

\[\begin{align} v_{\pi} & \doteq \mathbb{E}_{pi} \left[ G_t | S_t = s \right] \tag{6.3} \\ \\ &= \mathbb{E}_{pi} \left[ R_{t+1} + \gamma G_{t+1} | S_t = s \right] \tag{from (3.9)} \\ \\ &= \mathbb{E}_{pi} \left[ R_{t+1} + \gamma v_{\pi} (S_{t+1}) | S_t = s \right] \tag{6.4} \end{align}\]

식 (6.3)은 Monte Carlo Method가 Target으로 하는 추정값이고, 식 (6.4)는 DP가 Target으로 하는 추정값입니다. 두 식이 추정값인 이유는 Monte Carlo Method에서는 실제 Expected Return이 아닌 Sample Return이 사용되기 때문이고, DP에서는 $v_{\pi}(S_{t+1})$가 알려져 있지 않아 $V(S_{t+1})$를 대신 사용하기 때문입니다. TD의 Target은 Sample Return을 사용하며 역시 $V(S_{t+1})$를 사용하기 때문에 추정값이 됩니다. 즉, TD는 Monte Carlo Method와 DP를 결합한 것으로 볼 수 있습니다.

위의 그림은 TD(0)에 대한 Backup Diagram입니다. 맨 위의 흰 점은 State 노드를 의미하며, 이에 대한 추정값은 바로 다음 State만 사용하기 때문에 Backup Diagram이 간단하게 표현됩니다. TD와 Monte Carlo 방법은 Sample Update라고 부르는데, 그 이유는 현재 State에서 이어지는 Action과 Reward를 사용하여 원래의 State(또는 State-Action 쌍)를 업데이트하기 때문입니다.

마지막으로 TD(0)에서 0이 의미하는 것은 $S_t$의 추정값과 $R_{t+1} + \gamma V(S_{t+1})$의 추정값 사이의 차이입니다. 이것을 TD-error라고 하는데, 추후 배울 강화학습에서 다양한 형태로 만나보실 수 있습니다.

\[\delta_t \doteq R_{t+1} + \gamma V(S_{t+1}) - V(S_t) \tag{6.5}\]

각 시간 단계의 TD-error는 그 당시에 추정했던 값의 오차입니다. TD-error는 다음 State와 다음 Reward에 따라 달라지기 때문에 실제로는 다음 단계 전까지 사용할 수 없습니다. 즉, $\delta_t$는 $V(S_t)$에서 발생하는 오차이지만, $t+1$ 시간이 되어야 알 수 있습니다. 만약 $V$가 Episode가 끝나기 전까지 변경되지 않는다면 Monte Carlo의 오차 또한 TD-error의 합으로 표현할 수 있습니다. (다행히 Monte Carlo Method에서는 Episode가 끝나기 전까지 $V$가 변하지 않습니다)

\[\begin{align} G_t - V(S_t) &= R_{t+1} + \gamma G_{t+1} - V(S_t) + \gamma V(S_{t+1}) - \gamma V(S_{t+1}) \tag{from (3.9)} \\ \\ &= \delta_t + \gamma (G_{t+1} - V(S_{t+1})) \\ \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 (G_{t+2} - V(S_{t+2})) \\ \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t} (G_T - V(S_T)) \\ \\ &= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \cdots + \gamma^{T-t-1} \delta_{T-1} + \gamma^{T-t} (0 - 0) \\ \\ &= \sum_{k=t}^{T-1} \gamma^{k-t} \delta_k \tag{6.6} \end{align}\]

만약 $V$가 Episode 도중에 업데이트 되는 경우 위의 과정은 정확하지 않지만, Step-size가 작으면 대략적으로 근접할 수는 있습니다. 이 과정은 TD에서의 이론과 알고리즘에서 중요한 역할을 합니다.

Advantage of TD Prediction Methods

이번 Section에서는 TD가 Monte Carlo Method나 DP에 비해 어떤 이점이 있는지 알아보도록 하겠습니다. 가장 먼저 생각할 수 있는 TD의 장점은 DP와 달리 Environment의 Model이 필요하지 않다는 점입니다. 물론 이것은 Monte Carlo Method도 가지고 있는 장점이긴 합니다.

그렇다면 Monte Carlo Method에 비해 TD가 가지는 장점은 Incremental로 구현이 가능하다는 것입니다. Monte Carlo Method의 가장 치명적인 단점은 Episode가 끝날 때까지 기다려야 한다는 것입니다. Episode의 길이가 길다면 그만큼 학습하기 위해 대기해야하는 시간 또한 길어지게 됩니다. 지난 장에서 Episode를 일부 무시하거나 줄이는 방법들을 잠깐 소개하였으나, 이것들은 실험적인 방법이기 때문에 문제가 해결된다고 볼 수는 없습니다.

다만 TD에서 하나의 Sample만을 가지고 학습하는 것이 과연 올바른 값으로 수렴함을 보장하는지를 따져봐야 합니다. 다행히도 고정된 Policy $\pi$에 대해  Step-size parameter $\alpha$가 충분히 작고, 조건 (2.7)을 만족한다면 TD(0)은 확률 1로 $v_{\pi}$에 수렴합니다. 일반적인 상황에 대해서는 9.4에서 다룰 예정입니다.

TD와 Monte Carlo Method가 모두 수렴하는 것이 보장된다면, 다음으로 논의할 것은 어떤 것이 더 빨리 수렴하는가입니다. 안타깝게도 어떤 방법이 더 빠르게 수렴하는지는 수학적으로 증명되지 않았지만, 일반적으로는 TD가 Monte Carlo Method보다 빠르게 수렴한다고 합니다.

Monte Carlo Method와 TD의 장단점을 요약하면 다음과 같습니다.

Monte Carlo has high variance, zero bias

• Good convergence properties (even with function approximation)
• Not very sensitive to initial value
• Very simple to understand and use

Temporal-Difference has low variance, some bias

• Usually more efficient than Monte Carlo
• TD(0) converges to $v_{\pi}(s)$ (but not always with function approximation)
• More sensitive to initial value

Optimality of TD(0)

만약 10개의 Episode, 또는 100개의 시간 단계와 같이 제한된 숫자의 경험만 사용할 수 있다고 가정해봅시다. 이 경우 Incremental 학습 방법의 접근 방식은 수렴될 때까지 경험을 반복적으로 학습하는 것입니다. 문제는 Value Function $V$가 Episode 당 단 한번만 변경된다는 것입니다. (TD(0) 알고리즘 참고) 이렇게 전체 데이터를 사용하여 학습하고 수렴하도록 만드는 방법을 Batch Updating이라고 합니다.

배치 업데이트에서 TD(0)는 Step-size parameter $\alpha$가 충분히 작다는 조건 하에 답에 수렴합니다. Constant-$\alpha$ Monte Carlo Method도 동일한 조건에서는 수렴하지만, 다른 답으로 수렴합니다. 이것은 설명으로만 이해하기 어렵기 때문에, 교재에 나와있는 예제를 통해 보충하도록 하겠습니다.

Example 6.4) You are the Predictor

알 수 없는 MDP 문제에 대해 다음 8개의 Episode가 관찰되었다고 가정해보겠습니다.

• A, 0, B, 0
• B, 1
• B, 1
• B, 1
• B, 1
• B, 1
• B, 1
• B, 0

첫 번째 Episode는 State A에서 시작하여 0의 Reward를 받고 State B로 이동한 다음, 0의 Reward를 받고 종료된 것을 의미합니다. 나머지 Episode 중 6개는 State B에서 시작하여 1의 Reward를 받고 종료되고, 마지막 Episode는 State B에서 시작하여 0의 Reward를 받고 종료됩니다.

위의 8개의 Episode를 기반으로 Value $V(A)$, $V(B)$를 추정해봅시다. 먼저 State B를 보면 8개의 Episode 중 2개의 Episode가 0의 Reward를 받고, 6개의 Episode가 1의 Reward를 받으므로 $V(B) = 0.75$라고 쉽게 추정할 수 있습니다.

문제는 $V(A)$입니다. 주어진 Episode에서 State A가 언급된 것은 첫 번째 Episode 하나인데, 이것만으로 유추하자면 State A는 100% 확률로 0의 Reward를 받고 State B로 이동하는 것처럼 보입니다. 이것을 그림으로 표현하면 다음과 같습니다.

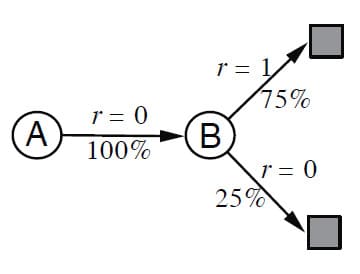
즉, State A의 Value는 $V(B)$와 동일하게 $V(A) = 0.75$라고 말할 수 있습니다. 이 결과는 Batch TD(0)로 계산해도 동일한 결과가 나옵니다.

또 다른 추정 방법은 8개의 Episode 중 State A는 단 한번 등장했고, 그 때의 Reward는 0이었으므로 $V(A) = 0$으로 추정하는 것입니다. 이 결과는 Batch MC와 동일한 결과입니다. 이렇게 추정하면 실제로 데이터에 대해서는 RMS Error가 0이 됩니다. (0으로 추정했는데 표본이 0이므로) 하지만 생각해봤을 때, $V(A) = 0$으로 추정하는 것 보다 $V(A) = 0.75$로 추정하는 것이 더 합리적으로 보입니다. 이를 토대로 결론을 내려보면, Monte Carlo 방법은 현재 주어진 데이터에서 더 우수한 성능을 보일 수 있지만, 미래에 얻게 될 데이터까지 고려한다면 TD(0)가 더 우수한 성능을 보일 것이라고 기대할 수 있습니다.

□

Example 6.4를 보시면 Batch TD(0)와 Batch MC로 찾은 추정치가 어떻게 다른지 알 수 있습니다. Batch MC는 항상 Training Data에서 Root Mean Square (RMS) Error를 최소화하는 추정치를 찾지만, Batch TD(0)는 항상 Maximum-likelihood Model에 맞는 추정치를 찾습니다. Batch TD(0)와 같이 추정하는 것을 Certainty-equivalence Estimate 라고 합니다.

Certainty-equivalence Estimate은 확실히 최적의 해법처럼 보이지만, 일반적인 상황에서는 위의 Example 6.4와 같이 직접 Value Function를 계산하는 것이 현실적으로 어렵다는 문제점이 있습니다. $n$을 State의 수라고 하면(즉, $n = \lvert \mathcal{S} \rvert$), Maximum-likelihood Model을 추정하는데 $n^2$의 메모리가 필요하고, Value Function를 계산하는 데 $n^3$ 만큼의 시간 단계가 필요합니다. 이러한 측면에서 보면 TD(0)는 Example 6.4와 같이 직접 계산하지 않고도 훨씬 적은 메모리와 시간을 소모하여 이와 동일한 답으로 수렴하기 때문에 우수한 방법임을 알 수 있습니다.

Sarsa : On-policy TD Control

이제는 TD를 사용한 Control 방법에 대해 알아보겠습니다. 이전 장들과 마찬가지로 Control은 Generalized Policy Iteration (GPI)를 기반으로 하며, Evaluation과 Improvement에 TD를 사용합니다. Monte Carlo Method와 마찬가지로 Exploration과 Exploitation 사이의 Trade-off가 있으며 그 때와 동일하게 On-policy와 Off-policy라는 두 가지 방법으로 나누어 접근합니다. 이번 Section에서는 먼저 On-policy를 사용한 TD Control 방법을 다룹니다.

첫 번째 단계로는 State-Value Function가 아닌 Action-Value Function를 배우는 것입니다. 즉, 모든 State $s$와 Action $a$에 대하여, Policy $\pi$를 기반으로 $q_{\pi} (s, a)$를 추정합니다. 각각의 Episode는 다음과 같이 State와 State-Action이 반복적으로 이어져 있습니다.

지금까지는 계속 State에 대한 Value Function만을 고려했으나, 이번 Section부터는 State-Action 쌍에 대한 Value를 측정하기 때문에 $V(S)$가 아니라 $Q(S, A)$를 사용합니다. 이 부분을 제외하고는 식 자체가 크게 다르지 않고, 수렴 역시 동일하게 보장됩니다. TD(0)에서의 Q 값을 업데이트 하는 식은 다음과 같습니다.

\[Q(S_t, A_t) \gets Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right] \tag{6.7}\]

이 업데이트는 마지막 State가 아닌 모든 State $S_t$마다 수행됩니다. 만약 $S_{t+1}$이 마지막 State라면 $Q(S_{t+1}, A_{t+1})$는 0으로 정의됩니다. 이 업데이트를 사용하기 위해서 필요한 요소는 $S_t, A_t, R_{t+1}, S_{t+1}, A_{t+1}$ 5가지입니다. 그렇기 때문에 이 업데이트를 사용한 TD 제어를 Sarsa라고 부릅니다. Sarsa의 Backup Diagram은 아래와 같습니다.

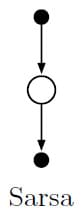
Sarsa는 이전에 배운 On-policy 방법과 마찬가지로 Policy $\pi$에 대해 $q_{\pi}$를 추정하고, $q_{\pi}$에 대해 greedy하게 $\pi$를 변경하는 과정을 반복합니다. 전체 Sarsa 알고리즘의 Pseudocode는 다음과 같습니다.

Sarsa의 수렴성은 Q에 대한 Policy의 조건이 어떤 지에 따라 다릅니다. $\epsilon$-greedy을 사용하는 것과 상관 없이, Step-size에 대한 조건인 식 (2.7)을 만족하고, 모든 State-Action 쌍이 무한한 횟수로 방문되는 조건 하에 확률 1로 Optimal Policy 및 Action-Value Function으로 수렴합니다.

Q-learning : Off-policy TD Control

Off-policy TD Control 학습 알고리즘은 Q-learning이라는 이름으로 불립니다. Q-learning은 강화학습 중에서도 가장 유명한 학습 방법이며, 1989년에 Chris Watkins 교수님이 처음 제안한 방법입니다. Q-learning의 업데이트 식은 다음과 같습니다.

\[Q(S_t, A_t) \gets Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \max_a Q(S_{t+1}, a) - Q(S_t, A_t) \right] \tag{6.8}\]

식 (6.8)은 Sarsa의 업데이트 규칙인 식 (6.7)과 대부분 유사합니다. 딱 한부분만 다른데, 다음 State와 Action을 사용했던 Sarsa와 달리 Q-learning은 다음 State에서 가능한 Action 중 Q값이 가장 큰 Action을 현재의 Q 값에 반영한다는 것입니다. Off-policy는 Behavior Policy와 Target Policy가 구분되기 때문이라고 이해하시면 되겠습니다. Q-learning의 전체 Pseudocode는 다음과 같습니다.

Example 6.6) Cliff Walking

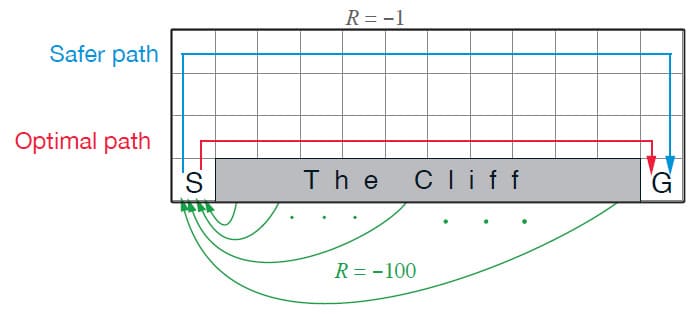
Sarsa와 Q-learning의 차이를 한 눈에 알 수 있는 예제로 Cliff Walking이라는 문제가 있습니다. 위와 같이 Gridworld로 구성된 Environment에서 Episode는 S라는 위치에서 시작하고, G에 도달하는 것이 목표입니다. Cliff State의 Reward는 -100로, 나머지 모든 State에서의 Reward는 -1로 정의되어 있습니다. 만약 Agent가 Cliff나 G에 도달하면 Episode가 종료됩니다.

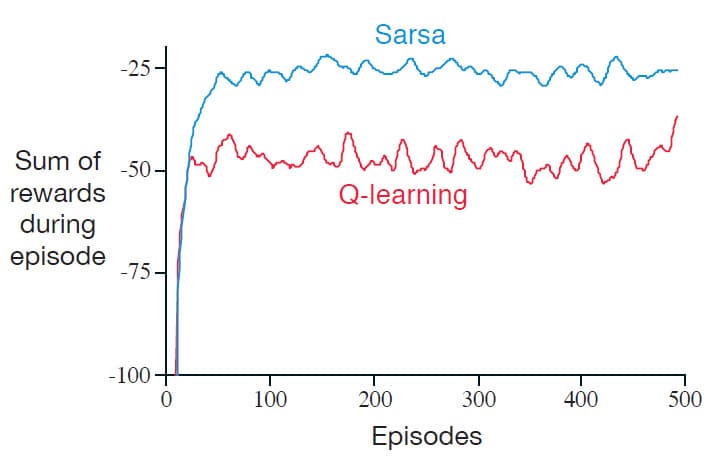
위의 그래프는 $\epsilon = 0.1$으로 설정한 $\epsilon$-greedy Policy를 사용했을 때 Sarsa와 Q-learning의 성능을 비교한 그림입니다.  Q-learning은 Cliff의 가장자리를 따라 이동하는 Policy로 수렴하지만, 때때로 $\epsilon$-greedy로 인해 Cliff State에 진입하는 경우가 발생합니다. 반면에 Sarsa는 Cliff에 최대한 접근하지 않도록 안전한 경로로 학습하기 때문에, Cliff에 떨어지는 경우는 발생하지 않지만 최적의 경로보다 우회한 경로로 수렴하게 됩니다.

□

Expected Sarsa

이번 Section부터는 Sarsa와 Q-learning으로부터 파생된 방법을 하나씩 다룰 예정입니다. 먼저 Sarsa를 변형한 Expected Sarsa 방법이 있습니다. Expected Sarsa는 이름과 같이 (다음 State Q 값의) 평균을 사용한 방법입니다. Expected Sarsa의 업데이트 식은 다음과 같습니다.

\[\begin{align} Q(S_t, A_t) & \gets Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \mathbb{E}_{\pi} \left[ Q ( S_{t+1}, A_{t+1} ) | S_{t+1} \right] - Q(S_t, A_t) \right] \\ \\ &= Q(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma \sum_a \pi (a | S_{t+1}) Q(S_{t+1}, a) - Q(S_t, A_t) \right] \tag{6.9} \end{align}\]

교재에서는 다음 State $S_{t+1}$이 주어졌을 때, Sarsa의 Expectation대로 이동하기 때문에 Expected Sarsa라는 이름이 붙었다고 합니다. 어차피 비슷한 의미이니 다음 State의 평균 Q 값을 사용하기 때문에 Expected Sarsa라는 이름이 붙었다고 이해해도 괜찮을 것 같습니다.

Expected Sarsa는 Sarsa보다 계산이 더 복잡하지만, Sarsa에서 $A_{t+1}$을 무작위로 선택하기 때문에 발생하는 Variance가 없어진다는 장점이 있습니다. 이로 인해 동일한 학습량을 놓고 비교했을 때, Expected Sarsa는 Sarsa보다 약간 더 나은 성능을 보입니다. 아래의 그래프는 Cliff Walking 예제에서 Sarsa, Q-learning, Expected Sarsa 간의 성능을 비교한 그림입니다. Interim Performance에서 Expected Sarsa는 다른 두 방법보다 더 우수한 성능을 보일 뿐만 아니라, Asymptotic Performance에서 성능이 하락하는 Sarsa에 비해 성능 저하 없이 우수한 성능을 유지하는 모습을 보여줍니다.

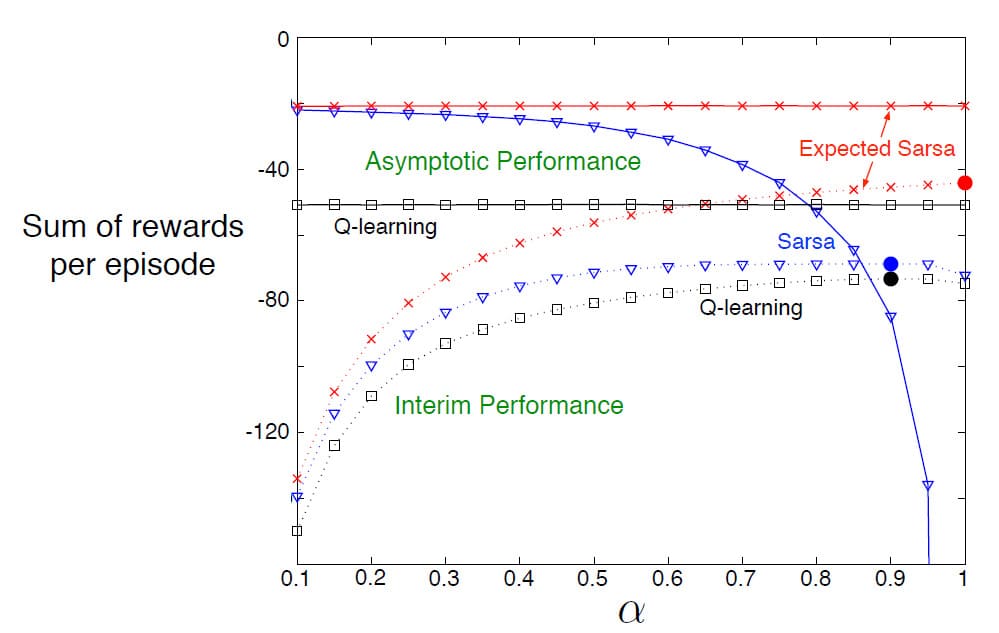
Cliff Walking 예제에서는 Expected Sarsa가 On-policy로 구현되었지만, Q-learning처럼 Behavior Policy와 Target Policy를 분리하여 Off-policy로 구현할 수도 있습니다. 이 경우 Expected Sarsa는 Q-learning과 거의 동일해지며, 추가적인 계산량만 감당할 수 있다면 대부분의 TD 알고리즘보다 더 우수한 성능을 보인다는 장점이 있습니다.

Q-learning와 Expected Sarsa의 Backup Diagram을 비교하면 위와 같습니다. 두 방법 모두 다음 State의 모든 Action을 고려하는 것은 같으나, Q-learning은 다음 State에서 가능한 Action 중 가장 Q 값이 높은 Action만을 찾아 학습에 반영하는 반면에, Expected Sarsa는 다음 State에서 가능한 Action을 모두 고려하여 Q 값의 평균을 계산한 다음 학습에 반영한다는 차이점이 있습니다.

Maximization Bias and Double Learning

지금까지 배운 Control 방법들은 Target Policy를 최적화하는데 중점을 두었습니다. 만약 추정한 값보다 최대값이 큰 경우, 이 값은 최대값의 추정값으로 사용될 수 있으며, 이로 인해 상당한 Bias를 초래할 수 있습니다. 예를 들어, 실제 $q(s, a)$ 값은 모두 0이라고 가정한 상황에서, 추정값 $Q(s,a)$가 불확실하므로 0보다 클 수도 있고 0보다 작을 수도 있습니다. 이 경우 실제 $q(s, a)$ 값의 최대값은 0이지만, 추정값 $Q(s,a)$의 최대값은 양수입니다. 즉, 양의 방향으로 Bias되었다고 볼 수 있습니다. 이것을 Maximization Bias라고 합니다. 구체적인 예시를 통해 이것이 어떻게 발생하는지 살펴보도록 하겠습니다.

Example 6.7) Maximization Bias Example

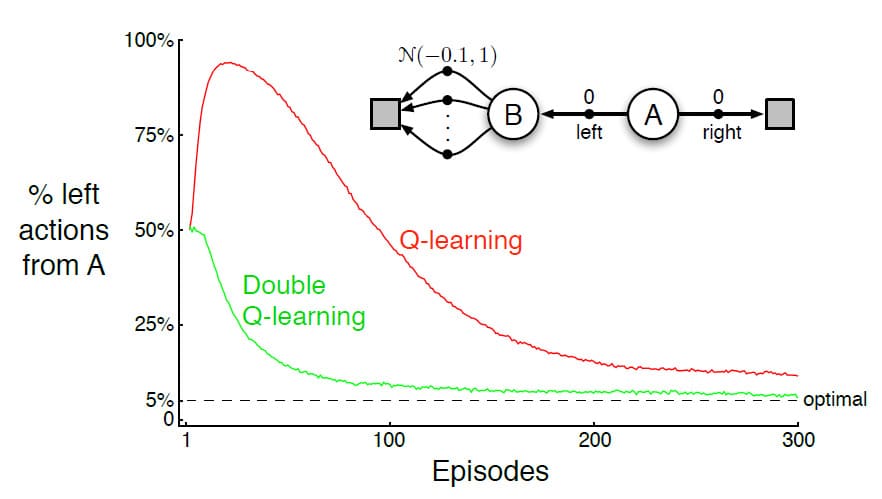
위의 그림은 Maximization Bias가 TD Control에서 어떻게 문제를 발생시키는지 알 수 있는 간단한 예제입니다. 예제의 MDP는 항상 State A에서 Episode가 시작됩니다. 왼쪽 끝, 또는 오른쪽 끝 State에 도달하면 Episode가 종료됩니다. State A에서 오른쪽으로 갈 때는 0의 Reward를 받지만, B에서 왼쪽으로 갈 때는 정규분포 $N(-0.1, 1)$에 따른 Reward를 받습니다. 왼쪽으로 갈 때의 평균 Reward는 -0.1이기 때문에, Reward가 0으로 고정된 오른쪽에 비해서 좋지 않은 방향임을 쉽게 알 수 있습니다. 문제는 왼쪽의 Reward가 정규분포를 따르기 때문에, 0보다 큰 Reward를 받을 확률이 있다는 것입니다. 그렇기 때문에 학습량이 적은 초기에는 왼쪽으로 가는 것을 더 좋은 Action으로 학습하게 되고, 그것이 위의 그래프에 나타나 있습니다. (Q-learning이 초기에 왼쪽을 선택학 확률이 매우 높음)

□

Maximization Bias를 피하기 위한 대표적인 방법으로 Double Q-learning이 있습니다. Agent를 2개로 나누어 각각 따로 학습하는 것입니다. 즉, Q 값을 2개로 분리하여 각각 $Q_1(a)$와 $Q_2(a)$로 나누는 것입니다. 두 개의 Q 값은 모두 $q(a)$의 추정치가 됩니다. 재밌는 것은 각각의 Agent가 Action을 선택할 때 상대의 추정값을 사용한다는 것입니다. 즉, $Q_2(A^{*}) = Q_2(\underset{a}{\operatorname{argmax}} Q_1(a))$가 되는 것입니다. 이렇게 추정값을 계산하게 되면 $\mathbb{E} \left[ Q_2 (A^{*}) \right] = q(A^{*})$라는 의미가 되어 Bias되지 않습니다. 마찬가지로 $Q_1$의 최적의 Action 선택 방식은 $Q_1(A^*) = Q_1(\underset{a}{\operatorname{argmax}} Q_2(a))$이 됩니다. 주의할 점은, 두 개의 추정을 따로 학습하지만, 각각의 Action마다 $Q_1$ 또는 $Q_2$ 중 하나의 추정치만 업데이트한다는 것입니다. 따라서 Double Q-learning은 공간 복잡도를 2배로 늘리지만, 시간 복잡도를 늘리지는 않습니다. 즉, 새로운 Action 샘플이 들어오면, 50% 확률로 $Q_1$을 학습하고, 50% 확률로 $Q_2$를 학습하는 것입니다. Double Q-learning의 업데이트 식은 다음과 같습니다.

\[Q_1(S_t, A_t) \gets Q_1(S_t, A_t) + \alpha \left[ R_{t+1} + \gamma Q_2 (S_{t+1}, \underset{a}{\operatorname{argmax}} Q_1(S_{t+1}, a)) - Q_1(S_t, A_t) \right] \tag{6.10}\]

식 (6.10)에서 $Q_2$를 학습할 때는 $Q_1$과 $Q_2$의 위치를 서로 바꾸면 됩니다. Double Q-learning에 대한 완전한 Pseudocode는 아래와 같습니다.

Double Q-learning과 Q-learning에 대한 성능 비교는 예제 6.7의 그래프를 확인해보시면 됩니다. 기존 Q-learning과 비교했을 때, 우연히 발생한 양의 Reward 쪽으로 Bias되지 않는 것을 볼 수 있습니다. 여기서는 Double Q-learning만 소개했으나, Sarsa와 Expected Sarsa를 응용해서 구현할 수도 있습니다.

Games, Afterstates, and Other Special Cases

1장에서 잠깐 다루었던 Tic-Tac-Toe 예제를 다시 떠올려봅시다. 그 당시에도 TD에 대해 잠깐 소개했었는데, 다시 그 부분을 확인해보시면 Tic-Tac-Toe에서는 Agent가 이동한 후 보드의 State를 평가했었습니다. 이렇게 Action을 먼저 한 후 State의 Value를 확인하는 것을 Afterstates라고 하고, 이 때의 Value Function를 Afterstate Value Function이라고 합니다. Afterstates는 Environment에 대한 초기 지식이 있지만, 전체 지식은 없고 일부분에 대한 지식만 있을 때 유용합니다. 예를 들어, 체스 같은 게임에서는 말을 움직였을 때 어떤 효과가 일어나는지는 바로 알 수 있지만, 상대방이 어떻게 행동할지는 모릅니다. Afterstates는 이런 종류의 지식을 활용하여 보다 효율적인 학습을 하는 방법이라고 이해하시면 되겠습니다.

Afterstate가 더 효율적인 것을 보이기 위해 다시 Tic-Tac-Toe 예제를 사용해보겠습니다. 기존의 Action-Value Function는 현재 O/X가 체크된 State를 토대로 Value를 추정합니다. 하지만 다음 그림을 보시면 현재 State가 될 수 있는 이전 State는 한 가지가 아닐 수 있습니다. 그러나 두 State는 모두 같은 후속 State를 만들기 때문에 동일하게 평가해야 합니다. 기존의 Action-Value Function는 두 State를 개별적으로 평가하지만, Afterstate Value Function는 두 State를 동등하게 평가하는 차이점이 있습니다. 즉, 아래 그림에서 왼쪽에서 발생하는 모든 학습은, 오른쪽 State에도 즉시 적용됩니다.

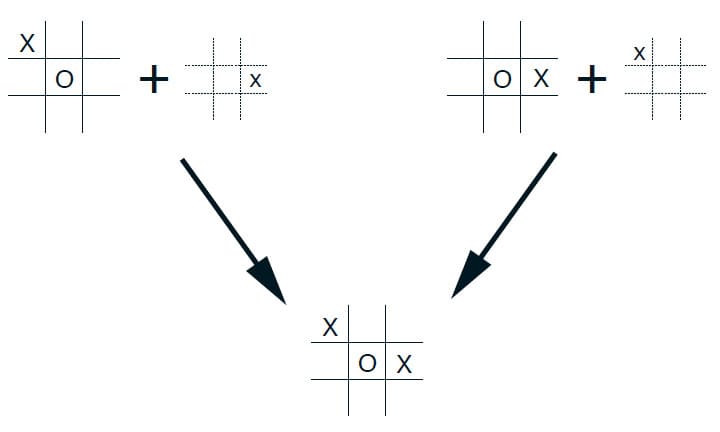
Afterstate는 게임에서만 사용되는 것이 아닙니다. 예를 들어, Queuing 문제에서는 Queue에 있는 작업을 서버에 할당하는지/거부할 것인지 등을 계속 판단해야 하는데, 동일한 작업에 대해서 동일하게 판단해야하므로 Afterstates를 적용할 수 있습니다. 이 외에도 Afterstates를 사용하는 여러 문제가 있지만, 여기서 모두 소개하기에는 불가능합니다. Afterstates는 동일한 방식으로 상호 작용하는 State 및 Policy에 대해서는 동일하게 추정해야하는 문제에 적용하는 것이라고 이해하시면 되겠습니다.

Summary

이번 장에서는 새로운 학습 방법인 Temporal Difference (TD)를 소개하였습니다. 이전 장들과 마찬가지로 예측 문제와 제어 문제로 나누어 소개하였으며, TD 또한 Generalized Policy Iteration 아이디어에서 기반하였습니다.

TD의 Control 방법 또한 On-policy와 Off-policy 방법으로 나뉘며, On-policy TD는 Sarsa, Off-policy TD는 Q-learning이라는 대표적인 방법을 소개하였습니다. 그 외에 Expected Sarsa나 Double Q-learning등의 변형 버전도 소개하였습니다. 이번 장에서 소개하지 않은 방법으로 Actor-Critic이 있는데, 이는 13장에서 자세히 다룰 예정입니다.

TD는 지금까지 배운 강화학습 방법 중에 가장 널리 사용되는 방법입니다. Dynamic Programming이나 Monte Carlo Method 등과 비교해서 단순할 뿐만 아니라 계산량 또한 적기 때문입니다. 이 뒤에 이어지는 내용들은 대부분 TD를 심도 있게 확장하여 더 강력하게 만든 알고리즘을 소개할 예정입니다. 특히 Part II 부터는 TD와 기존의 전통적인 기계학습 방법들을 융합한 새로운 학습 방법들을 소개합니다.

6장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!