VC Dimension

7장에서는 지난 장 마지막에 배운 Vapnic-Chervonenkis (VC) Dimension에 대해 자세히 알아보겠습니다.

Outline

이번 장은 4개의 소주제로 나뉘어 있습니다. 먼저 VC Dimension의 정의를 배우고, Perceptron에서의 VC Dimension이 어떻게 되는지 예제를 통해 알아봅니다. 세 번째로는 VC Dimension이 수학적으로/기계학습에서 어떤 의미를 가지는지 알아보고 마지막으로는 Hoeffding’s Inequality를 변형한 VC Inequality에서 각종 변수의 상한/하한점을 찾게 됩니다.

The definition

5장에서 배웠던 Break Point의 개념을 기억하고 계신다면 VC Dimension의 정의를 배우는 것은 어렵지 않습니다. Break Point $k$의 정의는 데이터를 흩뿌릴 수 없는, 다시말해 어떻게 데이터를 배치해도 Growth Function이 $2^k$보다 작은 $k$를 의미했습니다. VC Dimension은 이와 유사하게, 최대로 데이터를 흩뿌릴 수 있는 $k$를 의미합니다. 즉, Break Point - 1 = VC Dimension 입니다. VC Dimension은 $d_{VC}$로 표기합니다.

비교를 위해, 지난 시간에 Growth Function이 다항함수임을 증명했을 때 배운 식으로 Break Point와 VC Dimension의 표기 차이를 비교해보면 단순히 $k-1$이 $d_{VC}$로 치환되었음을 알 수 있습니다. 즉, 최고차 항의 지수는 $d_{VC}$까지 나올 수 있습니다. (최대 지수를 의미하는 것이지, 항상 $d_{VC}$가 최대임을 의미하는 것이 아닙니다.)

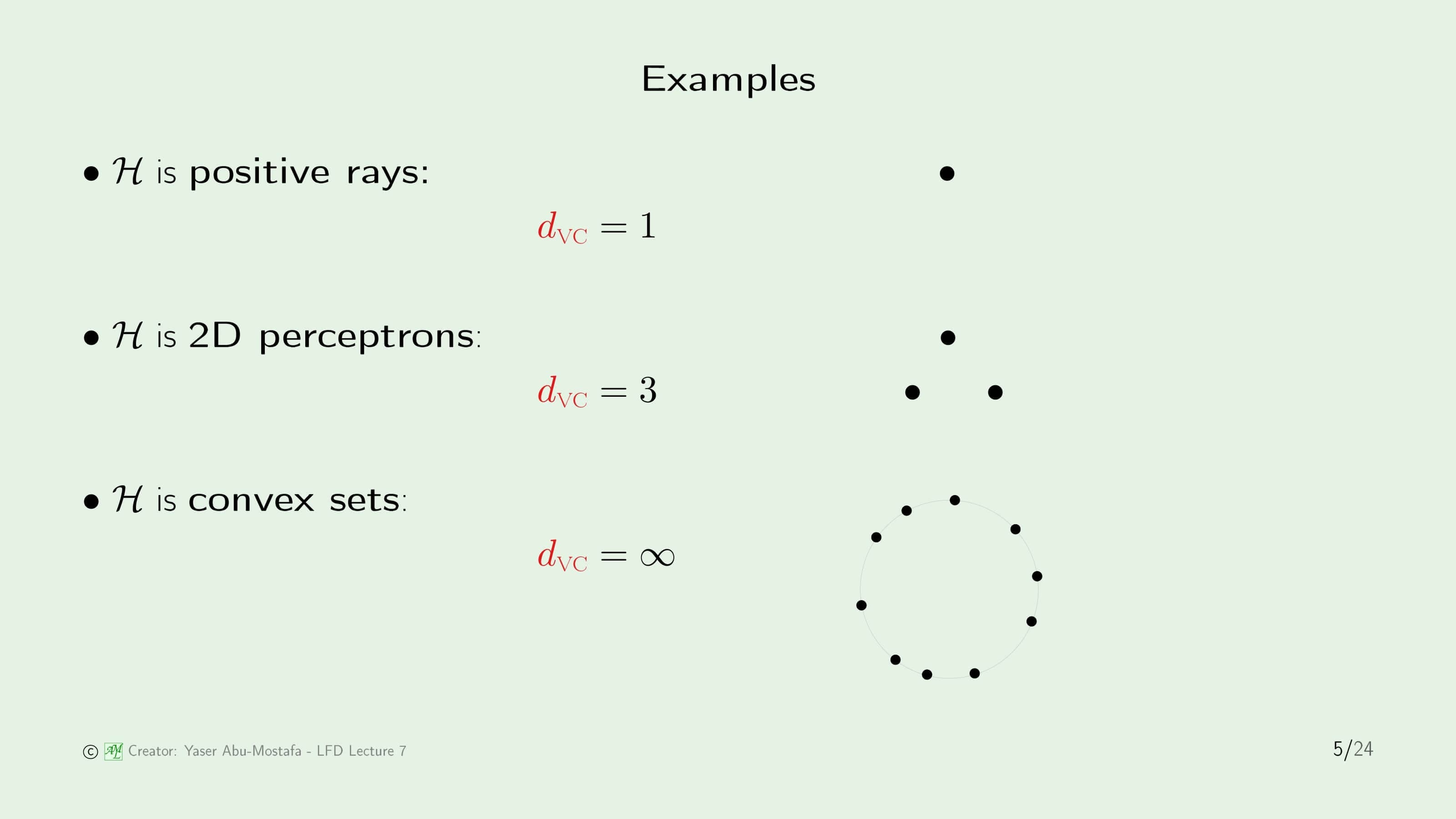
간단한 예제를 통해 VC Dimension을 구해봅시다. 첫째로 Positive Ray는 특정한 점을 기준으로 한쪽은 모두 -1, 다른 쪽은 모두 +1로 분류하였습니다. 이 때의 Growth Function이 $N+1$이었으므로 Break Point는 $k=2$가 됩니다. VC Dimension은 Break Point보다 하나 작은 값이기 때문에 $d_{VC}=1$임을 쉽게 알 수 있습니다. 두 번째 2D Perceptron도 마찬가지로 Break Point $k=4$이었기 때문에 $d_{VC}=2$가 되고, 마지막으로 Convex Set의 경우 Break Point가 무한대(Infinite)였기 때문에 VC Dimension 역시 무한대가 됩니다.

그렇다면 VC Dimension이 Learning에 어떤 관계가 있는지 알아봅시다. 가장 먼저, VC Dimension이 유한하다는 뜻은 곧 최종 가설 $g$이 일반화된다는 뜻입니다. (오른쪽 그림에서의 초록색 부분) 또한 Learning Algorithm, Input Distribution, Target Function에 독립적이기 때문에 이들을 고려할 필요가 없습니다. 다만 Hypothesis Set은 VC Dimension을 정의하기 위해 필요하기 때문에 독립적이지 않습니다. Tranining Example 또한 일반화에 필요하므로 무시할 수 없습니다. 이들은 추후 VC Inequality에 다시 등장하게 됩니다.

VC dimension of perceptrons

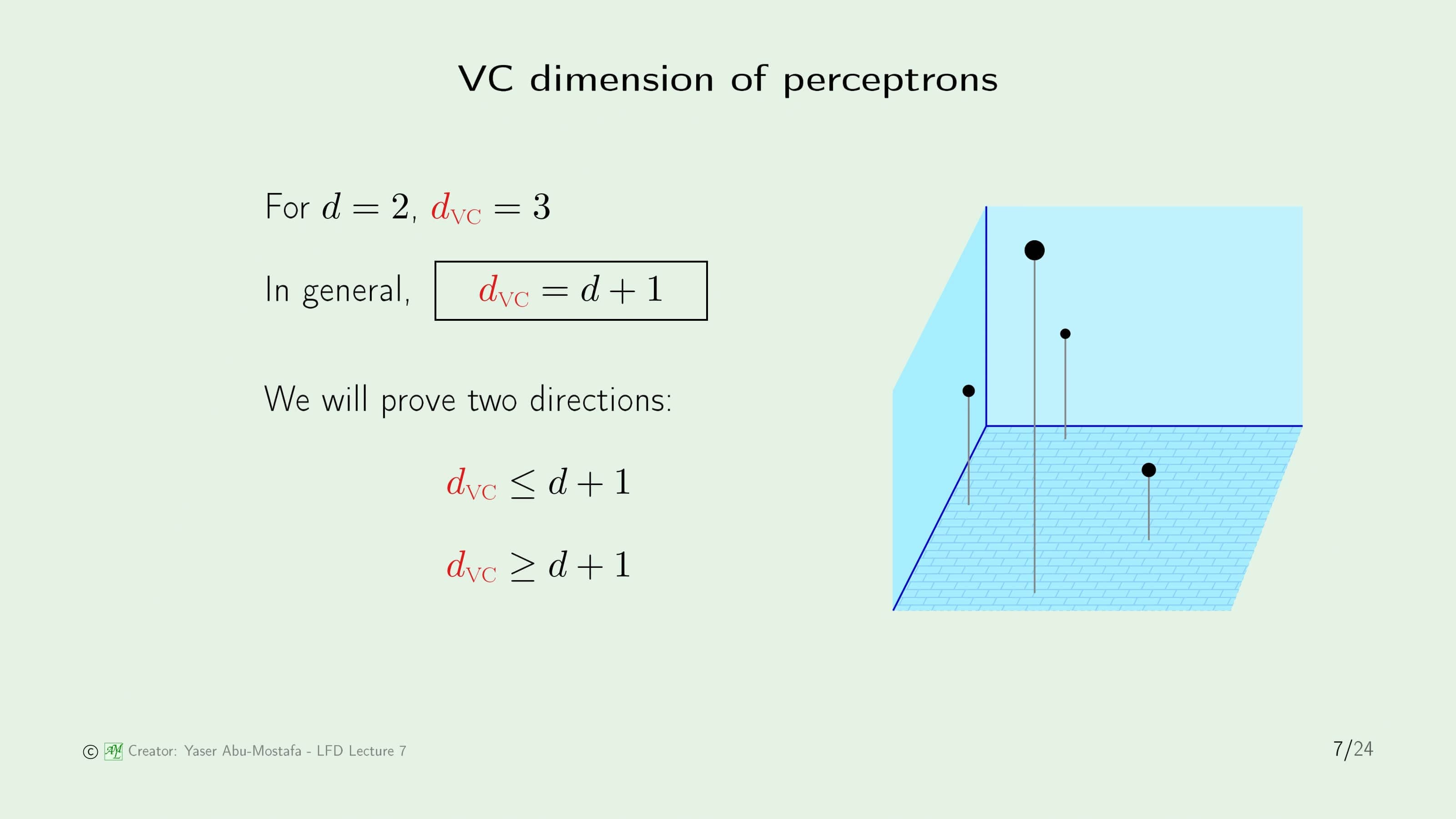
앞의 예제들을 통해 특수한 경우의 VC Dimension 값을 구했지만, 제대로 사용하기 위해서는 Growth Function을 배웠을 때처럼 일반항이 필요합니다. 일반적으로 VC Dimension의 값은 데이터의 차원 + 1과 같은데, 그 증명이 그렇게 어려운 편이 아니기 때문에 강의에서도 짚고 넘어갑니다. 증명을 스킵하실 분들은 16번 슬라이드로 바로 건너뛰셔도 됩니다.

증명의 방법은 두 집합이 같은 것을 증명하는 방법과 유사합니다. 일반적으로 A, B 두 집합이 같음을 증명할 때는 A 집합이 B 집합에 포함되는 것을 증명하고, B 집합이 A 집합에 포함된다는 것을 보이는 방법으로 증명하는데, 여기에서도 먼저 $d_{VC}$가 데이터의 차원 + 1보다 이상이라는 것과 이하라는 것을 각각 보여 둘을 합치는 방식으로 같음을 증명합니다.

먼저 $d$ 차원을 갖고 있는 $d+1$개의 점을 준비합니다. $d$ 차원이지만 Perceptron에서 항상 0번째 원소는 Threshold로 배정을 해 두었기 때문에 8번 슬라이드와 같이 Transpose를 사용해 $d+1$개의 점을 하나의 행렬 $X$로 만든다면 정사각 행렬이 됩니다. (첫 번째 열이 모두 1인 이유는 Threshold에 사용한 0번째 원소가 Transpose로 들어갔기 때문입니다.) 나머지 점들은 선형 독립이 되도록 배치하게 된다면 행렬 $X$는 역행렬이 존재하게 됩니다.

그리고 데이터 셋에서 Output $y$를 임의로 만들어준 후에, Input $X$와 행렬곱을 했을 시 결과물의 부호가 Output $y$와 같은 Weight Vector $\mathbf{w}$를 찾아봅시다. 어렵게 찾을 필요 없이, 그냥 $X \mathbf{w} =y$가 성립하는 $\mathbf{w}$를 만들면 됩니다. 8번 슬라이드에서 행렬 $X$는 역행렬이 존재한다고 했으니, $\mathbf{w} = X^{-1}y$임을 쉽게 알 수 있습니다.

이 결과로 알 수 있는 것은 무엇일까요? 지금까지 전개한 내용은 $d$ 차원의 $d+1$개의 점을 배치했을 때 임의의 Output $y$에 대해서 $w$를 항상 구할 수 있다는 것이었습니다. 즉, 이 말은 $d+1$개의 점을 흩뿌릴 수 있다는 말과 동일하게 되니, $d_{VC}$는 최소한 $d+1$개 이상이다라는 말과 같습니다.

반대로 이제는 $d_{VC}$가 $d+1$ 이하라는 것을 보일 차례입니다. $d$는 차원을 의미하기 때문에 당연히 정수라는 것을 생각해본다면, 모든 $d+2$개의 점을 흩뿌릴 수 없다는 것을 보인다면 자연스레 $d_{VC}$가 $d+1$ 이하라는 것을 보일 수 있음을 알 수 있습니다.

그렇다면 이번에는 $d$ 차원인 $d+2$개의 임의의 점을 만들어봅시다. 여기서 알 수 있는 것은 차원의 수가 점의 수보다 적다는 겁니다. 따라서, 모든 점이 선형 독립인 것은 불가능합니다. 간단하게 생각해서 3차원의 점을 생각해본다면 선형 독립인 기저점은 $(1, 0, 0), (0, 1, 0), (0, 0, 1)$ 3개입니다. 만약에 여기서 그 어떤 점이 추가된다고 하더라도, 3개의 기저점을 적당히 조합한다면 만드는 것이 가능함이 자명합니다. 즉, $a \times (1, 0, 0) + b \times (0, 1, 0) + c \times (0, 0, 1) = $ 임의의 점이 성립한다는 것이고, 최소한 $a, b, c$ 중 하나는 0이 아니라는 겁니다. 마찬가지로 12번 슬라이드에서도 어떤 점 $x_j$을 다른 점들의 실수 배 $a_i$를 곱한 Vector를 더한다면 표현이 가능하다는 것이고, 최소한 그 $a_i$ 중 몇몇은 0이 아님을 보장할 수 있다는 것입니다.

이것이 의미하는 바는 상당히 큽니다. 만약 $x_j$ 중 0이 아닌 $a_i$를 생각해봅시다. $a_i$가 0이 아닌 점 $x_i$는 Output이 $y_i = sign(a_i)$와 같기 때문에 $x_j$의 Output $y_i$는 무조건 -1이 나올 수밖에 없습니다. 이 말은 +1/-1이 모두 가능하지 않다는 뜻이므로 $d+2$개의 점들을 흩뿌릴 수 없다는 이야기와 같습니다.

왜 그렇게 되는지를 자세히 한번 알아보겠습니다. 14번 슬라이드 맨 위에 나오는 식은 13번 슬라이드에 나왔던 식과 같습니다. 여기에 Weight Vector $\mathbf{w}$를 Transpose 시킨 다음 양 변에 똑같이 곱합니다. Output $y_{i}$의 정의에 의해, $sign(\mathbf{w}^{\sf T} \mathbf{x})$와 같습니다. 이전 페이지에서 $a_{i}$의 부호가 $y_{i}$의 부호와 같다고 했으니, $a_{i} \mathbf{w}^{\sf T} \mathbf{x}$는 무조건 0보다 클 수밖에 없습니다.

즉, $y_{j}$는 무조건 +1로 분류가 될 수밖에 없게 됩니다. 결론적으로, $d+2$개의 점은 흩뿌릴 수 없습니다.

지금까지의 과정을 통해 $d_{VC}$가 $d+1$ 이하라는 것과 $d_{VC}$가 $d+1$ 이상이라는 것을 모두 보였으므로 $d_{VC}$와 $d+1$이 같다는 것을 알 수 있습니다. $d+1$인 이유는 각각의 점이 $d$ 차원으로 이루어져 있는 것 + Threshold를 위한 0번째 원소의 존재라고 생각하시면 됩니다. 다시 말해, Input $X$를 통해 임의의 $y$ 값을 구할 수 있기 위해서는 Weight Vector $\mathbf{w}$가 $d+1$ 차원이면 됩니다.

Interpreting the VC dimension

이번에는 VC Dimension이 의미하는 바가 무엇인지를 알아보겠습니다.

첫째로, VC Dimension으로 모델의 자유도를 구할 수 있습니다. 물론, 매개변수의 개수도 자유도에 영향이 있습니다. 다만 자유도에 영향을 주는 방향이 서로 다릅니다. 쉬운 예시로 17번 슬라이드 오른쪽 그림과 같이 여러 개의 노브가 달려있는 오디오 시스템을 생각해봅시다. 최적의 음악을 듣기 위해서는 각각의 노브를 이리저리 돌려봐야 합니다. 매개변수는 각각의 매개변수에 대해 실수 Weight를 부여해야 합니다. 노브를 기준으로 생각해본다면, 어떤 노브를 얼만큼 돌려야 최적의 소리가 나오는지 찾는다고 생각해보시면 됩니다. VC Dimension을 노브에 빗대어 설명한다면, 이 노브를 돌릴 것인지 말 것인지를 결정한다고 보시면 됩니다. 똑같이 자유도를 판단하는 기준이지만, 이렇게 약간의 차이가 있음을 알게 되었습니다.

지금까지 여러번 보았던 예제들로 자유도를 구해봅시다. Positive Ray 예제는 $a$를 어디에 놓는가에 따라 데이터의 +1/-1 여부가 결정됩니다. 즉, 이 예제에서는 매개변수가 1개, VC Dimension도 1, 자유도도 1이 됩니다.

Positive Interval 예제도 마찬가지로, Interval을 확정하기 위해서는 두 개의 점을 정하는 것이 필요합니다. 즉, 매개변수는 2개가 되며 VC Dimension, 자유도도 마찬가지로 2 임을 알 수 있습니다.

이렇게 보면 자유도는 매개변수의 개수만 알면 구할 수 있지 않은가 하고 의문을 가지실 수도 있습니다. 매개변수의 갯수는 자유도에 영향을 주기는 하지만 그렇지 않은 경우도 있습니다. 가령 19번 슬라이드에 나온 것과 같이 1차원 Perceptron을 4개 연달아 배치한 예제를 살펴보겠습니다. 1차원 Perceptron이기 때문에 하나의 Perceptron에 사용되는 매개변수는 $w_0, w_1$로 2개입니다. 즉, 총 매개변수의 개수는 2+2+2+2=8개가 됩니다.

얼핏 보면 8개의 매개변수를 갖고 있기 때문에 8의 자유도를 가지고 있다고 착각할 수가 있습니다. 하지만 자세히 보시면 첫 번째 Perceptron을 거치는 순간 Output은 +1/-1 단 두가지 경우만 가능하게 됩니다. 즉, 두 번째 Perceptron의 Input도 +1/-1 단 두 가지 경우밖에 없다는 것입니다. 세 번째, 네 번째 Perceptron도 마찬가지입니다. 따라서 이 예제의 자유도는 2가 됩니다.

만약에 VC Dimension을 사용해 자유도를 찾게 된다면 매개변수의 갯수를 사용해 찾는 것보다 훨씬 간단하게 됩니다. 이 경우에는 1차원 Perceptron이므로 $d=1$입니다. VC Dimension은 차원 + 1이기 때문에 간단하게 $d_{VC}=2$임을 알 수 있습니다. VC Dimension과 자유도는 같으므로 자유도도 2 임을 바로 알 수 있습니다.

VC Dimension의 두 번째 의미는 VC Inequality를 만족하기 위해 필요한 데이터 수를 대략적으로 제공한다는 것입니다. VC Inequality도 Hoeffding’s Inequality와 마찬가지로, 의미있는 식이 되기 위해서는 오른쪽 항이 1보다 작아야 할 필요가 있습니다. 오른쪽 항을 작게 만들기 위해서 필요한 것은 충분한 크기의 $N$인데, 어느 정도의 값이 되어야 충분한지 한번 알아보겠습니다.

먼저 오른쪽 항이 조금 복잡한 형태이므로 간단하게 바꾸어 보겠습니다. 지난 장에서 Growth Function이 Dimension에 대해 Polynomial 하다는 것을 증명하였고, $e$ 지수에 달려있는 복잡한 식을 $N$만 남기고 모두 생략한다면, $N^{d}e^{-N}$ 으로 표현할 수 있습니다.

22번 슬라이드의 오른쪽 그림은 $d$의 크기를 5부터 30까지 5씩 늘려가며 그린 그래프입니다. 세로축의 단위 간격이 매우 커서 그래프가 살짝 이상하게 보이지만, 실제 그래프의 모양은 아래 그림과 같습니다.

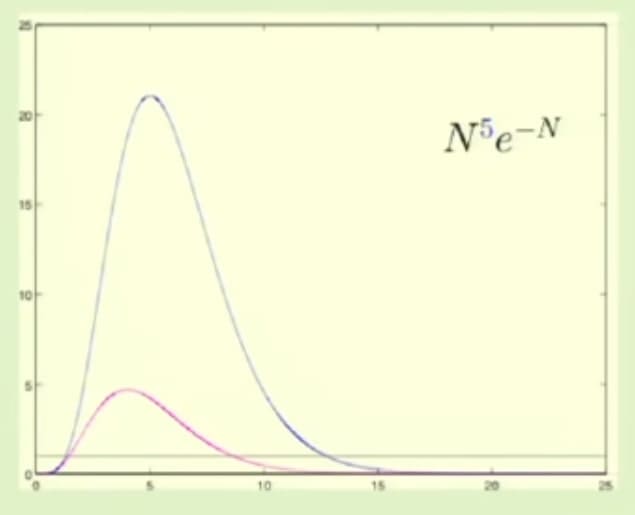
위 그래프에서 파란색 선이 $d=5$일 때의 그래프 모양입니다. $x$축 위에 있는 가로줄은 $y=1$을 의미합니다. 즉, 파란색 그래프가 $y=1$보다 작은 구역에 있어야만 VC Inequality에 의미가 생기게 됩니다. 그림상으로는 대략 13 정도로 보입니다.

이와 같은 방법으로 모든 $d$에 대해 적당한 $N$을 구해야 하는데, 일반적으로 정확하게 구하지 않고 Rule of Thumb (대략적인 값)을 구한다고 합니다. 이유는 데이터는 어차피 필요한 최소의 개수만 구하고 그만두지 않고 많으면 많을수록 좋기 때문이라고 생각합니다. 대략적으로 필요한 양은 VC Dimension의 10배 이상이라고 합니다.

여담으로 Rule of Thumb이란 이름이 붙은 이유는 측량 도구가 없던 옛날 시절, 길이를 재기 위해 엄지손가락을 많이 사용해서라고 합니다.

Generalization bounds

마지막으로 VC Dimension을 이용해 VC Inequality에 사용되는 변수들의 상한/하한점을 간단하게 구해보겠습니다.

20번 슬라이드에서도 다루었지만, 식을 조금 변형시키기 위해 VC Inequality의 오른쪽 항 전체를 $\delta$로 치환해 보겠습니다. 식을 $\epsilon$에 대해 정리하기 위해 $\epsilon$를 제외한 항들을 모두 $\delta$가 있는 항으로 이항시키면 23번 슬라이드의 두 번째 식이 나옵니다. $\epsilon$은 In Sample Error와 Out of Sample의 차이를 의미하기 때문에 이 값이 줄어들수록 좋은데, 그러기 위해서는 역시 $N$이 커야함을 알 수 있습니다.

$\epsilon$의 오른쪽 항을 $\Omega$ 함수로 정의한다면, 이 $\Omega$ 함수는 데이터의 수 $N$, 가설 $\mathcal{H}$, VC Inequality의 오른쪽 항 $\delta$에 영향을 받는 함수로 표현이 가능합니다.

추가로 VC Inequality 왼쪽 항의 확률은 Bad Event가 일어날 확률을 의미한다고 배웠습니다. 이를 Good Event로 바꾸게 되면 $1-\delta$의 확률로 In Sample Error와 Out of Sample의 차이가 $\Omega$ 이하라고 해석이 가능합니다.

23번 슬라이드 마지막에 유도한 식을 조금만 바꾸어 보겠습니다. 절댓값 부분을 없애고 싶은데, 일반적으로 Out of Sample Error가 In Sample Error보다 크므로 절댓값 부분을 없애게 되면 순서가 바뀌게 됩니다. 여기서 In Sample Error $E_{in}$을 오른쪽 항으로 이항 하게 되면 최종적으로 Out of Sample Error는 In Sample Error에 $\Omega$를 더한 값 이하라는 결론을 내릴 수 있습니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.