Error and Noise

4장에서는 Error와 Noise에 대해 알아보겠습니다.

Outline

이번 장의 구성은 총 4개로 나뉩니다.

먼저 지난 장 마지막에 다루었던 Nonlinear Transformation에 대해 좀 더 이야기해보고, 다음으로 Error를 측정하는 방법, 그리고 Noise가 발생하는 이유와 모델에 적용하는 법, 마지막으로 앞으로 이런 문제를 어떻게 접근할지에 대한 간단한 정리를 하며 마치게 됩니다.

Nonlinear transformation (continued)

지난 장에서 배웠던 Nonlinear Transformation의 과정을 한번 정리해봅시다. 이 문제가 시작된 이유는 주어진 데이터가 Linearly Seperable 데이터가 아니었기 때문에 우리가 배웠던 Linear Model을 직접적으로 적용할 수 없는 문제들이 존재했기 때문입니다. 그래서 이 문제를 어떻게 해결할지 고민하다가, Linear Model에서 Linear가 어디에 Linear 한 것이지를 생각해보았었죠. 여기서 Linear 하다는 것은 Input data $\mathbf{x}$에 Linear 한 것이 아니라 Weight Vector $\mathbf{w}$에 Linear 한 것이라고 배웠습니다. 이를 통해 Input data $\mathbf{x}$는 우리의 입맛에 맞게 Transform을 시켜도 문제가 없겠구나라는 결론에 도달한 것입니다. 따라서 기존의 Input data들이 $\mathcal{X}$라는 공간에 있다고 가정했을 때, 이들을 적절한 함수인 $\Phi$로 Transform 시켜서 Linearly Seperable 데이터가 되도록 만들어 줬습니다. 이때, Input data들을 $\Phi$로 Transform 시킨 공간을 $\mathcal{Z}$라 부르겠습니다.

이렇게 만든 새로운 공간인 $\mathcal{Z}$에서 기존에 우리가 알고있던 Linear Model을 적용해 문제를 해결했습니다. 예를 들면 PLA 같은 방법으로 말입니다. 그렇게 알고리즘을 수행 후 나온 결과는 $\mathcal{Z}$ 공간에서 정의된 Final Hypothesis $\tilde{g}$가 나오게 됩니다. (기존의 Input data가 존재하는 $\mathcal{X}$ 공간에서의 Final Hypothesis와의 차이를 두기 위해 $g$가 아니라 $\tilde{g}$라고 적은 겁니다. $\tilde{g}$는 ‘틸다 g’라고 읽습니다) 이때의 결과를 수식으로 표현하자면 $\tilde{g}(\mathbf{z})=\text{sign}(\tilde{\mathbf{w}}^{\sf T}\mathbf{z})$ 라고 쓸 수 있습니다. 하지만 우리가 원하는 결과는 $\tilde{g}$가 아니라 $g$ 입니다.

따라서 $\tilde{g}$를 초기에 했던 Transform $\Phi$의 역함수인 $\Phi^{-1}$로 Transform을 하게 되면 우리가 원하던 $g$가 나오게 됩니다. 단, $\mathcal{Z}$ 공간에서는 Linear Model로 $\tilde{g}$를 구하긴 했지만 원래의 $\mathcal{X}$ 공간에서 $g$는 Linear Model로 나오지 않습니다. (이해를 돕기 위해 $\Phi^{-1}$를 사용해서 $g$를 구하는 것처럼 설명했지만, 실제로는 이렇게 하지 않고 그냥 Input data $\mathbf{x}$를 $\Phi$로 Transform 해서 계산합니다. 왜 그런지는 다음 슬라이드에서 설명드리겠습니다.)

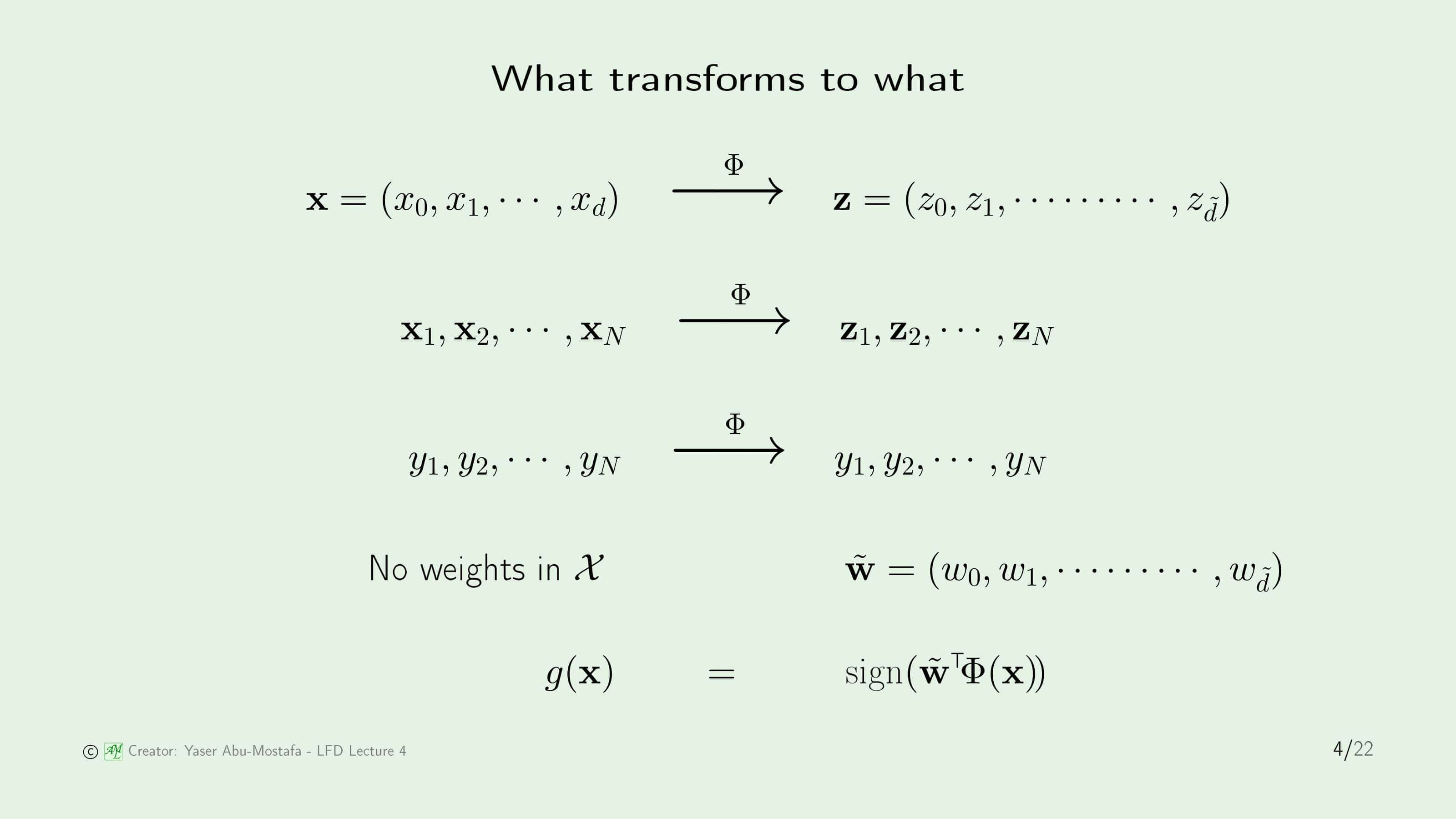
그렇다면 Transform $\Phi$를 통해서 과연 어떤 값들이 바뀌게 되는지 하나하나 따져보겠습니다.

먼저 Input data $\mathbf{x}$는 당연히 바뀌게 됩니다. $\mathbf{x}$가 바뀐다는 말은 Vector $\mathbf{x}$의 모든 값들이 $\Phi$를 거쳐 바뀌게 된다는 겁니다. (ex. $x_0 \to z_0$) 하지만 Output인 $y$는 바뀌지 않습니다. +1로 판단한 것은 그대로 +1, -1로 판단한 것은 그대로 -1로 남아야만 원래의 문제를 그대로 풀 수 있기 때문입니다. 이는 Regression에서도 마찬가지입니다.

Weight를 구하는 것이 목적이니 이것이 가장 중요한데, $\mathcal{X}$ 공간에서 직접적으로 Weight를 구하지 않기 때문에 $\mathcal{X}$ 공간에서의 Weight Vector는 존재하지 않습니다. Weight를 계산한 것은 $\mathcal{Z}$ 공간이니 $\tilde{\mathbf{w}}$ 만 존재합니다. 하지만 우리가 갖고있는 것은 $\mathbf{x}$이고 $g$를 이용해서 classification/regression을 사용해야 하니 $g(\mathbf{x})$를 아래와 같이 정의합니다.

\[g(\mathbf{x}) = \text{sign}(\tilde{\mathbf{w}}^{\sf T}\mathbf{z}) = \text{sign}(\tilde{\mathbf{w}}^{\sf T}\Phi(\mathbf{x}))\]

여기서 아니 그냥 $\tilde{\mathbf{w}}$에 $\Phi^{-1}$를 취해서 $\mathbf{w}$를 구하면 되는거 아닌가? 왜 이렇게 불편하게 $g$를 계산하지? 라는 의문을 가질 수도 있습니다. 물론 그 방법이 더 간단합니다만, $\Phi^{-1}$가 존재하지 않을 수 있다는 것이 문제입니다. 예를 들어 만약에 Transform $\Phi$를 통해서 차원이 늘어난다면, 하나의 $\mathcal{Z}$ 공간의 좌표인 $\mathbf{z}$에서 여러 개의 $\mathbf{x}$와 대응할 수 있는 문제가 발생합니다. 따라서 조금 불편하더라도 $g$를 계산할 때 Input data를 $\Phi$로 Transform 할 수밖에 없는 것입니다.

Error measures

다음으로 Error Measure에 대해 알아보겠습니다.

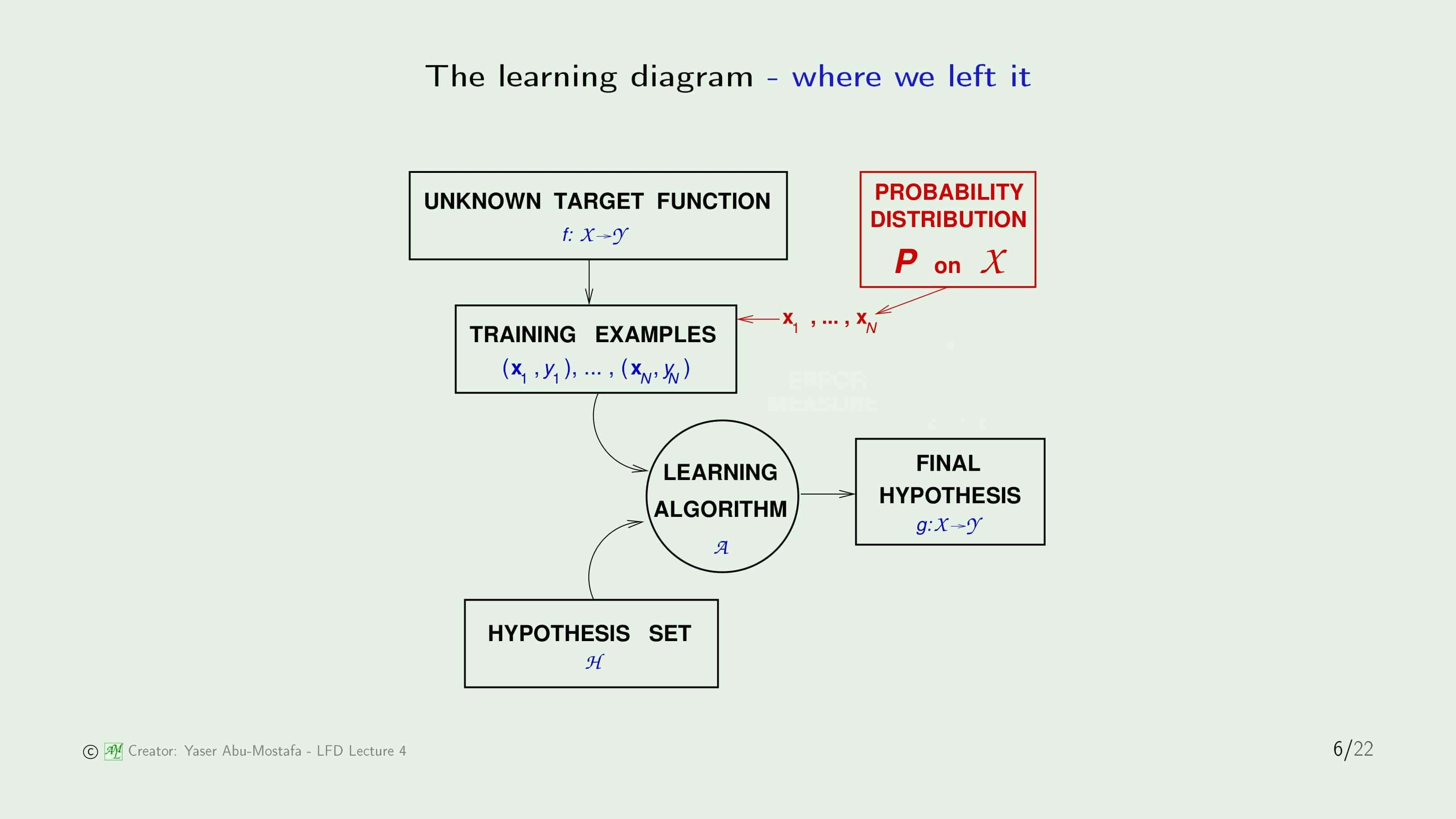
Error Measure를 하기 전에 기존에 배웠던 Learning Diagram을 다시 살펴봅시다. 간단하게만 다시 설명드리면, Input Data $\mathbf{x}$는 어떤 확률 분포에 의해 생성되고, Target Function $f$에 의해 $y$값이 결정되어 Training Example $(\mathbf{x}_i, y_i)$가 생성된다고 가정합니다. 그 후 여러 개의 Hypothesis Set (ex. Perceptron)을 통해 Learning Algorithm (ex. PLA)을 거쳐 $f$와 가장 가까운 Final Hypothesis $g$를 얻는 것입니다.

그렇다면 $h$와 $f$가 가깝다($h \approx f$)는 어떻게 정의해야 할까요?

이를 정량적으로 측정하기 위해 Error Measure $E(h, f)$를 정의합니다. 다만 직접적으로 두 함수 $h$와 $f$를 구할 수가 없기 때문에, Input data $\mathbf{x}$를 넣었을 때의 값의 차이로 정의하게 됩니다. 이 때, $\mathbf{x}$는 함수 $h$, $f$의 한 점으로 볼 수 있기 때문에 이를 Pointwise로 정의한다고 부릅니다.

그런데, 우리는 이미 Error Measure 방법 중 두 가지를 배웠습니다. Linear Regression에서는 $h$와 $f$의 함수값의 차이의 제곱으로 정의한 Squared Error로 정의했고, Linear Classification에서는 맞았는가/틀렸는가를 비교했기 때문에 Binary Error를 사용하였습니다.

점 $\mathbf{x}$에서 각각 에러를 계산하는 것은 이렇게 간단합니다. 하지만 우리가 원하는 것은 각각 점에서의 에러가 아니라, $h$의 전체적인 에러입니다. 즉, 함수 $h$가 함수 $f$와 얼마나 다른가를 알고싶다는 것입니다.

가장 간단한 방법으로 Error의 평균값을 사용합니다. In Sample Error와 Out of Sample Error 모두 평균값을 사용합니다. 그런데 In Sample Error는 우리가 갖고있는 데이터를 사용해서 구하면 되지만, Out of Sample Error는 어떻게 구해야 하는지에 대한 의문이 생깁니다. 이 방법은 다음 장에서 다루도록 하고, 우선은 전체적인 Error는 Sample의 평균 Error를 사용한다는 것만 짚고 넘어갑시다.

Learning Diagram에서 Error를 포함한 그림입니다. Error를 측정할 때 각각 $\mathbf{x}$ 점에서의 $h$와 $f$의 함수값의 차이의 평균으로 계산한다고 말씀드렸습니다. 여기서 $\mathbf{x}$는 특정한 확률 분포로부터 생성된 점이기 때문에 위의 그림과 같이 표현됨을 알 수 있습니다. Final Hypothesis $g$는 이 Error의 평균값이 가장 낮은 Hypothesis로 결정됩니다.

그럼 이 Error Measure를 어떻게 결정해야 하는지도 중요합니다. 기존의 Error Measure 방법은 Squared Error와 Binary Error를 다루었습니다만, 이 둘은 일부일 뿐 모든 상황에 적용할 수 있는 방법이 아닙니다.

예를 들어, 기계학습으로 지문을 인식하는 프로그램을 구현했다고 가정해봅시다. 기계학습은 완벽하지 못하기 때문에, 아무리 완벽에 가깝게 구현했다고 할지라도 Error가 발생할 수 있습니다. 이 경우 발생할 수 있는 에러는 2가지입니다. False Accept Error는 등록되지 않은 지문을 정상으로 판단하는 오류이고, False Reject Error는 정상으로 등록된 지문을 침입자로 판단하는 오류입니다.

그렇다면 각각의 상황에서 어느정도의 페널티를 주는 것이 적당할까요? 이 문제는 Classification이기 때문에 그냥 Binary Error를 사용하면 된다고 생각하실 수도 있습니다만, 다음 두 가지 예시를 통해 그렇게 간단한 문제가 아님을 알 수 있습니다.

이 지문 인식 프로그램이 마트에 설치되어 있다고 가정해봅시다. 마트에서는 지문이 등록된 회원들에게 할인해주는 이벤트를 하고 있습니다. 이 상황에서 발생할 수 있는 두 가지 Error에 대해 어떻게 페널티를 주어야 하는지 생각해봅시다.

만약 마트의 회원이 할인 이벤트로 인해 마트에 갔는데 False Reject가 발생하여 컴퓨터가 지문을 제대로 인식 못해 몇번이나 손을 갖다대야 하는 상황이 온다면 그 고객은 몹시 기분이 나쁠 것입니다. 최악의 경우에는 단골 고객을 잃을 수도 있습니다. 다만 반대로, 우연히 지나가다 마트에 들른 비회원이 심심해서 지문을 갖다댔는데 컴퓨터가 회원으로 인식해서 할인을 해주는 상황(False Accept)은 마트 입장에서 크게 문제가 아닙니다. 마트는 그냥 약간의 금전적인 손해만 보고, 새로운 고객을 유치할 기회를 얻을 수도 있습니다. 이런 상황에서는 False Reject에 큰 패널티를 부여하고, False Accept는 그보다 낮은 페널티를 부여하는 것이 적절할 것입니다. 하지만 다른 상황에서도 마찬가지일까요?

이번에는 이 지문 인식 프로그램이 국가정보원에 설치되어 있다고 가정해봅시다. 국가정보원의 1급 비밀이 담긴 금고는 요원들의 지문을 통해서만 열립니다. 만약 여기서 False Accept가 발생한다면 엄청난 문제가 발생할 수 있음을 알 수 있습니다. 최악의 경우에는 간첩의 지문만으로 금고가 열려서 국가 기밀이 노출되는 상황이 발생하겠죠.

하지만 False Reject는 그다지 큰 문제가 아닙니다. 요원의 경우 이게 직업이고, 컴퓨터가 몇번 인식 못한다고 해도 툴툴대며 다시 손가락을 갖다댈 것이니까요. 따라서 이 경우에는 False Accept에 큰 패널티를 부여하고, False Reject는 그보다 낮은 페널티를 부여하는 것이 적절할 것입니다.

이 두 가지 상황을 통해, 같은 문제라도 상황에 따라 다른 Error Measure를 적용해야 함을 알 수 있습니다. 그런데 만약에 이렇게 구체적인 Error Measure를 사용할 수 없을 때는 어떻게 해야 할까요?

크게 두 가지가 있습니다. Plausible Measure는 Error가 특정한 분포를 따를 것이다 라고 가정하는 것입니다. 가령 어떤 문제에서 Error가 가우시안 분포를 따른다라고 가정하는 것이죠. Friendly Measure는 수학적인 방법으로 Error를 계산하는 방법입니다. Closed-form을 통해 답을 구하거나, Convex Optimization을 통해 답을 구하는 방법입니다.

온라인 강의에서도 이 방법들에 대해서는 그냥 이렇게만 설명만 하고 지나갔었기 때문에, 그냥 이러이러한 것이 있구나라고만 알고 넘어가시면 될 것 같습니다.

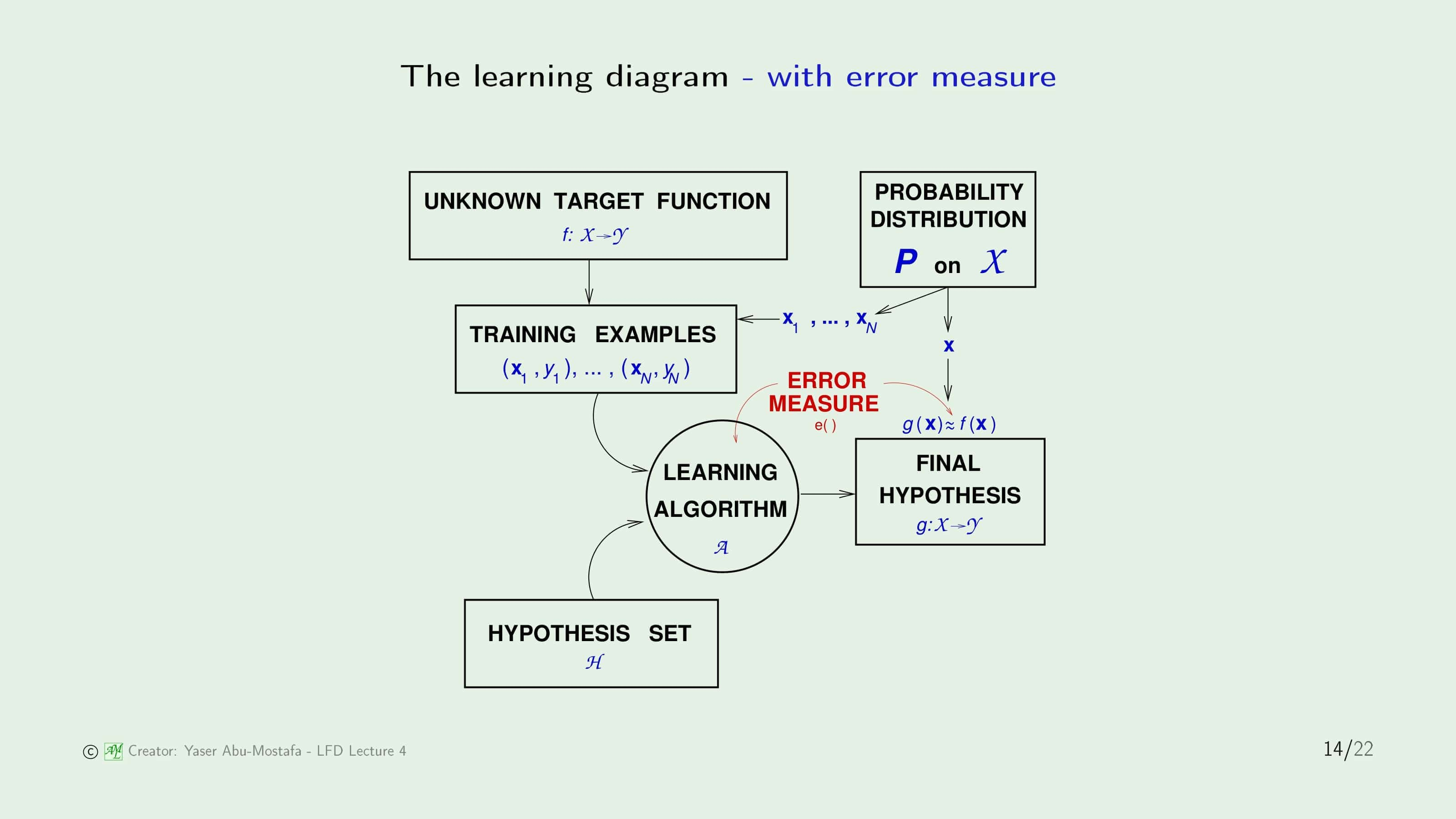
방금 배운 Error Measure를 Learning Diagram에 적용한 그림입니다. Learning Algorithm에서 Error Measure를 통해 Fianl Hypothesis를 도출한다는 것을 표현한 것이 추가된 그림입니다.

Noisy targets

이제 Noise Target이라는 것이 무엇인지 알아보겠습니다.

지금까지 우리가 구해야하는 목표를 Target Function이라고 표현했지만, 사실 이 Target Function은 Function이 아닐 수도 있습니다. (Function이 아니라는 것은 하나의 데이터에 대해서 여러 가지 값이 나올 수도 있다는 말입니다.)

지난번에 사용했던 카드 발급 문제를 예를 들면, 이 카드 회사에는 지금까지 고객의 정보를 기반으로 카드를 방급해 주었는지/거절했는지를 판단한 데이터가 있습니다. 이 데이터중에서는 우연히 고객의 정보가 동일한 케이스도 있을 것입니다. 그런데 카드 발급 여부를 결정한 사람이 다르다던가, 같은 사람이라도 그날의 기분이 좋고/나쁘고의 이유로 인해 한명에게는 카드를 발급해주고, 다른 한명에게는 거절한 경우가 있을 수 있습니다.

그래서 이제는 Target Function 이라는 표현 대신에 Target Distribution 이라고 표현할 것입니다. 즉, $y=f(\mathbf{x})$ 라는 표현 대신에 $P(y \mid \mathbf{x})$라는 표현을 쓰겠다는 얘기입니다. $P(y \mid \mathbf{x})$는 Input Data가 $\mathbf{x}$일 때 $y$라는 결과가 나올 확률을 의미합니다. 그런데 Input Data $\mathbf{x}$도 어떤 확률 분포에 의해 생성된다고 했으니 (Learning Diagram 참고) Input data $\mathbf{x}$가 생성될 확률을 $P(\mathbf{x})$라 할 수 있습니다. 따라서 종합적으로 $(\mathbf{x}, y)$라는 데이터가 생성될 확률은 $P(\mathbf{x})P(y \mid \mathbf{x})$ 라고 볼 수 있습니다.

이를 토대로 Noisy Target를 정의해 보면 Deterministic Target $f(\mathbf{x})$를 평균적인 값 $\mathbb{E}(y \mid \mathbf{x})$로 정의했을 때 Output $y$와 $f(\mathbf{x})$의 차이라고 볼 수 있습니다. Deterministic Target이란 Noise가 하나도 없는 Target이라는 뜻입니다. (즉, 우리가 원래 알고있던 Target Function과 동일합니다)

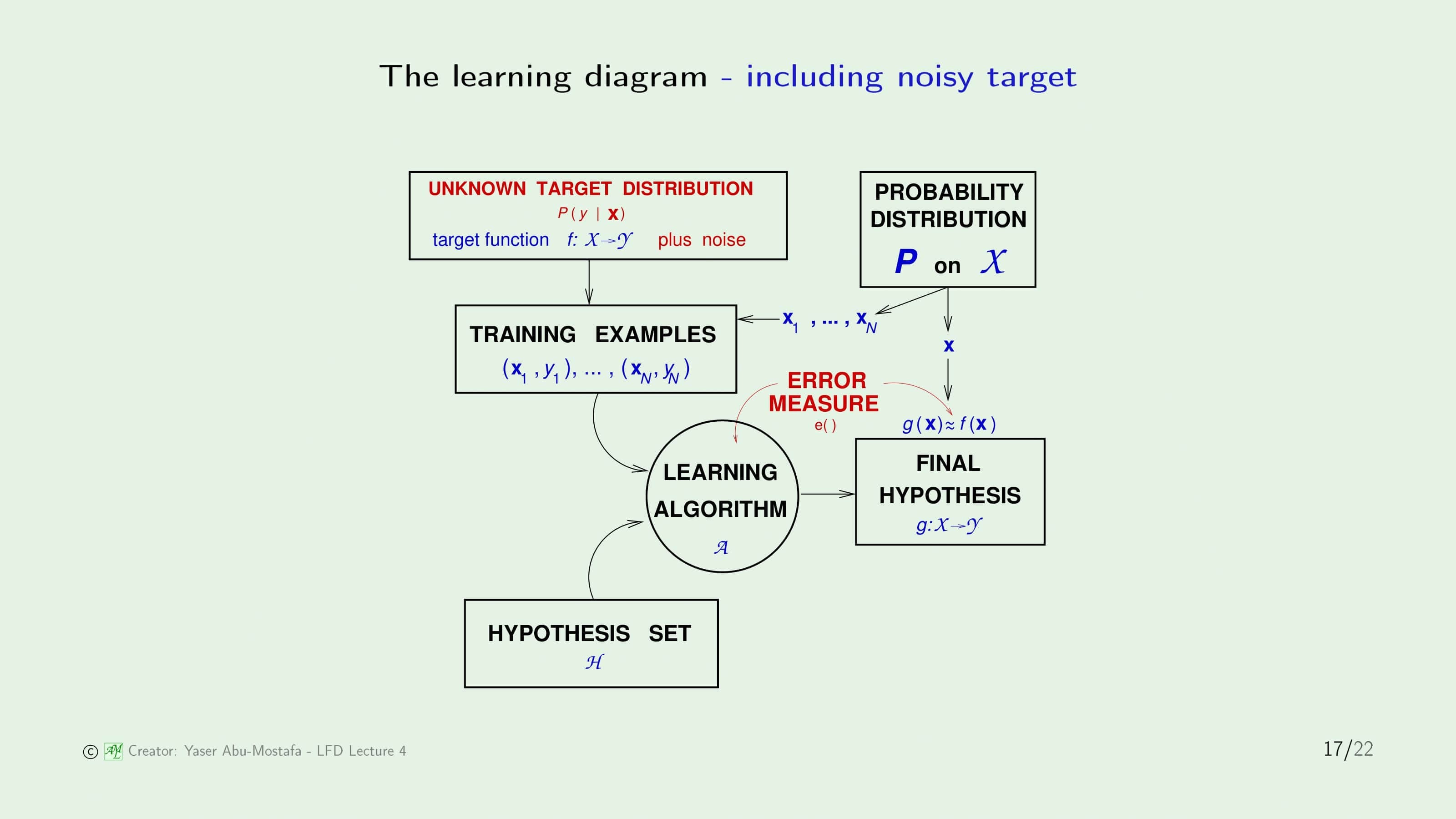
이 Noise를 반영한 Learning Diagram입니다. 자꾸 아까부터 Learning Diagram에 하나씩 추가되어 짜증나실 수도 있는데 다행이 이 그림이 최종판입니다. 왼쪽 위의 Target Function이 Target Distribution으로 바뀌었습니다. Target Distirubution이라는 것은 Target Function에 Noise를 추가한 것으로 보시면 됩니다.

이번엔 $P(y \mid \mathbf{x})$와 $P(\mathbf{x})$의 차이를 알아보겠습니다.

$P(y \mid \mathbf{x})$는 데이터 $\mathbf{x}$가 들어왔을 때 Output $y$가 나올 확률입니다. 실질적으로 우리가 학습하고 싶은 값이 됩니다. $P(\mathbf{x})$는 데이터 $\mathbf{x}$가 얼마나 자주 등장하는지를 나타냅니다. 특정한 데이터가 너무 자주 나오게 되면 학습 모델이 잘못될 수 있기 때문에 겉으로는 드러나지 않아도 이 값도 무시할 수는 없습니다. 이전 슬라이드에서 $(\mathbf{x}, y)$는 $P(\mathbf{x})P(y \mid \mathbf{x})$로 계산되었으니 이 두 가지 컨셉이 합쳐있음을 알 수 있습니다.

Preamble to the theory

마지막으로 이를 통해 앞으로 어떻게 접근할 것인지 간단하게 정리하고 마치겠습니다.

2장에서 학습이 가능한가를 따졌을 때 In Sample Error와 Out of Sample Error를 최대한 비슷하게 만드는 것이 좋다고 하였습니다. 그런데 이걸 Learning이라고 말할 수 있을까요? 사실 Learning이라는건 Out of Sample Error를 0에 가깝게 만드는건데, 이 두 표현이 같다고 볼 수는 없습니다. 극단적인 예시로 In Sample Error와 Out of Sample Error가 둘다 1이라고 해도 어쨌든 같아지기 때문입니다.

그럼 지금까지 배운 내용을 토대로 Out of Sample Error를 0에 가깝에 유도할 수 있는 방법이 무엇인지 살펴보겠습니다.

2장에서 In Sample Error와 Out of Sample Error를 최대한 비슷하게 만들어야 한다고 언급했었고, 3장에서 In Sample Error를 0에 가깝게 만들어야 한다고 했습니다. 그렇다면 $0 \approx E_{in} \approx E_{out}$로 합치게 되면 Out of Sample Error를 0에 가깝게 유도할 수 있음을 알 수 있습니다. 따라서 다음 장에서는 이 2가지를 각각 따로 다루게 될 예정입니다. $E_{out} \approx E_{in}$을 구하는 방법은 2개 장에 걸쳐 다룰 예정이고, $E_{in} \approx 0$은 4개 장에 걸쳐 다룰 예정입니다.

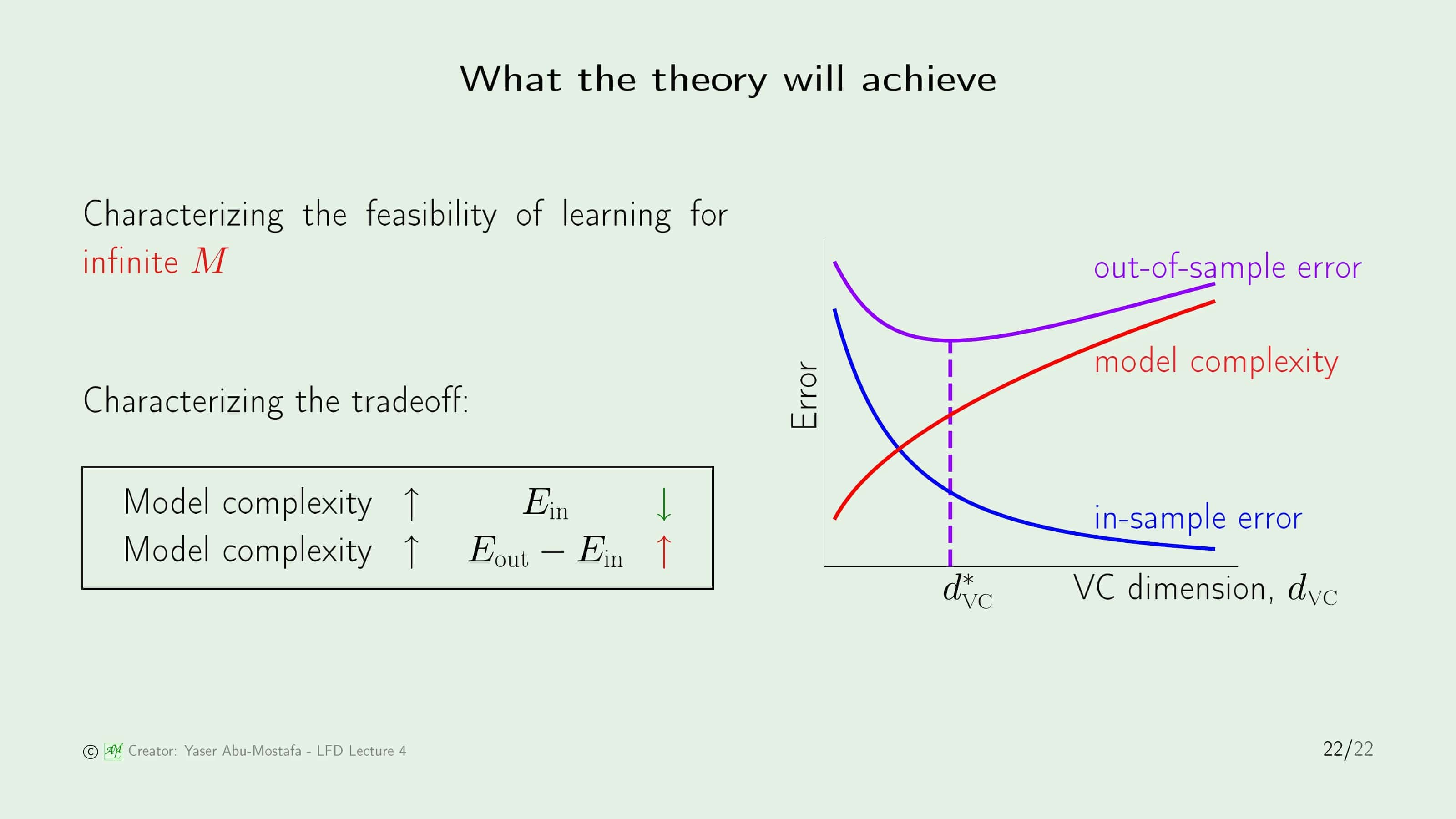
전체적인 그림은 위 슬라이드의 오른쪽 그림과 같습니다. In Sample Error가 0으로 다가갈수록 Out of Sample Error도 작아진다면 이상적이겠지만, 안타깝게도 In Sample Error를 어느정도까지 낮출 때는 Out of Sample Error도 낮아지지만, In Sample Error를 과도하게 0에 가깝게 맞추게 된다면 오히려 Out of sample Error가 커지는 문제가 있습니다. 왜냐하면 In Sample Error는 낮추려면 Model Complexity가 점점 높아지는데 이것은 Out of Sample Error를 높이기 때문입니다. (이것은 9장 Overfitting에서 더 자세히 다룰 예정입니다)

따라서 Trading off를 정리해보면, Model Complexity가 높아질수록 In Sample Error가 낮아지지만, Out of Sample Error와 In Sample Error의 차이는 늘어난다는 관계가 있습니다. 그러므로 이를 적당히 조절할 수 있는 점을 찾는 것이 중요한데, 이는 VC Dimension이라는 것으로 계산할 수 있습니다. VC Dimension은 6장에서 다룰 예정입니다.

이번 장은 여기까지입니다. 감사합니다.