Kernel Methods

15장은 Kernel Method를 배우게 됩니다. 지난 시간에 배웠던 Support Vector Machine에서 이어지는 내용입니다.

Outline

이번 장은 크게 두 주제로 나뉘어 있습니다. 비선형 변환을 처리하기 위한 Kernel Trick이 무엇인지를 먼저 배우고, SVM의 방법 중 하나인 Soft-margin SVM을 배우게 됩니다. 두 주제가 서로 연관이 되어있지는 않지만, 두 주제 모두 비선형 문제를 해결하기 위한 시도라고 생각하시면 됩니다.

The Kernel trick

지금까지 비선형 문제를 풀기 위해서는 비선형 문제를 선형 문제로 변환시키기 위해 $\mathcal{Z}$ 공간으로 데이터를 Transform 시키는 방법을 사용하였습니다. 그러나 일반적으로 적당한 Transform Function $\Phi$를 찾는 것은 쉽지 않기 때문에 Transform을 시키지 않은 채로 비선형 문제를 해결하는 방법이 필요합니다. Kernel의 아이디어는 바로 거기서부터 시작합니다.

먼저 지금까지 $\mathcal{Z}$ 공간에서 어떤 일을 했었는지를 떠올려봅시다. 지난 시간에 배웠던 라그랑지안 $\mathcal{L}$ 식에서 맨 뒷부분을 보시면, 보라색으로 표시된 $\mathbf{z}^{\sf T}_{n}$과 $\mathbf{z}_m$의 내적 부분이 바로 유일하게 $\mathcal{Z}$ 공간이 사용되는 부분입니다. 라그랑지안에서의 Constraints 부분은 $\mathcal{Z}$ 공간과 관련이 없습니다.

라그랑지안을 풀고 찾은 가설 $g$에도 $\mathbf{z}$가 쓰입니다. 그런데 $g$에서의 Weight인 $\mathbf{z}$가 쓰이므로, 결과적으로 가설 $g$에는 $\mathbf{z}$ 자체보다는 $\mathbf{z}_n$과 $\mathbf{z}$의 내적만이 필요합니다. $b$ 또한 식을 살펴보면 $\mathbf{z}_n$과 $\mathbf{z}_m$의 내적만 알고 있다면 구할 수 있습니다.

이로써 알 수 있는 것은 라그랑지안을 통해 $\mathcal{Z}$ 공간에서 가설 $g$를 구하기 위해서는 $\mathbf{z}$를 직접 구할 필요 없이 $\mathbf{z}$ 간의 내적만 알 수 있으면 된다는 것입니다. 만약에 $\mathcal{Z}$ 공간까지 가지 않더라도 $\mathbf{z}$ 간의 내적을 구할 수 있다면, 굳이 힘들게 데이터들을 $\mathcal{Z}$ 공간으로 Transform 시키는 수고를 하지 않아도 될 것입니다.

주어진 데이터는 $\mathcal{X}$ 공간에 있는 임의의 두 점 $\mathbf{x}$와 $\mathbf{x}’$이라고 가정합시다. 이 두 점을 $\mathcal{Z}$ 공간으로 Transform 시킨 점을 $\mathbf{z}$와 $\mathbf{z}’$이라고 하면, 우리가 원하는 것은 주어진 데이터만으로 $\mathbf{z}$와 $\mathbf{z}’$의 내적을 구하는 것입니다. 이 내적을 $K(\mathbf{x}, \mathbf{x}’)$으로 표현하고, Kernel이라고 부릅니다.

이해를 돕기 위해 주어진 데이터가 $\mathbf{x} = (x_1, x_2)$라고 가정해 보겠습니다. 만약 Transform Function $\Phi$이 2차 다항식으로 주어진다면 Transform을 한 결과는 $\mathbf{z} = (1, x_1, x_2, x_1^2, x_2^2, x_1 x_2)$가 됩니다. $K(\mathbf{x}, \mathbf{x}’)$를 계산하는 과정은 아래와 같습니다.

\[\begin{align} K(\mathbf{x}, \mathbf{x}') &= \mathbf{z}^{\sf T} \mathbf{z}' \\&=(1, x_1, x_2, x_1^2, x_2^2, x_1 x_2) \cdot (1, {x'}_1, {x'}_2, {x'}_1^2, {x'}_2^2, {x'}_1 {x'}_2) \\&=1 + x_1 {x'}_1 + x_2 {x'}_2 + x_1^2 {x'}_1^2 + x_2^2 {x'}_2^2 + x_1 {x'}_1 x_2 {x'}_2 \end{align}\]

그렇다면 두 점 $\mathbf{x}$와 $\mathbf{x}’$을 Transform을 하지 않고 $K(\mathbf{x}, \mathbf{x}’)$를 구하는 방법을 알아보겠습니다.

이번에는 Kernel Function을 $K(\mathbf{x}, \mathbf{x}’) = (1 + \mathbf{x}^{\sf T} \mathbf{x}’)^2$로 가정해봅시다. 이 식을 전개하면 $1 + x_1^2 {x’}_1^2 + x_2^2 {x’}_2^2 + 2 x_1 {x’}_1 + 2 x_2 {x’}_2 + 2 x_1 {x’}_1 x_2 {x’}_2$가 되는데, 잘 살펴보면 두 벡터 $(1, x_1^2, x_2^2, \sqrt{2} x_1, \sqrt{2} x_2, \sqrt{2} x_1 x_2)$와 $(1, {x’}_1^2, {x’}_2^2, \sqrt{2} {x’}_1, \sqrt{2} {x’}_2, \sqrt{2} {x’}_1 {x’}_2)$의 내적을 수행한 결과라는 것을 알 수 있습니다.

이렇게 $(1 + \mathbf{x}^{\sf T} \mathbf{x}’)$의 제곱의 형태인 Kernel을 Polynomial Kernel (다항식 커널)이라고 부릅니다.

일반적인 상황을 고려하기 위해 $d$차원의 주어진 데이터를 $Q$차 다항식으로 Transform을 하게 된다면, 이와 동등한 Kernel은 $K(\mathbf{x}, \mathbf{x}’) = (1 + \mathbf{x}^{\sf T} \mathbf{x}’)^Q$로 표현할 수 있습니다.

그런데 문제는 만약 $d$와 $Q$가 커지게 되면 $K(\mathbf{x}, \mathbf{x}’)$를 구하기가 너무 어렵다는 것입니다. 슬라이드에 나온대로 $d=10$, $Q=100$인 상황만 가정하더라도 10차 다항식을 100제곱 하는 결과를 구해야 하는데, 계산량이 너무 많아 전개하는 것이 거의 불가능합니다.

그렇기 때문에 Polynomial Kernel에서는 $\mathbf{x}^{\sf T} \mathbf{x}’$를 전개하지 않고 $a \mathbf{x}^{\sf T} \mathbf{x}’ + b$ 의 형태로 만들어 이항정리를 사용해 $\mathbf{x}^{\sf T} \mathbf{x}’$의 계수만을 구하게 됩니다.

Kernel이 두 점 $\mathbf{x}$와 $\mathbf{x}’$의 내적으로 정의된 문제는 해결되었으나, 그 외에 상황을 고려할 필요가 있습니다. 이번 예제에 나온 Kernel은 $\mathbf{x}$와 $\mathbf{x}’$의 내적으로 표현되지 않고 Euclidean Norm으로 표현되고 있습니다. 이런 식의 Kernel이 $\mathcal{Z}$ 공간에 존재하는 지를 보여야 합니다.

결론부터 말하면 이 Kernel은 무한차원의 $\mathcal{Z}$ 공간에 존재합니다. 간단한 예를 들면 주어진 점 $\mathbf{x}$를 1차원이라 가정합니다. 그렇다면 $\mathbf{x}$와 $\mathbf{x}’$는 모두 스칼라로 표현이 되므로 $x$와 $x’$으로 대체합니다. 그리고 $\gamma$를 간단하게 1로 놓습니다.

그런 후에 이 식을 Taylor Series (테일러 급수)로 표현한다면 좀 더 복잡한 식이 되긴 합니다. 하지만 보기 쉽게 $x$와 $x’$를 갖고 있는 것을 각각 분리한다면 두 무한 차원의 벡터의 내적으로 이루어진 식임을 알 수 있습니다.

참고로 이런 Kernel을 Radial Basis Function Kernel이라고 합니다. 다음 장에서 이를 더 자세하게 다룰 예정입니다.

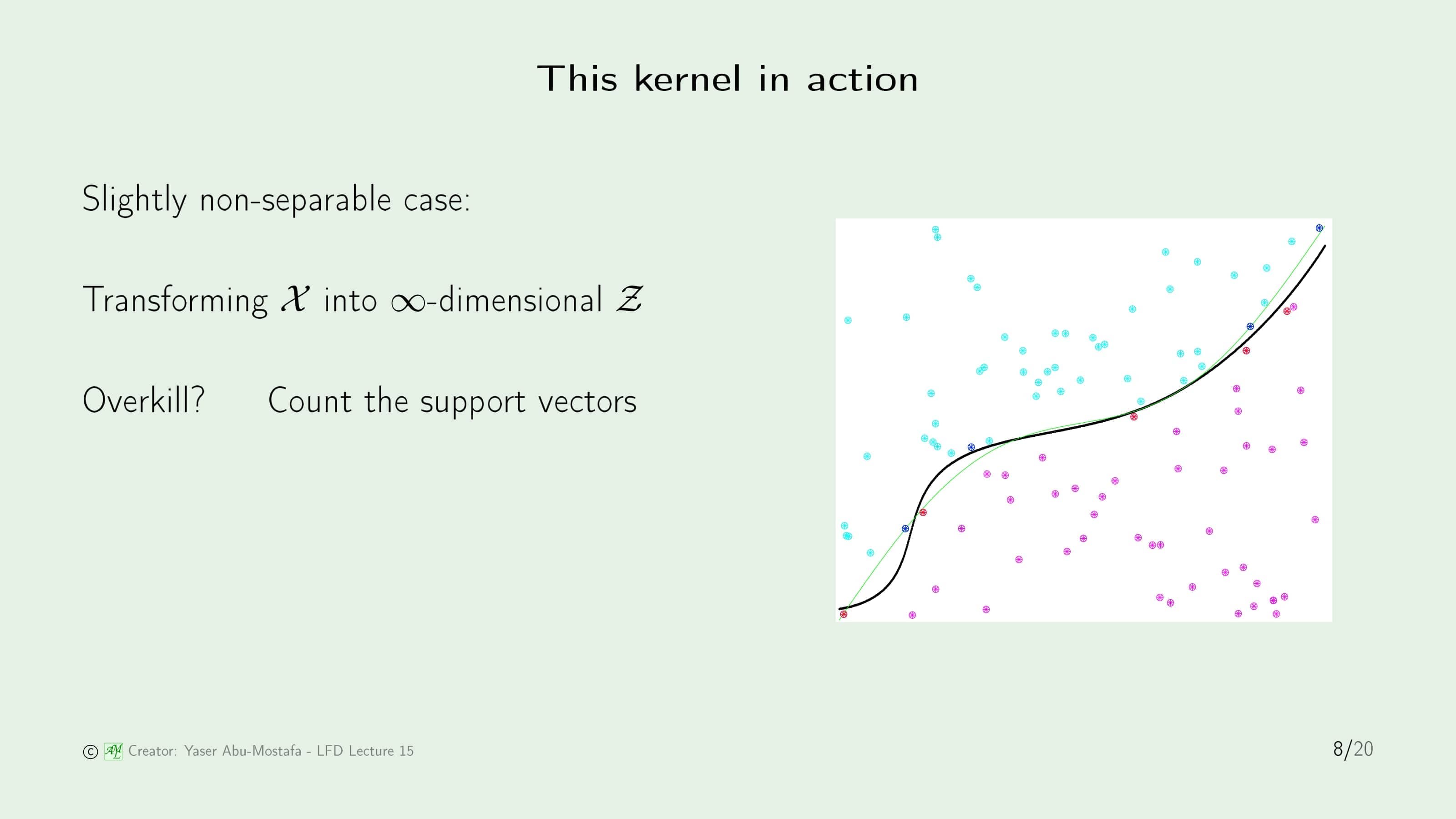
이제 Kernel을 실제 비선형 문제에서 적용하는 방법을 살펴봅시다. 주어진 $\mathcal{X}$ 공간의 데이터들을 무한 차원인 $\mathcal{Z}$ 공간에 Transform 할 필요 없이, 이전 슬라이드에서 배운 Kernel만을 사용할 것입니다. Kernel을 Quadratic Programming에 입력하면 알아서 Support Vector가 구해지기 때문에 직접적인 계산은 필요가 없습니다.

그림이 작아서 잘 보이진 않지만, 파란색의 점과 빨간색의 점이 양쪽의 Support Vector입니다. 그리고 그 Support Vector를 따라 그린 검은색 곡선이 학습 결과가 됩니다. Support Vector인데 왜 Margin이 크지 않는지 궁금해하실 수도 있는데, 이 검은색 곡선은 $\mathcal{Z}$ 공간에서 Margin이 최대인 직선으로 그린 것이기 때문에 지금 보는 $\mathcal{X}$ 공간과는 관련이 없습니다.

Support Vector Machine을 계산할 때, 위와 비슷한 Quadratic Programming 문제를 풀었던 것을 기억하실 겁니다. 그 당시에는 $\mathcal{X}$ 공간의 문제를 풀었기 때문에 저 자리에 $\mathbf{x}$와 $\mathbf{x}’$의 내적이 들어가 있었습니다. 비선형 문제를 풀기 위해서는 저 자리에 $\mathbf{z}$와 $\mathbf{z}’$의 내적이 있어야 하지만, 그것이 싫어 $K(\mathbf{x}, \mathbf{x}’)$로 대체한 것이 지금까지 한 내용입니다.

이제 Kernel에서 Final Hypothesis를 어떻게 구하는지를 알아봅시다.

이전에도 보았듯이, Hypothesis를 $\mathcal{Z}$ 공간에서 구했기 때문에 $g$는 $\mathbf{z}$가 포함된 식으로 표현이 가능했습니다. 하지만 지금까지 우리는 $\mathbf{z}$를 배제해왔으니, 이것 대신 Kernel $K( - , - )$로 표현할 수 있도록 식을 바꾸어봅시다.

이번 장의 앞부분에서 했던 것처럼 $\mathbf{w}$를 풀어서 전개하면 $\mathbf{z}$ 간의 내적으로 표현할 수 있게 되고, 그 부분을 $K(\mathbf{x}_n, \mathbf{x})$로 대체할 수 있습니다. 시그마가 포함된 앞부분은 더이상 정리할 수 없지만, $b$는 또다시 Kernel로 표현할 수 있습니다.

지금까지 배운 Kernel의 유일한 문제, 스스로 만든 임의의 Kernel이 유효한지를 알 수 없다는 것입니다. 다시 말해, 우리가 제시한 Kernel이 어떤 $\mathcal{Z}$ 공간에서 나온 Kernel임을 보여야 한다는 것입니다.

크게 3가지 접근방법이 있는데, 첫 번째는 Polynomial Kernel과 같이 개념적인 방법으로 접근하여 Kernel을 만드는 방법입니다. 두 번째는 다음 슬라이드에서 설명할 Kernel의 수학적인 특성을 이용하는 것입니다. 세 번째는 저자분이 선호하는 방법이라고 하는데 그냥 신경 쓰지 않는 방법이라고 합니다.

이전 슬라이드에서 말한 Kernel의 수학적인 특성을 이용해 Kernel을 디자인해봅시다. 임의의 Kernel이 유효하기 위한 필요충분조건은 첫째로 Symmetric 해야 한다는 조건이 있습니다. 이것은 $\mathbf{x}$와 $\mathbf{x}’$의 위치를 서로 바꿔도 원래의 식과 동일해야 한다는 것입니다.

두번째는 모든 데이터 점을 사용해 만든 Kernel Matrix가 Positive Semi-Definite여야 합니다. Matrix가 Positive Semi-Definite라는 것은 해당 Matrix의 모든 Eigenvalue가 음수가 아니라는 것인데, 일반적으로는 영벡터가 아닌 $x$에 대해 $x^{\sf T} M x \ge 0$이라면 Matrix $M$이 Positive Semi-Definite라고 부릅니다.

이 수학적 특성을 Mercer’s Condition이라고 부르는데, 보시다시피 두 번째 조건은 데이터의 많은 경우 계산이 어렵기 때문에 실제로 이를 보이는 것은 쉽지 않습니다.

Soft-margin SVM

Kernel에 대한 이야기는 끝났고, 다음으로는 Soft-margin SVM에 대해 알아봅시다.

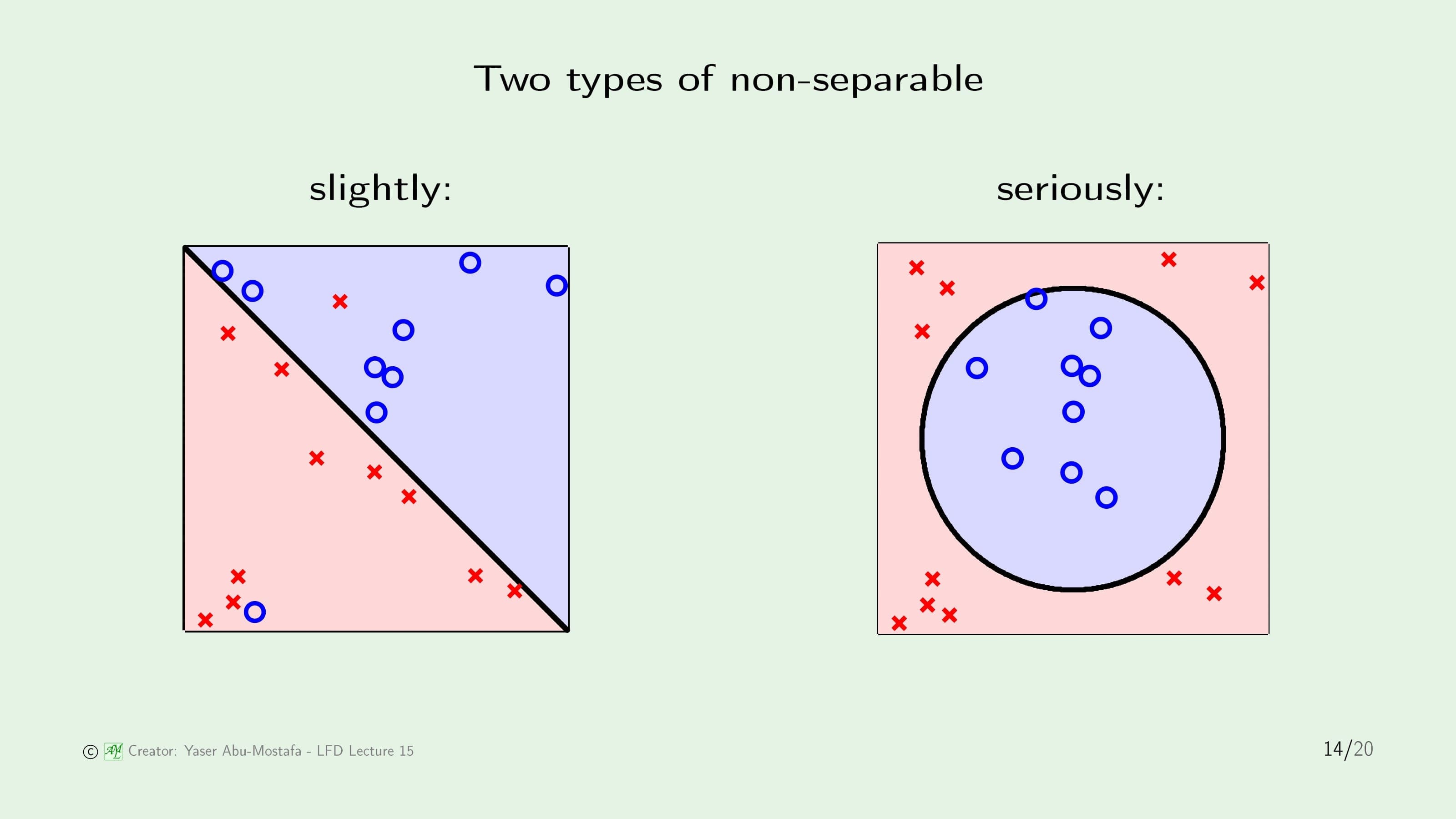
이전과 마찬가지로 비선형 문제를 다룰 것이지만, 비선형 문제도 두 가지 종류로 나눌 수 있습니다. 하나는 왼쪽 그림처럼 몇 개의 데이터만 무시한다면 선형으로 나눌 수 있는 경우고, 다른 하나는 오른쪽 그림처럼 아예 선형 분류를 시도조차 할 수 없는 경우입니다.

오른쪽 그림과 같은 경우는 Kernel로 처리하면 되지만, 왼쪽 그림과 같은 경우는 Kernel보다 더 나은 방법이 있을 것 같습니다. 이제 배울 Soft-Margin SVM으로 이런 경우를 처리할 것입니다.

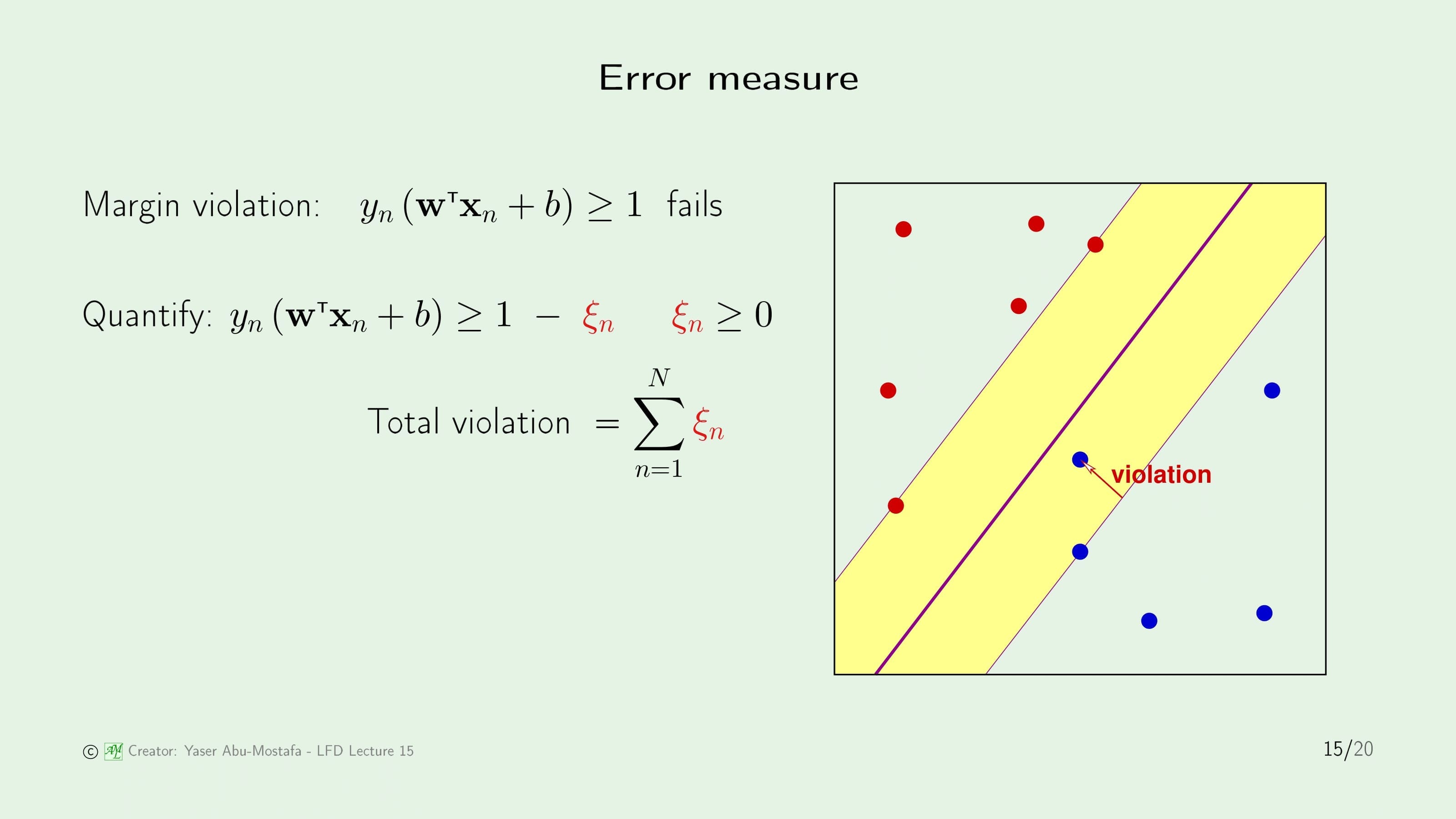
Support Vector Machine의 Error Measure를 다시 한번 살펴보겠습니다. 현재 문제가 되는 것은 Support Vector 사이에 있는 Margin 영역에 Violation (침범)하는 데이터입니다. 이 Violation 데이터 때문에 Support Vector를 구하는 식인 $y_n (\mathbf{w}^{\sf T} \mathbf{x}_n + b) \ge 1$가 성립하지 않습니다.

이 문제를 해결하기 위해 Violation 데이터를 정량화할 필요가 있고, 원래의 최적화 식을 변형해야 합니다. 오른쪽 항에 0보다 큰 $\xi_n$를 빼주는데, $\xi_n$의 총 합이 Violation이 일어나는 총 합이 됩니다.

Support Vector를 구하는 식을 바꾸었으니 원래의 최적화 식 또한 변경할 필요가 있습니다. 원래의 최적화 식에 $\xi_n$의 총 합과 그 가중치를 나타내는 상수 $C$를 곱한 값을 빼주어야 합니다. Augment Error의 개념과 비슷하다고 생각하시면 됩니다. 최적화 식의 조건은 이전 슬라이드에서 변경했던 식이 그대로 들어왔습니다.

최적화 식이 바뀌었으니, 그것을 계산하는 라그랑지안 또한 바뀔 것임을 쉽게 알 수 있습니다. 라그랑지안에서는 최적화 식과 조건을 하나의 식으로 만들어주므로 대부분의 항은 크게 문제 될 것이 없습니다. 마지막 항을 보시면 $\beta_n \xi_n$의 합을 빼는 항이 추가된 것이 보이는데, 이것은 $\xi_n$이 0보다 크다는 조건을 라그랑지안으로 표현한 것입니다.

라그랑지안에서 변수 $\xi_n$가 추가되었으니 라그랑지안을 $\xi_n$에 대해 편미분한 식을 구해야 합니다. 라그랑지안이 복잡해 보이지만, 자세히 보시면 라그랑지안이 $\xi_n$에 대해 죄다 1차식으로만 이루어졌다는 것을 알 수 있습니다. 따라서 남는 계수는 $C$와 $\alpha_n$, 그리고 $\beta_n$ 뿐입니다. 식은 간단하지만 의외로 이 편미분의 결과가 의미하는 바는 큰데, $\alpha_n$이 $C$보다 절때 클 수 없다는 것입니다. 만약에 $\alpha_n$가 $C$ 보다 크다면 편미분 식을 만족하는 $\beta_n$값이 없어지기 때문입니다. 게다가 이제 $\beta_n$을 $\alpha_n$과 $C$로 표현할 수 있으니, 추가된 새로운 변수인 $\beta_n$을 소거할 수 있습니다.

최종적으로 라그랑지안을 살펴보면 당연히 $\beta_n$는 이제 없어지고, $\alpha_n$이 $C$보다 크지 않다는 조건이 추가되었습니다.

이제 Support Vector의 종류를 살펴보도록 하겠습니다. 이제 이전과 달리 모든 Support Vector가 Magin을 나타내는 것이 아닙니다. 변경된 Support Vector를 구하는 식에서 $\xi_n$가 0인 경우에는 이전과 마찬가지로 Margin의 경계선에 위치하는 Support Vector가 나오지만, 그렇지 않은 경우에는 Support Vector가 전혀 엉뚱한 위치에 있을 수 있기 때문입니다.

마지막으로 두 가지 기술적 관점을 살펴보겠습니다. 원래의 Support Vector Machine은 데이터가 선형으로 분리가 가능한 경우를 가정해서 Hard Margin을 계산하는 것이었습니다. 그러나 데이터가 선형 분리가 되지 않을 때는 다른 방법을 찾아야 하는데, 쉬운 방법으로는 방금과 같이 Soft Margin을 구하는 것입니다. 이때 변수가 $\alpha$ 하나에서 $\beta$가 추가되었기 때문에 Dual Problem으로 바뀌게 됩니다.

두 번째로는 $\mathcal{Z}$ 공간에서의 문제입니다. 기존에 Threshold를 의미하는 $w_0$이 있었다는 것을 기억하실 겁니다. 그런데 SVM에서는 이에 대한 언급이 없고, 이와 비슷한 기능을 하는 $b$가 있었습니다. 같은 역할을 하는 서로 다른 변수가 있기 때문에 개념이 꼬일 수 있지만, 결과적으로 이 둘이 전부 0으로 수렴하기 때문에 실제 계산에서는 신경 쓸 필요가 없습니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.