Linear Models I

3장에서는 새로운 이슈인 Linear Model (선형 모델)에 대해서 알아보는 시간입니다.

Introduction에서도 언급했었지만, 본 교재와 강의자료의 순서가 다른 부분이 조금 있는데, 오늘 할 Linear Model 부분이 바로 그런 부분입니다. 교재에서는 Linear Model 파트가 한 장으로 묶여 있는데, 강의에서는 두 부분으로 나누어 앞부분을 3장에 넣고, 뒷부분을 9장에 배치하였습니다.

왜 이렇게 만들었는가 궁금했는데, 강의영상에서 말하길 이 장을 여기에 넣는 것이 적절하지 않지만, 이론 설명 후에 구체적인 예시를 주고 싶어서 앞에 끼워넣었다고 합니다. 그런 이유로 이 장은 이전 장과 다음 장과는 직접적인 관련은 없습니다만, 추후에 이어지는 내용이 나오기 때문에 확실히 짚고 넘어가셔야 할 것 같습니다.

Outline

이번 장의 순서는 크게 입력값의 표현을 어떻게 할 것인지부터 시작해서 Linear Classification (선형 분류), Linear Regression (선형 회귀)를 다루고 Nonlinear Problem (비선형 문제)을 해결하기 위한 접근 방법을 소개하며 끝나게 됩니다.

Input Representation

간단한 예제로 사람이 손으로 쓴 숫자를 분류하는 문제를 들어봅시다. (우체국에서 손으로 쓴 주소를 기계가 분류하는 시스템을 구축한다고 생각하시면 이해가 쉬울 것 같습니다) 입력값은 위의 슬라이드에 나온 대로 사람들이 직접 손으로 쓴 숫자들을 따와서 사용하게 됩니다. 첫 번째 문제로, 입력 데이터는 그림인데, 기계학습으로 처리하기 위해서는 이를 수치화 시켜서 표현할 필요가 있습니다.

그림 데이터를 수치화시키는 방법은 여러가지가 있지만, 일반적으로 컴퓨터는 그림을 픽셀의 묶음으로 처리하기 때문에 그림의 각 픽셀값을 입력으로 변환하는 방법을 생각해볼 수 있습니다. 이 예제의 경우, 한 숫자 그림이 차지하는 픽셀이 256개라고 가정했습니다. ($x_0$는 Threshold를 위해 만든 Input입니다 - 1장 참고)

Linear Classification의 대표적인 방법이 바로 1장에서 소개되었던 Perceptron Learning Algorithm (PLA)입니다. 이 예제를 PLA로 푼다고 가정했을 때, Input Vector의 크기만큼 Weight Vector가 필요하니까 Weight Vector도 256+1 차원 만큼이 필요함을 알 수 있습니다. 물론 이렇게 놓고 문제를 풀 수도 있지만, 이런 간단한 문제에 이렇게 차원이 큰 Vector를 사용하기엔 비효율적입니다. 데이터를 256차원으로 표현한다고 해봤자 의미없는 입력값이 너무 많고 (예를 들면 귀퉁이부분의 픽셀) 하려고 하는 분류 난이도에 비해 구해야할 Weight의 갯수가 너무 많아 학습이 매우 느리게됩니다.

그럼 이 데이터를 어떻게 간단하게 바꿀까요? 숫자의 모양을 이용한다면 0, 1, 8 같은 숫자는 대칭적이고 그 외의 숫자는 비대칭이니 대칭 여부를 통해 숫자를 1차적으로 분류하는 것도 문제를 간단하게 만드는 방법이 될 수 있습니다. 또한 1, 7에 비해서 8은 그림에서 차지하는 검은색 픽셀이 더 많습니다. 이것도 숫자를 분류하는 데 사용이 가능해 보입니다. 이 두가지 특징을 사용하여 Input Vector를 간단하게 2+1 차원으로 줄여봅시다.

Linear Classification

Input Vector가 $x_0$, $x_1$, $x_2$ 단 3개로 줄어든 걸 볼 수 있습니다. $x_0$의 역할은 이전과 마찬가지로 Threshold 역할이고, $x_1$은 검은색 픽셀의 밀집도, $x_2$는 대칭 여부를 의미합니다. 간단하게 바꾼 Input Vector로 숫자 1과 5를 분류해 보았습니다. 아무래도 1보다 5가 차지하는 검은색 픽셀이 더 많고, 숫자 1은 대칭적인데 비해 5는 대칭적이지 않으니 이 둘을 구분하는건 크게 어렵지 않아 보입니다.

다만 슬라이드의 그림을 자세히 보시면 대략적으로는 구분이 가능하지만, 몇몇 지점에서 약간의 Noise가 있음을 알 수 있습니다. 이 Noise 때문에 이 데이터는 Linearly Seperable 데이터가 아님을 알 수 있습니다. 1장에서 PLA는 Linearly Seperable 데이터가 아니라면 수렴하지 않는다고 했기 때문에 이 문제 또한 학습 결과가 수렴하지 않습니다.

실제로 이전 슬라이드의 데이터를 사용하여 PLA를 수행한 결과입니다. 왼쪽 그림은 데이터의 갯수가 증가할수록 In Sample Error와 Out of Sample Error가 어떻게 변하는지를 나타내고 있습니다. 정상적인 학습이라면 데이터의 갯수가 증가할수록 두 Error 모두 0으로 수렴해야하지만, 이 문제에서는 Linearly Seperable 데이터가 아니므로 수렴하지 않고 진동하는 모양의 그래프가 나옴을 알 수 있습니다. ($E_{in}$와 $E_{out}$의 변화를 참고하세요)

여기서 눈치가 빠르신 분은 어떻게 정확한 $E_{out}$을 표현한 것인지 궁금하실텐데, 물론 실제로는 $E_{out}$를 알지 못하지만, 이 예제에서는 $E_{in}$와 $E_{out}$가 어떤 관계가 있는지 보여주기 위해서 전체 샘플을 제한하여 계산하였습니다.

다행히도 이 문제에서는 $E_{in}$가 커지면 $E_{out}$도 커지고, 작아질 때도 같이 작아지는 비례 관계임을 알 수 있네요. (모든 문제가 그렇지는 않습니다. 이것은 아주 예외적인 경우입니다.) 즉, 앞으로는 $E_{in}$만 알아도 이를 낮추는 방향으로 설계를 한다면 $E_{out}$도 자연스레 줄어드는 결과가 나온다는 좋은 정보를 알게 되었습니다.

그런데 왼쪽 그림을 보니 수행 횟수가 1000번일 때의 Error가 250번 정도일 때보다 크게 나타납니다. 하지만 이 알고리즘은 1000번 수행 후의 결과를 출력하다 보니 이전에 더 좋은 성능을 보이는 Weight Vector를 찾았음에도 그보다 못한 값이 최종 값으로 확정되어버렸네요. 이걸 개선한다면 이전보다 좋은(=Error가 낮은) Weight Vector를 찾을 수 있어 보입니다.

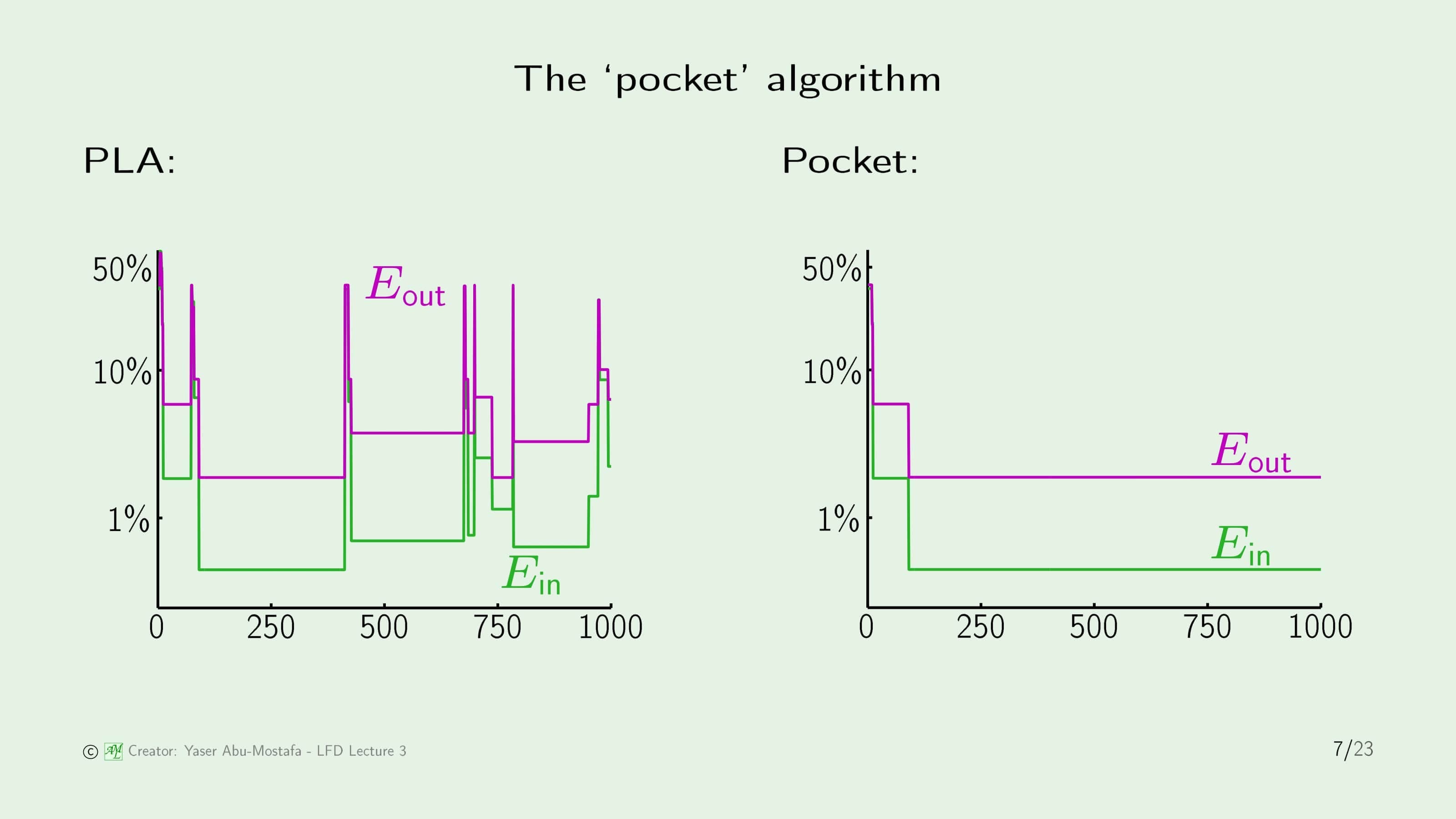
여기서는 이 문제를 Pocket Algorithm으로 해결합니다. Pocket Algorithm은 수행 중에 최고 성능을 보이는 Weight Vector 값을 저장해 두고, Weight Vector가 변경되었을 시 성능이 기존보다 떨어진다면 이를 반영하지 않는 알고리즘입니다. (좋은 것을 찾았을 때 주머니에 넣어두는 것을 떠올리시면 이해가 편할 것 같습니다.) 즉, Pocket Algorithm을 사용한다면 Weight Vector를 학습시킬수록 Error가 높은 (낮은 성능을 보이는) Vector가 나온다고 해도 항상 최선의 결과만 출력해 줄 수 있다는 장점이 있습니다. 왼쪽 그림을 보시면 데이터의 수가 100~400개 근처일 때 가장 성능이 좋고, 이후에는 계속 이보다 나쁜 성능을 가지는 Vector만 나오다 보니 Pocket Algorithm의 경우 100 즈음부터 변화가 없는 것을 알 수 있습니다.

위 슬라이드는 PLA를 사용한 결과와 Pocket Algorithm을 사용한 결과를 비교한 그림입니다. 검은색 줄이 1로 판단할 것인가 5로 판단할 것인가를 나누는 기준선입니다. Linearly Seperable 데이터가 아니기 때문에 두 그림 모두 완벽하게 판별하지는 못하지만, 확실히 Pocket Algorithm으로 나눈 결과가 더 바람직해 보인다는 것을 알 수 있습니다.

Linear Regression

지금까지 Linear Classification를 하는 방법을 알아보았습니다. 문제 난이도를 조금 올려, 이제 Linear Regression를 하는 방법을 알아보겠습니다. Regression (회귀)은 출력 결과가 +1/-1이 나오는 Classification와는 다르게, 출력 결과로 실수값으로 나오는 것을 말합니다.

1장에서 다루었던 카드를 발급하는 문제로 돌아와봅시다. 그때는 신청자의 정보를 바탕으로 카드를 발급해 줄 것인가/거부할 것인가의 여부를 다뤘다면, 이제는 카드 발급 여부에 더해 카드의 한도를 어떻게 정할 것인가를 구해야 합니다. 카드의 한도는 사람마다 다를 뿐더러 결과값이 실수(Real Number)로 나오기 때문에 이전보다 문제가 복잡해졌습니다. 지원자의 정보의 형태(Input Vector)는 분류를 할 때와 크게 다르지 않습니다만, 분류를 할 때와 달리 실수값의 출력이 나와야 하므로 Hypothesis $h$의 형태가 $sign()$ 함수를 떼버린 $\mathbf{w}^{\sf T} \mathbf{x}$ 꼴로 나오게 됩니다.

이전 슬라이드에서 언급했다시피 입력 값은 분류때와 큰 차이점은 없습니다. 다만 분류에서는 $y_n$의 값이 +1/-1이었지만 회귀에서는 실수 값이 들어간다는 것만 주의하시면 됩니다.

문제가 다르니 Error를 어떻게 측정할 것인가도 생각해 보아야합니다. 분류에서는 출력이 +1/-1 뿐이다 보니 그냥 정답과 다른 것의 갯수만 세면 충분했습니다. 그래서 전체 중에 몇개나 틀렸는지를 비율로 표시하였습니다.

하지만 회귀에서는 출력의 값이 무한정 많다보니 단순히 틀렸냐 틀리지 않았냐만을 따지기에는 곤란합니다. 예를 들어 정답 출력이 1000 인 입력값에 대해서, 950 정도 예측한 것과 5000으로 예측한 것은 둘다 틀린 결과값이지만 똑같이 오답으로 처리하기에는 무리가 있습니다. 950정도면 틀려도 감수할만한 값일 수 있지만, 5000은 도저히 용납이 불가능하기 때문입니다. 따라서 각 입력값에 대해 얼마나 “큰 차이”로 틀렸냐를 토대로 Error를 측정하게 됩니다. 이 “차이”를 측정하는 방법은 여러 가지가 있지만, 이 강의에서는 Hypothesis Function과 Target Function의 차이를 제곱한 값을 사용하게 됩니다.이를 Squared Error라고 합니다.

이걸 보시면 “단순한 차이를 원한다면 제곱할 필요 없이 그냥 차이의 절대값을 쓰면 되는게 아닌가?” 라는 의문이 드실 수도 있습니다. 제곱을 쓰는 데는 여러가지 이유가 있으나 대표적인 이유로는 절대값을 쓰게 되면 미분이 힘들어지기 때문입니다. 차이가 크면 클수록 패널티를 많이 주기 위함도 있습니다.

이 Error Measure를 그림으로 표현한 슬라이드 입니다. 왼쪽 그림은 Input Vector가 1차원일 때의 예시이며, 오른쪽 그림은 Input Vector가 2차원일 때의 예시입니다. 파란색 선(오른쪽 그림에서는 파란색 평면)이 의미하는 것은 Hypothesis Function $h$이고, 빨간색 선이 실제 분류값(Target Fucntion $f$의 값)과 예측한 결과 값의 차이입니다. 헷갈리실수도 있지만, 빨간색 선을 그릴 때 $h$에 대해서 직교하는 선을 그리는 것이 아님을 유의하셔야 합니다.

그럼 이 Error Measure를 통해서 $E_{in}$을 계산해봅시다. 입력값의 개수가 $N$이므로 모든 입력값에 대해 평균적인 차이를 계산한다면 아래와 같습니다.

\[E_{in}(\mathbf{w}) = \frac{1}{N} \sum_{n=1}^N (\mathbf{w}^{\sf T} \mathbf{x}_n - y_n)^2\]

식을 좀 더 간단하게 표현하기 위하여, $\mathbf{x}_n$들을 묶어 $\mathbf{X}$라는 큰 Vector로 표현해봅시다. 그리고 출력값인 $y_n$도 하나로 묶어 $\mathbf{y}$로 묶어보겠습니다. 이렇게 바꾸면 $\Sigma$(Sigma) 연산이 사라지고, Vector $\mathbf{X}$와 Vector $\mathbf{w}$의 곱 연산으로 간단하게 나타낼 수 있습니다. 따라서 아래와 같이 간단한 꼴로 표현이 됩니다.

\[E_{in}(\mathbf{w}) = \frac{1}{N} \lVert \mathbf{X}\mathbf{w} - \mathbf{y} \rVert^2\]

최종적으로 구하고자 하는 것은 $E_{in}$의 최소값입니다. 어떤 함수의 어디에서 최소값을 갖는지 구하는 방법은 그 함수의 도함수(Derivative)를 구해서 그 값이 0인 점을 찾으면 됩니다. (물론 모든 함수의 최소값이 도함수가 0인 점이라는 것은 아닙니다만, $E_{in}$ 함수는 볼록 함수(Convex Function)이므로 최소값입니다) $E_{in}$을 미분하려면 Vector Calculus를 알아야 하는데, 모르시는 분을 위해서 중간 과정을 조금 적어드리겠습니다. (저도 Vector Calculus를 제대로 배워본적이 없어서 틀린 부분이 있다면 댓글로 지적 부탁드립니다)

\[E_{in}(\mathbf{w}) = \frac{1}{N} \lVert \mathbf{X}\mathbf{w} - \mathbf{y} \rVert^2\]

위의 원래의 식에서 제곱을 없애기 위해 $\lVert \cdot \rVert$ 부분을 풀어 써 보겠습니다.

\[E_{in}(\mathbf{w}) = \frac{1}{N} (\mathbf{X}\mathbf{w} - \mathbf{y})^{\sf T} (\mathbf{X}\mathbf{w} - \mathbf{y})\]

위 식에서 전치행렬(Transpose Matrix) 기호 $\sf T$가 어디서 튀어나왔나 싶으실텐데 이것은 $\sf T$를 붙이지 않으면 행렬 곱을 할 수 없기 때문에 Vector 계산 중 붙여진 것이라고 생각하시면 됩니다.

()위에 붙어있는 $\sf T$가 보기 싫으니, $\sf T$를 () 안으로 넣어줍시다.

\[E_{in}(\mathbf{w}) = \frac{1}{N} (\mathbf{w}^{\sf T} \mathbf{X}^{\sf T} - \mathbf{y}^{\sf T}) (\mathbf{X}\mathbf{w} - \mathbf{y})\]

이 식을 전개한다면,

\[E_{in}(\mathbf{w}) = \frac{1}{N} (\mathbf{w}^{\sf T} \mathbf{X}^{\sf T} \mathbf{X} \mathbf{w} - 2 \mathbf{y}^{\sf T} \mathbf{X} \mathbf{w})\]

이렇게 쓸 수 있습니다. $E_{in}$은 $\mathbf{w}$에 대한 함수이므로 $\mathbf{w}$로 미분을 하게 되면($\nabla E_{in}(\mathbf{w})$) 아래와 같이 도함수가 0이 되는 $\mathbf{w}$를 찾는 문제로 바뀌게 됩니다.

\[\frac{2}{N} \mathbf{X}^{\sf T} (\mathbf{X}\mathbf{w} - \mathbf{y}) = 0\]

여기서 $\frac{2}{N}$은 의미없는 상수이므로 지워주게 되면,

\[\mathbf{X}^{\sf T} (\mathbf{X}\mathbf{w} - \mathbf{y}) = 0\]

괄호 ()를 없애기 위해 분배법칙을 사용해 전개해줍니다.

\[\mathbf{X}^{\sf T}\mathbf{X}\mathbf{w} - \mathbf{X}^{\sf T}\mathbf{y} = 0\]

$\mathbf{X}^{\sf T}\mathbf{y}$항을 오른쪽으로 넘겨주면,

\[\mathbf{X}^{\sf T}\mathbf{X}\mathbf{w} = \mathbf{X}^{\sf T}\mathbf{y}\]

왼쪽 항에 $\mathbf{w}$만 남기기 위해서는 $\mathbf{X}^{\sf T}\mathbf{X}$의 역행렬을 양쪽에 곱해주어야 합니다. 일단 $\mathbf{X}$ 자체는 정사각행렬(Square Matrix)이라는 보장이 없지만, 임의의 행렬에 대해서 그 행렬의 전치행렬을 곱해주면 정사각행렬이 되므로 $\mathbf{X}^{\sf T}\mathbf{X}$는 정사각행렬입니다. (임의의 행렬이 크기가 $n \times m$ 이라 했을 때, 이 행렬의 전치행렬은 $m \times n$이 되고, ($m \times n$ 행렬)($n \times m$ 행렬) 연산을 해주면 $m \times m$ 행렬이 나오므로 $m$과 $n$에 관계없이 무조건 정사각행렬이 됩니다)

이제 $\mathbf{X}^{\sf T}\mathbf{X}$ 행렬이 역행렬이 존재하는지 확인해야 하는데, 만약에 이 행렬의 역행렬이 존재하지 않는다면 위의 식 자체가 의미가 없어져 버리므로, 여기서는 있다고 가정하고 계산하겠습니다.

양쪽 항에 $\mathbf{X}^{\sf T}\mathbf{X}$의 역행렬을 곱해주면,

\[\mathbf{w} = (\mathbf{X}^{\sf T}\mathbf{X})^{-1}\mathbf{X}^{\sf T}\mathbf{y}\]

이 성립하게 됩니다. 여기서 $\mathbf{X}$와 관련된 항인 $(\mathbf{X}^{\sf T}\mathbf{X})^{-1}\mathbf{X}^{\sf T}$를 묶어서 $\mathbf{X}^{\dagger}$이라 한다면 아래처럼 깔끔하게 바뀌게 됩니다. $\dagger$ 기호는 대거(Dagger)라고 읽으시면 됩니다.

\[\mathbf{w} = \mathbf{X}^{\dagger}\mathbf{y}\]

여기서 $\mathbf{X}^{\dagger}$를 $\mathbf{X}$의 Pseudo-Inverse (의사역행렬)라고 합니다. 이런 이름이 붙은 이유는, 이 행렬은 $\mathbf{X}$의 역행렬이 아님에도 불구하고 역행렬처럼 $\mathbf{X}^{\dagger}\mathbf{X} = I$가 나오는 성질을 가지기 때문입니다.

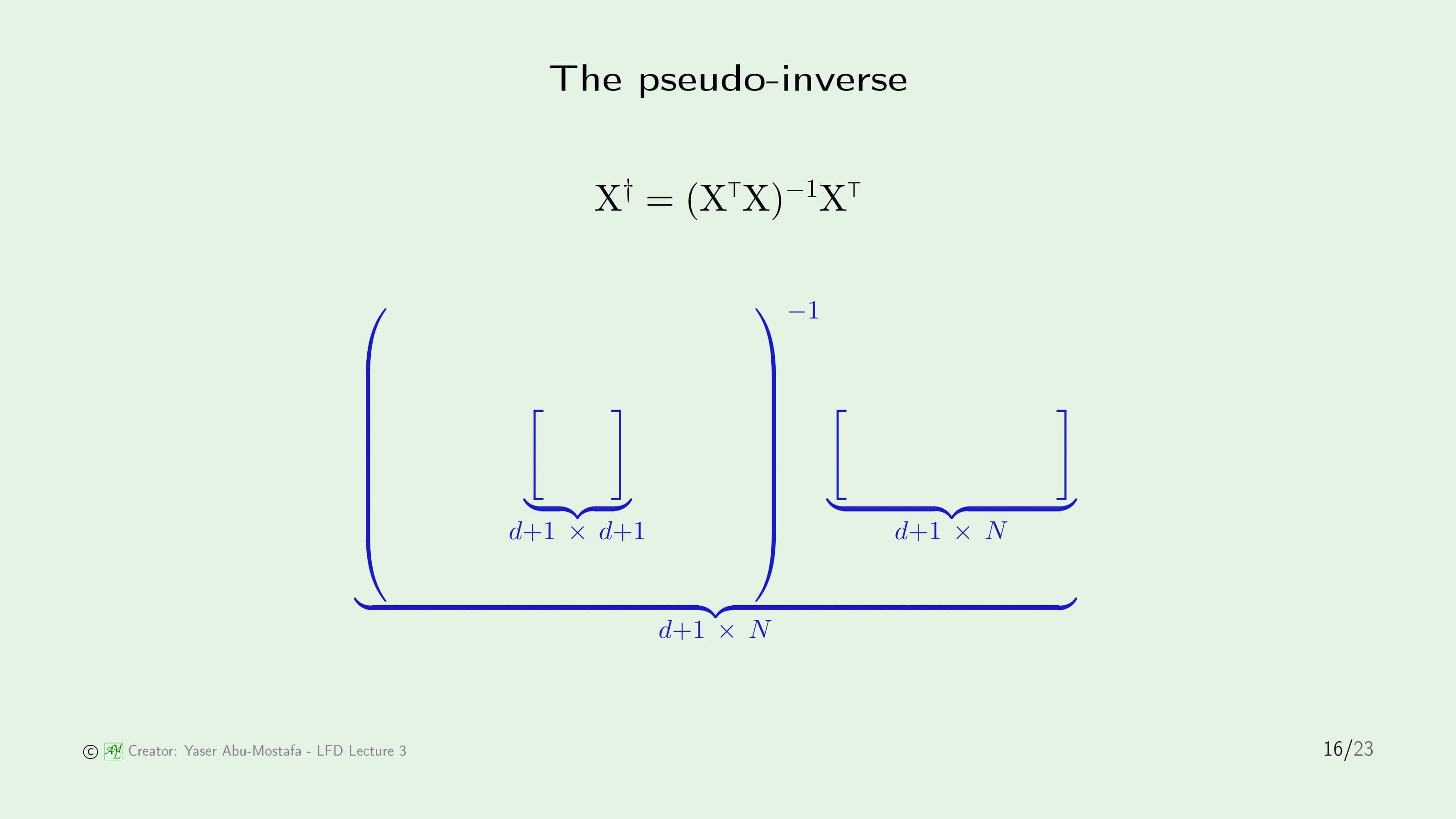
이전 슬라이드에 수식이 너무 많아 당황하셨을 수도 있지만, 걱정하지 않으셔도 됩니다. Pseudo-Inverse의 전개 과정을 안다면 더욱 좋겠지만 모르셔도 전체적인 이론을 이해하는데는 큰 무리가 없습니다. “회귀 문제를 풀기 위해서는 Pseudo-Inverse를 계산해야 하는구나” 정도만 아시면 됩니다. 어차피 요즘엔 MATLAB 등과 같은 수학 관련 프로그램이 모두 계산해주기 때문입니다.

이번에는 Pseudo-Inverse 행렬이 어떤 크기를 갖는지 알아봅시다. $\mathbf{X}$는 $d$차원의 입력이 $N$개 만큼 있으니 $N \times (d+1)$ 크기의 행렬이 될 것입니다. ($d$ 가 아니라 $d+1$ 인 이유는 Threshold를 나타내는 $x_0$가 포함되기 때문입니다) 그럼 $\mathbf{X}^{\sf T}$는 반대로 $(d+1) \times N$ 크기의 행렬이니 $\mathbf{X}^{\sf T} \mathbf{X}$ 를 계산한다면 $(d+1) \times (d+1)$ 크기의 행렬이 됨을 알 수 있습니다. 역행렬을 구한다고 해도 행렬의 크기는 변하지 않으니 $(\mathbf{X}^{\sf T} \mathbf{X})^{-1}$ 또한 $(d+1) \times (d+1)$ 크기의 행렬이 됩니다. $\mathbf{X}^{\sf T}$행렬은 $(d+1) \times N$ 크기라고 했으니 $(\mathbf{X}^{\sf T} \mathbf{X})^{-1} \mathbf{X}^{\sf T}$를 계산하면 최종적으로 Pseudo-Inverse $\mathbf{X}^{\dagger}$는 $(d+1) \times N$ 크기의 행렬이 된다는 것을 알 수 있습니다.

최종적으로 Linear Regression를 하는 알고리즘을 정리해보면, 첫째로 입력값과 그 정답을 나타내는 값을 각각 $\mathbf{X}$와 $\mathbf{y}$ 행렬로 묶어주고, 둘째로 Pseudo-Inverse $\mathbf{X}^{\dagger}$를 계산한다음, 마지막으로 Pseudo-Inverse $\mathbf{X}^{\dagger}$와 $\mathbf{y}$를 곱해주면 $\mathbf{w}$를 알 수 있게 됩니다.

이 과정을 보시면 한번만 계산하면 끝나기 때문에 Learning이 아니라고 생각하실 수도 있습니다. 다만 책의 저자이신 Abu-Mostafa 교수님께서는 꼭 PLA처럼 모든 데이터에 대해 하나하나 Weight Vector를 수정하는 것만이 Learning이 아니라고 합니다. 다시 말해서 어떻게 구하는지 그 과정은 별로 중요한 것이 아니라고 합니다.

Linear Regression은 결과 값이 실수로 나온다는 것을 알고 있습니다. 그런데 Linear Classification에서 나오는 결과는 +1/-1인데, 이것도 실수니까 회귀와 연관을 지을 수 있지 않을까 하는 생각을 해봅니다. Linear Regression을 조금 응용한다면 Weight Vector $\mathbf{w}$를 가지고 Linear Classification를 할 수 있지 않을까라는 겁니다.

안타깝게도 회귀와 분류는 그 목적이 다르기 때문에 그대로 사용할 수는 없습니다. 하지만 회귀에 사용한 데이터를 이용해 분류에 도움을 줄 수는 있습니다. 기존에 분류를 할 때 $\mathbf{w}$의 초기값을 무작위 값(혹은 Zero Vector)으로 정의하였지만, 회귀에서 사용했던 $\mathbf{w}$를 초기값으로 정하게 된다면 분류에 수렴하기까지 시간이 매우 단축되는 결과를 얻을 수 있다고 합니다.

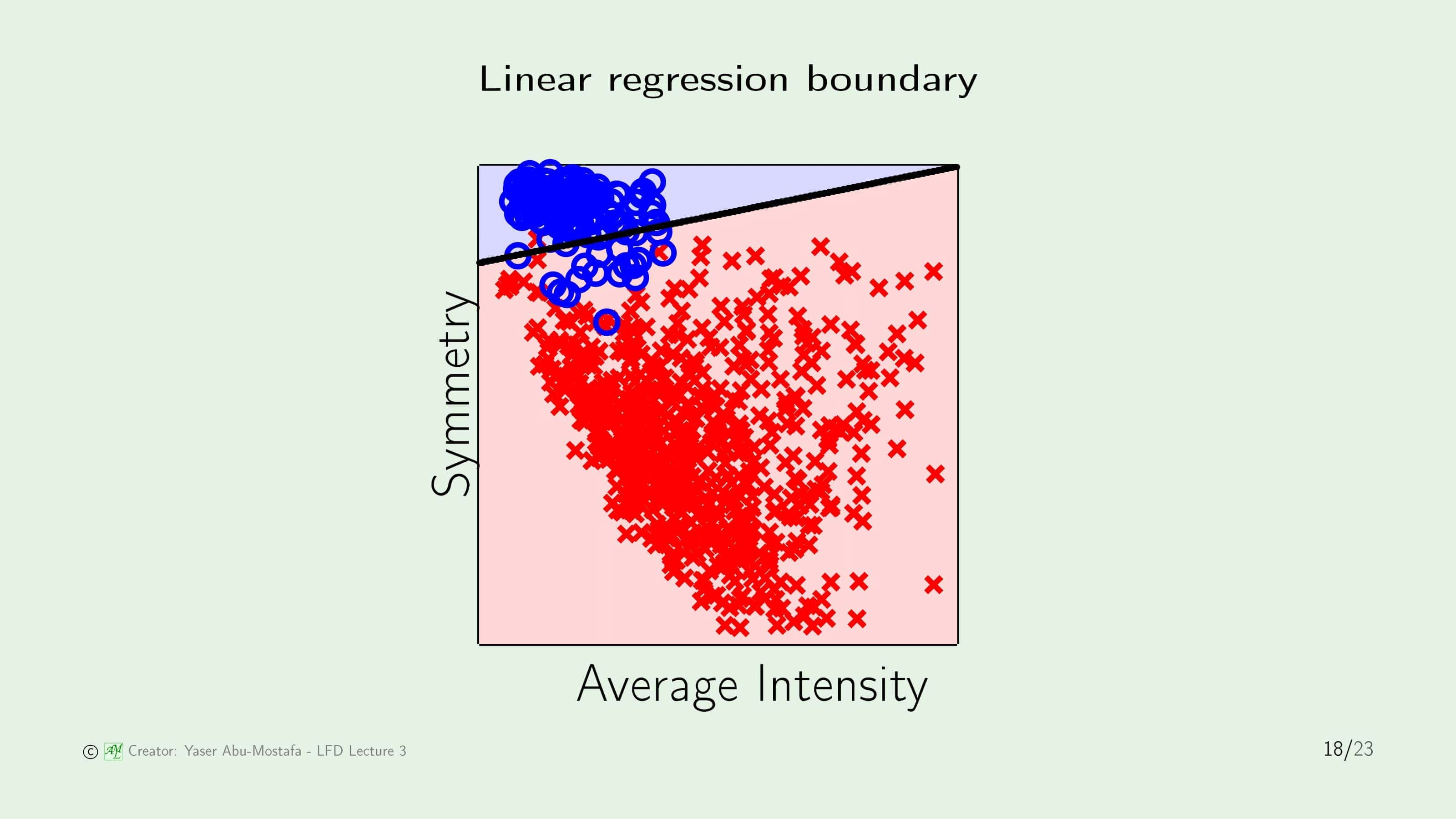
Linear Regression에서 구한 Weight Vector $\mathbf{w}$를 초기값으로 설정해 Linear Classification 문제의 그림으로 표현한 결과입니다. 완벽하지는 않지만, 정답과 매우 유사한 분류가 이루어졌음을 알 수 있습니다. 이 상태에서 시작해 PLA 등의 Linear Classification 알고리즘을 수행한다면, 많은 단계를 거치지 않아도 최적의 $\mathbf{w}$을 쉽게 구할 수 있겠구나라는 것을 예상할 수 있습니다.

Nonlinear Transformation

이제 마지막으로 Nonlinear Problem (비선형 문제)은 어떻게 접근하는지 알아봅시다.

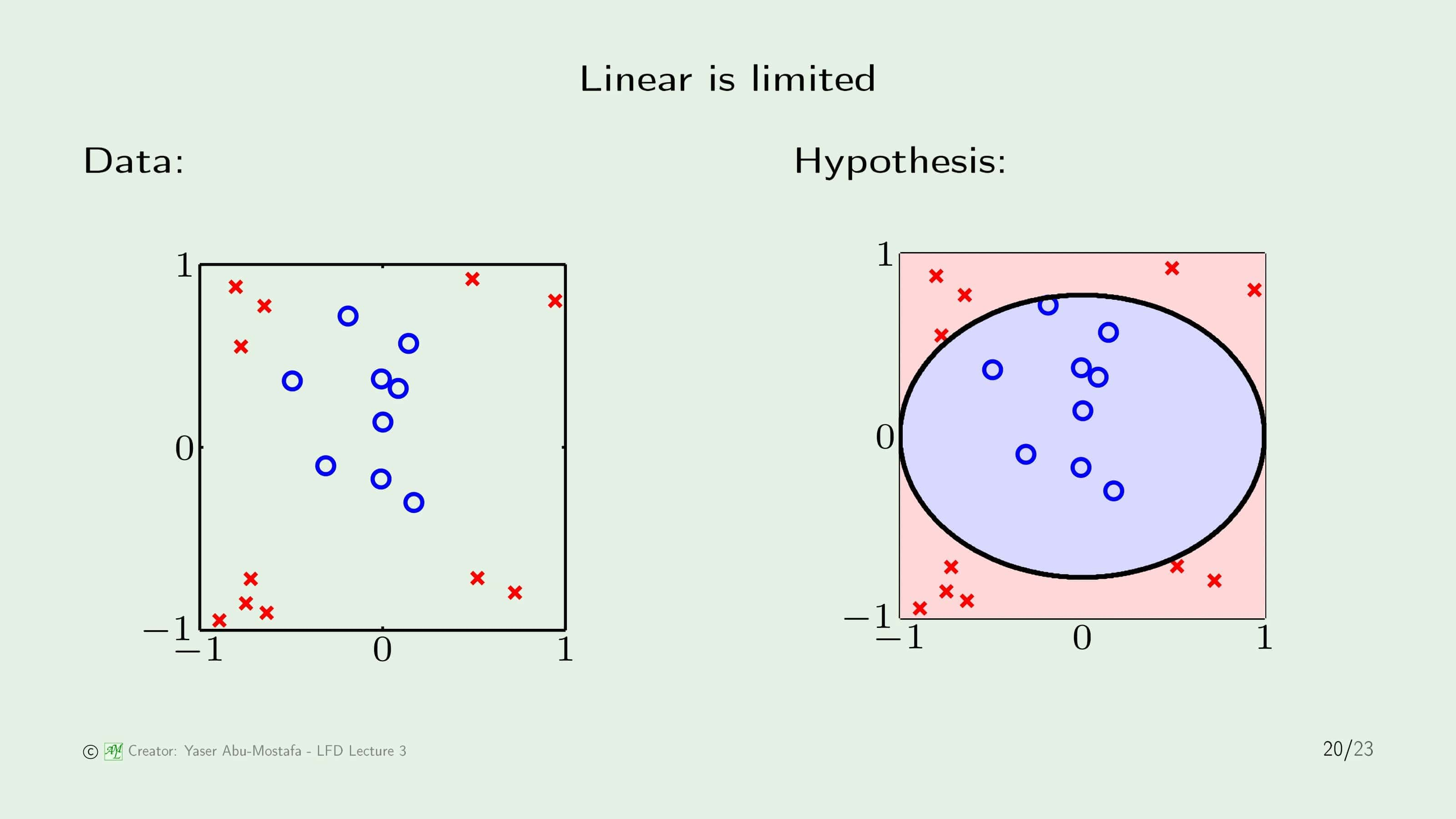
Linear Classification/Regression은 굉장히 편리하고 효과가 좋은 방법이지만, 안타깝게도 모든 문제가 Linear Model로 해결되지는 않습니다. 간단한 예제로 위 슬라이드의 왼쪽 그림과 같은 데이터의 경우, 어떻게 나누어도 직선으로는 분류할 수 없습니다. 오른쪽 그림처럼 원 모양으로 표현해야 제대로 나누어질텐데, Linear Model로는 저렇게 원 형태를 표현할 수 없는 것이 문제입니다.

잠시 카드 발급 문제로 돌아가서 “years in residence” 라는 요소를 생각해봅시다. 왜 그런지는 모르겠지만, 한 집에서 너무 적게 거주했거나(1년 미만) 너무 오래 거주한 경우(5년 초과) 부정적으로 평가한다고 합니다. 이런 경우 Linear Model을 통해 표현할 수 있을까요?

이 문제에 답을 하기 위해서는 “무엇”에 대해 Linear하냐 라는 것부터 생각해보아야 합니다. Input이 Linear이기 때문에 Linear Model이라고 생각하시는 분들이 있는데, Linear Model이라고 이름이 붙은 이유는 Weight에 대해 Linear이기 때문에 Linear Model이라고 부르는 겁니다. 그러니까, 다시 말해서 입력값 $\mathbf{x}$은 Linear이든 아니든 크게 상관이 없다는 겁니다.

그럼 입력값이 Linear일 필요는 없다고 했으니, 입력 값을 한번 바꾸어봅시다. 임의의 함수 $\Phi$를 정의해서 입력값 $\mathbf{x}$ 제곱하는 연산을 수행하게 만들어 봅시다. 위 슬라이드의 왼쪽 그림은 20번 슬라이드에 나왔던 그 예제입니다. 그런데 모든 데이터에 대해 $\Phi$ 함수를 거친 결과값을 표현하니 오른쪽 그림처럼 변했습니다. 이 바뀐 데이터의 분포는 Linearly Seperable 데이터라는 것을 쉽게 알 수 있습니다.

이런 방법을 통해 Linearly Seperable 데이터가 아닌 경우 임의의 함수를 정의하여 데이터를 변환시킴으로써 Linearly Seperable 데이터로 바뀌지만, 여기에는 한 가지 문제가 있습니다. 위의 그림처럼 간단한 예제의 경우에는 적당한 함수 $\Phi$를 쉽게 구했지만, 일반적인 상황에서는 적절한 $\Phi$를 찾는 것이 쉽지 않습니다. 그렇기에 또다른 방법이 필요하지만, 이 문제에 대한 해결 방법은 추후에 다시 언급됩니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.