Overfitting

11장은 Overfitting에 대해 배우게 됩니다. 단어의 뜻만 봐도 이게 무엇을 의미하는지 대충 알 수 있습니다. 예를 들면 옷 가게에서 Fitting Room은 옷이 자기한테 잘 맞는지를 확인하는 곳입니다. Fit의 의미는 맞다이고 Over는 무언가 과다한 상태의 형용사이기 때문에, Overfit은 과다하게 맞다라고 해석이 가능합니다. 기계학습에서 Overfitting도 이와 비슷한 의미입니다.

Outline

이번 장의 구성은 4개 부분으로 나뉘어 있습니다. 먼저 Overfitting이 무엇인지부터 배우고, 4장에서 배웠던 Noise가 무슨 역할을 하는지 알아본 뒤, Deterministic Noise를 배우고 마지막으로 Overfitting 문제를 해결하기 위한 방법을 알아봅니다.

What is overfitting?

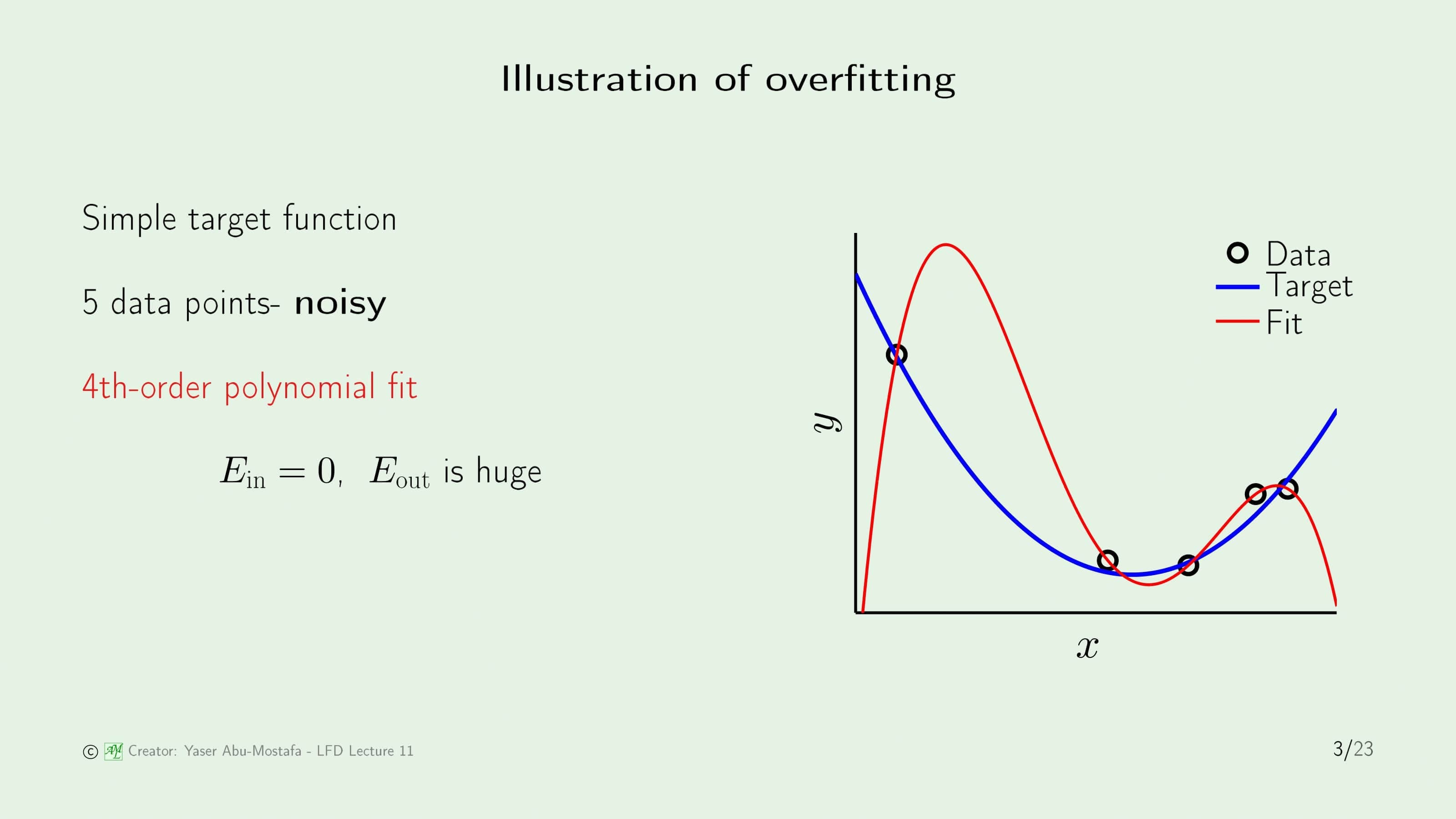
먼저 Overfitting이 일어나는 상황부터 한번 살펴보겠습니다. 간단한 예제로, 2차함수와 비슷하게 생긴 Target Function (파란색 선)이 있습니다. 데이터는 물론 이 Target Function으로부터 나오는데, 이 데이터가 완벽하게 Target Function 위에 있지 않고 어느정도의 Noise가 끼어 있는 상태로 주어집니다. 5개의 점이 주어졌으니, 이를 완벽하게 커버하기 위해서는 4차함수가 필요합니다. 그렇게 해서 4차함수를 사용해 In Sample Error가 0이 되도록 함수를 구한다면, 주어진 데이터는 완벽하게 커버할지 몰라도, Out of Sample Error는 엄청나게 커지는 문제가 발생합니다.

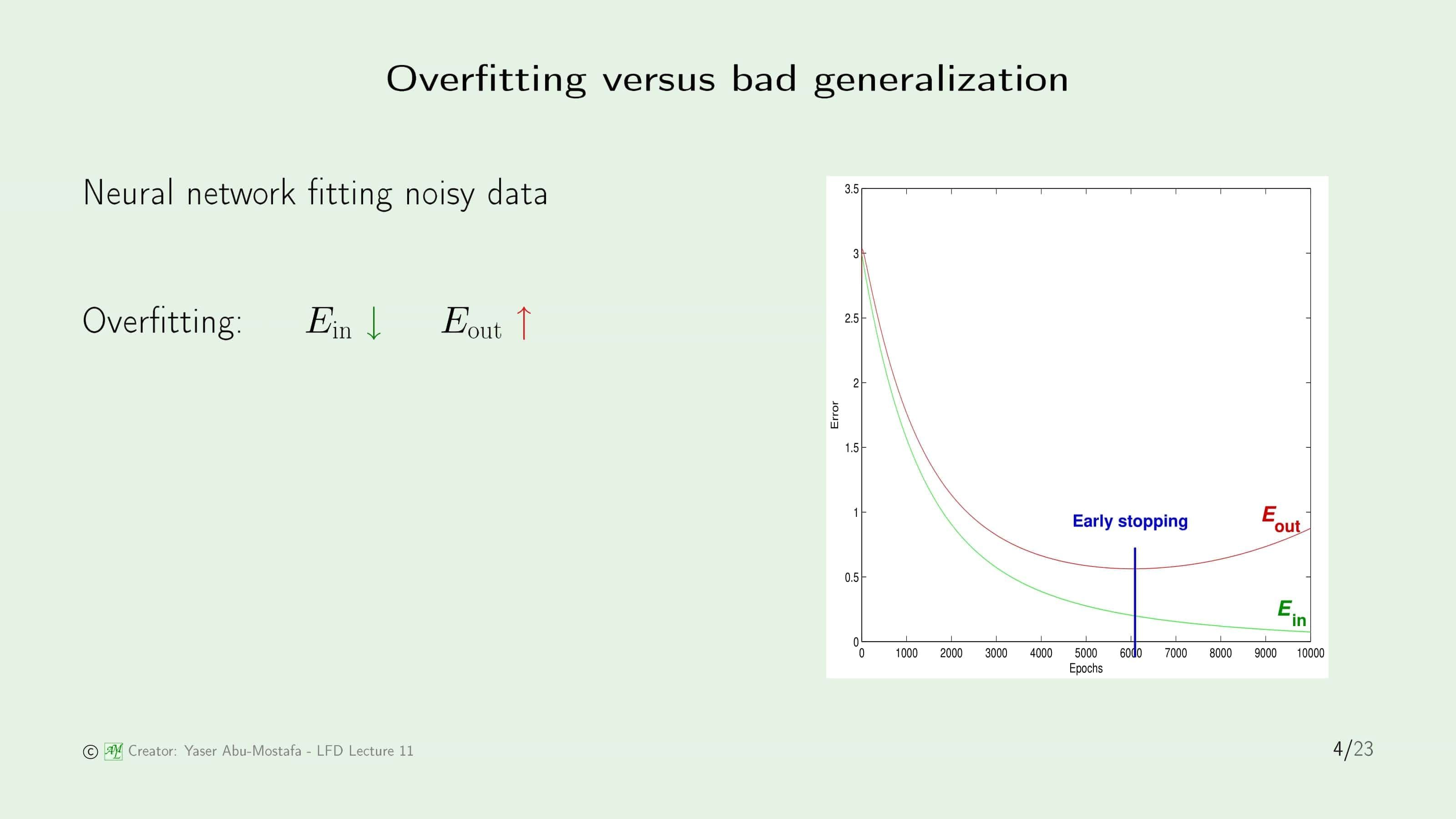
그렇다면 “Overfitting”과 “Bad Generalization”의 차이가 무엇인지 알아봅시다. Noise가 있는 데이터를 인공신경망 모델로 학습했을 때의 In Sample Error와 Out of Sample Error를 구합니다. 가로축은 학습횟수를 나타내고 세로축은 에러를 나타냅니다.

가로축의 0과 1000 사이를 보시면 In Sample Error와 Out of Sample Error 모두 에러가 매우 높게 나온 것이 보입니다. 이렇게 두 Error가 모두 높은 상황은 아직 모델이 데이터를 커버하지 못하는, 즉 일반화가 나쁜 상황이 됩니다.

반대로 가로축이 6000을 넘긴 시점을 보시면, 학습을 하면 할수록 In Sample Error가 줄어드는데, Out of Sample Error는 반대로 증가하는 모습을 보입니다. 이 때는 모델이 Sample 데이터에 과도하게 맞추고 있다는 것을 보여주므로, 이런 상황을 Overfitting이라고 부릅니다.

Overfitting이 일어나는 이유는 데이터를 보장된 만큼보다 더 맞추려고 하기 때문입니다. 이 말은, 데이터에 Noise가 있다면 그것까지 굳이 맞추려고 할 필요가 없는데도 불구하고 완벽하게 맞추려고 한다는 것입니다.

슬라이드 3을 예로 들면 데이터에 Noise가 있는 것을 알았을 시, In Sample Error가 어느정도 발생하는 것을 감수하고 2차함수로 모델링을 한다면 Overfitting이 일어나지 않지만, Noise까지 완벽하게 맞추려고(fit) 4차함수로 모델링을 하기 때문에 Overfitting이 발생하는 것입니다.

The role of noise

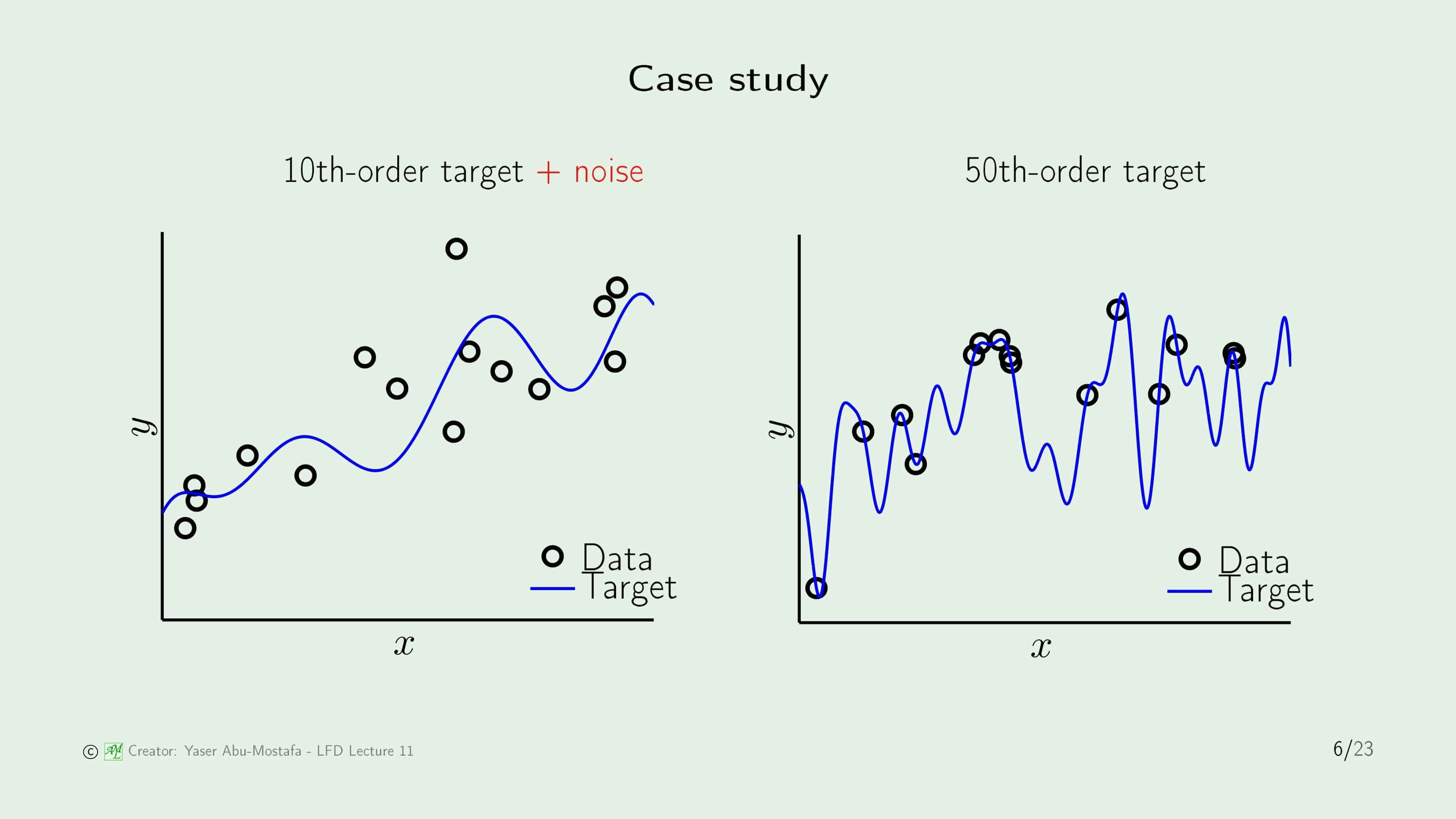
조금 더 복잡한 상황에서 살펴봅시다. 왼쪽의 예제는 Target Function이 10차 방정식인데, 주어진 데이터에 Noise가 끼어있는 상황이고, 오른쪽의 예제는 Target Function이 50차 방정식인데, 주어진 데이터에 Noise는 없는 상황입니다. 데이터는 두 모델 각각 15개씩 주어졌습니다.

이 두 예제는 2가지의 모델로 해결해 봅시다. 하나는 2차 방정식 모델이고, 다른 하나는 10차 방정식 모델입니다. 각 예제의 그림에서 초록색 선이 2차 방정식 모델로 해결한 결과이고, 빨간색 선이 10차 방정식 모델로 해결한 결과입니다. 놀랍게도 2차 방정식 모델이 두 예제에서 모두 10차 방정식 모델보다 훨씬 좋은 결과가 나왔습니다.

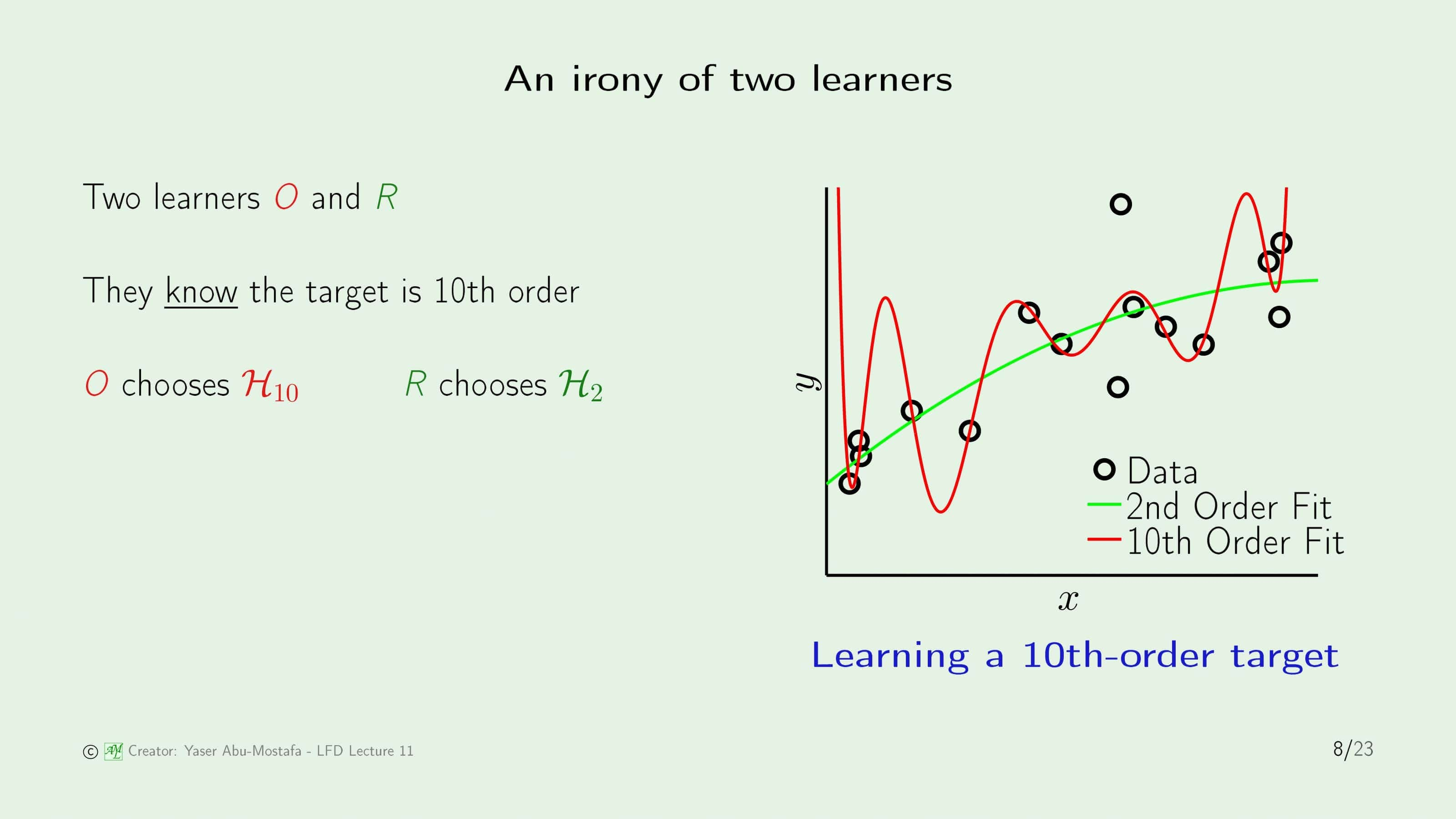
이전 슬라이드의 결과를 보면 의문이 듭니다. 첫번째 예제의 Target Function은 10차 방정식이였기 때문에 학습 모델을 10차 방정식으로 잡는 것은 상식적으로 생각해봤을때 전혀 과도하게 잡은 모델이 아닙니다. 오히려 2차 방정식으로 모델을 잡은 것이 너무 낮은 차수로 잡은 것이 아닌가 하는 생각을 들게 만들죠. 그렇다면 왜 이러한 결과가 나온 것일까요?

그 이유는 바로 데이터의 수가 적었기 때문입니다. 7장에서 배웠듯이, 올바른 학습을 위해서는 VC Dimension의 10배 만큼의 데이터가 필요하다고 하였습니다. 물론 2차 함수 모델의 VC Dimension은 3이므로 30개가 필요한데 비해 데이터는 그것의 절반밖에는 주어지지 않았지만, 10차 함수 모델의 필요한 데이터의 수인 110개보다는 가까웠기 때문에 더 좋은 성능이 나온 것입니다. 즉, 학습 모델을 잡을 때는 Target Function 보다 주어진 데이터의 수에 맞추는 것이 훨씬 더 좋은 성능이 나오게 됩니다.

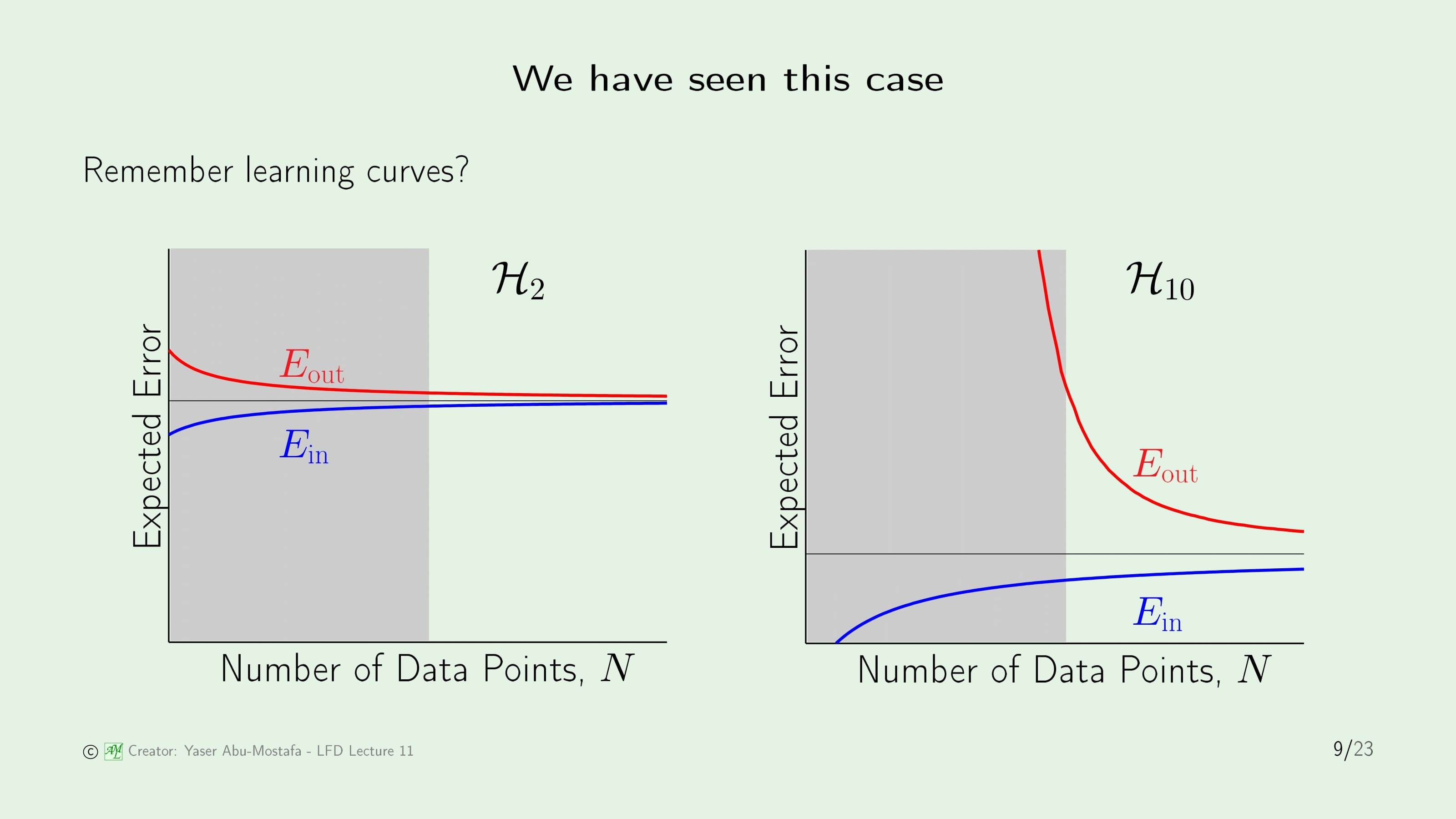
우리는 이미 이 사실을 이전에 배웠습니다. 데이터의 수가 충분하다면 물론 Target Function의 차수와 가까운 10차 방정식 모델 $\mathcal{H}_{10}$이 $\mathcal{H}_{2}$보다 성능이 좋게 나올 것입니다. 그러나 주어진 상황에서는 데이터가 매우 적은 상황이었기 때문에 회색 영역이 현재의 상황을 나타내는 부분이 되고, 데이터가 적은 상황에서도 In Sample Error와 Out of Sample Error의 간격이 적은 2차 방정식 모델이 그렇지 않은 10차 방정식 모델 보다 아직은 좋은 퍼포먼스를 보이게 되는 것입니다.

그렇다면 Target Function이 50차 방정식이고 Noise가 없었던 두 번째 예제로 넘어가 봅시다. Noise가 없는 상황이기 때문에 Overfitting은 일어나지 않을 것이라 생각되어 복잡한 모델인 $\mathcal{H}_{10}$이 이길 수 있을 것처럼 보이지만, 실제로는 여전히 $\mathcal{H}_{2}$가 더 나은 성능을 보여주고 있습니다. 왜 그렇게 되는지 알아보기 전에, 과연 이런 상황을 Noise가 정말로 없다고 부를 수 있을까요?

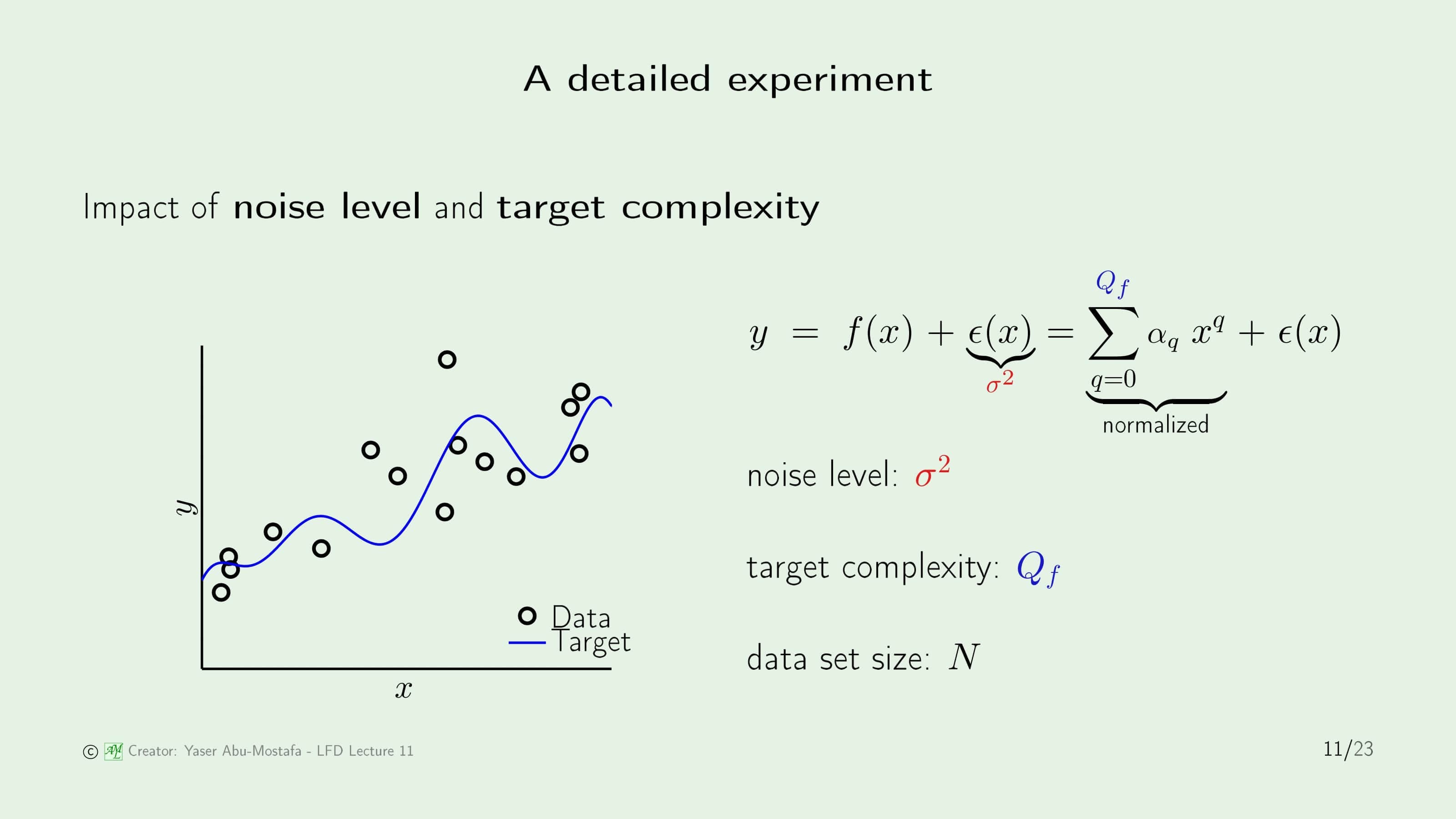
그 질문에 답하기 위해 좀 더 구체적인 실험을 해봅시다. Input을 간단하게 1차원 $x$라 하고 Output을 $y$라고 한다면 Noise가 없는 Input과 Output의 관계는 $y=f(x)$가 됩니다. 여기에 Noise Function $\epsilon(x)$를 더해주면, Noise가 추가된 Output $y$의 식이 됩니다. Noise는 일반적으로 가우시안 분포를 따르기 때문에 Noise의 정도를 나타내기 위해 이를 $\sigma^2$으로 표현합니다.

문제를 구체적으로 하기 위해 Target Function은 다항함수라고 가정하고, 최대 차수를 $Q_f$라 정의합니다. 그렇게 되면 $x$의 각 항에 계수가 붙는 다항함수 꼴을 시그마로 표현할 수 있습니다. 그리고 데이터의 수를 $N$으로 정의합니다.

방금 정의한 기호를 사용하여 하단 왼쪽에 있는 예제를 예로 들면, $Q_f=10$인 Target Function에서 $N=15$개의 데이터가 $\sigma^2$의 Noise를 따르도록 나타낸 것입니다.

이를 가지고 Overfit을 측정해봅시다. $N$개의 데이터 $(x_1, y_1), \ldots, (x_N, y_N)$를 사용하여 2개의 모델 $\mathcal{H}_{2}$과 $\mathcal{H}_{10}$로 학습한 결과를 비교해야 합니다. 비교는 각각의 모델에서 가설을 가지고 Out of Sample을 계산한 뒤, 그 차이를 구하는 것입니다.

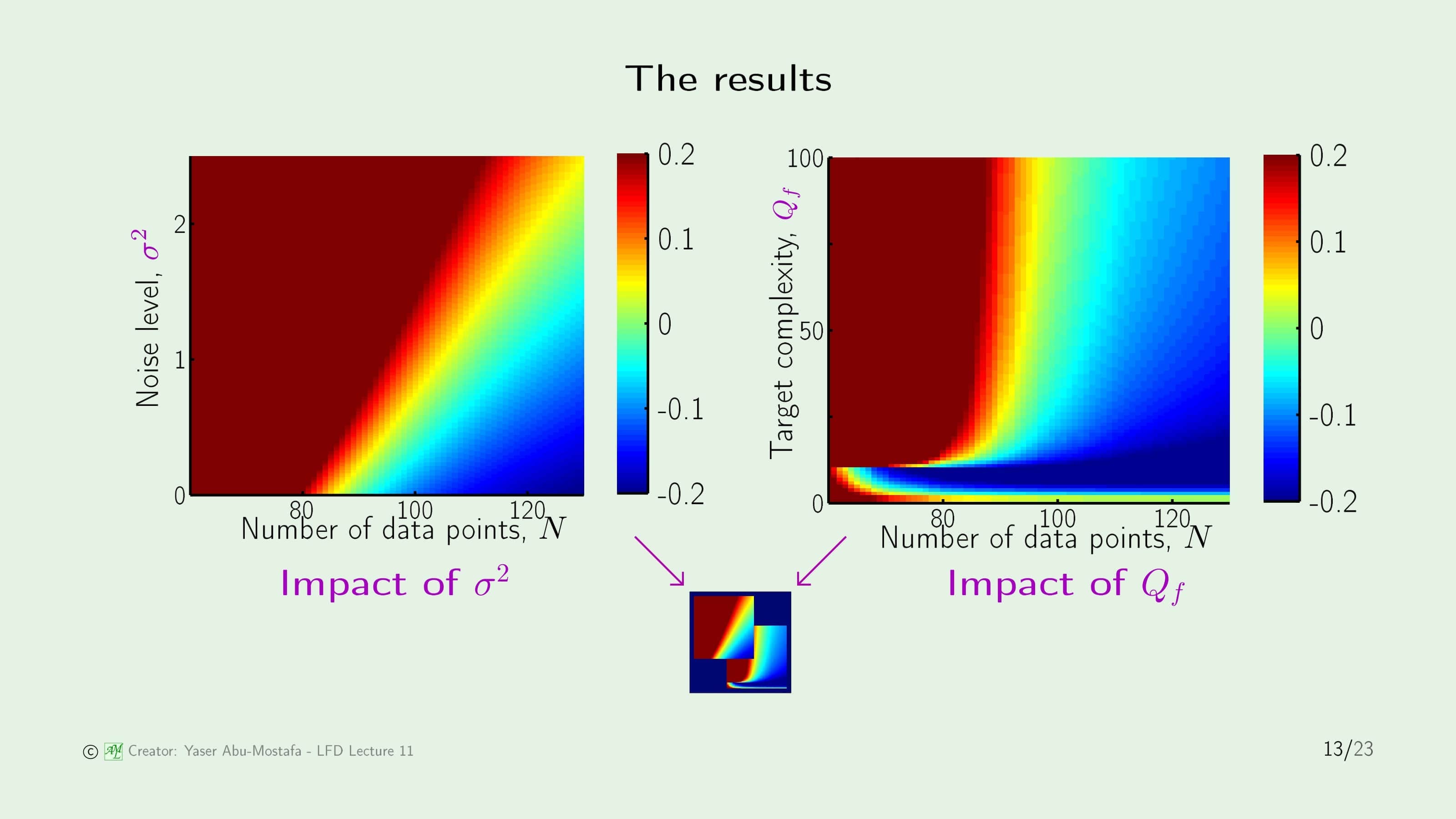
이 슬라이드는 그 결과를 표현하고 있습니다. 이 그래프는 무지개색으로 그 값이 어느정도인지를 표현하고 있는데, 색이 빨간색에 가까울 수록 Overfit Measure가 커지고(즉, $E_{out}(g_{10}) \gg E_{out}(g_2)$) 파란색에 가까울수록 Overfit Measure가 작아지는(즉, $E_{out}(g_{10}) \ll E_{out}(g_2)$) 상황입니다. 초록색인 상황은 두 가설에서의 Out of Sample이 동일하다는 뜻(즉, $E_{out}(g_{10}) = E_{out}(g_2)$) 입니다. 여기서 알아야 할 것은 빨간색이 짙을 수록 Overfitting이 심하게 일어난다는 뜻입니다.

먼저 왼쪽의 Noise Level의 변화에 따른 그래프를 봅시다. Noise Level이 클수록, Overfitting을 해결하기 위한 데이터의 수가 더 많이 필요한 것을 알 수 있습니다. 예를 들어, Noise Level이 0일 때는 100개의 데이터가 주어졌을 때 Overfitting이 일어나지 않지만, Noise Level이 2일 때는 똑같이 100개의 데이터가 주어졌을 때 Overfitting이 일어나기 때문입니다.

왼쪽의 그래프는 단순해보이지만, 오른쪽의 그래프는 조금 복잡해보입니다. 오른쪽의 그래프는 Target Function의 복잡도(즉, 다항함수의 차수)가 Overfitting에 미치는 영향을 나타냅니다. 먼저, $Q_f$가 커지면 커질수록 Overfitting이 심해지는 것은 간단하게 알 수 있습니다. 특이한 점은 $Q_f$가 일정 수치 이하일 때는 복잡도가 높아질수록 Overfitting이 일어나지 않는데, 뒤에 나올 슬라이드 17에서 그 이유가 나옵니다.

여담으로 이 두 그래프는 교재의 표지 하단 왼쪽에 나와있는 그림과 같습니다. 또한 매 강의 슬라이드 첫장 하단 왼쪽에도 동일한 그림이 나와있습니다.

이 실험으로 알게 된 것은 Noise Level과 Target Complexity 모두 Overfitting을 증가시킨다는 사실입니다. Noise Level $\sigma^2$은 어떤 확률 분포를 따르는 Noise이므로 이를 Stochastic Noise라고 부르고, Target Complexity는 확률적인 부분이 아니기 때문에 이를 Deterministic Noise라고 부릅니다. 이것을 Noise라고 부르는 이유는 실제 기계학습에서는 Target Complexity를 알 수 없기 때문에 마치 Noise처럼 보이기 때문입니다.

요약하자면, 데이터의 수를 증가시킬 수록 Overfitting은 감소하고 Stochastic Noise나 Deterministic Noise를 증가시키면 Overfitting 또한 증가한다는 결론을 낼 수 있습니다.

Deterministic noise

이제는 Deterministic Noise에 대해 좀 더 알아보겠습니다.

Deterministic Noise는 Stochastic Noise와 마찬가지로 가설 집합 $\mathcal{H}$가 알 수 없는 요소입니다. 알 수 없다는 것은 학습을 하면서 “이것이 Noise다!” 라고 분별할 수 없음을 뜻합니다.

오른쪽 그림은 Target Function $f$와 그 $f$를 최대한 가까운 근사 함수 $h^{*}$를 구한 모습인데, 보시다시피 어느정도의 차이가 있습니다. 그 이유는 그림에서 알 수 있다시피 $h^{*}$의 차수가 $f$보다 낮기 때문입니다.

만약에 $\mathcal{H}$가 더 큰 차수의 모델이었다면, 그 오차가 줄어듬을 알 수 있습니다. 이를 통해, Deterministic Noise는 $\mathcal{H}$에 따라 달라진 다는 것을 알 수 있습니다. 또한 학습을 주어진 데이터로 하기 때문에, 데이터가 동일하다면 학습 결과와 $h^{*}$ 또한 동일하므로, Deterministic Noise 또한 변하지 않는다는 특징이 있습니다.

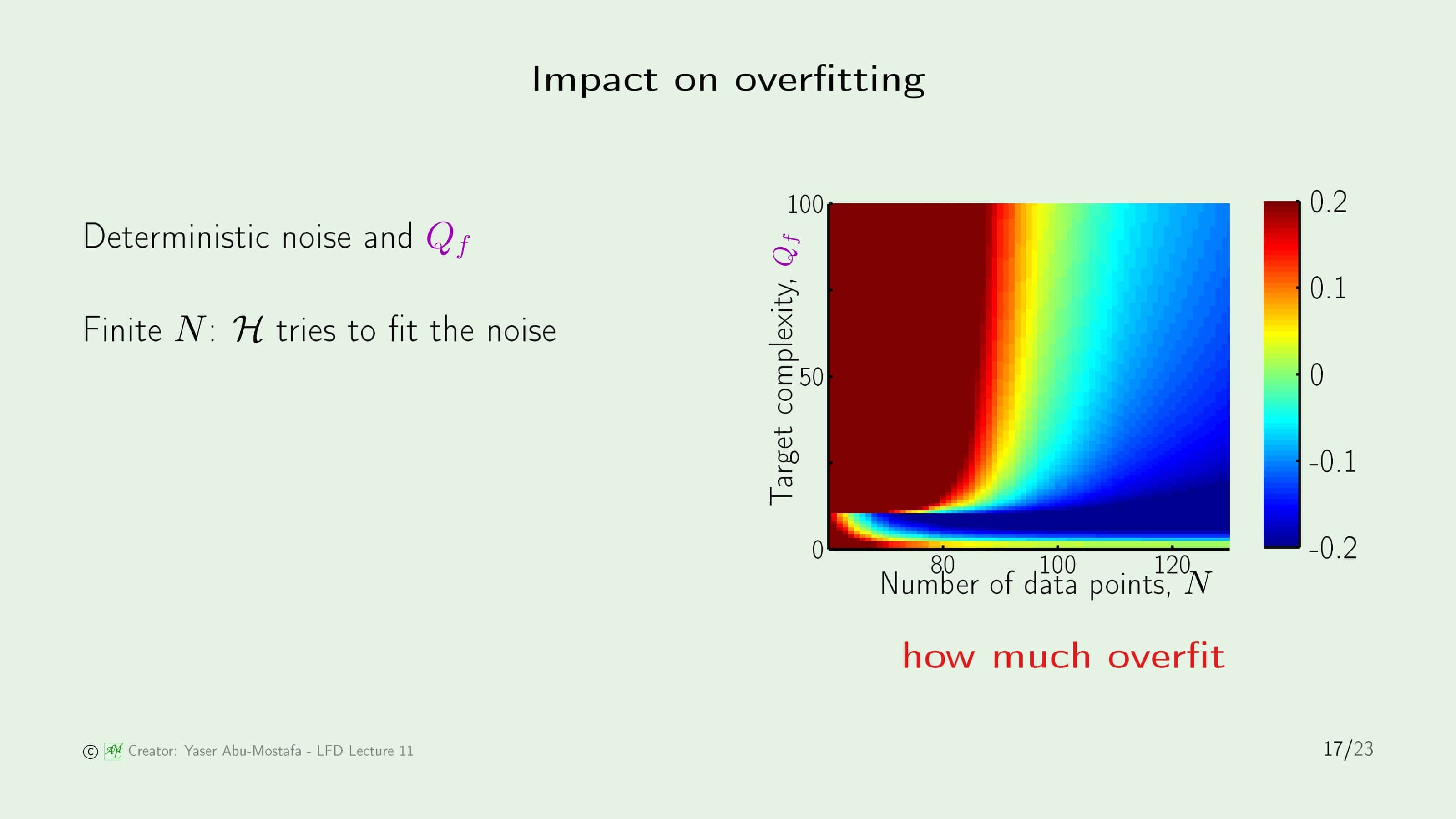
그렇다면 Deterministic Noise가 Overfitting에 끼치는 영향을 살펴보겠습니다. 오른쪽의 그림은 이전 슬라이드에서 본 그림인데, 그때 느낀 이상한 점은 $Q_f$가 일정 이하(여기서는 10)일 때는 Target Complexty가 커져도 Overfitting이 일어나지 않는 것이었습니다.

저 일정 이하의 부분에서는 Target Function보다 낮은 차수이기 때문에 Target Complexity를 높일 수록 Overfitting을 피할 수 있는 것입니다. (물론 일정 이상의 데이터가 필요하다는 것도 그래프를 통해 알 수 있습니다.)

그림을 통해 분석해 보았으니, 이제 수식을 통해 좀 더 정밀하게 분석해 보겠습니다. 8장에서 배웠던 Bias와 Variance를 기억하시나요? 이 분석 방법은 샘플에서 벗어난 오차를 Bias와 Variance로 각각 분류하였습니다. 이 당시 분석에서는 $f$에 Noise가 있다고 생각하지 않았습니다. 만약에 $f$에 Noise를 추가하게 된다면 식이 어떻게 바뀔 지 알아봅시다. Noise는 Gaussian Distribution (정규분포)을 따르기 때문에 그 평균은 0이라고 가정하겠습니다.

$y = f(\mathbf{x}) + \epsilon (\mathbf{x})$로 놓고 나머지는 8장에서 했던 전개 과정을 그대로 수행하였습니다. 식은 다행히 그렇게 어렵지 않은데, 그 이유는 Noise의 평균이 0이기 때문에 Noise와 다른 항을 곱한 Cross Term의 평균 또한 모두 0이 되어버리기 때문입니다.

즉, 최종적으로는 기존의 Variance와 Bias에 $\epsilon(\mathbf{x})$를 제곱한 평균만 추가되는 꼴이 됩니다. 그 마지막 항이 바로 Stochastic Noise가 됩니다. 그런데 Bias는 최선의 가설 $\bar{g}$가 Target Function과의 차이를 뜻했는는데 이것이 바로 Deterministic Noise의 정의와 같기 때문에, 여기서 이를 같은 용어로 치환합니다.

Dealing with overfitting

그렇다면 이제 Overfitting을 해결하는 방법을 알아보겠습니다. 불행하게도, Overfitting은 쉽게 해결되는 문제가 아니기 때문에, 이번 장에서는 어떤 방법들이 있는지만 소개하고, 그 방법들은 다음 2개의 장에서 하나씩 자세하게 설명합니다.

첫 번째로 Regulatization (정규화)라는 방법이 있습니다. 이는 학습 중간에 제동을 거는 방법인데, 구현 방법은 목적 함수 자체를 약간 변형시키는 방법을 사용합니다.

두 번째 방법은 Validation (검증)입니다. 위의 슬라이드 4를 보시면 Early Stopping 이라는 부분에서 멈춘다면 Overfitting이 일어나지 않음을 알 수 있습니다. 이 부분을 찾아서 멈추는 것이 바로 Validation이라는 방법입니다.

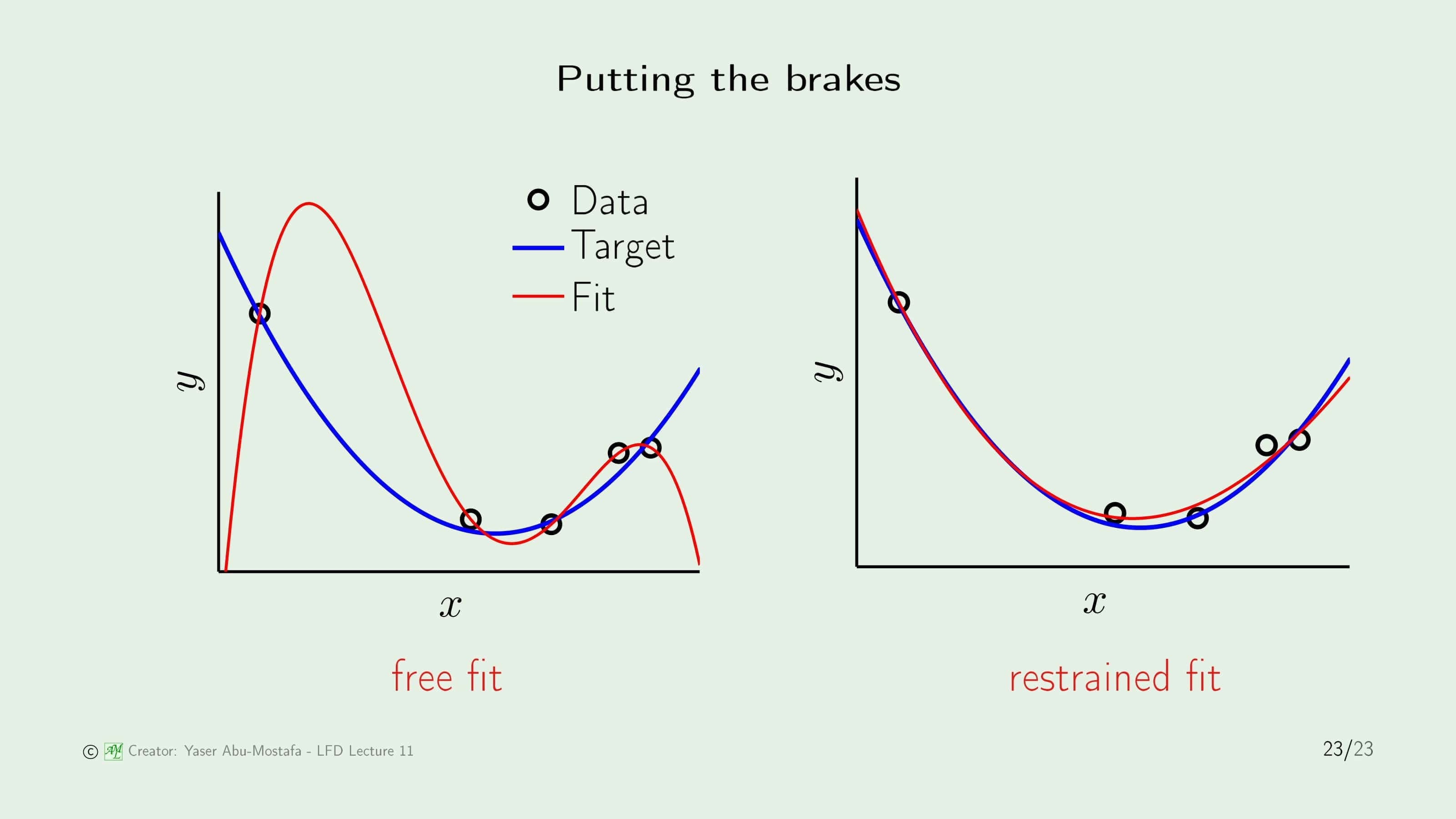
다음 장에서 바로 Regulatization을 배우게 될 텐데, 대충 어떤 것인지 감을 잡기 위해 이번 장의 첫 예제를 다시 한번 보여드리겠습니다. 왼쪽 그림이 바로 Overfitting의 문제를 알게 된 그 그림인데, 이 때는 모델을 4차함수로 잡았기 때문에 Target Function과 큰 차이가 벌어졌었습니다.

그런데 4차함수의 모양은 꼭 저런 모양만 있지 않습니다. 4차함수의 변수를 약간 변형시킨다면, 오른쪽 그림과 같이 2차 함수와 비슷한 모양으로 변해 4차함수로 모델을 잡더라도 Overfitting 문제를 해결할 수 있습니다. 바로 그 방법이 무엇인지 구체적으로 배우게 될 예정입니다.

이번 장은 여기까지입니다. 읽어주셔서 감사합니다.