On-policy Prediction with Approximation

Part II : Approximate Solution Methods

2부에서는 1부에서 사용한 Tabular Method를 확장하여 매우 큰 State Space를 가진 문제에 적용합니다. 예를 들어, 카메라 이미지의 가능한 수는 우주의 원자 수보다 훨씬 많습니다. 이렇게 방대한 State Space를 가진 문제의 경우에는 시간과 데이터가 부족하기 때문에 지금까지 배운 Optimal Policy나 Optimal Value Function를 찾을 수 없습니다. 그렇기 때문에 이제부터는 제한된 계산 자원을 활용하여 정확하지 않더라도 그에 가까운 Approximate Solution을 대신 목표로 합니다.

State Space가 클 때 Tabular Method를 사용하기 힘든 이유는 Table에 필요한 메모리 뿐만 아니라 Table을 정확하게 채우는 데 필요한 시간과 데이터도 부족하기 때문입니다. State Space가 매우 큰 경우, Episode마다 마주치게 되는 대부분의 State는 처음 방문하는 State가 됩니다. 이러한 환경에서 합리적인 의사결정을 하기 위해서는 현재 방문한 State와 유사한 다른 State에서의 기록을 토대로 일반화할 필요가 있습니다. 즉, Approximate Solution의 핵심 아이디어는 일반화입니다. State Space 중 일부의 Experience만을 토대로 좋은 Approximate Solution을 찾아야 합니다.

다행스럽게도 이러한 일반화는 이미 많이 연구된 주제이며, 강화학습에 사용하기 위해 새로운 방법을 연구할 필요가 없습니다. 이번 장에서 다룰 대부분의 방법은 기존에 연구된 일반화 방법과 강화학습을 결합하는 것으로 이 문제를 해결합니다. 강화학습에서 필요한 일반화는 원하는 함수(주로 Value Function)의 표본을 토대로 전체 함수의 근사치를 구하기 위한 일반화이기 때문에, 이를 Function Approximation이라고도 합니다. Function Approximation은 Machine Learning, Neural Network, Pattern Recognition 및 Statistical Curve Fitting과 같은 Supervised Learning의 한 예입니다. 이론적으로 이 분야에서 연구된 모든 방법은 강화학습에 사용할 수 있습니다.

그러나 Function Approximation을 사용한 강화학습에는 Nonstationarity, Bootstrapping, Delayed Target과 같은 기존의 Supervised Learning에서 발생하지 않는 여러가지 새로운 문제가 포함됩니다. 이것은 앞으로 5개의 장에 걸쳐 하나씩 소개할 예정입니다. 처음에는 On-policy로만 주제를 제한하며, 9장에서는 Policy가 주어져서 그것의 Value Function으로만 근사화되는 사례를 다루고, 10장에서는 근사를 이용해 Optimal Policy를 찾을 수 있는 Control 문제를 다룹니다. 11장부터는 Off-policy로 확장하여 12장에서는 $n$-step으로 확장한 Eligibility Trace를 소개하고 분석하며, 마지막 13장에서는 Optimal Policy를 직접 근사하고 Value Function을 근사할 필요가 없는 Control 방법인 Policy Gradient에 대해 다룰 예정입니다.

이번 장에서는 먼저 On-policy 데이터에서 State-Value Function을 먼저 추정합니다. 주어진 Policy $\pi$를 사용하여 생성된 Experience에서 $v_{\pi}$를 근사하기 위해, 강화학습에서의 Function Approximation에 대해 설명합니다. 핵심적인 내용은 Approximate Value Function이 기존과 같은 Tabular가 아니라 Weight Vector $\mathbf{w} \in \mathbb{R}^d$를 매개변수로 갖는 함수로 표현된다는 것입니다. 이에 대한 표현으로, 주어진 Weight Vector $\mathbf{w}$와 주어진 State $s$에 대해, $\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s)$를 사용합니다. Approximate Value Function $\hat{v}$를 구하는 방법에는 수많은 종류가 있으며, 이번 장에서 그 중 몇 가지를 살펴볼 예정입니다. 또한 Weight Vector $\mathbf{w}$ 원소의 수(즉, $\mathbf{w}$의 차원)는 State의 갯수보다 훨씬 적으며, 하나의 Weight를 변경해도 수많은 State의 Prediction Value가 변경됩니다. 또한 단 하나의 State가 Update되어도 이 변경 사항은 일반화되기 때문에 다른 State의 Value에도 영향을 주게 됩니다. 이러한 일반화는 학습을 강력하게 만들기도 하지만, 이렇게 관리하기 어렵게 만들기도 합니다.

Function Approximation을 사용한 강화학습은 Agent가 부분적으로만 관찰할 수 있는 일부 State에도 적용할 수 있습니다. Value Function 자체가 매개변수화된 함수로 추정되기 때문에, State, 또는 State-Action 쌍이 입력되기만 한다면 그로부터 해당 Value가 계산되는 방식이기 때문입니다. 이것과 관련한 내용은 이 장보다 Section 17.3에서 간단하게 다룰 예정입니다.

Value-function Approximation

지금까지 이 책에서 다루었던 모든 Prediction 방법은 특정 State의 Value를 해당 State에 대한 Backed-up Value 또는 Update Target으로 표현하였습니다. 이제 각각의 개별 Update를 $s \mapsto u$로 표기하는데, $s$는 Updated State이고, $u$는 $s$의 Estimated Value가 이동하는 Update Target입니다. 예를 들어, Value Prediction을 위한 Monte Carlo Update는 $S_t \mapsto G_t$, TD(0) Update는 $S_t \mapsto R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}_t)$, 그리고 $n$-step TD Update는 $S_t \mapsto G_{t:t+n}$으로 표기할 수 있습니다. Dynamic Programming의 Policy Evaluation Update는 $s \mapsto \mathbb{E}_{\pi} \left[ R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}_t) \mid S_t = s \right]$로, 임의의 State $s$가 Update되지만, 다른 경우에는 Real Experience에서 발생한 State $S_t$가 Update됩니다.

이 새로운 Update 표현 $s \mapsto u$는 State $s$에 대한 Estimated Value가 Update Target $u$와 더 유사해야 함을 의미합니다. 지금까지 실제 Update는 $s$의 Estimated Value에 대한 Table 값은 $u$를 향해 약간만 이동했으며, 다른 모든 State의 Estimated Value는 변하지 않았습니다. 이제부터는 Update에서 $s$의 Estimated Value가 변하면 다른 많은 State의 Estimated Value도 변경되도록 일반화합니다. 이렇게 입력-출력과 예시를 사용하여 모방하는 기계학습을 Supervised Learning이라고 하며, 출력이 $u$와 같은 숫자라면 이 과정을 Function Approximation이라고 합니다. Function Approximation화 방법은 근사하려는 함수의 입력-출력 예제를 통해 학습하며, Function Approximation가 완료되었을 때의 그 함수를 Estimated Value Function이라고 해석합니다.

강화학습에서 Value Function Prediction을 위해 Function Approximation을 사용할 때, 원칙적으로는 Artificial Neural Network, Decision Tree 및 다양한 종류의 Multivariate Regression을 포함한 모든 Supervised Learning 방법을 사용할 수 있습니다. 그러나 모든 Function Approximation 방법이 강화학습에 적합한 것은 아닙니다. 강화학습에서는 Agent가 Environment, 또는 Environment Model과 상호작용하는 동안 학습이 온라인으로 수행되는 것이 중요하기 때문입니다. 이를 위해서는 점진적으로 얻어진 데이터를 효율적으로 학습할 수 있는 방법이 필요합니다. 또한 강화학습은 일반적으로 Nonstationary Target Function을 처리할 수 있는 Function Approximation 방법이 필요합니다. (즉, 시간이 지남에 따라 변경되는 Target Function) 예를 들어, Generalized Policy Iteration (GPI)에 기반한 Control에서 종종 $\pi$가 변경되는 동안 $q_{\pi}$를 학습하였습니다. Policy가 동일하게 유지되더라도 Dynamic Programming이나 Temporal-Difference Learning에서의 Bootstrapping 방법은 Target Value가 Nonstationary였습니다. 그렇기 때문에 Nonstationary 특성을 제대로 처리할 수 없는 방법은 강화학습에 적합하지 않습니다.

The Prediction Objective ($\overline{\text{VE}}$)

지금까지는 Prediction에 대한 명시적인 목표를 정하지 않았습니다. Tabular의 경우에는 학습된 Value Function이 Real Value Function과 정확히 같아질 수 있기 때문에 Prediction에 대한 성능 평가가 필요하지 않았습니다. 게다가 각각의 State에 대한 Update는 다른 State에 전혀 영향을 끼치지 않았습니다. 하지만 이제부터 다룰 근사적인 방법은 한 State의 Update가 다른 State에 영향을 미치는데다, 모든 State의 Value를 정확하게 구할 수도 없습니다. 왜냐하면 가정에 의해, Weight보다 훨씬 더 많은 State를 가지고 있으므로 한 State의 Estimated Value를 더 정확하게 만드는 행위는 항상 다른 State의 Estimated Value를 덜 정확하게 만들기 때문입니다. 따라서 어떤 State에 집중할 것인지 먼저 논의해보아야 합니다. State $s$에 대한 Error를 얼마나 중요하게 생각하는지 측정하기 위해, State Distribution $\mu(s) \ge 0, \sum_s \mu(s) = 1$을 정의합니다. 또한 State $s$에 대한 Error는 $\hat{v}(s, \mathbf{w})$와 $v_{\pi}(s)$ 차이의 제곱을 의미합니다. 이를 State Space에 대해 $\mu$만큼 Weight를 부여하면, Mean Square Value Error $\overline{\text{VE}}$는 다음과 같이 표현할 수 있습니다.

\[\overline{\text{VE}}(\mathbf{w}) \doteq \sum_{s \in \mathcal{S}} \mu(s) \left[ v_{\pi}(s) - \hat{v}(s, \mathbf{w}) \right]^2 \tag{9.1}\]

식 (9.1)에 제곱근을 씌운 값은 근사한 Value Function이 Real Value Function과 얼마나 차이가 나는지를 대략적으로 측정하는데 사용됩니다. $\mu(s)$는 종종 State $s$에서 보낸 시간의 일부로 사용합니다. On-policy에서 이것은 On-policy Distribution이라고 하는데, 이번 장에서는 여기에 초점을 맞출 계획입니다. Continuing Task에서 On-policy Distribution은 $\pi$ 하에서의 Stationary Distribution입니다.

The On-policy Distribution in Episodic Tasks

Episodic Task에서 On-policy Distribution은 Episode의 초기 State가 선택되는 방식에 따라 다릅니다. 한 Episode가 State $s$에서 시작될 확률을 $h(s)$라고 하고, 단일 Episode에서 State $s$에 소요된 평균 시간 단계 수를 $\eta(s)$라고 정의하면, Episode가 State $s$에서 시작하거나 이전 State $\bar{s}$에서부터 전이되었을 때 State $s$에 머문 시간은 다음과 같습니다.

\[\eta(s) = h(s) + \sum_{\bar{s}} \eta(\bar{s}) \sum_a \pi (a|\bar{s}) p(s|\bar{s}, a), \quad \text{for all } s \in \mathcal{S} \tag{9.2}\]

이 식은 $\eta(s)$에 대해서도 풀 수 있습니다. On-policy Distribution은 다음과 같이 합이 1로 Normalize된 각 State에서 소요된 시간의 비율입니다.

\[\mu(s) = \frac{\eta(s)}{\sum_{s'} \eta(s')}, \quad \text{for all } s \in \mathcal{S} \tag{9.3}\]

이것은 Discounting을 고려하지 않은 경우입니다. 만약 Discounting ($\gamma < 1$)이 있는 경우에는 간단하게 식 (9.2)의 두 번째 항에 $\gamma$를 추가함으로써 해결할 수 있습니다.

□

Continuing Task와 Episodic Task는 비슷하게 동작하지만, 엄밀하게 따지면 두 경우를 별개로 구분하여 각각 분석해야 합니다.

다만 $\overline{\text{VE}}$가 강화학습에서 올바른 성능 평가의 목표인지는 명확하지 않습니다. Value Function을 학습하는 궁극적인 목적은 더 나은 Policy를 찾는 것인데, 이 목적을 위한 Optimal Value Function이 반드시 $\overline{\text{VE}}$를 최소화하지는 않기 때문입니다. 하지만 그럼에도 불구하고 $\overline{\text{VE}}$보다 더 나은 성능 평가의 척도가 없기 때문에 여기서는 $\overline{\text{VE}}$에 초점을 맞추도록 하겠습니다.

$\overline{\text{VE}}$의 관점에서 이상적인 목표는 모든 $\mathbf{w}$에 대해 $\overline{\text{VE}}(\mathbf{w}^{*}) \le \overline{\text{VE}}(\mathbf{w})$인 Global Optimum을 찾는 것입니다. 이것을 찾는 것은 Linear Approximation과 같은 간단한 Function Approximation에서는 가능하지만, Neural Network나 Decision Tree와 같은 복잡한 Function Approximation에서는 거의 불가능합니다. 따라서 복잡한 Function Approximation에서는 $\mathbf{w}^{*}$의 주변 $\mathbf{w}$에 대해 $\overline{\text{VE}}(\mathbf{w}^{*}) \le \overline{\text{VE}}(\mathbf{w})$를 만족하는 Local Optimum에 대신 수렴하게 만듭니다. 이정도가 non-Linear Approximation에서 할 수 있는 최대한이지만, 불행하게도 많은 경우에 그조차도 수렴한다는 보장이 없습니다. 몇몇 방법은 실제로 $\overline{\text{VE}}$가 무한대로 발산하기도 합니다.

지금까지 두 Section에 걸쳐 Value Function의 Prediction을 위해 광범위한 강화학습 방법을 Function Approximation 방법과 결합하기 위한 아이디어를 설명했으며, 강화학습의 Update를 사용하여 Function Approximation을 위한 데이터를 생성했습니다. 또, Optimal Value Function Prediction을 위해 성능 평가의 척도인 $\overline{\text{VE}}$를 제안했습니다. Function Approximation 방법은 그 종류가 너무 많기 때문에 여기서 모두 고려할 수는 없고, 일단 여기에서는 Gradient에 기반한 방법, 특히 Linear Gradient Descent 방법에 중점을 두도록 하겠습니다.

Stochastic-gradient and Semi-gradient Methods

이번 Section에서는 Stochastic Gradient Descent (SGD)를 기반으로 하는 Value Function Prediction 방법을 자세히 소개합니다. SGD는 모든 Function Approximation 방법 중 가장 널리 사용되는 방법 중 하나이며, 온라인 강화학습에 적합한 특징을 갖고 있습니다. Gradient Descent와 Stochastic Gradient Descent는 아래 포스트에도 소개되어 있으니 참고해주시면 좋겠습니다.

• [기계학습] 9. Linear Model II

Gradient Descent에서 Weight Vector $\mathbf{w} \doteq (w_1, w_2, \ldots, w_d)^{\sf T}$는 고정된 실수 값 요소를 갖는 Column Vector이고, $\hat{v}(s, \mathbf{w})$는 모든 State $s \in \mathcal{S}$에 대해 $\mathbf{w}$로 미분가능한 함수입니다. 이산적인 시간 단계 $t = 0, 1, 2, 3, \ldots$에 대한 Weight Vector $\mathbf{w}$의 값을 $\mathbf{w}_t$로 표기합니다. 또한 State $S_t$로부터 주어진 Policy에 따른 Real Value를 $S_t \mapsto v_{\pi} (S_t)$와 같이 정확하게 얻는다고 가정하겠습니다.

먼저 식 (9.1)과 같이 $\overline{\text{VE}}$를 최소화하려는 것과 동일한 Distribution $\mu$를 가진 상황에서 State를 방문한다고 가정하겠습니다. 이 경우 가장 좋은 방법은 관찰된 데이터에서 오류를 최소화하는 것입니다. SGD는 각 데이터를 입력받은 후, 아래와 같이 해당 데이터의 오류를 줄이는 방향으로 Weight Vector $\mathbf{w}$를 조절합니다.

\[\begin{align} \mathbf{w}_{t+1} &\doteq \mathbf{w}_t - \frac{1}{2} \alpha \nabla \left[ v_{\pi}(S_t) - \hat{v}(S_t, \mathbf{w}_t) \right]^2 \tag{9.4} \\ \\ &= \mathbf{w}_t + \alpha \left[ v_{\pi}(S_t) - \hat{v} (S_t, \mathbf{w}_t) \right] \nabla \hat{v}(S_t, \mathbf{w}_t) \tag{9.5} \end{align}\]

식 (9.4), (9.5)에서 $\alpha$는 Step-size Parameter이고, $\nabla f(\mathbf{w})$는 다음과 같이 Scalar 표현식인 $f(\mathbf{w})$를 Vector $\mathbf{w}$에 대해 편미분한 식입니다.

\[\nabla f(\mathbf{w}) \doteq \left( \frac{\partial f(\mathbf{w})}{\partial w_1}, \frac{\partial f(\mathbf{w})}{\partial w_2}, \cdots, \frac{\partial f(\mathbf{w})}{\partial w_d} \right)^{\sf T} \tag{9.6}\]

식 (9.6)의 미분 Vector는 $\mathbf{w}$에 대한 $f$의 Gradient입니다. SGD는 Update가 완료될 때 Stochastic이라고 하는데, 왜냐하면 확률적으로 선택된 단일 데이터(Sample)에 대해 Update하기 때문입니다. 많은 데이터에 대해 작은 단계를 수행한다면, 전체적인 효과는 $\overline{\text{VE}}$를 최소화하는 것과 같습니다.

SGD를 포함한 Gradient Descent에서 Update 시 기울기 방향으로 작은 단계만을 이동하는데, 이것은 여러 데이터의 오류에 대한 균형을 맞추기 위함입니다. 극단적으로 데이터 하나가 들어올 때 그 데이터에서 오류가 0인 지점으로 (즉, 크게) 이동하면 해당 데이터에 대해 최소한의 오류만 가질 수 있으나, 그만큼 다른 데이터들에 대해 오류가 커지게 됩니다. 모든 State에 대해 오류가 0인 Value Function를 찾는 것은 목표도 아닐 뿐더러 목표로 할 수도 없습니다. 이 Step-size Parameter $\alpha$는 시간에 따라 감소하여 식 (2.7)의 조건을 충족시키도록 설계합니다. 이 조건을 만족하면 식 (9.5)의 SGD는 Local Optimum에 수렴합니다.

이제 $t$번째 학습 데이터인 $S_t \mapsto U_t \in \mathbb{R}$을 따져보겠습니다. $U_t$는 $S_t$의 Real Value인 $v_{\pi}(S_t)$가 아니라 근사값입니다. 예를 들면 $U_t$는 $v_{\pi}(S_t)$에 노이즈가 추가된 버전일 수도 있고 $\hat{v}$를 사용하는 Bootstrapping 버전일 수도 있으며, 심지어는 경우에 따라 무작위 값일 수도 있습니다. 이런 경우에는 $v_{\pi}(S_t)$ 값을 알 수 없기 때문에 식 (9.5)를 수행할 수 없지만, $v_{\pi}(S_t)$ 대신 $U_t$를 사용하여 근사할 수도 있습니다. 이것은 State Value를 추정하기 위해 다음과 같은 일반적인 SGD 방법을 의미합니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ U_t - \hat{v}(S_t, \mathbf{w}_t) \right] \nabla \hat{v} (S_t, \mathbf{w}_t) \tag{9.7}\]

만약 $U_t$가 Bias되지 않은 추정값인 경우(즉, $\mathbb{E} \left[ U_t \mid S_t = s \right] = v_{\pi} (s)$인 경우) 각각의 $t$에 대해 $\mathbf{w}_t$는 식 (2.7)과 같은 조건을 만족한다면 Local Optimum에 수렴하는 것이 보장됩니다. 예를 들어, Policy $\pi$에 따라 Environment(또는 Simulated Environment)와 상호작용에 의해 생성된 State를 가정하면, State의 Real Value $v_{\pi}$는 그 State 이후의 Reward에 대한 기대값이기 때문에 Monte Carlo의 Target인 $U_t \doteq G_t$는 그 정의에 의해 $v_{\pi}(S_t)$의 Bias되지 않은 추정값입니다. 이것을 사용한 식 (9.7)의 일반적인 SGD는 Local Optimum에 수렴하는 것이 보장됩니다. 따라서 Monte Carlo의 State Value 추정은 Gradient Descent을 통해 Local Optimum에 수렴하는 해법을 보장할 수 있습니다. Monte Carlo 버전에 대한 전체 Pseudocode는 다음과 같습니다.

하나 유의해야할 것은 $v_{\pi}(S_t)$의 Bootstrapping 추정이 식 (9.7)에서 Target $U_t$로 사용되는 경우, 동일한 수렴 보장을 얻을 수 없습니다. Bootstrapping의 Target은 $n$-step의 Return $G_{t:t+n}$ 또는 DP의 Target인 $\sum_{a, s’, r} \pi (a \mid S_t) p(s’,r, \mid S_t, a)\left[ r + \gamma \hat{v}(s’, \mathbf{w}_t \right]$처럼 Weight Vector $\mathbf{w}_t$의 현재 값에 의존하며, 이로 인해 Bias가 발생하고 Gradient Descent을 제대로 사용할 수 없습니다. 다행히 식 (9.4)와 (9.5)까지의 핵심 단계는 Target이 $\mathbf{w}_t$에 독립적입니다. 실제로 Bootstrapping 방법은 진정한 Gradient Descent의 인스턴스가 아니라고 밝혀졌으며(Barnard, 1993), Bootstrapping은 Estimated Value가 Weight Vector $\mathbf{w}_t$에는 영향을 끼치지만 Target에 대한 영향은 무시합니다. 즉, Gradient의 일부만 포함하기 때문에 Bootstrapping을 Semi-Gradient Method라고 부릅니다.

Semi-Gradient(=Bootstrapping) 방법은 Gradient 방법만큼 강력하게 수렴하지 않지만, 다음 Section에서 다룰 Linear 방법과 같은 특정한 경우에는 안정적으로 수렴합니다. 또한 어떤 경우에는 Semi-Gradient 방법의 장점이 유용한 경우도 있습니다. 대표적인 Semi-Gradient의 장점은 일반적으로 다른 방법보다 학습 속도가 빠르다는 것과 Episode가 끝날 때까지 기다릴 필요 없이 온라인으로 학습이 가능하다는 것입니다. 따라서 Continuing Task 같은 문제에 사용할 수 있는 이점이 있습니다. 기본적인 Semi-Gradient 방법은 $U_t \doteq R_{t+1} + \gamma \hat{v} (S_{t+1}, \mathbf{w})$를 Target으로 하는 Semi-Gradient TD(0)입니다. 이것의 완전한 Pseudocode는 다음과 같습니다.

State Aggregation은 각 그룹에 대해 하나의 Estimated Value(Weight Vector $\mathbf{w}$의 한 구성 요소)를 사용하여 State를 그룹화함으로써 Function Approximation을 일반화하는 간단한 형태입니다. State의 Value는 해당 그룹의 구성 요소로 추정되며, State가 Update되면 해당 구성 요소만 Update됩니다. State Aggregation은 Gradient $\nabla \hat{v} (S_t, \mathbf{w}_t)$가 State $S_t$ 그룹의 구성 요소에 대해 1이고 다른 구성 요소에 대해 0인 SGD (식 9.7)의 특별한 경우입니다.

Linear Methods

Function Approximation의 가장 중요하고 특별한 경우 중 하나는 Approximate Function $\hat{v}(\cdot, \mathbf{w})$가 Weight Vector $\mathbf{w}$에 대해 Linear인 경우입니다. Linear Method는 모든 State $s$에 대해 $\mathbf{w}$와 동일한 차원인 Real-valued Vector $\mathbf{x}(s) \doteq (x_1(s), x_2(s), \cdots, x_d(s))^{\sf T}$가 있으며, 다음과 같이 $\mathbf{w}$와 $\mathbf{x}(s)$ 사이의 내적으로 State의 Value를 근사화하는 방법입니다.

\[\hat{v} (s, \mathbf{w}) \doteq \mathbf{w}^{\sf T} \mathbf{x}(s) \doteq \sum_{i=1}^d w_i x_i (s) \tag{9.8}\]

식 (9.8)과 같이 추정한 Value Function를 Linear in the Weights, 또는 단순히 Linear라고 부릅니다.

Vector $\mathbf{x}(s)$는 State $s$를 표현하는 Feature Vector라고 부릅니다. Vector $\mathbf{x}(s)$의 각 구성 요소인 $x_i (s)$는 함수 $x_i : \mathcal{S} \to \mathbb{R}$의 값입니다. 여기서는 Feature를 이러한 함수들의 전체 집단으로 간주하고, State에 대한 Value를 $s$에 대한 Feature라고 부릅니다. Linear Method에서 Feature는 Approximate Function들의 집합에 대한 Linear Basis를 형성하기 때문에 Basis Function입니다. State를 나타내기 위해 $d$차원 Feature Vector를 구성하는 것은 $d$ Basis Function의 집합을 선택하는 것과 동일합니다. Feature는 다양한 방법으로 정의될 수 있는데, 이는 다음 Section에서 자세히 다루도록 하겠습니다.

다시 Function Approximation로 돌아와서, Linear Function의 근사를 SGD Update와 사용할 경우, Weight Vector $\mathbf{w}$에 대한 Approximate Value Function의 Gradient는 다음과 같습니다.

\[\nabla \hat{v}(s, \mathbf{w}) = \mathbf{x}(s)\]

Linear의 경우 일반 SGD Update 식 (9.7)은 다음과 같이 간단하게 수정할 수 있습니다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \left[ U_t - \hat{v} (S_t, \mathbf{w}_t) \right] \mathbf{x}(S_t)\]

Linear SGD는 매우 간단하기 때문에 수학적으로 분석하기 쉽습니다. 대부분의 학습 방법에서 유용한 수렴 결과는 거의 Linear나 그보다 간단한 Function Approximation 방법에 대한 것입니다. 특히 Linear의 경우 Optimum이 하나만 있기 때문에 Local Optimum에 수렴하는 것이 보장되기만 하면 Global Optimum, 또는 그 근처에 수렴하는 것이 보장됩니다. 예를 들어, 이전 Section에서 다룬 Gradient Monte Carlo 알고리즘은 $\alpha$가 시간이 지남에 따라 감소하는 일반적인 조건을 만족할 시 Linear Function Approximation에서 $\overline{\text{VE}}$의 Global Optimum에 수렴합니다.

또한 Semi-Gradient TD(0) 알고리즘은 Linear Function Approximation에서도 수렴하지만, SGD의 일반적인 결과를 따르지 않기 때문에 별도의 Theorem이 필요합니다. 수렴되는 Weight Vector $\mathbf{w}$ 또한 Global Optimum이 아니라 Local Optimum에 가까운 지점이기 때문입니다. 특히 Continuing Task와 같은 특별한 경우를 고려해보면, 각 시간 $t$에서의 Update는 다음과 같습니다.

\[\begin{align} \mathbf{w}_{t+1} &\doteq \mathbf{w}_t + \alpha \left( R_{t+1} + \gamma \mathbf{w}_t^{\sf T} \mathbf{x}_{t+1} - \mathbf{w}_t^{\sf T} \mathbf{x}_t \right) \mathbf{x}_t \tag{9.9} \\ \\ &= \mathbf{w}_t + \alpha \left( R_{t+1} \mathbf{x}_t - \mathbf{x}_t \left( \mathbf{x}_t - \gamma \mathbf{x}_{t+1} \right)^{\sf T} \mathbf{w}_t \right) \end{align}\]

식 (9.9)에서는 $\mathbf{x}_t = \mathbf{x}(S_t)$와 같이 표기를 간소화하여 사용했습니다. 시스템이 Steady State에 도달하면, 주어진 $\mathbf{w}_t$에 대해 예상되는 다음 Weight Vector를 다음과 같이 표현할 수 있습니다.

\[\mathbb{E} \left[ \mathbf{w}_{t+1} | \mathbf{w}_t \right] = \mathbf{w}_t + \alpha \left( \mathbf{b} - \mathbf{A} \mathbf{w}_t \right) \tag{9.10}\]

식 (9.10)에서 $\mathbf{b}$와 $\mathbf{A}$는 다음과 같습니다.

\[\mathbf{b} \doteq \mathbb{E} \left[ R_{t+1} \mathbf{x}_t \right] \in \mathbb{R}^d \quad \text{and} \quad \mathbf{A} \doteq \mathbb{E} \left[ \mathbf{x}_t \left( \mathbf{x}_t - \gamma \mathbf{x}_{t+1} \right)^{\sf T} \right] \in \mathbb{R}^{d \times d} \tag{9.11}\]

식 (9.10)에서 시스템이 수렴하는 경우, Weight Vector $\mathbf{w}_{\text{TD}}$로 수렴해야 합니다. 즉,

\[\begin{align} \mathbf{b} - \mathbf{A} \mathbf{w}_{\text{TD}} &= \mathbf{0} \\ \\ \mathbf{b} &= \mathbf{A} \mathbf{w}_{\text{TD}} \\ \\ \mathbf{w}_{\text{TD}} &\doteq \mathbf{A}^{-1} \mathbf{b} \tag{9.12} \\ \\ \end{align}\]

식 (9.12)와 같은 결과를 TD Fixed Point라고 합니다. 실제로 Linear Semi-Gradient TD(0)는 TD Fixed Point로 수렴합니다. 이 수렴성과 역행렬 $\mathbf{A}^{-1}$의 존재에 대한 증명은 다음과 같습니다.

Proof of Convergence of Linear TD(0)

식 (9.9)의 수렴을 보장하는 속성을 찾기 위해, 먼저 식 (9.10)을 다음과 같이 변형해보겠습니다.

\[\mathbb{E} \left[ \mathbf{w}_{t+1} | \mathbf{w}_t \right] = \left( \mathbf{I} - \alpha \mathbf{A} \right) \mathbf{w}_t + \alpha \mathbf{b} \tag{9.13}\]

식 (9.13)에서 행렬 $\mathbf{A}$는 Weight Vector $\mathbf{w}_t$를 곱하지만 $\mathbf{b}$는 곱하지 않습니다. 즉, 수렴하기 위해서는 $\mathbf{A}$만 중요합니다. 먼저, 행렬 $\mathbf{A}$가 Diagonal Matrix인 경우를 고려해보겠습니다. 만약 대각선 원소(=$A_{ij}$에서 $i = j$인 원소) 중에 하나라도 음수가 된다면 $\mathbf{I} - \alpha \mathbf{A}$의 대각선 원소가 1보다 커지고, 이로 인해 $\mathbf{w}_t$의 요소가 증폭되기 때문에 발산이 일어납니다. 반면에 $\mathbf{A}$의 대각선 원소가 모두 양수라면 $\alpha$는 가장 큰 원소보다 작게 선택될 수 있으므로, $\mathbf{I} - \alpha \mathbf{A}$는 0과 1 사이의 모든 대각선 원소가 있는 Diagonal Matrix입니다. 이 경우에는 Update 식의 첫 번째 항이 $\mathbf{w}_t$를 작게 만들기 때문에 안정적입니다. 일반적으로는 $\mathbf{A}$가 Positive Definite (=$y^{\sf T} \mathbf{A} y > 0$)일 때 $\mathbf{w}_t$가 0으로 감소합니다. 또한 Positive Definite 특성이 있다면 $\mathbf{A}$의 역행렬 $\mathbf{A}^{-1}$의 존재가 보장됩니다.

Linear TD(0)의 경우 Continuing Task에서 $\gamma < 1$이라면 식 (9.11)의 행렬 $\mathbf{A}$는 다음과 같이 정리할 수 있습니다.

\[\begin{align} \mathbf{A} &= \sum_s \mu (s) \sum_a \pi (a|s) \sum_{r, s'} p (r, s' | s, a) \mathbf{x}(s) \left( \mathbf{x}(s) - \gamma \mathbf{x}(s') \right)^{\sf T} \\ \\ &= \sum_s \mu (s) \sum_{s'} p (s'|s) \mathbf{x}(s) \left( \mathbf{x}(s) = \gamma \mathbf{x}(s') \right)^{\sf T} \\ \\ &= \sum_s \mu (s) \mathbf{x}(s) \left( \mathbf{x}(s) - \gamma \sum_{s'} p(s'|s) \mathbf{x}(s') \right)^{\sf T} \\ \\ &= \mathbf{X}^{\sf  T} \mathbf{D} (\mathbf{I} - \gamma \mathbf{P}) \mathbf{X} \end{align}\]

여기서 $\mu (s)$는 Policy $\pi$의 Stationary Distribution, $p(s’ \mid s)$는 Policy $\pi$에서 State $s$로부터 State $s’$으로의 Transition Probability, $\mathbf{P}$는 Transition Probability를 나타낸 행렬 $\lvert \mathcal{S} \rvert \times \lvert \mathcal{S} \rvert$, $\mathbf{D}$는 $\mu (s)$가 대각선 원소로 있는 Diagonal Matrix $\lvert \mathcal{S} \rvert \times \lvert \mathcal{S} \rvert$, 그리고 $\mathbf{X}$는 $\mathbf{x}(s)$가 행으로 있는 행렬 $\lvert \mathcal{S} \rvert \times d$ 입니다. 여기에 내부 행렬 $\mathbf{D} (\mathbf{I} - \gamma \mathbf{P})$는 행렬 $\mathbf{A}$의 Positive Definite 성질을 보장하는 핵심 부분입니다.

이 핵심 행렬 $\mathbf{D} (\mathbf{I} - \gamma \mathbf{P})$은 모든 Column의 합계가 음수가 아니라면, Positive Definite가 보장됩니다. (Sutton, 1988) $\mathbf{D} (\mathbf{I} - \gamma \mathbf{P})$에서 대각선 원소는 양수이고, 그 외의 원소는 음수이므로 각 Row 합과 Column의 합이 양수라는 것을 보여야 합니다. $\mathbf{P}$가 Stochastic Matrix이고, $\gamma < 1$이므로 Row의 합은 모두 양수입니다. 행렬 $\mathbf{1}$을 모든 원소가 1인 Column Vector라고 할 때, 임의의 행렬 $\mathbf{M}$에 대해 Column의 합은 $\mathbf{1}^{\sf T} \mathbf{M}$으로 표현할 수 있습니다. $\boldsymbol{\mu}$를 $\mu (s)$의 $\mathcal{S}$-Vector라고 하면 $\boldsymbol{\mu} = \mathbf{P}^{\sf T} \boldsymbol{\mu}$가 성립하는데, $\mu$가 Stationary Distribution이기 때문입니다. 핵심 행렬의 Column 합은 다음과 같습니다.

\[\begin{align} \mathbf{1}^{\sf T} \mathbf{D} (\mathbf{I} - \gamma \mathbf{P}) &= \boldsymbol{\mu}^{\sf T} - \gamma \boldsymbol{\mu}^{\sf T} \mathbf{P} \\ \\ &=\boldsymbol{\mu}^{\sf T} - \gamma \boldsymbol{\mu}^{\sf T} \mathbf{P} \\ \\ &=\boldsymbol{\mu}^{\sf T} - \gamma \boldsymbol{\mu}^{\sf T} \quad \text{(} \because \text{ } \boldsymbol{\mu} \text{ is the stationary distribution)} \\ \\ &= (1 - \gamma) \boldsymbol{\mu}^{\sf T} \end{align}\]

즉, 모든 구성 요소가 양수입니다. 따라서 이 핵심 행렬과 $\mathbf{A}$는 Positive Definite이며, On-policy TD(0)는 안정적입니다. 다만 Linear TD(0)가 확률 1로 수렴하는 것을 증명하기 위해서는 시간이 지남에 따라 $\alpha$가 작아진다는 것을 포함한 추가적인 조건들이 필요합니다. 여기서 그 부분은 생략하도록 하겠습니다.

□

TD Fixed Point에서 Continuing Task라면 $\overline{\text{VE}}$가 다음과 같이 가능한 가장 낮은 Error에 Bound하다는 것이 증명되었습니다.

\[\overline{\text{VE}}(\mathbf{w}_{\text{TD}}) \le \frac{1}{1 - \gamma} \min_{\mathbf{w}} \overline{\text{VE}}(\mathbf{w}) \tag{9.14}\]

이것이 보여주는 것은 TD의 Asymptotic Error가 Monte Carlo Method에서 얻은 가능한 가장 작은 Error의 $\frac{1}{1 - \gamma}$배 이하라는 것입니다. $\gamma$는 종종 1에 가깝기 때문에 $\overline{\text{VE}}(\mathbf{w})$가 상당히 클 수 있으므로, TD의 경우 Asymptotic 성능이 상당히 저하될 가능성이 있습니다. 하지만 6장과 7장에서 배우듯, TD는 Monte Carlo Method에 비해 Variance가 크게 낮고 빠르기 때문에 각각의 장단점이 있습니다. 어떤 방법이 더 좋은지는 근사값과 문제의 환경, 그리고 학습이 얼마나 오래 지속되는지에 따라 다릅니다.

식 (9.14)와 비슷한 Bound는 다른 On-policy Bootstrapping 방법에도 적용됩니다. 예를 들어, On-policy Distribution에 따라 Update된 식 (9.7)의 Linear Semi-Gradient DP 또한 TD Fixed Point로 수렴합니다. 다음 장에서 다룰 Semi-Gradient Sarsa(0)와 같은 1-step Semi-Gradient Action-Value 방법은 비슷한 Fixed Point와 Bound로 수렴합니다. Episodic Task의 경우에는 약간 다르지만 유사한 Bound가 있습니다. (Bertsekas and Tsitsiklis, 1996) Reward, Feature, 그리고 Step-size Parameter의 감소에 대한 여러 가지 기술적인 조건들도 있지만, 여기에서는 생략하겠습니다. 이것에 대한 자세한 내용은 (Tsitsiklis and Van Roy, 1997)의 논문에서 찾을 수 있습니다.

지금까지 설명한 수렴 결과에 중요한 점은 On-policy Distribution에 따라 State가 Update된다는 것입니다. 다른 Distribution에 따른 Update의 경우 Function Approximation를 사용하는 Bootstrapping은 무한대로 발산할 수 있기 때문입니다. 이에 대한 예와 가능한 해결 방법은 11장에서 다룰 예정입니다.

물론 지금까지 배운 내용을 1-step TD(0)에서만 사용할 수 있는 것은 아닙니다. 7장에서 배운 Tabular $n$-step TD 알고리즘을 Semi-Gradient Function Approximation로 확장한 Semi-Gradient $n$-step TD 알고리즘의 전체 Pseudocode는 다음과 같습니다.

위의 알고리즘에서의 가장 중요한 식은 다음과 같이 식 (7.2)와 유사합니다. ($0 \le t < T$)

\[\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1} + \alpha \left[ G_{t:t+n} - \hat{v}(S_t, \mathbf{w}_{t+n-1}) \right] \nabla \hat{v}(S_t, \mathbf{w}_{t+n-1}) \tag{9.15}\]

이 때 $n$-step Return $G_{t:t+n}$은 다음과 같이 변형됩니다. ($0 \le t \le T - n$)

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1} R_{t+n} + \gamma^n \hat{v} (S_{t+n}, \mathbf{w}_{t+n-1}) \tag{9.16}\]

Feature Construction for Linear Methods

이전 Section에서 배운대로 Linear Method는 수렴을 보장하는 이점이 있습니다. 하지만 그 외에도 데이터 처리나 계산이 매우 효율적일 수 있다는 장점도 있습니다. ~일 수 있다라고 표현한 것처럼 모든 Linear Method가 그렇다는 것은 아니기 때문에 이번 Section에서는 다양한 Linear Feature를 하나하나 살펴보며 어떤 장점이 있는지, 그리고 강화학습에 얼마나 적합한지를 살펴보겠습니다.

Linear 구조의 한계는 각각의 Feature에 대해 상호작용을 고려할 수 없다는 것입니다. 예를 들어, Pole-Balancing 문제에서 높은 Angular Velocity는 Angle에 따라 좋을 수도 있고 나쁠 수도 있습니다. Angle이 높은 상황에서 Angular Velocity가 높다면 Pole이 낙하할 위험이 크다는 것을 의미하고(나쁜 State), Angle이 낮은 상황에서 Angular Velocity가 높다면 Pole이 옳은 방향으로 가고 있음을 의미합니다(좋은 State). Linear 구조에서 이렇게 Feature 간에 상호작용을 고려하기 위해서는 추가적인 구현이 필요합니다. 이어지는 하위 Section에서는 이를 위한 다양한 방법을 소개합니다.

Polynomials

많은 문제들에서 State는 Pole-Balancing 문제에서의 위치와 속도처럼 숫자로 표시됩니다. 이런 유형의 문제에서의 강화학습을 위한 Function Approximation는 Interpolation 및 Regression 작업과 많은 공통점이 있기 때문에, Interpolation 및 Regression에서 사용되는 Feature들 또한 강화학습에 사용할 수 있습니다. Polynomial은 Interpolation 및 Regression에서 사용되는 가장 단순한 Feature 중 하나로써, 간단하고 친숙하기 때문에 가장 먼저 소개합니다. 하지만 그 단순함 때문에 이후에 소개될 Feature들에 비해 성능은 좋다고 볼 수 없습니다.

Polynomial Feature를 이해하기 쉽게 예를 들어 설명해보겠습니다. 임의의 강화학습 문제에서 두 개의 숫자 차원이 있는 State가 있다고 가정합니다. 이 강화학습에서 State $s$는 두 숫자 $s_1 \in \mathbb{R}$, $s_2 \in \mathbb{R}$로 이루어져 있으며, 이를 Feature Vector로 표현하면 $\mathbf{x}(s) = (s_1, s_2)^{\sf T}$로 나타낼 수 있습니다. 하지만 이렇게 표현하는 경우 두 개의 차원 간 상호작용을 고려할 수 없다는 것과, $s_1$과 $s_2$가 모두 0이라면 근사값도 0이어야 한다는 문제가 있습니다. 이를 해결하는 간단한 방법은 State의 Feature Vector $\mathbf{x}(s)$를 4차원으로 늘려 $\mathbf{x}(s) = (1, s_1, s_2, s_1 s_2)^{\sf T}$로 만드는 방법이 있습니다. 첫 차원의 1은 원래 State의 숫자를 Affine Function으로 표현할 수 있고, 마지막 차원의 $s_1 s_2$을 사용하면 $s_1$과 $s_2$의 상호작용을 고려할 수 있습니다. 더 복잡한 상호작용을 고려하고 싶다면 Feature Vector의 차원을 더욱 늘려 $\mathbf{x}(s) = (1, s_1, s_2, s_1 s_2, s_1^2, s_2^2, s_1 s_2^2, s_1^2 s_2, s_1^2 s_2^2)^{\sf T}$와 같이 표현할 수도 있습니다. 이러한 Feature Vector는 복잡해보이지만, Weight에 기반한 Linear Approximation은 임의의 이차함수로 근사가 가능합니다. 이 예시를 일반화한다면 $k$개의 차원 간의 매우 복잡한 상호작용도 표현할 수 있습니다.

Polynomial Feature 상호작용의 일반화

각각의 State $s$가 $s_i \in \mathbb{R}$인 $k$개의 숫자 $s_1$, $s_2$, $\ldots$, $s_k$로 이루어져있다고 가정한다. 이 $k$개 차원의 State Space에 대해, $n$차 Polynomial Basis Feature $x_i$는 다음과 같이 표현할 수 있다.

\[x_i = \prod_{j=1}^k s_j^{c_{i, j}} \tag{9.17}\]

이 때 $c_{i, j} \in \{ 0, 1, \ldots, n \}$이며(단, $n \ge 0$인 정수), 이 Feature는 $(n + 1)^k$개의 서로 다른 Feature를 포함하는 $k$ 차원에 대해 $n$차 Polynomial Basis를 구성한다.

□

고차 Polynomial Base를 사용하면 더 복잡한 함수를 더 정확하게 근사할 수 있습니다. 그러나 $n$차 Polynomial Basis의 Feature 수는 차원 $k$에 따라 기하급수적으로 증가하기 때문에 일반적으로 Function Approximation를 위해서는 이것들의 부분 집합을 선택해야 합니다. 이것은 근사화할 함수에 대한 Prior Belief로 수행할 수 있으며, Polynomial Regression를 위해 개발된 여러 선택 방법을 적용하여 강화학습의 Incremental 및 Nonstationary 특성을 처리할 수 있습니다.

Fourier Basis

또 다른 Linear Function Approximation은 Fourier Series에 기반하여 만들 수 있습니다. Fourier Series는 서로 다른 Frequency를 가진 Sine 및 Cosine Basis Feature의 Weighted Sum으로 표현합니다. Fourier Series와 Fourier Transform은 Approximate Function가 알려진 경우 Basis Function의 Weight는 간단한 식으로 표현되며, Basis Function이 충분하면 기본적으로 모든 함수를 정확하게 근사할 수 있습니다. 강화학습에서 Approximate Function은 알려지지 않았기 때문에 Fourier Basis Function은 사용하기 쉽고, 다양한 강화학습 문제에서 잘 사용할 수 있습니다.

먼저 1차원 환경을 고려해보겠습니다. $\tau$의 Period를 갖는 1차원 함수에서 일반적인 Fourier Series 표현은 Period를 $\tau$로 나눈 Sine과 Cosine 함수의 Linear 조합으로 나타납니다. 그러나 만약 Bounded Interval에서 정의된 Aperiodic Function을 근사하기 위해서는 $\tau$를 구간의 길이로 설정하여 Fourier Basis Function을 사용할 수 있습니다. 그렇게 되면 Aperiodic Function은 Sine 및 Cosine Feature의 Periodic Linear 조합의 한 Period가 됩니다.

또한 $\tau$를 구간 길이의 2배로 설정하고, 구간의 절반인 $\left[ 0, \tau / 2 \right]$에서 근사값을 제한하면 Cosine Feature만 사용할 수 있습니다. Cosine Feature만 사용한다면 $y$축에 대칭인 Even Function으로 나타낼 수 있습니다. 따라서 Half-Period $\left[ 0, \tau / 2 \right]$에 대한 모든 함수는 Cosine Feature를 사용하여 근사할 수 있습니다. 마찬가지로 Sine Feature만을 사용하면 원점에 대해 대칭인 Odd Function을 만들 수 있습니다. 그러나 Half-Even Function이 Half-Odd Function보다 근사하기 쉽기 때문에 일반적으로 Cosine Feature만 사용하는 것이 좋습니다. 특히 Half-Odd Function은 종종 원점에서 불연속이기 때문입니다. 물론 일부 특정 상황에서는 Sine 및 Cosine Feature를 모두 사용할 수도 있습니다.

이러한 논리에 따라 $\tau = 2$로 설정하고 Feature는 $\tau$의 Half-Interval $\left[ 0, 1 \right]$에서 정의되도록 하면, 1차원 $n$차 Fourier Cosine Basis는 다음과 같은 $n + 1$ Feature로 표현됩니다.

\[x_i (s) = \cos (i \pi s), \quad s \in \left[ 0, 1 \right], \quad i = 0, \ldots n\]

아래의 그림은 $i = 1, 2, 3, 4$인 경우 1차원 Fourier Cosine Feature $x_i$를 나타냅니다. (단, $x_0$은 상수 함수입니다.)

이를 확장하여 Fourier Cosine Series를 다차원으로 일반화한 근사는 다음과 같습니다.

Fourier Cosine Series의 일반화

각각의 State $s$가 $s_i \in \left[ 0, 1\right]$인 $k$개의 숫자로 이루어진 Vector $\mathbf{s} = (s_1, s_2, \ldots, s_k)^{\sf T}$로 이루어져있다고 가정한다. $n$차 Fourier Cosine Basis의 $i$번째 Feature는 다음과 같이 표현할 수 있다.

\[x_i (s) = \cos (\pi \mathbf{s}^{\sf T} \mathbf{c}^i) \tag{9.18}\]

식 (9.18)에서 $\mathbf{c}^i = (c_1^i, \ldots, c_k^i)^{\sf T}$는 $j = 1, \ldots, k$와 $i = 1, \ldots, (n+1)^k$에 대해 $c_j^i \in \{ 0, \ldots, n \}$로 이루어져 있다. 이것은 $(n+1)^k$개의 가능한 정수 Vector $\mathbf{c}^i$에 대한 각각의 Feature를 정의한다. Vector $\mathbf{s}^{\sf T}$와 $\mathbf{c}^i$의 Inner Product $\mathbf{s}^{\sf T} \mathbf{c}^i$는 정수 $\{ 0, \ldots, n \}$를 $\mathbf{s}$의 각 차원에 할당하는 효과를 갖는다. 1차원의 경우 이 정수값은 해당 차원에서 Feature의 Frequency를 결정한다. 물론 이 Feature는 응용 프로그램에 따라 제한된 State Space에 맞게 이동 및 확장될 수 있다.

□

예를 들어 $\mathbf{s} = (s_1, s_2)^{\sf T}$인 경우를 고려해보겠습니다. (즉, $k = 2$) 여기서 $\mathbf{c}^i = (c_1^i, c_2^i)^{\sf T}$입니다. 아래의 그림은 6개의 Fourier Cosine Feature를 선택하여 보여줍니다. 각각의 그림은 이를 정의하는 Vector $\mathbf{c}^i$에 따라 어떻게 표현되는지 나타나 있습니다. $\mathbf{c}$에서 0이 의미하는 것은 해당 State가 차원에 따라 Feature가 일정함을 의미합니다. 따라서 만약 $\mathbf{c} = (0, 0)^{\sf T}$라면 Feature는 두 차원 모두 일정하다는 뜻입니다. 만약 $\mathbf{c} = (c_1, 0)^{\sf T}$이라면 Feature는 첫 번째 차원에서는 $c_1$에 따라 Frequency가 변하지만 두 번째 차원에서 일정합니다. 당연히 $\mathbf{c} = (0, c_2)^{\sf T}$라면 그 반대가 됩니다. 만약 $\mathbf{c} = (c_1, c_2)^{\sf T}$라면 Feature가 두 차원에 따라 달라지며 두 State 변수 간의 상호작용을 나타냅니다. $c_1$과 $c_2$의 값은 각 차원에 따른 Frequency를 결정하고 이들의 비율은 상호작용의 방향을 나타냅니다.

Fourier Cosine Feature를 사용할 때 식 (9.7)과 같은 학습 알고리즘을 사용한다면 각 Feature에 대해 다른 Step-size Parameter를 사용하는 것이 좋을 수도 있습니다. 만약 $\alpha$가 기본 Step-size Parameter라면 Feature $x_i$에 대해 Step-size Parameter $\alpha_i$를 $\alpha / \sqrt{(c_1^i)^2 + \cdots + (c_k^i)^2}$로 설정할 수도 있습니다. (Konidaris, Osentoski and Thomas, 2011) 단, $c_j^i = 0$인 경우는 $\alpha_i = \alpha$로 설정합니다.

Sarsa의 Fourier Cosine Feature는 앞서 설명한 Polynomial이나 뒤에 나올 Radial Basis Function을 비슷한 여러 Basis에 비해 우수한 성능을 보일 수 있습니다. 그러나 Fourier Feature는 매우 높은 Frequency Basis Function이 포함되어 있지 않는 한, 불연속 지점 주변에서 Ringing을 피하기 어렵기 때문에 불연속성에서 문제가 있습니다.

$n$차 Fourier Basis의 Feature 수는 State Space의 차원에 따라 기하급수적으로 증가하지만, 해당 차원이 작은 경우라면(ex. $k \le 5$) 모든 $n$차 Fourier Feature를 사용할 수 있도록 $n$을 선택할 수 있습니다. 하지만 고차원 State Space의 경우에는 이러한 Feature의 하위 집합을 선택해야 합니다. Polynomial 때와 마찬가지로 근사화할 함수에 대한 Prior Belief를 사용하여 선택할 수 있으며, 몇몇 자동화된 선택 방법을 사용하여 강화학습의 Incremental 및 Nonstationary 특성을 처리할 수 있습니다. 이 때 Fourier Basis Feature의 장점은 $\mathbf{c}^i$ Vector를 설정하여 State 변수 간의 상호작용을 처리하고 근사 함수가 소음으로 간주될 수 있는 높은 Frequency 성분들을 걸러낼 수 있도록 $\mathbf{c}^i$ Vector의 값을 제한함으로써 Feature를 쉽게 선택할 수 있습니다. 반면에 Fourier Feature는 Global Property를 나타내는 전체 State Space에서 0이 아니기 때문에 Local Property를 나타내는 좋은 방법을 찾기 어려울 수 있습니다.

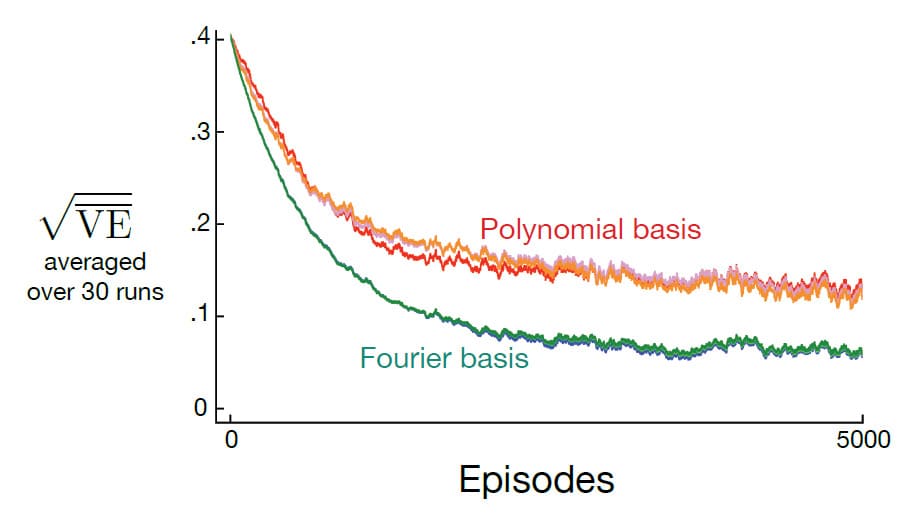
아래의 그림은 1000개의 State를 가진 Random Walk 예제에서 Fourier와 Polynomial의 Basis를 비교하는 학습 곡선을 나타냅니다. 보시다시피 Fourier Basis의 성능이 월등히 좋기 때문에 일반적인 온라인 학습에는 Polynomial을 사용하지 않는 것이 좋습니다.

Coarse Coding

State 집합을 연속적인 2차원 공간에 표현하는 상황을 고려해보겠습니다. 이 경우 표현할 수 있는 방법 중 하나는 아래 그림처럼 State Space에 원과 같은 모양의 Feature를 생각해볼 수 있습니다. State가 원 안에 있으면 해당 Feature의 값은 1이고, 이 때 Present한다고 합니다. 반대로 그렇지 않다면 Feature의 값은 0이고, 이 때는 Absent라고 합니다. 이렇게 1-0으로 표현하는 Feature를 Binary Feature라고 합니다. 주어진 State에서 어떤 Binary Feature가 있는지는 해당 State가 속한 원을 나타냅니다. 이러한 방식으로 겹치는 Feature가 있는 State를 나타내는 것을 Coarse Coding이라고 합니다. 다만 꼭 아래 그림처럼 원 모양일 필요는 없습니다.

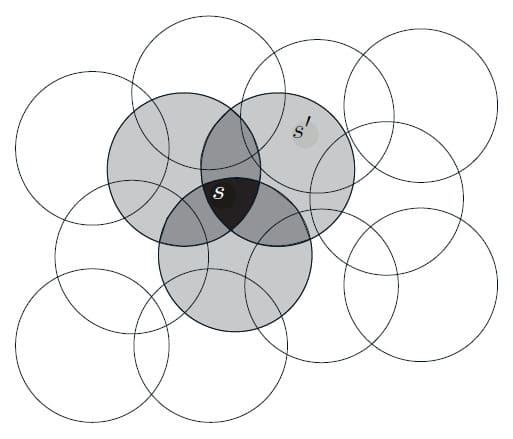
Linear Gradient Descent을 사용한 근사라고 가정하면, 원의 크기와 밀도가 어떤 영향을 끼치는지 고려해봐야 합니다. 각각의 원은 학습에 의해 영향을 받는 단일 Weight(즉, $\mathbf{w}$의 구성 요소)입니다. State Space의 한 State에서 훈련을 하면, 해당 State를 포함하는 모든 원의 Weight가 영향을 받습니다. 따라서 식 (9.8)에 의해 근사 Value Function는 원의 합집합 내의 모든 State에 영향을 미치며, 한 점이 많은 State에 속해 있을수록 더 큰 영향을 미칩니다.

위의 그림은 Coarse Coding의 여러 일반화 형태를 나타내고 있습니다. 왼쪽의 그림처럼 원의 작다면 일반화가 보다 좁은 영역에서 이루어지며, 중간의 그림처럼 원이 크다면 일반화가 보다 넓은 영역에서 이루어집니다. 게다가 Feature의 형태는 일반화의 특성에도 영향을 미칩니다. 오른쪽의 그림처럼 좁은 타원 형태라면 일반화도 그에 맞춰 영향을 받게 됩니다.

큰 Receptive Field가 있는 Feature는 광범위한 일반화를 제공하지만, 학습된 Feature를 대략적인 근사로 제한하기 때문에 일반화가 너무 대략적으로 나오는 것처럼 보일 수 있습니다. 초기 일반화는 실제로 Receptive Field의 크기와 모양에 의해 결정되지만, 궁극적인 추정 결과의 정확도는 전체 Feature 수에 의해 더 많이 영향을 받습니다. 이것은 다음 예제를 통해 자세하게 설명하겠습니다.

Example 9.3) Coarseness of Coarse Coding

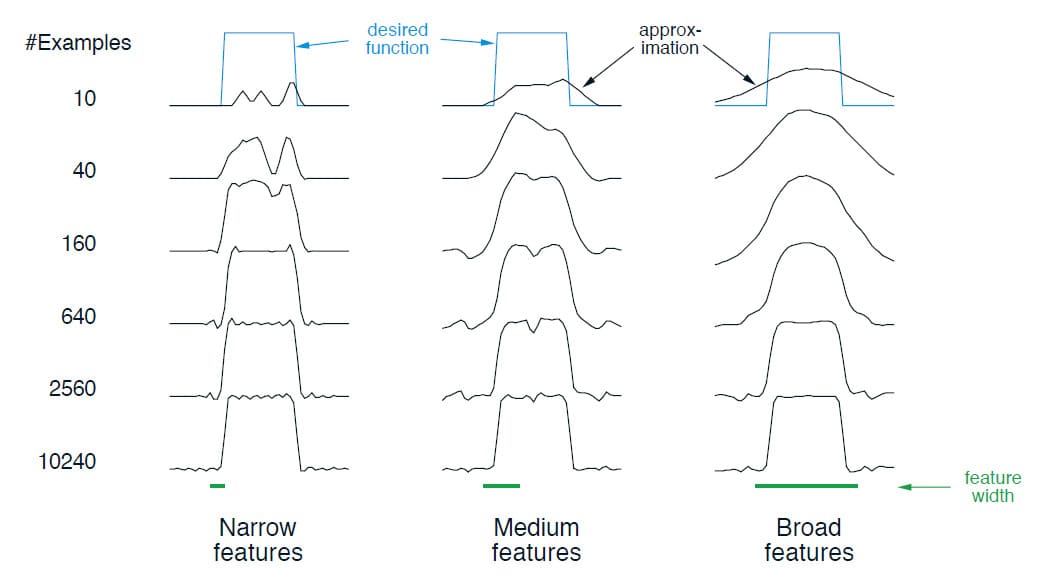
이 예제는 Coarse Coding에서 Receptive Field의 크기에 따른 학습 효과를 보여줍니다. Coarse Coding 및 식 (9.7)에 기반한 Linear Function Approximation는 1차원 Square-wave 함수를 학습하는 데 사용되었습니다. 이 함수의 Target은 $U_t$로 설정되었고, 단 하나의 차원에서 Receptive Field는 원 대신 Interval이었습니다. 학습은 아래 그림과 같이 세 가지 다른 길이의 너비(Narrow, Medium, Broad)로 반복되었습니다. 또한 세 가지 모두 학습되는 Feature의 범위에 대해 약 50개의 동일한 Density를 가졌습니다. Training Data(Sample)는 이 범위에서 무작위로 균일하게 생성되었습니다. Step-size Parameter는 한 번에 존재했던 Feature의 수를 $n$이라 할 때 $\alpha = \frac{0.2}{n}$으로 설정되었습니다. 아래의 그림은 세 가지 경우에서 각각 학습했을 때의 Feature를 나타냅니다. 보시다시피 Feature의 너비는 학습 초기에 큰 영향을 끼칩니다. 하지만 최종 결과를 보시면 Feature의 너비에 그다지 큰 영향을 끼치지 않는 것을 알 수 있습니다.

□

Tile Coding

Tile Coding은 Coarse Coding의 한 형태로써 다차원 연속 공간에서 유연하고 계산이 효율적인 특징을 가지고 있습니다. 교재에서는 이 방법을 현대 Sequential 디지털 컴퓨터에서 가장 실용적인 Feature라고 주장하고 있습니다.

Tile Coding에서 Feature의 Receptive Field는 State Space의 Partition으로 그룹화됩니다. 이러한 각 Partition을 Tiling이라고 하며, Partition의 각 요소를 Tile이라고 합니다. 예를 들어, 2차원 State Space의 가장 단순한 Tiling은 아래 그림의 왼쪽에 나타난 것과 같이 균일한 격자입니다. 여기에서 Tile(=Receptive Field)은 사각형입니다. 이 단일 Tiling만 사용할 경우, 흰색 점으로 표시된 State는 Tile이 속하는 단일 Feature로 표현됩니다. 일반화는 동일한 Tile 내의 모든 State에 대해 완전하고, Tile 외부 State에는 존재하지 않습니다. 하나의 Tiling인 경우 Coarse Coding 보다는 State Aggregation에 가깝습니다.

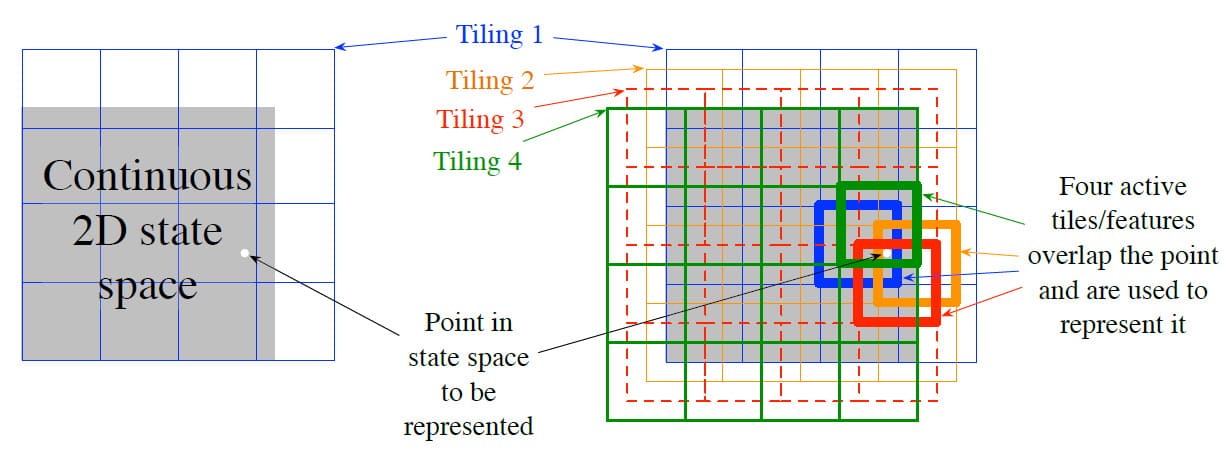
Coarse Coding의 장점을 얻으려면 겹치는 Receptive Field가 필요한데, Tile Coding의 정의상 Partition의 Tile은 겹치지 않습니다. 이를 해결하기 위해서는 여러 Tiling을 사용하며, 각 Tiling은 Tile 너비의 일부로 설정합니다. 위 그림의 오른쪽은 4개의 Tiling을 사용한 경우입니다. 흰색 점으로 표시된 것과 같이 모든 State는 4개의 Tiling 각각에서 정확히 하나의 Tile에 속합니다. 이 4개의 Tile은 State에 도달할 때 활성화되는 4개의 Feature에 해당합니다. 특히, Feature Vector $\mathbf{x}(s)$는 각 Tiling에서 각각의 Tile에 대해 하나의 구성 요소를 갖습니다. 예를 들어, 위의 그림에서는 $4 \times 4 \times 4 = 64$개의 구성 요소가 있습니다. 이 중 State $s$가 속하는 Tile 4개를 제외하고는 모두 0의 값이 됩니다.

Tile Coding의 실제 장점은 Partition과 함께 작동하기 때문에 한 번에 활성화되는 전체 Feature 수가 모든 State에서 동일하다는 것입니다. 각 Tiling에는 정확히 하나의 Feature가 있으므로 존재하는 Feature의 총 수는 항상 Tiling 수와 동일합니다. 이것으로 인해 Step-size Parameter $\alpha$를 쉽고 직관적인 방식으로 설정할 수 있습니다. 예를 들어 Tiling 수를 $n$이라 할 때, $\alpha = \frac{1}{n}$로 설정하면 정확히 1회 학습이 됩니다. 이 때 만약 데이터 $s \to v$가 학습된 경우, 이전 Estimated Value $\hat{v} (s, \mathbf{w}_t)$가 무엇이든 상관없이 새로운 Estimated Value는 $\hat{v} (s, \mathbf{w}_t) = v$가 됩니다. 다만 일반적으로 Target Output의 일반화나 Stochastic Variation을 위해 이보다 더 천천히 변경하는 것을 선호하기 때문에, $\alpha = \frac{1}{10n}$로 선택한다면 한 번의 Update로 Target 까지 $\frac{1}{10}$만큼 이동하고, 인접한 State는 Tile 수에 비례하여 덜 이동합니다.

Tile Coding은 또한 Binary Feature Vector를 사용하여 계산상의 이점을 얻습니다. 각각의 구성 요소가 0 또는 1이므로 식 (9.8)과 같은 Approximate Value Function에서 Weighted Sum을 계산하기 매우 쉽기 때문입니다. 식 (9.8)에서 곱셈 연산을 수행할 필요 없이, 구성 요소가 1인 항목들만 전부 더하면 끝입니다.

일반화는 학습이 끝난 State가 아닌 다른 State가 공통된 Tile 수에 비례하여 동일한 Tile에 속하는 경우에 발생합니다. Tiling을 서로 Offset하는 방법의 선택조차도 일반화에 영향을 줍니다. 만약 Tiling의 Offset이 각 차원마다 균일하게 설정되어 있으면, 아래 그림의 위쪽과 같이 다른 State는 다른 방식으로 일반화됩니다. 위쪽의 8개의 그림은 각각 학습된 State에서 가까운 지점으로 일반화한 패턴을 보여줍니다. 이 예시에서는 8개의 Tiling이 있으므로 Tile 내 64개의 하위 영역이 명확하게 일반화되고, 모두 이 8개의 패턴 중 하나에 따릅니다. 문제는 Tiling이 균일할 때 대각선 요소의 영향력이 매우 강하다는 것입니다. (ex. 6번째와 8번째 그림의 비교) 만약 아래쪽 그림처럼 Tiling의 Offset이 비대칭적으로 설정되면 이러한 효과를 피할 수 있습니다. 이것이 바로 비대징 Offset이 Tile Coding에서 선호되는 이유입니다.

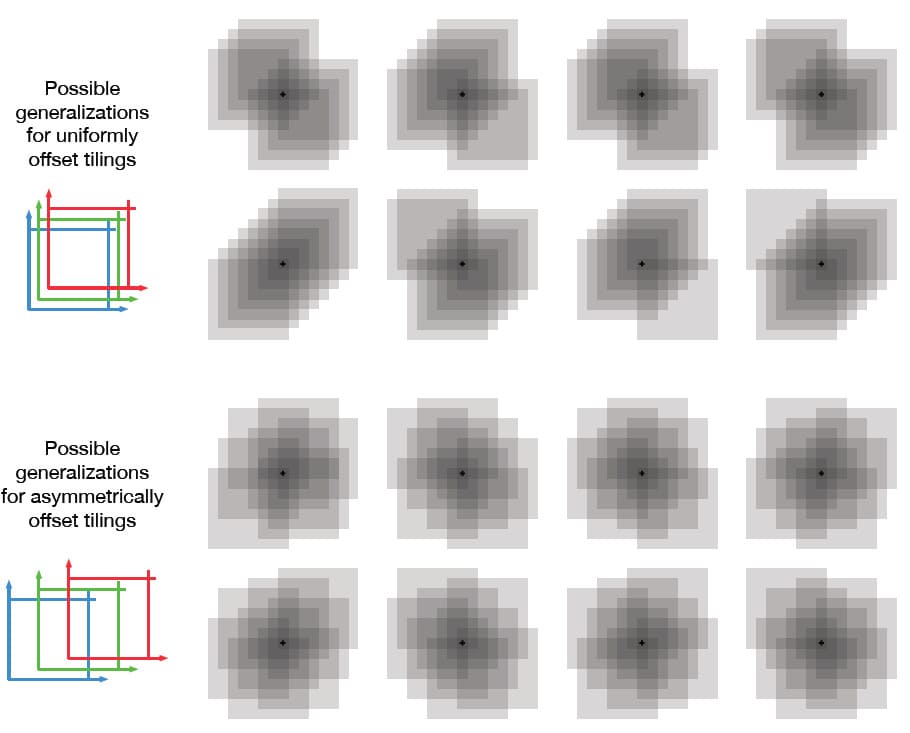
모든 경우에서 Tiling은 각 차원의 Tile 너비 일부만큼 서로 Offset이 설정됩니다. Tile의 너비를 $w$라 하고 Tile의 수를 $n$으로 한다면 $\frac{w}{n}$이 기본 단위입니다. 작은 사각형 $\frac{w}{n}$ 안의 모든 State들은 같은 Tile이 활성화되고, 같은 Feature와 같은 근사값을 같습니다. State가 아무 방향으로 $\frac{w}{n}$ 만큼 이동하면 Feature가 하나의 구성 요소/Tile 만큼 변경됩니다. 균일하게 Offset이 설정된 Tiling은 정확히 이 단위 거리만큼 Offset이 설정됩니다. 2차원 공간에서 각 Tiling은 Displacement Vector에 의해 Offset이 설정되며, 이는 Tiling의 Offset이 이 Vector에서 $\frac{w}{n}$ 를 곱한 만큼 설정된다는 의미입니다. 예를 들어, 위의 그림 중 아래쪽(Tiling이 비대칭인 경우)은 Displacement Vector (1, 3)에 의해 Offset 됩니다. Tile Coding의 일반화에서 다양한 Displacement Vector의 영향은 많은 연구가 이루어졌고, 교재에도 이에 대한 설명이 나와있으나, 여기에서는 생략하도록 하겠습니다.

Tiling을 설계한다는 것은 Tiling의 수와 Tile의 모양을 선택하는 것과 같습니다. Tiling의 수는 Tile의 크기와 함께 Asymptotic Approximation의 Resolution과 Fineness를 결정합니다. 또한 Tile의 모양은 일반화에 대한 특징을 결정합니다. (Coarse Coding 부분 참고) 예를 들어, 위에서 다룬 정사각형 모양의 Tile은 각각의 차원에서 거의 동일하게 일반화됩니다. 아래 그림은 Tile의 다양한 모양을 나타내고 있습니다. 가운데의 수직 줄무늬 모양 Tile은 왼쪽에서 더 촘촘하고 얇게 디자인되어 있기 때문에 수평 차원을 기준으로 낮은 값일 수록 촘촘한 분류가 가능합니다. 오른쪽 그림의 대각선 줄무늬 Tiling은 보는 바와 같이 대각선을 따라 일반화를 합니다. 왼쪽과 같은 불규칙한 Tiling도 가능하지만, 실제로 많이 쓰는 방법은 아닙니다.

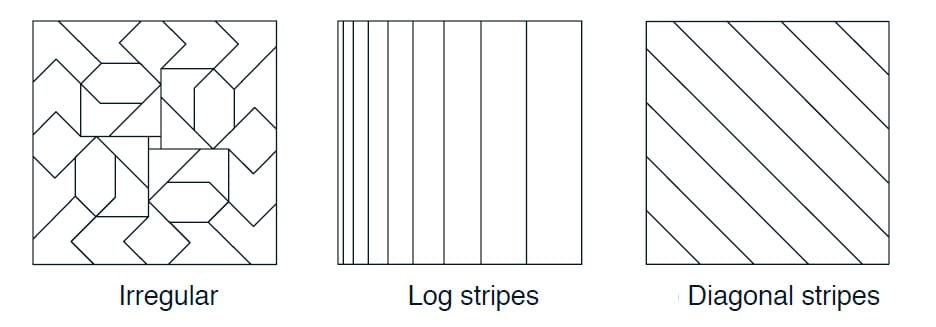
실제로 Tiling을 설계할 때는 다른 Tiling에 다른 모양의 Tile을 사용하는 것이 좋습니다. 예를 들어, 한 Tiling은 수직 줄무늬, 다른 Tiling은 수평 줄무늬를 사용하는 방법이 있습니다. 이것은 어느 차원에서든 일반화를 가능케 하지만, 줄무늬 모양의 Tiling 만으로는 수평 및 수직 좌표의 특정 조합이 고유한 값을 갖는다는 것을 학습할 수 없습니다. 이를 위해서는 직사각형 모양의 Tile이 필요합니다. 여러 Tiling을 조합하여 사용하면 이런 문제를 해결할 수 있습니다. 보통은 각 차원을 따라 일반화하는 것을 선호하지만, 조합에 따른 특정한 값을 학습하기 위해서는 별도의 방법이 필요합니다. (Sutton, 1996) Tiling의 선택은 일반화를 결정하며, 이 선택이 효과적으로 자동화될 수 있을 때까지 유연하고 사람들이 이해할 수 있는 방식으로 선택할 수 있는 것이 중요합니다.

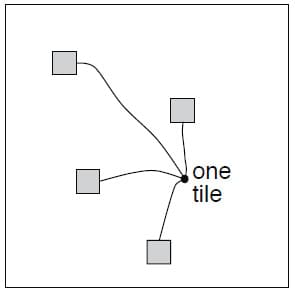
Tile Coding에서 메모리 요구 사항을 줄이는 유용한 트릭 중 하나는 Hashing입니다. 이것은 큰 Tile을 훨씬 더 작은 Tile의 집합으로 규칙있게 축소하는 것입니다. Hashing은 State Space 전체에 무작위로 퍼진 비연속적이고 분리된 영역으로 구성된 Tile을 생성하지만, 완전한 Partition을 형성합니다. 예를 들어, 위의 그림과 같이 하나의 Tile은 4개의 하위 Tile로 구성될 수 있습니다. Hashing은 성능 손실이 거의 없이 메모리 요구 사항을 크게 낮출 수 있는 경우가 많습니다. 이것은 State Space의 작은 부분만 높은 Resolution이 필요하기 때문입니다. 이는 어느정도 Curse of Dimensionality를 극복할 수 있다는 점에서 큰 의미가 있습니다. 보통 Tile Coding을 구현한 오픈 소스 프로그램들은 효율적인 Hashing을 적용하는 경우가 많습니다.

Radial Basis Functions

Radial Basis Function (RBF)은 연속된 값들의 Feature에 대한 Coarse Coding의 일반화입니다. 각각의 Featrue가 0 또는 1이었던 이전과 다르게 RBF는 폐구간 $\left[ 0, 1 \right]$에 있는 어떤 값이라도 될 수 있으며, Feature가 존재하는 것에 대한 Degree를 반영합니다. 일반적인 RBF Feature $x_i$는 State $s$가 Feature의 Prototypical(또는 간단하게 중앙 State) $c_i$로부터 얼마나 떨어져 있는지 Feature의 상대적인 너비 $\sigma_i$에 의존하는 Gaussian $x_i(s)$입니다. 이는 수식으로 표현하면 다음과 같은 Gaussian(=Normal) Distribution과 비슷합니다.

\[x_i (s) \doteq \exp \left( - \frac{|| s - c_i ||^2}{2 \sigma_i^2} \right)\]

물론 Norm이나 거리를 측정하는 Metric은 주어진 State나 Action에 따라 적절하게 선택할 수 있습니다. 아래 그림은 1차원 공간에서 Euclidean Distance Metric의 예를 나타냅니다.

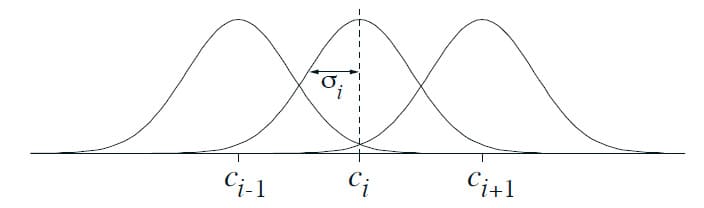
0과 1로만 값을 설정하던 Binary Featrue가 가지고 있지 않은 RBF의 주요 장점은 미분 가능한 근사 함수를 만든다는 것입니다. 사실 이것이 대부분 큰 의미는 없습니다. 다만 이것이 꽤 매력적인지 생각보다 많은 연구가 이루어졌으나 (An, 1991; Miller et al., 1991; An et al., 1991; Lane, Handelman and Gelfand, 1992) 대부분 Tile Coding에 비해 상당히 많은 추가적인 계산이 필요한데다 State 차원이 2개 이상인 경우 성능이 저하되는 경우가 많습니다. 특히 Tile의 가장자리는 높은 차원일수록 더 중요한데, RBF는 Tile의 가장자리가 잘 제어되지 않는 것이 증명되었습니다.

RBF Network는 Feature에 대해 RBF를 사용하는 Linear Function Approximation입니다. 학습은 다른 Linear Function Approximation과 마찬가지로 식 (9.7)과 (9.8)로 정의됩니다. 또한 RBF Network에 대한 일부 학습 방법은 Feature의 중심과 너비를 변경하여 non-Linear Function Approximation으로도 사용할 수 있습니다. non-Linear Method는 Target Function을 훨신 더 정확하게 맞출 수 있다는 장점을 가지고 있습니다. RBF Network, 특히 non-Linear RBF Network의 단점은 더 큰 계산 복잡도 뿐만 아니라 학습하기 전의 Manual Tuning이 더 강력하고 효율적이라는 것입니다.

RBF에 대한 더 자세한 내용은 다음 포스트를 참고해주시기 바랍니다.

• [기계학습] 16. Radial Basis Function

Selecting Step-Size Parameters Manually

대부분의 SGD 방법에서는 적절한 Step-size Parameter $\alpha$를 선택해야 합니다. $\alpha$을 선택하는 규칙이 명확하게 주어져있다면 좋겠지만, 대부분의 경우 엔지니어가 직접 Manual하게 선택합니다. 알고리즘을 잘 이해하고, 설계한 의도대로 잘 동작하게 만드려면 Step-size Parameter의 역할에 대한 직관적인 감각을 키워야 합니다. 이번 Section에서는 이러한 내용을 다루도록 하겠습니다.

이전에 배운 이론적인 고려 사항들은 불행히도 거의 도움이 되지 않습니다. 2장에서 다룬 식 (2.7)과 같은 Theory of Stochastic Approximation은 Step-size의 Sequence가 수렴을 보장하기 위해 어떤 식을 만족해야 하는지에 대한 조건을 제공하지만, 이것은 학습을 너무 느리게 만드는 경향이 있습니다. Tabular 방식의 Monte Carlo Method에서 표본 평균을 생성하는 고전적인 방법인 $\alpha = 1/t$는 Temporal Difference Learning나 Nonstationary 문제, 또는 Function Approximation에서 사용하기에 적합하지 않습니다. Linear Method의 경우 최적의 행렬 Step-size를 설정하는 Recursive Least-square 방법이 있으나, 이 방법은 Section 9.8에서 다룰 LSTD와 같은 Temporal Difference Learning에 사용하기에 적합하지 않습니다. 왜냐하면 시간 복잡도 $O(d^2)$를 가지는 Step-size Parameter나 지금까지 사용했던 Step-size Parameter들에 비해 $d$배 더 많은 Parameter가 필요하기 때문입니다. 따라서 이것들은 여기서 더 이상 사용하지 않겠습니다.

Step-size Parameter를 직접 설정하는 방법에 대해 직관적인 느낌을 얻기 위해 잠시 Tabular 형식의 강화학습 방법을 다시 생각해보겠습니다. Tabular 강화학습에서 $\alpha = 1$로 설정한다면 하나의 학습 이후 Sample Error를 완전히 제거한다는 것을 알 수 있습니다. 하지만 이번 장 초반에 언급한 것과 같이 이것보다는 학습 속도가 느려야합니다. Tabular 강화학습에서 $\alpha = \frac{1}{10}$으로 설정할 경우 평균적으로 Target에 수렴하는데 대략 10개의 Experience가 필요하며, 같은 이유로 100개의 Experience에서 학습하기 위해서는 $\alpha = \frac{1}{100}$로 설정하면 된다는 것을 이해할 수 있습니다. 즉, 일반적으로 $\alpha = \frac{1}{\tau}$라면 Tabular 강화학습은 해당 State를 약 $\tau$번 Experience한 후에 수렴합니다.

일반적인 Function Approximation에서는 각각의 State가 다른 모든 State와 유사할수도, 그렇지 않을 수도 있기 때문에 State를 얼마나 Experience해야 하는가에 대한 명확한 기준이 없습니다. 다만 Linear Function Approximation에서는 대략적인 규칙이 있습니다. 동일한 Feature Vector에 대해 $\tau$번 Experience으로 학습한다고 가정했을 때, Linear SGD 방법에서 많이 쓰이는 Step-size Parameter 설정법은 다음과 같습니다. (Rule of Thumb)

\[\alpha \doteq \left( \tau \mathbb{E} \left[ \mathbf{x}^{\sf T} \mathbf{x} \right] \right)^{-1} \tag{9.19}\]

$\mathbf{x}$는 SGD에서의 Input Vector와 동일한 분포로 선택된 임의의 Feature Vector입니다. 이 방법은 Feature Vector의 길이가 크게 변하지 않는 경우에 가장 잘 작동합니다. 이상적으로 $\mathbf{x}^{\sf T} \mathbf{x}$는 상수입니다.

Nonlinear Function Approximation : Artificial Neural Networks

Artificial Neural Network (ANN)은 non-Linear Function를 근사할 때 많이 사용됩니다. ANN에 대한 자세한 이론은 아래 포스트를 참고해주시기 바랍니다. 여기서는 ANN과 강화학습 사이의 관계에 대해서만 다루도록 하겠습니다.

• [기계학습] 10. Neural Network

다음 그림은 기본적인 Feedforward ANN의 구조를 보여줍니다. 루프가 존재하지 않고, 출력이 입력에 영향을 주지도 않습니다. 그림에서는 4개의 입력이 있는 Input Layer, 2개의 출력이 있는 Output Layer, 그리고 2개의 Hidden Layer로 구성되어 있습니다.

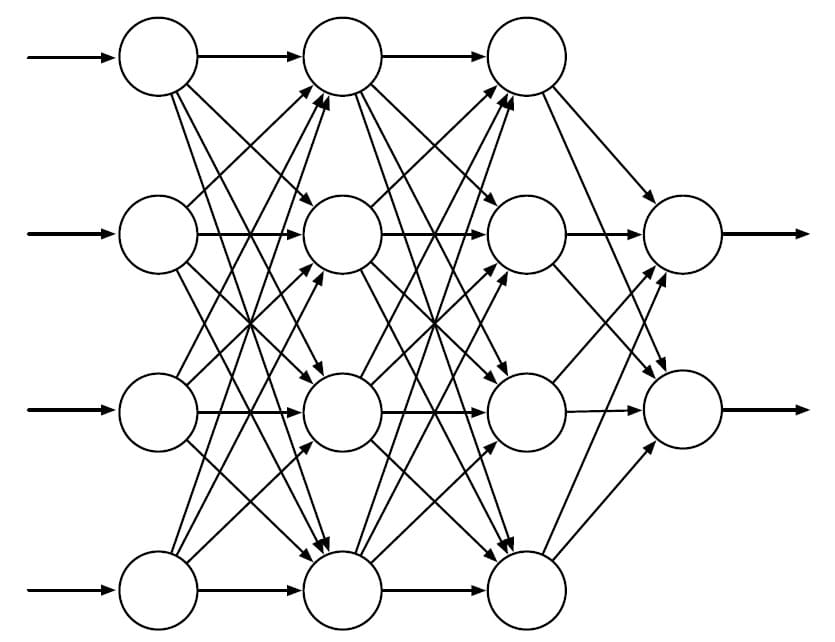
위의 그림과 같은 ANN은 원 모양의 Unit에 들어오는 입력을 Activation Function에 넣고, 그 결과를 출력하는 구조로 되어있습니다. Activation Function은 다양한 종류가 사용되는데, $f(x) = 1 / (1 + e^{-x})$와 같은 Logistic Function을 사용하는 Sigmoid Function을 사용할 수도 있고, $f(x) = \max (0, x)$와 같은 Rectifier Function이 사용될 수도 있습니다. 이 때 입력으로 들어오는 값은 그대로 들어오는 것이 아니라 해당 입력이 얼마나 중요한지에 따라 Weight가 붙습니다.

이러한 ANN의 학습 목적은 각각의 Weight에 대한 최적의 값을 결정하는 것입니다. Weight를 학습할 때 가장 많이 사용되는 알고리즘은 Backpropagation Algorithm입니다. 순방향(입력 -> 출력) 경로로 현재의 Activation Function 및 Weight를 이용하여 출력을 계산하고, 해당 입력값에 대한 정답 출력값과 비교하여 그 차이를 역방향(출력 -> 입력)으로 반영하는 것입니다. 이 과정에서 편미분이 사용되며, Weight의 값이 Update 됩니다.

Backpropagation Algorithm은 Hidden Layer가 많지 않은 ANN에서는 좋은 성능을 보이지만, Hidden Layer가 많은 경우에는 잘 작동하지 않습니다. 그 원인에는 여러가지가 있지만, 대표적으로 학습 데이터가 과도하게 반영되는 Overfitting 문제가 있으며, 이를 해결하는 방법으로 Regularization, Validation 등이 있습니다. 이에 대한 자세한 내용은 아래 포스트를 참고해주시기 바랍니다.

• [기계학습] 11. Overfitting
• [기계학습] 12. Regularization
• [기계학습] 13. Validation

이후에도 교재에서는 ANN에서 Hidden Layer가 많은 경우 생길 수 있는 문제와 그 해결 방법을 소개합니다. 다만 여기에서는 그 내용을 굳이 전부 다룰 필요는 없다고 생각하기 때문에 생략하겠습니다. 일단은 강화학습에서 Function Approximation를 할 때, ANN을 통해 non-Linear Function Model로 근사가 가능하다 정도만 이해하고 넘어가시면 될 것 같습니다. ANN과 Deep Learning에 대해서는 추후 기회가 되면 포스팅하겠습니다.

Least-Squares TD

지금까지의 Function Approximation 방법은 매개변수의 수에 비례한 시간 단계가 필요했습니다. 이번 Section에서는 다시 Linear Approximation 방법으로 돌아와서, 계산량이 조금 늘어나지만 더 나은 결과를 얻을 수 있는 Linear Approximation 방법을 소개하겠습니다.

Section 9.4에서 언급했던 것처럼, TD(0)는 식 (9.12)와 같이 Linear Function Approximation은 다음과 같은 TD Fixed Point에 수렴합니다.

\[\mathbf{w}_{\text{TD}} \doteq \mathbf{A}^{-1} \mathbf{b}\]

이 때 $\mathbf{A}$와 $\mathbf{b}$는 다음과 같습니다.

\[\mathbf{A} \doteq \mathbb{E} \left[ \mathbf{x}_t \left( \mathbf{x}_t - \gamma \mathbf{x}_{t+1} \right)^{\sf T} \right] \quad \text{and} \quad \mathbf{b} \doteq \mathbb{E} \left[ R_{t+1} \mathbf{x}_t \right]\]

Section 9.4에서 이 식을 소개했을 때는 이것을 Iterative 방법으로 계산하였습니다. 여기서 소개할 Least-Square TD (LSTD)는 이와 다르게 $\mathbf{A}$와 $\mathbf{b}$의 Estimated Value를 먼저 계산한 다음, TD Fixed Point 식을 이용하여 $\mathbf{w}_{\text{TD}}$를 직접 계산합니다. 먼저 $\mathbf{A}$와 $\mathbf{b}$의 Estimated Value을 계산하는 $\widehat{\mathbf{A}}_t$와 $\widehat{\mathbf{b}}_t$의 식부터 소개하겠습니다.

\[\widehat{\mathbf{A}}_t \doteq \sum_{k=0}^{t-1} \mathbf{x}_k \left( \mathbf{x}_k - \gamma \mathbf{x}_{k+1} \right)^{\sf T} + \varepsilon \mathbf{I} \quad \text{and} \quad \widehat{\mathbf{b}}_t \doteq \sum_{k=0}^{t-1} R_{k+1} \mathbf{x}_k \tag{9.20}\]

식 (9.20)에서 $\mathbf{I}$는 단위 행렬이고, 적당히 작은 $\varepsilon > 0$에 대해 $\widehat{\mathbf{A}}_t$는 항상 역행렬이 존재함을 보장합니다. $\widehat{\mathbf{A}}_t$와 $\widehat{\mathbf{b}}_t$의 식을 보면 이 식들을 $t$로 나누는 식이 빠져있음을 알 수 있습니다. 따라서 식 (9.20)은 사실 $\widehat{\mathbf{A}}_t$와 $\widehat{\mathbf{b}}_t$의 Estimated Value가 아니라 $\widehat{\mathbf{A}}_t \times t$와 $\widehat{\mathbf{b}}_t \times t$의 Estimated Value입니다. 하지만 아래와 같이 LSTD를 사용해서 $\mathbf{w}_t$를 계산할 때, $t$를 곱한 값은 어차피 상쇄되어 없어지기 때문에 굳이 미리 계산하지 않는 것입니다.

\[\mathbf{w}_t \doteq \widehat{\mathbf{A}}_t^{-1} \widehat{\mathbf{b}}_t \tag{9.21}\]

이 방법은 Linear TD(0)를 데이터 관점에서 가장 효율적으로 계산할 수 있는 방법이지만, 그만큼 계산 비용이 더 많이 든다는 단점도 있습니다. 이전에 Semi-gradient TD(0)는 시간 복잡도와 공간 복잡도 모두 $O(d)$만 필요했습니다. LSTD의 계산이 얼마나 복잡한지 간단하게 따져보면, $\widehat{\mathbf{A}}_t$의 Update는 Outer Product를 포함하기 때문에 시간 복잡도는 $O(d^2)$, 행렬을 저장하는데 필요한 공간 복잡도 또한 $O(d^2)$가 됩니다. 게다가 식 (9.21)을 계산하기 위해서는 $\widehat{\mathbf{A}}_t$의 역행렬을 먼저 계산해야 하는데, 이것을 계산하는데 드는 시간 복잡도가 $O(d^3)$입니다. 다행히도, $\widehat{\mathbf{A}}_t$의 역행렬을 $O(d^2)$의 시간 복잡도로 계산할 수 있는 방법이 있습니다.

\[\begin{align} \widehat{\mathbf{A}}_t^{-1} &= \left( \widehat{\mathbf{A}}_{t-1} + \mathbf{x}_{t-1} (\mathbf{x}_{t-1} - \gamma \mathbf{x}_t)^{\sf T} \right)^{-1} \tag{from (9.20)} \\ \\ &= \widehat{\mathbf{A}}_{t-1}^{-1} - \frac{\widehat{\mathbf{A}}_{t-1}^{-1} \mathbf{x}_{t-1} (\mathbf{x}_{t-1} - \gamma \mathbf{x}_t)^{\sf T} \widehat{\mathbf{A}}_{t-1}^{-1}}{1 + (\mathbf{x}_{t-1} - \gamma \mathbf{x}_t)^{\sf T} \widehat{\mathbf{A}}_{t-1}^{-1} \mathbf{x}_{t-1}} \tag{9.22} \end{align}\]

위 식에서 초기값은 $\widehat{\mathbf{A}}_0 \doteq \varepsilon \mathbf{I}$로 정의됩니다. 식 (9.22)은 Sherman-Morrison Formula를 사용한 것이며, 복잡해보이지만 시간 복잡도는 $O(d^2)$에 불과합니다. 이것을 사용해서 LSTD를 시간 복잡도 $O(d^2)$로 구현한 완전한 Pseudocode는 다음과 같습니다.

물론 이렇게 시간 복잡도를 $O(d^2)$로 줄인다고 해도 여전히 Semi-gradient TD보다 훨씬 느립니다. 이러한 시간 복잡도를 감수하더라도 LSTD를 사용하는 것이 그만큼의 가치가 있는지는 $d$가 얼마나 큰지, 학습 속도가 주어진 문제에서 얼마나 중요한지, 시스템의 나머지 부분에서 드는 비용이 어느정도인지에 따라 다릅니다. LSTD는 Step-size Parameter가 필요하지 않다는 장점이 분명 존재하지만, 대신 $\varepsilon$이 필요하며, 이것을 어떤 값으로 정해야하는지에 대한 문제가 존재합니다. $\varepsilon$가 너무 크면 학습 속도가 느려지고, 그렇다고 너무 작으면 역행렬을 계산할 때 문제가 생깁니다. 또한 Step-size Parameter가 없다는 것은 이전에 학습한 내용을 절때 잊지 않는다는 의미가 되는데, 일반적으로 이것이 좋을 수 있지만 강화학습이나 GPI에서 Policy $\pi$가 변하면 문제가 됩니다. 따라서 Policy가 계속 변할 수밖에 없는 Control 문제에서 LSTD를 사용하기 위해서는 이전에 학습한 내용을 잊을 수 있게 다른 메커니즘과 결합되어야만 합니다.

Memory-based Function Approximation

지금까지는 Value Function을 근사화하기 위해 매개변수를 이용하여 접근하는 방법에 대해 다루었습니다. 이러한 접근 방법에서는 매개변수를 조정함으로써 Value Function을 근사하는 학습 알고리즘을 사용하였습니다. 각각의 Update $s \mapsto g$는 근사 오차를 줄이기 위해 매개변수를 조절하는 학습 알고리즘의 예시입니다. Update가 끝나면 학습에 사용되는 Training Data는 폐기될 수 있습니다. 대략적인 State의 Value(Query State)가 필요할 때는 학습 알고리즘에 의해 생성된 최신 매개변수를 사용한 Value Function을 토대로 평가합니다.

이번 Section에서 다룰 Memory-based Function Approximation은 이와 다르게 매개변수를 Update하지 않고, Training Data가 도착할 때마다 메모리에 저장합니다. 그 후 Query State가 필요할 때마다 메모리에서 Training Data를 검색하여 Query State에 대한 Estimated Value를 계산하는 데 사용합니다. 이 방법은 Query State에 대해 시스템이 출력을 제공할 때까지 Training Data의 처리가 연기되기 때문에 Lazy Learning이라고도 합니다.

Memory-based Function Approximation은 매개변수를 사용하지 않는 방법인 Nonparametric Method의 대표적인 예시입니다. 매개변수를 사용하는 방법과 달리 근사 함수가 Linear Function이나 Polynomial과 같은 고정된 종류로 제한되지 않고, Training Data 자체와 Query State에 대한 Estimated Value를 출력하기 위한 수단에 의해 결정됩니다. 더 많은 Training Data가 메모리에 축적될수록 Memory-based Function Approximation은 Target Fucntion을 더 정확하게 근사할 수 있습니다.

이 때, 저장된 Training Data를 선택하는 방법과 Query에 응답하는 데 사용되는 방법에 따라 Memory-based Function Approximation의 종류를 나눌 수 있습니다. 다만 여기에서는 현재 Query State 근처에서만 Local Value Function를 근사하는 Local-learning 방법에 중점을 두겠습니다. 이 방법은 State가 메모리에서 Query State와 가장 가깝다고 판단되는 Training Data를 검색합니다. 이 때 얼마나 가깝다고 판단하는지는 State 간의 거리에 따르는데, 거리에 대한 기준은 문제마다 다양한 방식으로 정의될 수 있습니다. 어쨌든 적절한 Query State의 값을 찾아 제공한 후에는 Local Estimated Value는 삭제됩니다.

Memory-based Function Approximation이 매개변수를 사용하는 근사 방법과 달리 함수의 형태가 정해지지 않기 때문에 많은 데이터가 축적될수록 정확도가 향상됩니다. 이러한 특징으로 인해 Memory-based Function Approximation은 강화학습에 적합하다는 좋은 장점이 있습니다. 예를 들어, Trajectory Sampling은 State Space의 많은 영역에 도달할 수 없거나, 거의 도달할 일이 없기 때문에 전역 근사가 필요하지 않은데, Memory-based Function Approximation을 사용한다면 State의 Local Neighbor에 초점을 맞춤으로써 불필요한 계산 낭비를 방지할 수 있습니다.

이렇게 전역 근사를 피함으로써 얻어지는 또 다른 이점은 Curse of Dimensionality에서 벗어난다는 것입니다. 예를 들어, $k$차원이 있는 State Space의 경우 전역 근사를 저장하는 Tabular 방법에는 $k$에 대해 지수적으로 비례한 메모리가 필요합니다. 하지만 Memory-based Function Approximation을 사용한다면 각각의 데이터는 $k$에 비례한 메모리만 필요하고, $n$개의 데이터를 저장한다면 $n$과 $k$에 대해 Linear에 비례한 메모리가 필요할 뿐입니다. 즉, 지수 함수가 들어가지 않습니다. 다만 이것은 저장하는데 필요한 데이터 양일 뿐, 누적된 데이터의 수가 많아질수록 Query에 응답하기 위해 걸리는 시간이 늘어나기 때문에 대규모 데이터베이스에서 사용하기에는 적합하지 않을 수도 있습니다.

이 문제를 해결하기 위해 최근 Nearest Neighbor 검색을 빠르게 하는 방법이 연구중에 있습니다. 병렬 컴퓨터나 특수 목적 하드웨어를 사용하는 것도 하나의 접근 방식입니다. 소프트웨어적으로는 Training Data를 저장할 때 특별한 다차원 자료구조를 사용하는 것입니다. 대표적으로 $k$차원 공간을 Binary Tree의 노드가 배열된 영역을 재귀적으로 분할하는 $k$-$d$ Tree가 있습니다. $k$-$d$ Tree의 자세한 내용은 Wikipedia에 자세하게 나와있습니다.

Kernel-based Function Approximation

이전 Section에서 설명한 Memory-based Function Approximation에서 Weighted Average과 Locally Weighted Regression과 같은 방법은 State $s’$와 Query State $s$의 거리에 따라 Weight를 부여하여 $s’ \mapsto g$과 같이 적절한 데이터베이스에 매칭됩니다. 이렇게 Weight를 할당하는 함수를 Kernel Function, 또는 그냥 Kernel이라고 부릅니다. Kernel Function $k : \mathbb{R} \to \mathbb{R}$는 State 사이의 거리에 Weight를 할당합니다. 정확하게는 Weight가 거리에 의존할 필요는 없고, State 간의 유사성을 계산하는데 필요한 측정 방식에 따라 의존합니다. 이 경우 $k(s, s’)$ ($k : \mathcal{S} \times \mathcal{S} \to \mathbb{R}$)은 $s$에 대한 Query 응답에 미치는 영향에 대해 $s’$에 대한 Weight가 됩니다.

Kernel Regression은 메모리에 저장된 모든 학습 데이터의 Kernel Weighted Average를 계산하여 Query State에 결과를 할당하는 Memory-based Function Approximation입니다. $\mathcal{D}$가 저장된 학습 데이터의 집합이고, $g(s’)$가 저장된 학습 데이터 중 State $s’$의 Target Function이라고 하면 Kernel Regression에서 다음과 같이 State $s$의 Target Function을 근사할 수 있습니다.

\[\hat{v} (s, \mathcal{D}) = \sum_{s' \in \mathcal{D}} k(s, s') g(s') \tag{9.23}\]

가장 널리 사용되는 Kernel은 Section 9.5.5에 설명한 Gaussian Radial Basis Function (RBF)입니다. RBF는 정규분포처럼 많은 학습 데이터가 존재할 것 같은 지점이 중심이 되고, 학습 중 중심과 너비가 조절됨으로써 균형을 찾습니다. RBF 자체는 매개변수가 RBF의 Weight인 Linear Parametric 방법이며, 일반적으로 Stochastic Gradient Descent나 Semi-gradient Descent로 학습됩니다. RBF Kernel을 사용한 Kernel Regression은 이것과 다르게 Memory-based이고 학습할 매개변수가 없습니다. Query에 대한 응답은 식 (9.23)에 의해 계산됩니다.

Kernel Regression을 실제로 구현하기 위해서는 여기서 다루지 않는 많은 문제가 해결되어야 합니다. 다만 Feature Vector $\mathbf{x}(s) = \left( x_1 (s), x_2 (s), \ldots, x_d (s) \right)^{\sf T}$로 표현되는 State와 Section 9.4에서 설명한 Linear Parametric Regression 방법은 다음과 같이 Feature Vector의 내적 계산으로 간단하게 Kernel Regression을 구현할 수 있습니다.

\[k(s, s') = \mathbf{x} (s)^{\sf T} \mathbf{x} (s') \tag{9.24}\]

식 (9.24)와 같은 Kernel Regression은 동일한 학습 데이터로 학습한 경우 Linear Parametric 방법과 동일한 근사값을 생성합니다. 모든 Kernel Function이 식 (9.24)와 같이 Feature Vector의 내적으로 표현될 수 있는 것은 아니지만, 이렇게 표현할 수 있는 Kernel Function은 같은 결과를 생성하는 Parametric 방법에 비해 간단하게 계산할 수 있는 장점이 있습니다. 이것을 보통 Kernel Trick 이라고 부릅니다. Kernel에 대한 더 자세한 내용은 다음 포스트를 참고해주시기 바랍니다.

• [기계학습] 15. Kernel Methods

Looking Deeper at On-policy Learning : Interest and Emphasis

이번 장에서 지금까지 고려한 알고리즘들은 발생할 수 있는 모든 State를 동등하게 취급했습니다. 그러나 어떤 경우에는 특정한 몇몇 State에 집중해야할 수 있습니다. 예를 들어 Discounted Episodic Task에서 후기 State는 Discount로 인해 초기 State보다 Value가 낮으므로 초기 State를 정확하게 추정하는데 더 집중하는 것이 좋고, Action-Value Function을 학습할 때는 Value가 매우 낮은 나쁜 Action보다 Greedy Action을 더 정확하게 추정하는데 집중하는 것이 좋습니다. Function Approximation을 할 때 사용할 수 있는 자원은 한정되어있기 때문에 원하는 목표를 찾아 집중한다면 성능이 향상될 수 있습니다.

지금까지 발생할 수 있는 모든 State를 동등하게 취급한 이유 중 하나는 On-policy Distribution에 따라 Update했기 때문입니다. 이제는 몇 가지 새로운 개념을 소개함으로써 일반화하고자 합니다.

먼저 음이 아닌 Scalar Measure인 Random Variable $I_t$를 소개합니다. $I_t$는 Interest로 부르며 시간 $t$에서 State(또는 State-Action 쌍)를 정확하게 평가하는 데 얼마나 관심이 있는지에 대한 정도를 나타냅니다. 전혀 신경 쓰지 않는 State라면 Interest는 0이 되고, 가장 크게 신경쓰는 State라면 Interest는 1이 됩니다. (필요하다면 1이 아니라 더 큰 값을 최대값으로 사용해도 됩니다.) Interest $I_t$는 문제에 따라 다양하게 정의할 수 있습니다.

둘째로, 또 다른 음이 아닌 Scalar Measure인 Random Variable인 $M_t$를 소개합니다. $M_t$는 Emphasis로 부르며 시간 $t$에서 수행한 학습을 얼마나 강조할지 나타냅니다. 예를 들어, 식 (9.15)에 Emphasis를 추가한다면 다음과 같이 수정할 수 있습니다.

\[\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1} + \alpha M_t \left[ G_{t:t+n} - \hat{v}(S_t, \mathbf{w}_{t+n-1}) \right] \nabla \hat{v}(S_t, \mathbf{w}_{t+n-1}), \quad 0 \le t < T \tag{9.25}\]

또한 Emphasis와 Interest를 다음과 같이 재귀적으로 관계를 표현할 수 있습니다.

\[M_t = I_t + \gamma^n M_{t-n} \tag{9.26}\]

만약 식 (9.26)을 계산 도중 $t$가 0보다 작아지는 경우 $M_t \doteq 0$으로 정의됩니다. 또한 이 방정식은 $G_{t:t+n} = G_t$, 즉 $n = T - t$, $M_t = I_t$와 같이 Episode의 마지막까지 포함되는 Monte Carlo로 간주됩니다.

Example 9.4) Interest and Emphasis

이번 예제는 Interest와 Emphasis가 얼마나 정확한 Value를 추정할 수 있는지 보여주는 예시입니다. 먼저, 다음과 같이 4개의 State를 가지고 있는 Markov Reward Process가 있습니다.

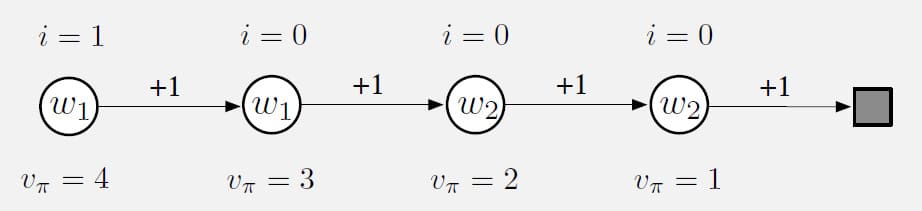
이 예제에서 Episode는 맨 왼쪽 State에서 시작한 다음 최종 State에 도달할 때까지 각 단계마다 +1의 보상을 받은 후, 오른쪽 State로 넘어갑니다. 따라서 첫 번째 State의 Real Value는 4이고, 두 번째 State의 Real Value는 3이 되는 식입니다. (각 State의 Real Value는 State 바로 아래에 표시되어 있습니다.)

하지만 추정된 Value는 매개변수에 의해 제약을 받기 때문에 대략적으로만 구할 수 있습니다. 여기서는 2개의 구성 요소로 이루어진 매개변수 Vector $\mathbf{w} = (w_1, w_2)^{\sf T}$가 주어졌으며, 각 State별 어떤 매개변수를 사용하는지는 State 원 안에 표시되어 있습니다. 처음 두 State는 매개변수가 $w_1$만 주어지므로 Real Value가 다르더라도 동일해야 합니다. 마찬가지로 세 번째와 네 번째의 추정값은 $w_2$만으로 주어졌기 때문에 동일해야 합니다. 만약 가장 왼쪽의 State만 정확하게 평가하는데 관심이 있다고 가정합니다. 그렇다면 State 위에 표시한 것처럼 Interest는 첫 번째 State에만 1이 할당되고 나머지 State에는 0이 할당됩니다.

먼저 이 문제를 Gradient Monte Carlo 알고리즘을 사용해서 해결해보겠습니다. 만약 Interest와 Emphasis를 고려하지 않는다면 매개변수 Vector는 $\mathbf{w}_{\infty} = (3.5, 1.5)$로 수렴합니다. 그러므로 첫 번째 State의 값은 3.5가 됩니다. 반면에 Interest와 Emphasis를 사용한 방법은 첫 번째 State의 값을 정확하게 학습하여 $w_1$은 4로 수렴하고, $w_2$는 Update 되지 않습니다.

다음으로 2-step Semi-gradient TD 방법을 사용해서 해결해보겠습니다. 마찬가지로 Interest와 Emphasis를 고려하지 않는다면 매개변수 Vector는 $\mathbf{w}_{\infty} = (3.5, 1.5)$로 수렴합니다. 만약 Interest와 Emphasis를 추가한다면 매개변수 Vector는 $\mathbf{w}_{\infty} = (4, 2)$로 수렴합니다. 이것은 첫 번째 State와 세 번째 State에 대해 정확한 Value를 계산하지만, 두 번째와 네 번째 State의 Update는 수행하지 않습니다.

□

Summary

강화학습을 인공지능이나 대규모 응용 프로그램에 적용하려면 일반화가 가능해야 합니다. 일반화를 하기 위해서는 각각의 Update를 Training Data로 취급하여 Supervised Learning을 이용한 Function Approximation을 사용할 수 있습니다. 다행히, Supervised Learning에서 이미 연구된 많은 Function Approximation 방법이 있기 때문에, 기존 방법을 사용하여 이 문제를 해결할 수 있습니다.

우선 가장 적합한 Supervised Learning 방법으로 생각되는 것은 Policy가 Weight Vector $\mathbf{w}$를 매개변수로 하는 Parameterized Function Approximation을 사용하는 방법입니다. Weight Vector에는 많은 구성 요소가 있지만, State Space은 이보다 더 클 수밖에 없기 때문에 Approximate Solution을 찾아야 합니다. 이 때 On-policy Distribution $\mu$에서 Weight Vector $\mathbf{w}$를 사용하여 추정한 Value Function $v_{\pi_{\mathbf{w}}} (s)$가 Real Value Function와 얼마나 다른지를 측정하기 위해 Mean Square Value Error $\overline{\text{VE}}$를 정의했습니다. $\overline{\text{VE}}$는 On-policy에서 서로 다른 Estimated Value Function의 우열을 매길 수 있는 명확한 판단 기준을 제공합니다.

좋은 Weight Vector를 찾기 위해 가장 많이 사용되는 방법은 Stochastic Gradient Descent (SGD)입니다. 특히 이번 장에서는 고정된 Policy가 있는 On-policy 경우에만 중점을 두었습니다. 이 경우에 사용하는 학습 알고리즘은 $n = \infty$일 때 사용되는 Gradient Monte Carlo 알고리즘, 그리고 $n = 1$일 때 사용되는 Semi-gradient TD(0) 알고리즘입니다. Semi-gradient TD는 엄밀하게 말하면 Gradient 방법이 아니지만, 이러한 Bootstrapping 방법에서 Weight Vector가 Update 대상에 나타나지만 Gradient 계산에서는 고려되지 않으므로 Semi-gradient 방법이라고 부릅니다.

그럼에도 불구하고 Feature에 Weight를 곱해 각각 더한 Linear Function Approximation 같은 특수한 경우라면 Semi-gradient 방법은 좋은 Estimated Value를 얻을 수 있습니다. Linear Function Approximation은 간단하지만 적절한 Feature가 선택되었을 때 잘 동작한다는 장점이 있습니다. 이 때, Feature를 선택하는 것은 강화학습 시스템에 사전 지식을 추가하는 가장 중요한 방법 중 하나입니다. Polynomial을 선택할 경우, 온라인 학습 환경에서 일반화하기 힘든 단점이 있습니다. 온라인 학습을 원할 경우 Fourier-based나 Coarse Coding을 선택하는 것이 좋습니다. Tile Coding은 Coarse Coding의 한 종류로, 계산이 효율적이고 유연한 것이 특징입니다. Radial Basis Function은 부드럽게 변화하하는 1차원, 혹은 2차원 작업에 적합합니다. Least Square TD는 가장 데이터적으로 효율적인 Linear TD 추정 방법이지만 계산량이 매우 많은 단점이 있습니다. non-Linear Method에는 SGD와 Backpropagation이 결합한 Artificial Neural Network가 있습니다. 이 방법은 최근 Deep Reinforcement Learning이라는 이름으로 활발히 연구되고 있습니다.

Linear Semi-gradient $n$-step TD는 일반적인 조건에서 모든 $n$에 대해 최적의 오차 범위 내에 있는 $\overline{\text{VE}}$에 수렴하는 것이 보장됩니다. $\overline{\text{VE}}$는 $n$이 클수록 더 작아지며(=범위가 좁아지며), $n \to \infty$일 때 0에 수렴합니다. 하지만 $n$이 커질수록 학습 속도가 매우 느려지는 문제가 있습니다.

다음 장에서는 근사를 사용하는 On-policy Control에 대해 알아보도록 하겠습니다.

9장에 대한 내용은 여기서 마치겠습니다. 읽어주셔서 감사합니다!