Theory of Generalization

6장에서는 지난 장에서 다루었던 $m_{\mathcal{H}}$에 대한 증명들을 배우게 됩니다.

증명을 다루는 만큼, 이번 장은 가장 이론적인 내용을 담고 있습니다. 수학식이 많이 나오기 때문에 다소 지루할 수 있다는 것을 미리 말씀드립니다.

Outline

이번 장의 증명은 크게 두 가지로 나뉘어 있습니다.

첫째는 $m_{\mathcal{H}}$가 다항 함수인 것을 증명하는 것이고, 두 번째는 $m_{\mathcal{H}}$가 Hoeffding’s Inequality에서 $M$을 대체하기 위한 증명입니다. 이전 장까지 계속 Hoeffding’s Inequality에서 오른쪽 항의 값이 1보다 큰 것이 문제였기 때문에 이것을 해결하기 위한 과정이라고 생각하시면 됩니다.

Proof that $m_{\mathcal{H}}$ is polynomial

$m_{\mathcal{H}}(N)$이 $N$에 대해서 다항함수임을 증명하려면, 부등식을 통해 $m_{\mathcal{H}}(N)$이 $N$으로 이루어진 다항식보다 작거나 같다는 것을 증명하면 됩니다. 다항식의 차수를 걱정하실 수도 있지만, 다항식의 차수가 어떻든 $N$이 충분히 커지게 되면 지수함수 보다 작아지기 때문에 차수 자체는 큰 문제가 아닙니다.

본 증명을 하기 앞서 새로운 함수인 $B(N, k)$를 정의합니다. 이것은 $N$개의 점이 있고 Break Point가 $k$일 때 가능한 Dichotomy의 최대 개수를 의미합니다.

방금 정의한 $B(N, k)$ 함수를 구체적인 변수들로 표현하기 위해 위 슬라이드의 오른쪽 표를 참고하여 따라가보겠습니다. 오른쪽 표에서 $\mathbf{x}_1, \mathbf{x}_2, …, \mathbf{x}_N$은 각각 $N$개의 점을 의미합니다. 이 값은 분류된 결과를 의미하므로 +1이나 -1의 값을 가질 수 있습니다.

가능한 Dichotomy 들의 조합 중에서, $\mathbf{x}_1, …, \mathbf{x}_{N-1}$ 까지의 값은 같고, $\mathbf{x}_N$의 값만 정 반대인 집합을 $S_2$라고 정의하고, 그렇지 않은 것들을 모아둔 집합을 $S_1$이라고 정의하겠습니다. 그럼 모든 Dichotomy 들의 조합들은 $S_1$이나 $S_2$ 둘 중 하나에 포함될 것이라는 것을 쉽게 알 수 있습니다.

그 중에서 $S_2$를 좀 더 세분화하기 위해, $\mathbf{x}_N$의 값이 +1인 것들의 집합을 $S^+_2$이라 하고, $\mathbf{x}_N$의 값이 -1인 것들의 집합을 $S^-_2$라고 하겠습니다. 당연히 $S^+_2$와 $S^-_2$의 갯수는 같을 수밖에 없습니다.

$S_{1}$의 원소의 개수를 $\alpha$라고 하고, $S^+_2$, $S^-_2$의 원소의 개수를 각각 $\beta$라고 하면 $B(N, k)$의 값은 $\alpha + 2\beta$로 표현이 가능합니다.

이제 점 $\mathbf{x}_{N}$을 삭제해보겠습니다. 다시 말해 $N-1$개의 점에서 Break Point가 $k$일 때 $B(N-1, k)$를 구하자는 것입니다. 직관적인 생각으로는 $\alpha + \beta = B(N-1, k)$가 되는 것일텐데, 왜 $\alpha + \beta \leq B(N-1, k)$인지 의문이 들 수도 있습니다.

그 이유는 $B(N-1, k)$는 가능한 Dichotomy의 최대 개수라고 정의되었기 때문입니다. 방금처럼 점이 $N$개였던 표에서 $\mathbf{x}_{N}$만 지운 표가 점이 $N-1$일 때의 Dichotomy의 최대 개수인지 아니면 일부분인지 모르기 때문에 등호가 아닌 부등호가 들어간 것입니다.

마찬가지로 이번에는 $B(N-1, k-1)$을 구해볼 것인데, 역시 점이 $N-1$개이므로 표에서 점 $\mathbf{x}_{N}$을 삭제해보겠습니다. 이전 슬라이드와 마찬가지로 $B(N-1, k-1)$가 $\beta$ 이상이라고 부등호가 되어있는데, 왜 이것이 $k-1$의 Break Point를 가지는지 직관적으로 이해하기 쉽지 않습니다.

만약에 $\beta$가 $k$개의 Break Point를 가진다고 가정한다면, Break Point의 정의에 의해서 $2^{k-1}$개의 Dichotomy를 표현 가능해야 합니다. 그러나 처음 가정으로 $B(N, k)$이 $k$개의 Break Point를 가지고 있기 때문에 그것의 일부분인 $\beta$는 $k$개의 Break Point를 가질 수 없습니다. (즉, $\mathbf{x}_{N}$을 추가했을 때 $2^{k}$개의 Dichotomy를 표현한다는 것에 모순입니다.)

반대로 $\beta$가 $k-1$개의 Break Point를 가진다는 것을 보이는 것은 쉽습니다. $S^+_2, S^-_2$는 $\mathbf{x}_N$의 값을 제외하면 나머지 $\mathbf{x}_1, \mathbf{x}_2, … \mathbf{x}_N$ 요소가 같은 값이기 때문입니다.

이전의 두 슬라이드의 내용을 정리해보면 다음과 같습니다.

\[B(N, k) = \alpha + 2\beta\] \[\alpha + \beta \leq B(N-1, k)\] \[\beta \leq B(N-1, k-1)\]

따라서 위 식에서 두 번째 식과 세 번째 식을 양변을 더해주면 아래와 같은 식을 유도할 수 있습니다.

\[B(N, k) \leq B(N-1, k) + B(N-1, k-1)\]

이를 토대로 임의의 $N$, $k$에 대해서 $B(N, k)$의 값을 Recursive하게 계산할 수 있다는 것을 알 수 있습니다.

방금 유도한 식을 토대로 $N$과 $k$에 따라 $B(N, k)$값이 어떻게 변하는지 위 슬라이드의 오른쪽 표에 나와있습니다. 표를 채우려면 먼저 $B(N, 1)$과 $B(1, k)$를 구해야 하는데, $B(N, 1)$은 점이 몇 개가 주어지든 Break Point가 1이란 얘기니까 무조건 딱 한 가지로만 분류가 가능하다는 뜻입니다. 따라서 $B(N, 1)=1$이 됩니다.

이번엔 $B(1, k)$를 계산해야 하는데, 점이 딱 1개만 있으면 어차피 나눌 수 있는 경우의 수는 +1 또는 -1 밖에 없으니까 Break Point가 아무리 커봤자 $B(1, k)=2$라는 것을 쉽게 알 수 있습니다. (단, $k=1$일 때 제외)

이렇게 첫 번째 행/열만 채우게 되면 나머지는 이전 슬라이드에서 보였던 부등식을 통해 채울 수 있습니다. 이 표의 값들을 보실 때 주의하실 점은, $B(N, k)$의 정확한 값이 아니라 Upper Bound (상한)이라는 겁니다. 애초에 유도한 재귀식 자체가 부등식이기 때문이죠.

즉 표의 값을 읽을 때, 예를 들면 표에서 붉은 글씨를 확인해 보시면 $B(3, 2)$이 4라고 나와있습니다. 이 말은 $B(3, 2)$가 정확하게 4라는 뜻이 아니라 아무리 커봤자 최대가 4라는 뜻입니다. 물론 4보다 작을 수도 있습니다. (이건 직접 하나하나 계산해보기 전까지는 모릅니다.)

그럼 실제로 $B(3, 2)$의 값이 뭔지 궁금합니다. 운이 좋게 이것은 저희가 이미 계산해본 적 있습니다. 5장의 맨 마지막 슬라이드에서 간단한 Puzzle을 풀었었는데, 이때가 $N=3, k=2$의 예제였습니다. 계산했을 때 값이 4가 나왔었는데, 우연히도 $B(3, 2)$의 Upper Bound와 같은 값임을 알 수 있습니다. 하지만 이것은 우연일 뿐, 항상 이렇게 같은 값이 나오지는 않음에 유의하셔야 합니다.

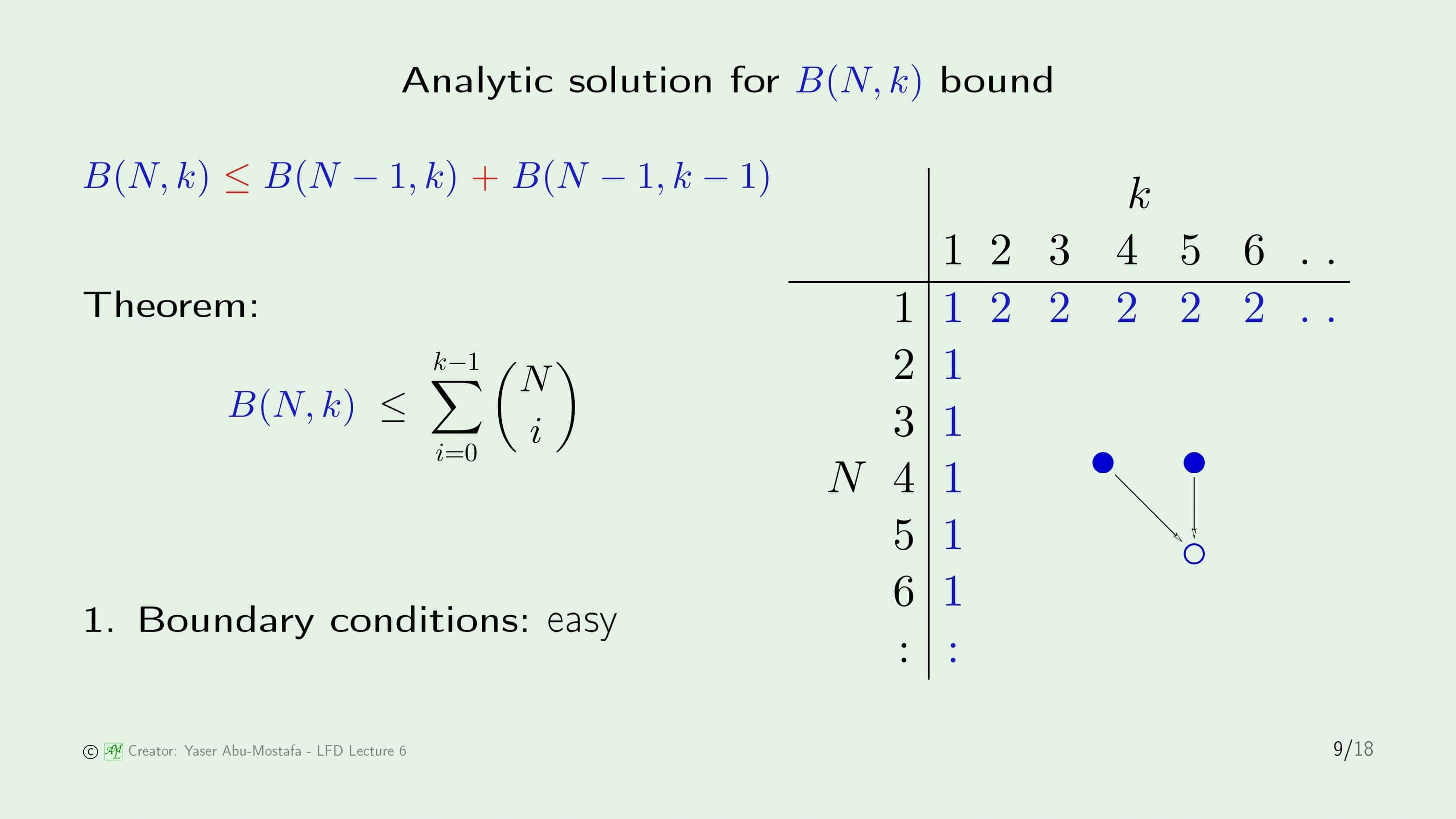
하지만 이렇게 Recursive하게 계산하는 것은 계산 속도도 오래 걸리고 귀찮기 때문에, 이를 한 번에 표현할 수 있는 일반항을 찾아야 합니다. 위 슬라이드에 나온 것처럼, $B(n, k)$에 대한 일반항을 조합(Combination)들의 합으로 제시하고 이를 증명합니다.

증명 방법은 흔히 사용하는 Induction (귀납법)으로 증명합니다. 먼저 맨 처음 항이 True임을 보여야 하는데, 이건 그냥 $N=1$과 $k=1$을 각각 넣게 되면 참임을 알 수 있습니다.

그다음의 과정이 조금 흥미로운데, 여기서는 $B(N-1, k)$의 합과 $B(N-1, k-1)$의 합이 $B(n, k)$가 되는지를 보였습니다. 첫 번째 줄에서 두 번째 줄로 넘어갈 때는 두 항을 합치기 위해 시그마를 똑같이 $i=1$부터 $i=k-1$까지 맞춰눈 것이고, 세 번째 줄에서 네 번째 줄로 넘어간 것은 조합에서 사용하는 파스칼의 삼각형을 사용해서 두 개의 조합을 하나로 합친 것입니다.

이 외에는 단순한 계산이기 때문에 생략하겠습니다.

최종적인 결론입니다. 이전 슬라이드까지의 과정을 통해서 결국 $m_{\mathcal{H}}$가 조합들로 이루어진 합보다 작다는 것이 증명되었고, 이 조합은 아무리 커봤자 $N^{k-1}$의 항을 가진 다항함수이므로 결과적으로 그토록 원하던 Growth Function이 다항함수(Polynomial)이다 라는 결론이 나온 것입니다.

지금까지 Hoeffding’s Inequality가 무한대에 가까운 $M$으로 고통받았던 것을 생각해보면 Growth Function을 통해 다항함수 꼴로 줄인 것은 매우 큰 의미가 있습니다.

왜 그것이 큰 의미가 있는지 이 슬라이드를 통해 설명할 수 있습니다. 이전 장에서 Growth Function을 설명할 때 사용한 3가지 예제가 기억나실 겁니다. (Positive Ray, Positive Interval, Convex Set)

이 중에서 Positive Ray와 Positive Interval은 지난 장에서 직접 계산했기 때문에, 방금 유도한 Growth Function의 Upper Bound와 비교해 보겠습니다. 운이 좋게 Positive Ray와 Positive Interval은 Upper Bound와 똑같이 나왔습니다만, 아까도 말씀드렸듯이 항상 똑같은 게 아니라는 걸 꼭 기억하셔야 합니다.

그런데 2D Perceptron은 이전에 Break Point가 4인 것은 보였지만, Growth Function을 직접 구할 수는 없었습니다. 하지만 방금 유도한 Growth Function의 Upper Bound를 이용하면 2D Perceptron도 공식에서 나온 다항함수보다 작다는 것을 보일 수 있습니다.

결국 이런 방식을 통해 그 어떠한 케이스에서도 Break Point만 찾으면 Growth Function이 다항함수 꼴로 Upper Bound가 정해진 다는 것을 알 수 있습니다.

Proof that $m_{\mathcal{H}}$ can replace $M$

그럼 지금까지 $m_{\mathcal{H}}$가 다항함수로 이루어진 식의 Upper Bound로 이루어진 것이 증명되었으니, 이제 정말 중요한 Hoeffding’s Inequality에 있던 $M$ 대신에 $m_{\mathcal{H}}$를 대입하기 위한 증명이 필요합니다.

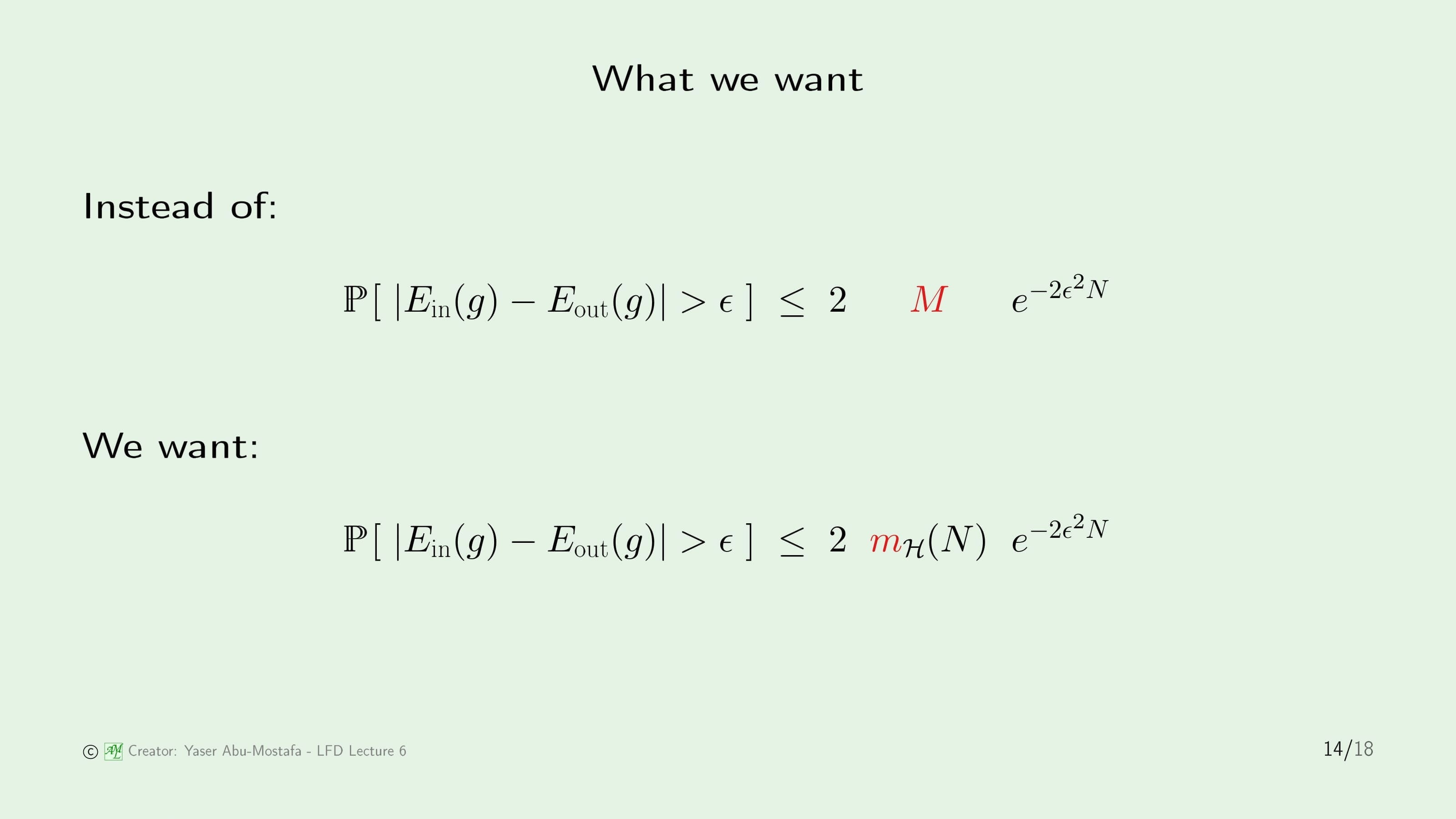
사실 우리가 원하는 결과는 Hoeffding’s Inequality에서 $M$ 자리에 그대로 $m_{\mathcal{H}}$가 들어가는 것이지만, 안타깝게도 $M = m_{\mathcal{H}}$는 말이 안 돼니 직접적으로 교체할 수는 없습니다.

어쨌든 이 $M$ 대신에 $m_{\mathcal{H}}$를 넣어 변형된 식을 증명해야겠지만, 강의에서는 이 증명이 너무 복잡하기 때문에 부록에 따로 빼놓았다고 합니다. 제가 확인해보니 6페이지 정도 분량이라 저도 안 읽었습니다. 굳이 그것까지 읽지 않아도 될 거 같았거든요.

강의에서는 간단하게 증명의 핵심 정도만 언급하고 넘어갑니다. 증명의 핵심은 크게 3가지인데, (1) $m_{\mathcal{H}}$를 어떻게 대입할 것인가, (2) $E_{out}$은 어떻게 되는가, (3) 그리고 이를 합치는 과정입니다.

먼저 Hoeffding’s Inequality에서 $M$이 어떻게 나왔는지와 이를 어떻게 바꾸는지에 대한 대략적인 그림입니다.

가운데 그림이 바로 Hoeffding’s Inequality에서 $M$이 곱해진 이유인데, 각각의 Bad Event를 모두 배반 사건으로 가정하고 Union Bound를 씌웠기 때문입니다. 하지만 직관적으로 생각해 보았을 때, 이 Bad Event들이 모두 배반 사건이라고 놓는다면 너무 비관적인 가정이라고 생각이 듭니다. 아마 맨 오른쪽처럼 대부분의 Event가 겹치게 될 텐데, 이를 보이는 것은 다음 장인 VC Dimension에서 다루게 될 예정입니다.

지금은 그냥 저런 식으로 해결되겠구나~라고만 생각하시면 되겠습니다.

두 번째로는 $E_{out}$에 대해 수행할 작업입니다. 이 그림은 2장에서 다룬 적이 있습니다. 그 때와 마찬가지로 통(Bin)안의 구슬들을 잘못 분류한 것은 Out of Sample Error이고 이 중 몇 개의 구슬을 뽑은 것 중 잘못 분류한 것은 In Sample Error입니다. 증명에서는 기존에 하나만 뽑던 Sample을 독립적으로 한 개 더 뽑는 방법을 사용합니다. (물론 두 Sample은 같은 확률 분포를 사용하여 뽑습니다) 다만 독립적으로 Sample을 뽑았다고 할 지라도 두 Sample은 같은 통 안에서 같은 확률 분포를 사용하여 뽑았기 때문에 서로 관련이 생기게 됩니다. (이 말은 빨간색 구슬의 비율이 비슷하다는 뜻입니다) 강의에서는 통이 1개일 때는 Sample을 한 개 뽑든 두 개 뽑든 차이가 없지만, 여러 개의 통을 가정한 상황에서는 $E_{out}$과 $E_{in}$의 관계가 좀 더 가까워지기 때문에 이런 방법을 사용했다고 합니다.

마지막에서는 이를 모두 합쳐서 최종적으로 변한 식입니다. 이 식을 The Vapnic-Chervonenkis (VC) Inequality라고 합니다.

슬라이드에 나타난 식을 보시면 $M$이 $m_{\mathcal{H}}$가 교체된 것 외에도 이것저것 바뀌었음을 알 수 있습니다. 가령 $N$이 $2N$으로, $m_{\mathcal{H}}$ 앞의 계수가 2에서 4로 바뀌었고, 지수에서 2가 8분의 1로 바뀌었죠. ($N$이 $2N$으로 바뀐 이유는 지난 슬라이드에서 Sample을 두 개 뽑았기 때문입니다.)

왜 이렇게 바뀌었는지 궁금하시면 책 부록에 첨부된 증명을 보시면 될 것 같습니다…만 사실 저도 증명을 읽어보지 않아서, 그냥 이렇게 바뀌는구나 라고만 이해하시고 그것보다 중요한 VC Bound에 더 중점을 둬야 할 것 같습니다. 이어지는 VC Dimension에서 이 VC Bound에 대해 더 자세히 다뤄질 예정입니다.

이번 장은 여기까지입니다. 감사합니다.