Training versus Testing

5장에서는 Training과 Testing이 어떻게 다른지 다루게 됩니다. 핵심은 2장에서 다루었던 Hypothesis의 수인 $M$을 어떻게 효과적으로 줄일 수 있는가 하는 것입니다.

Outline

이번 장의 구성은 제목과 같이 Training에서 Testing으로 넘어가면서 생기는 문제에 대해 알아보고, Hypothesis의 수를 줄이기 위해 Dichotomies, Growth function 등의 개념을 설명합니다. 그 다음에는 예제를 통해 Growth function을 계산하는 법을 알아보고, Break Point의 개념을 익히며, 마지막으로 간단한 퍼즐을 풀고 마치게 됩니다.

From training to testing

2장에서 배웠던 Hoeffding’s Inequality를 복습해봅시다. Testing의 경우에는 Final Hypothesis 1개만을 가지고 만든 식이었기 때문에 원래의 Hoeffding’s Inequality와 같았습니다. 그러나 Training의 경우에는 모든 Hypothesis들에 대해 각각 Hoeffding’s Inequality가 적용되었으므로 이들의 개수인 $M$을 오른쪽에 곱해줬었습니다. 여기서 발생하는 문제는, 실질적으로 Hypothesis의 수가 거의 무한하므로 오른쪽 항이 1을 넘기가 너무 쉬워 부등식 자체가 큰 의미를 갖지 못한다고 배웠습니다.

이번 장에서는 이 $M$ 대신에 보다 의미 있는 다른 값을 넣기 위해 알아보는 시간입니다.

먼저 이 $M$이란 값이 어디서 왔는지부터 다시 한번 점검해보겠습니다. Hoeffding’s Inequality에서 확률 $P$ 안에 들어있는 것은 Bad Event였습니다. 이 Bad Event라는 것은 Hypothesis에서 In Sample Error와 Out of Sample Error의 차이가 $\epsilon$ 값보다 크다로 정의되어 있었습니다. 그래서 모든 가능한 $M$개의 Hypothesis에서 이러한 보장이 필요했기에, 최악의 경우(즉, 모든 Bad Event가 서로 배반 사건일 경우)를 감안하여 각각의 Bad Event가 일어날 확률을 그냥 더해줬었습니다.

그런데 Hypothesis에서 Bad Event가 일어나는 사건들이 배반 사건이 아닐 가능성이 높다는 겁니다. 실제로는 위 슬라이드의 오른쪽 그림처럼 어느 정도 겹쳐 나올 확률이 훨씬 큽니다.

이해를 돕기 위해 우리가 잘 아는 Perceptron에서 예제를 하나 만들어보겠습니다. 먼저, 위 슬라이드의 오른쪽 그림과 같이 한쪽은 -1, 다른 한쪽은 +1로 깔끔하게 분리되는 Classification 문제가 있다고 가정해봅시다. 이 중 하나의 Hypothesis로, 파란색 선이 존재합니다. 보이시는 대로 정확하게 나누지 않았기 때문에 Error가 존재합니다. 그렇다면 위 예제에서 In Sample Error와 Out of Sample Error를 각각 찾아봅시다. 이 파란색 선의 In Sample Error와 Out of Sample Error는 어떻게 계산할 수 있을까요?

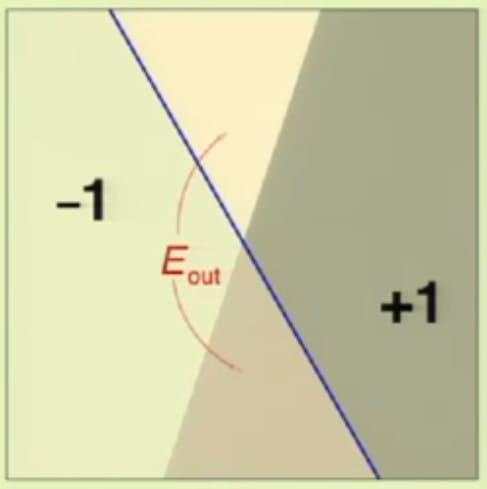
먼저 Out of Sample Error는 위의 그림과 같이 잘못 나눈 부분의 영역입니다. In Sample Error는 아래처럼 주어진 Data가 있을 때 잘못 판단이 된 Data Point의 수로 정의됩니다. (4장을 참고하세요.)

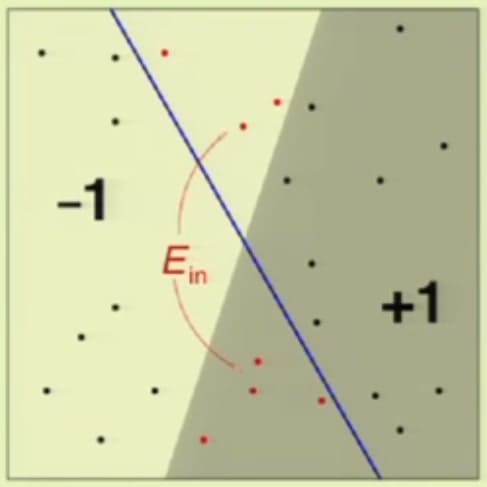
자, 이렇게 In Sample Error와 Out of Sample Error를 각각 계산했으니, 이제 다른 Hypothesis를 한번 따져봅시다. 위 슬라이드(5번 슬라이드)에서 파란색 선을 살짝 비튼 초록색 선을 또다른 Hypothesis라 볼 수 있습니다.

이 두 Hypothesis의 차이는 그림에서의 노란색 면적임을 쉽게 알 수 있습니다. 그런데 전체적으로 보았을 때 이 면적이 매우 미미하므로, 이 두 Hypothesis는 상당히 유사함을 알 수 있습니다. 이와 비슷한 Case가 매우 많다는 것을 직관적으로 알 수 있으므로, 모든 Hypothesis에 대해 Hoeffding’s Inequality를 Union Bound로 잡는 것은 상당히 불합리하다고 생각할 수 있습니다.

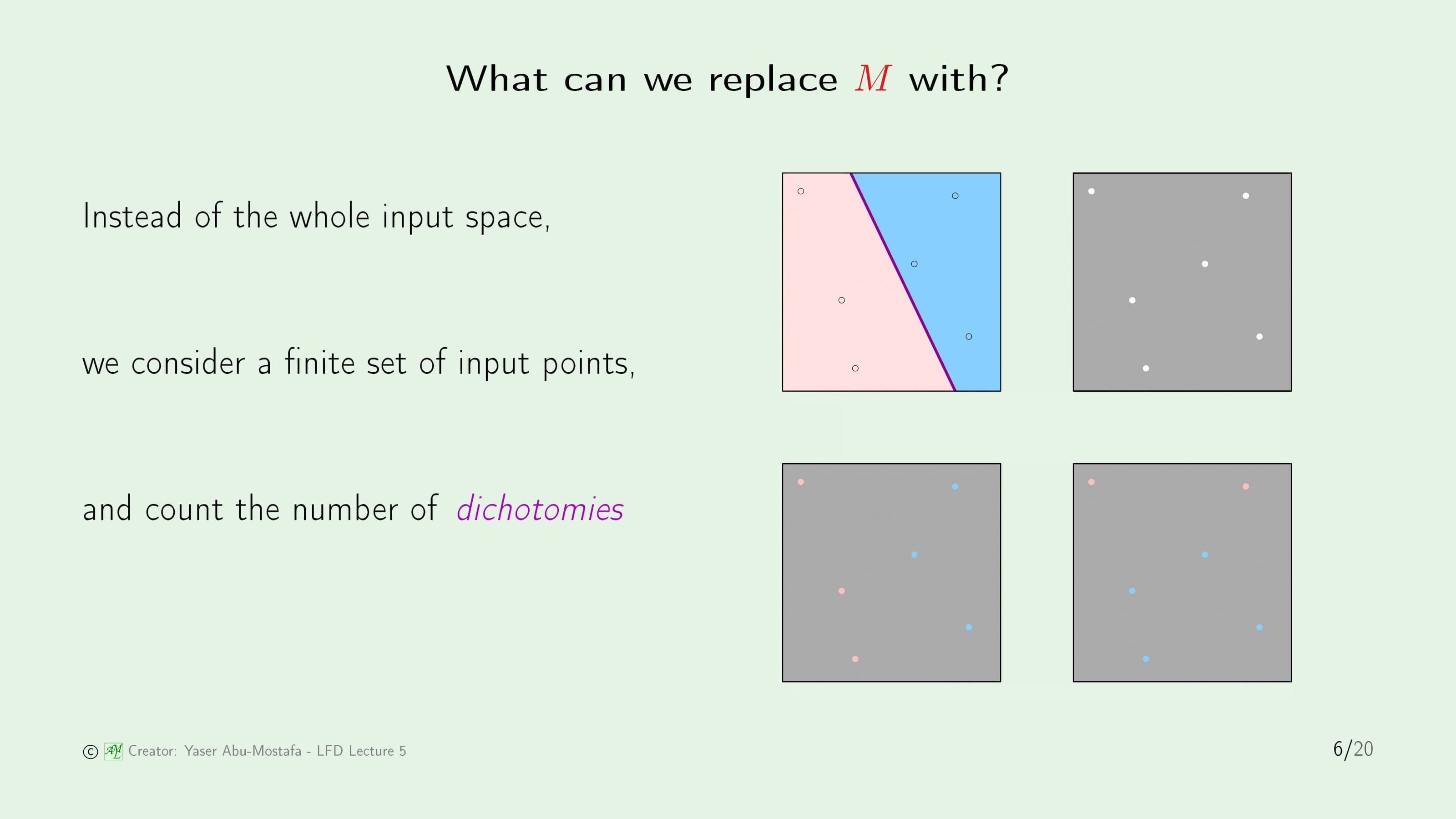
방금 전 슬라이드에서 In Sample Error를 계산했던 방법을 자세히 살펴보겠습니다. 일반적으로, Out of Sample Error를 정확하게 계산할 수 있는 방법은 없습니다. 2장에서도 나왔지만, 기계학습이라는 것은 항상 전체의 데이터를 갖지 못한 상황만을 가정하기 때문입니다. (전체의 데이터가 있다는 것은 굳이 기계학습을 사용할 의미가 없다는 뜻이기 때문입니다.)

그렇기 때문에 In Sample Error의 상황만을 따져보겠습니다. 전체의 영역은 연속적인 공간입니다. 하지만 이 전체의 공간을 하나하나 따질 수 없으므로, 몇 개의 점만을 가지고 계산하고자 합니다. 즉, 전체의 영역이 어떻게 구분되었나를 따지기보다는 우리가 선택한 해당 점들이 어떻게 분류가 되었나를 확인합니다. 이러한 점들을 Dichotomies 라고 합니다. 위 슬라이드에서 오른쪽 그림이 의미하는 것은 첫 번째 그림과 같은 상황일 때, 두 번째 그림과 같이 몇 개의 구멍이 뚫린 불투명한 덮개가 있다고 가정합니다. 그리고 세 번째 그림은 이 덮개를 첫 번째 그림에 덮은 상황입니다. 이 세 번째 그림을 보시면 보라색 선이 보이지 않습니다. 따라서 영역을 어떻게 나누었나(=보라색 선이 어디에 있는가)에 관심을 갖기보다는 우리가 선택한 Data Point들이 어떻게 분류가 되었나를 본다는 것이 핵심입니다.

그렇다면 Classification 문제에서 Dichotomy의 수가 얼마나 되는지 알아봅시다. Hypothesis는 모든 데이터 공간 $\mathcal{X}$를 +1 또는 -1로 분류합니다. 그런데 Dichotomy는 $N$개의 Data Point를 각각 +1 또는 -1로 분류합니다. 따라서 Hypothesis의 숫자는 무한할 수 있지만, Dichotomy의 숫자는 아무리 많아봤자 $2^N$개밖에 나올 수가 없습니다. 그렇다면 Dichotomies는 최소한 유한하다는 보장이 있으니 Hoeffding’s Inequality에서 $M$ 대신에 사용할 수 있음을 알 수 있습니다.

이제 새로운 함수를 하나 배워보겠습니다. 방금과 같이 $N$개의 Data Point가 있을 때, 나올 수 있는 최대의 Dichotomies의 수를 Growth Function 이라고 합니다. 이전 슬라이드에서 언급한 것처럼, Dichotomies의 수는 아무리 많아봐야 $2^N$개 이므로, Growth Function의 최댓값도 $2^N$가 됩니다.

간단한 예제 몇 가지를 통해 Growth Function을 구하는 방법을 알아보겠습니다. 2D Perceptron 문제에서 Growth Function을 계산해보겠습니다.

먼저 $N=3$일 때를 확인해 봅시다. 첫 번째 그림처럼 Data Point가 놓여있을 경우, 각각의 Data를 어떤 방식으로 +1이나 -1로 정의해도 모두 선 하나로 구분할 수 있습니다. 따라서 $m_{\mathcal{H}}(3)=8$임을 알 수 있습니다.

그런데 두 번째 그림과 같은 상황을 생각해서 의문을 가질 수도 있습니다. 두 번째 그림처럼 점 3개를 일렬로 놓으면 절때로 선 하나로 Data Point를 구분할 수가 없기 때문입니다. 하지만 Growth Function은 최대의 Dichotomies의 수만을 따지기 때문에, 설사 단 한 가지의 경우만 8개가 나올 수 있다고 해도 Growth Fucntion의 값은 8이 되는 겁니다.

이번엔 $N=4$인 경우를 보시면, 이 경우에는 어떻게 점을 놓더라도 세 번째 그림처럼 선 하나로는 절대 점들을 구분할 수 없는 경우가 나옵니다. 따라서 이 경우에는 최대치인 16개가 될 수 없고, 저렇게 십자 모양으로 데이터가 분산된 경우(+1과 -1이 뒤바뀌는 경우도 있으니 실제로는 2가지 경우입니다)를 제외한 14개의 경우만 구분이 가능합니다. 따라서 $m_{\mathcal{H}}(4)=14$가 됩니다.

Illustrative examples

Growth Function을 계산하는 방법은 알았지만, 이제 또 다른 문제가 생겼습니다. Growth Function이 최대의 Dichotomies의 수를 구해야 하는거면 일일이 해봐야만 알 수 있는 건데, 그러면 $N$이 커질 때는 어떻게 이걸 일일이 구해야 할지 막막합니다. 안타깝게도 일반적인 케이스는 진짜 일일이 해보지 않고는 모릅니다만, 많이 보이는 몇 가지 예제는 간단한 공식으로 계산할 수 있습니다. 다음 슬라이드에서 몇 가지 예제를 통해 Growth Function을 구해보겠습니다.

첫 번째 예제는 Positive Ray입니다. 이것은 데이터가 모두 일직선 위에 놓여있고, 점 $a$를 기준으로 왼쪽은 모두 -1로, 오른쪽은 모두 +1로 분류되는 경우입니다.

이 상황에서는 나올 수 있는 경우의 수를 따져봅시다. 간단히 이를 계산하려면 점 $a$가 놓일 수 있는 위치가 몇 개나 있을지 세어보는 겁니다. 하나하나 따져보면 $x_1$ 왼쪽에 있는 경우 (1개) + 연속된 두 점 $x_i$, $x_j$ 사이에 있는 경우 ($N-1$개) + $x_N$ 오른쪽에 있는 경우 (1개) 이므로 다 합치면 $N+1$개가 됨을 알 수 있습니다.

즉, Positive Ray에서 Growth Function의 값은 $N+1$이 됩니다.

두 번째 예제는 Positive Interval입니다. 이 예제는 방금 전 예제처럼 데이터들이 일직선 위에 놓여있는 상황인데, +1이 되는 조건이 임의의 구간으로 설정되어 있습니다.

이 상황에서 나올 수 있는 경우의 수를 계산하려면, 이전 예제에서 점 $a$를 두 개 잡아 그 사이를 +1로 설정하면 됩니다. 따라서 총 $N+1$개의 구간에서 두 점을 잡고, 그 순서는 중요하지 않으니 Combination (조합)으로 계산하면 됩니다. 즉, $N+1 \choose 2$가 됩니다.

마지막으로 놓치지 말아야 하는 경우에 수가 있습니다. 똑같은 구간에서 두 점을 잡게 되면 실질적으로 +1이 되는 점이 한 개도 없으므로, 이것도 경우에 수에 추가해야 합니다. 따라서 Positive Interval에서 Growth Function의 값은 $N+1 \choose 2$ + 1이 됩니다.

마지막 예제는 Convex Set입니다. Convex Set은 임의의 집합에서 두 점을 잡았을 때, 그 두 점을 잇는 선분도 그 집합 내의 영역안에 있는 집합을 말합니다.

이 예제에서는 오른쪽 그림과 같이 원 위에 임의의 Data Point를 잡은 상황입니다. 이러한 Convex Set에서는 각각의 점이 +1이든 -1이든 상관없이 오른쪽 그림처럼 임의의 다각형을 만들 수 있습니다. 따라서 이때는 모든 경우를 표현 가능하므로, Convex Set에서의 Growth Function의 값은 최댓값인 $2^N$개가 되는 것입니다.

방금까지 살펴본 3가지 예제의 Growth Function을 정리하면 위 슬라이드와 같습니다.

그럼 이제 이번 강의 초반에서 언급했던 Hoeffding’s Inequality를 다시 따져봅시다.

우리가 최종적으로 원하던 것은 이 $M$을 다른 것으로 대체하는 것이었는데, 지금 괜찮은 대안으로 Growth Function $m_{\mathcal{H}}(N)$ 이 나왔습니다. 무한대일 수도 있는 $M$보다는 낫지만, Growth Function은 Convex Set 같은 경우처럼 데이터에 지수함수꼴로 비례하는 최악의 경우가 있기 때문에 역시 부등식의 오른쪽 항이 1보다 커질 위험이 있습니다. 만약에 이 Growth Function이 데이터 $N$에 대해 Polynomial 하다는 것만 밝혀낸다면, Hoeffding’s Inequality를 훨씬 괜찮게 바꿔줄 수 있을 것 같습니다.

Key notion : Break point

이 문제를 해결하기 위해 Break Point라는 것을 배워보겠습니다.

만약에 $\mathcal{H}$에서 $k$개의 데이터를 골고루 흩뿌릴 수 없을 때 이 $k$를 $\mathcal{H}$에서의 Break Point라고 합니다. 정의가 직관적으로 이해되지 않기 때문에 조금 더 쉽게 설명해 드리겠습니다. 데이터를 골고루 흩뿌릴 수 없다라는 말은 데이터를 어떻게 배치해도 최대의 Dichotomies를 만들 수 없는 상황을 말합니다. 즉, $m_{\mathcal{H}}(N)<2^k$ 를 만족하는 k를 말합니다. 예를 들어 아까 보았던 2D Perceptron의 경우, $N=3$ 일 때 $m_{\mathcal{H}}(3)=8$이었지만 $N=4$일 때 $m_{\mathcal{H}}(4)=14<16$ 이었으므로 $k=4$가 됩니다.

이 Break Point의 개념이 상당히 중요한데, Break Point $k$ 이후로는 절때 최대의 Dichotomies를 만들 수 없기 때문입니다. (즉, 2D Perceptron을 예로 든다면 4 이상인 모든 $N$에 대하여 $m_{\mathcal{H}}(N)<2^N$이 성립한다는 뜻입니다.)

그럼 아까 예제로 들었던 3가지 예제에서 Break Point를 구해보겠습니다.

Positive Ray의 경우에는 $m_{\mathcal{H}}(N)=N+1<2^N$을 만족하는 최소의 $N$이 2이므로, Break Point $k=2$임을 알 수 있습니다. Positive Interval의 경우도 마찬가지로 $m_{\mathcal{H}}(2)=4, m_{\mathcal{H}}(3)=7<9$ 이므로 $k=3$이 Break Point임을 쉽게 계산할 수 있습니다. 그런데 Convex Set의 경우에는, $m_{\mathcal{H}}(N)=2^N$ 이었으므로, 어떤 $k$에 대해서도 Break Point를 찾을 수 없습니다.

여기서 재밌는 결과를 도출 할 수 있습니다. 만약에 Break Point가 없다면, Growth Function은 $m_{\mathcal{H}}(N)=2^N$이 되지만, Break Point가 존재하기만 한다면 $m_{\mathcal{H}}(N)$는 $N$에 대해서 Polynomial 하다는 것을 알 수 있습니다. 15번 슬라이드에서의 문제가 해결되는 느낌입니다.

Puzzle

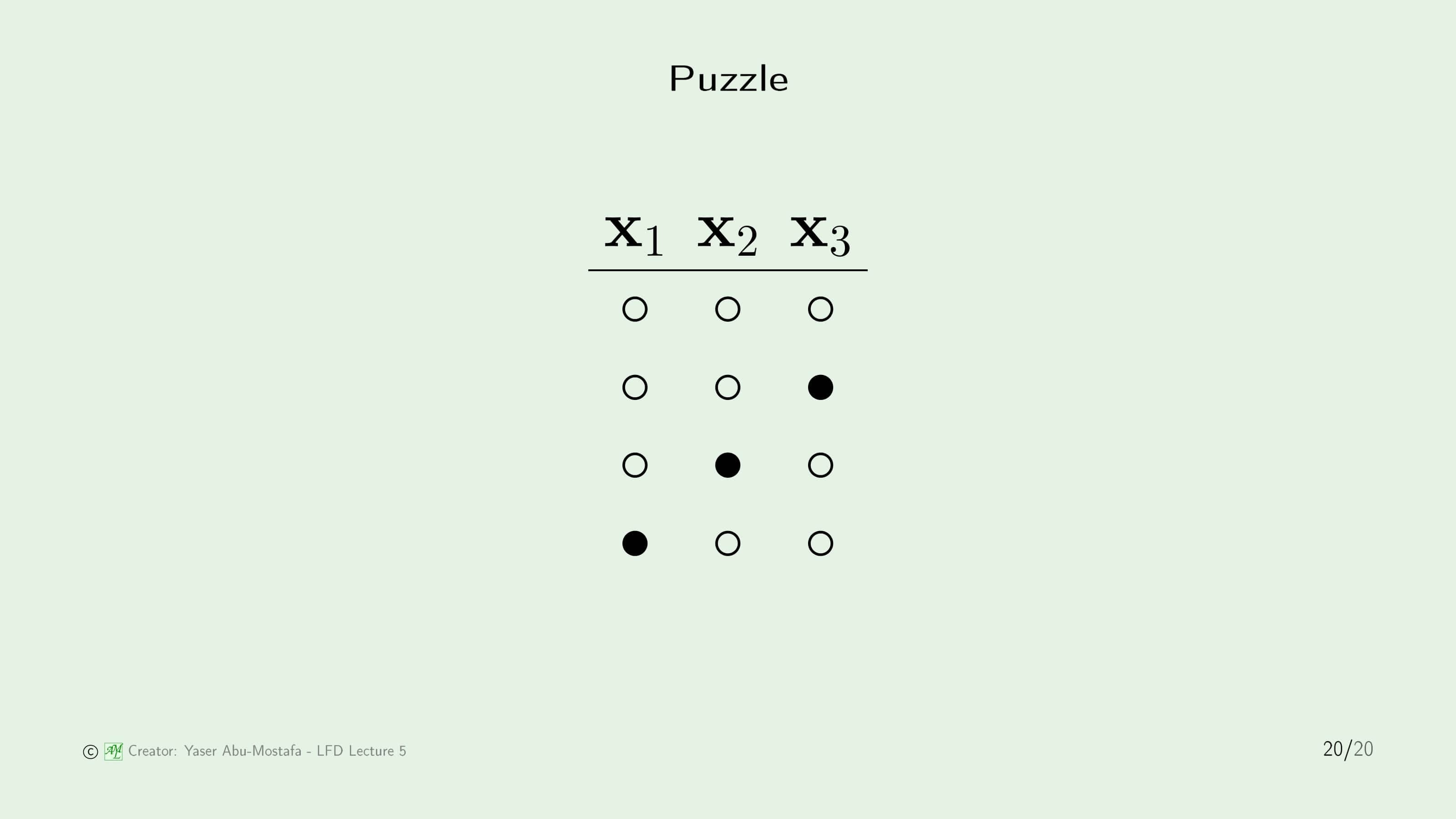
마지막으로 간단한 퍼즐을 하나 풀어봅시다.

사실 이 슬라이드에는 문제를 내기도 전에 정답이 이미 화면에 나와있는데, 원래 문제는 Break Point $k=2$일 때, $N=3$인 경우 가능한 모든 경우의 수를 구하라 입니다. 이를 해결하기 위해 차근차근 한번 생각해봅시다. 경우의 수를 하나하나 따져보면 계산할 수 있습니다.

Break Point가 $k=2$ 이므로, $m_{\mathcal{H}}(1)=2$ 임을 알 수 있습니다. 가장 먼저 모든 점이 -1로 분류되는 상황으로 시작해 봅시다.

자, 이 상황은 일단 아무런 문제가 없습니다. 이제 $\mathbf{x}_3$가 +1이 되는 경우를 추가합니다.

이것은 아무 문제가 없습니다. 왜냐하면 $x_3$이라는 점 하나만 놓고 보았을 때 $N=1$인 경우 $m_{\mathcal{H}}(1)=2$ 라는 조건에 위배되지 않으니까요. (아래 그림 참고)

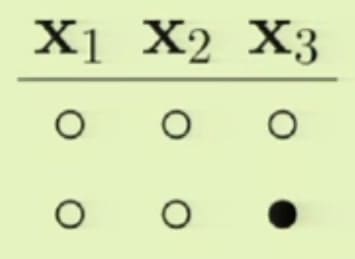
이와 같은 방법으로 $\mathbf{x}_1, \mathbf{x}_2$ 각각에 하나의 점만 +1이 되는 경우를 추가해줍니다. (아래 그림 참고)

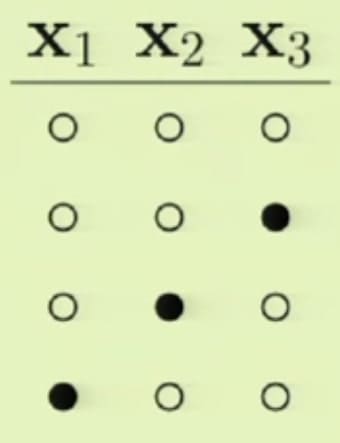
그럼 이제 새로운 경우를 하나 더 추가해보겠습니다. 아래 그림과 같이 $\mathbf{x}_1, \mathbf{x}_3$이 동시에 +1이 되는 상황을 가정해봅시다.

그런데 여기에 문제가 있습니다. 왜 문제가 되는지 여기서 $\mathbf{x}_2$를 지워봅시다.

보시면 첫 번째 경우와 세 번째 경우가 같은 경우이므로 이를 제외하면, 총 4가지의 경우가 나오게 됩니다. 이는 문제에서 제시했던 Break Point가 2라는 조건에 위배됩니다. $m_{\mathcal{H}}(2)<4$이어야 하는데 4개가 나와버렸습니다. 따라서 이 경우는 존재할 수 없다는 것을 알 수 있습니다. 이와 마찬가지로 첫 4가지 경우를 제외하면 어떤 경우도 Break Point가 2라는 조건을 지킬 수 없기 때문에, 정답은 이 4가지 경우만 존재함을 구할 수 있습니다.

제가 쉽게 설명을 못한 것 같은데, 유튜브 강의에서 해당 부분을 확인하시면 훨씬 쉽게 이해하실 수 있을 겁니다.

이번 장은 여기까지입니다. 감사합니다.